2025年中考数学一轮复习 第二章 方程(组)与不等式(组) 第二节 分式方程及其应用 课件(共25张PPT)
文档属性
| 名称 | 2025年中考数学一轮复习 第二章 方程(组)与不等式(组) 第二节 分式方程及其应用 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-12 00:00:00 | ||
图片预览








文档简介
(共25张PPT)
第二章 方程(组)与不等式(组)
第一部分 中考考点梳理
第二节 分式方程及其应用
2025年中考数学一轮复习
考点梳理
1.分式方程的概念及其解法[基础点]
(1)概念:分母中含有①________的方程叫做分式方程.分式方程去分母化
为整式方程时,若该整式方程的根使原分式方程的最简公分母为0,则称该
根是分式方程的增根.
未知数
(2)基本思想:解分式方程的基本思想是转化思想,即把分式方程转化为②
__________求解.
整式方程
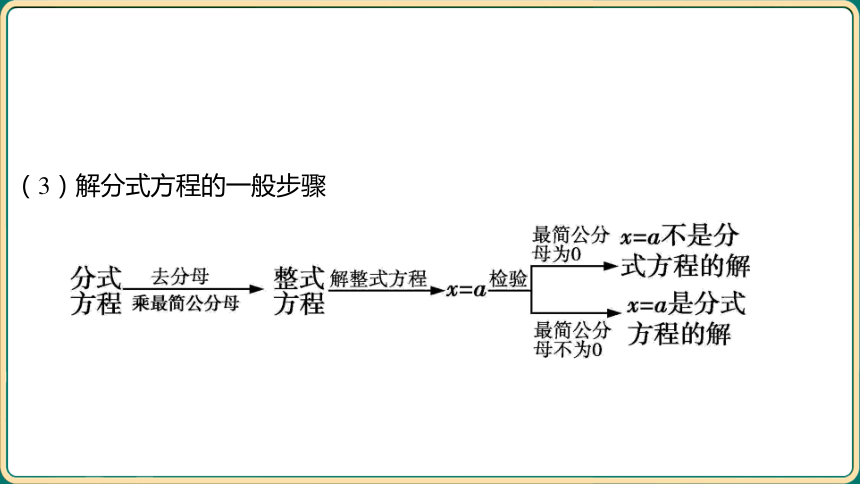
(3)解分式方程的一般步骤
【易失分点】 解分式方程的常见误区
①漏乘不含分母的项:去分母时,要把方程两边的式子作为一个整体,不要漏
乘不含分母的项.
②忘记验根:求出的整式方程的根还要代入分式方程的最简公分母中进行检
验,只有使最简公分母不为零的解才是原方程的解.
③去分母、移项时忽略符号的变化.
例:解分式方程 .
解:方程两边乘 ,
解得 .
不是原分式方程的解, 原分式方程无解.
回练课本
1.解下列分式方程:
(1) ;
[答案] 方程两边乘,得 ,
,
,
解得 ,
检验:当时, .
是原方程的根.
(2) ;
[答案] 方程两边乘,得 ,
,
,
解得 .
检验:当时, ,
原分式方程无解.
(3) .
[答案] 方程两边乘,得 ,
,
,
解得 .
检验:当时, ,
是原分式方程的解.
2.分式方程的应用[重点]
(1)常见类型
【提分指南】 双检验:(1)检验是否为分式方程的解;(2)检验是否满足应
用题的实际意义.
(2)列分式方程解应用题的一般步骤
2.某商厦进货员预测一种应季衬衫能畅销市场,就用8万元购进这种衬衫,面市
后果然供不应求.商厦又用17.6万元购进了第二批这种衬衫,所购数量是第一批
购进量的2倍,但每件衬衫的进价贵了4元.商厦销售这种衬衫时每件定价都是
58元,最后剩下150件按八折销售,很快售完.在这两笔生意中,商厦共赢利
___ _ 元.
90260
回练课本
考法 分式方程的应用
例 在全民健身运动中,骑行运动颇受市民青睐,甲、乙两骑行爱好者约定
从地沿相同路线骑行去距地30千米的 地[1],已知甲骑行的速度是乙的
1.2倍[2].
(1)若乙先骑行2千米,甲才开始从 地出发,则甲出发半小时恰好追上乙
[3],求甲骑行的速度;
. .
. .
. .
. .
[答案] 设乙骑行的速度是千米/时,则甲骑行的速度是 千米/时,
由题意,得 ,
解得 ,
则 .
答:甲骑行的速度是24千米/时.
(2)若乙先骑行20分钟,甲才开始从地出发,则甲、乙恰好同时到达 地
[4],求甲骑行的速度.
[答案] 设乙骑行的速度是千米/时,则甲骑行的速度是 千米/时.
由题意,得 ,
解得 .
经检验, 是原方程的解,且符合题意.
则 .
答:甲骑行的速度为18千米/时.
. .
【解题指导】
由[1]得,两地之间的路程 千米.
由[2]得等量关系:甲骑行的速度 乙骑行的速度.
由[3]得等量关系:甲骑行的速度乙骑行的速度 .
由[4]得等量关系:总路程 甲的速度分钟总路程 乙的速度.
注意:列方程时,等号两边的量的单位要一致.
命题点1 解分式方程[8年1考]
1.[2024福建中考,19] 解方程: .
[答案] 方程两边都乘 ,得
.
解得 .
经检验, 是原方程的根.
命题点2 分式方程的应用[8年1考]
2.[2020福建中考,8] 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯
二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:
现请人代买一批椽,这批椽的价钱为6 210文.如果每株椽的运费是3文,那么少
拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6 210文能买多少株
椽.设这批椽的数量为 株,则符合题意的方程是( )
A
A. B.
C. D.
3.[2023南平质检] 百合花是南平市花.某校为了丰富学生的校园生活,准备购进
黄色和粉色两种百合.其中粉色百合一盆的价格比黄色百合一盆的价格少20元,
用1 200元购进的黄色百合的盆数和用900元购进的粉色百合的盆数相等.
(1)求黄色百合和粉色百合一盆的价格分别是多少;
[答案] 设一盆黄色百合的价格是元,则一盆粉色百合的价格是 元.
依题意,得 ,
解得 ,
经检验, 为原分式方程的解,
.
答:一盆黄色百合的价格是80元,一盆粉色百合的价格是60元.
(2)该校计划用800元购买黄色百合和粉色百合,且两种百合都必须购买,
请问:恰好用完800元的购买方案有哪几种?
[答案] 设黄色百合买盆,粉色百合买 盆,
依题意,得 ,
即 ,
因为, 为正整数,
所以符合条件的解为或或
答:共有三种购买方案,分别是:
①黄色百合购买1盆,粉色百合购买12盆;
②黄色百合购买4盆,粉色百合购买8盆;
③黄色百合购买7盆,粉色百合购买4盆.
4.[2024三明质检] 随着电动汽车的迅猛发展,我国已成为全球最大的电动汽
车市场,在很多高速公路服务区里既有加油站又有充电桩.
(1)在某个服务区,电动汽车的充电桩数量是燃油汽车加油枪数量的1.5倍,统
计发现:在1个小时内,平均每个充电桩可以为2辆电动汽车充电,平均一个加油
枪可以为10辆燃油汽车加油,这样在这1小时内可以为104辆汽车提供充电、加
油服务.那么这个服务区的充电桩和加油枪分别有多少个
[答案] 方法一:设这个服务区的加油枪有个,则充电桩有 个,
根据题意,得 ,
解得,则 .
答:这个服务区的加油枪有8个,充电桩有12个.
方法二:设这个服务区的加油枪有个,充电桩有 个,
根据题意,得
解得
答:这个服务区的加油枪有8个,充电桩有12个.
(2)一般情况下,在高速公路上行驶时电动汽车平均每公里所耗电费比燃油
汽车平均每公里所耗油费少0.6元.若两位车主在服务区分别花60元给电动汽
车充电、花300元给燃油汽车加油,电动汽车可行驶的里程与燃油汽车可行驶
的里程相等,那么电动汽车在高速公路上行驶时平均每公里所耗电费为
多少元
[答案] 设电动汽车在高速公路上行驶时平均每公里所耗电费为 元,
则燃油汽车平均每公里所耗油费为 元,
根据题意,得 ,
解得 ,
经检验, 是原方程的解,且符合题意.
答:电动汽车在高速公路上行驶时平均每公里所耗电费为0.15元.
第二章 方程(组)与不等式(组)
第一部分 中考考点梳理
第二节 分式方程及其应用
2025年中考数学一轮复习
考点梳理
1.分式方程的概念及其解法[基础点]
(1)概念:分母中含有①________的方程叫做分式方程.分式方程去分母化
为整式方程时,若该整式方程的根使原分式方程的最简公分母为0,则称该
根是分式方程的增根.
未知数
(2)基本思想:解分式方程的基本思想是转化思想,即把分式方程转化为②
__________求解.
整式方程
(3)解分式方程的一般步骤
【易失分点】 解分式方程的常见误区
①漏乘不含分母的项:去分母时,要把方程两边的式子作为一个整体,不要漏
乘不含分母的项.
②忘记验根:求出的整式方程的根还要代入分式方程的最简公分母中进行检
验,只有使最简公分母不为零的解才是原方程的解.
③去分母、移项时忽略符号的变化.
例:解分式方程 .
解:方程两边乘 ,
解得 .
不是原分式方程的解, 原分式方程无解.
回练课本
1.解下列分式方程:
(1) ;
[答案] 方程两边乘,得 ,
,
,
解得 ,
检验:当时, .
是原方程的根.
(2) ;
[答案] 方程两边乘,得 ,
,
,
解得 .
检验:当时, ,
原分式方程无解.
(3) .
[答案] 方程两边乘,得 ,
,
,
解得 .
检验:当时, ,
是原分式方程的解.
2.分式方程的应用[重点]
(1)常见类型
【提分指南】 双检验:(1)检验是否为分式方程的解;(2)检验是否满足应
用题的实际意义.
(2)列分式方程解应用题的一般步骤
2.某商厦进货员预测一种应季衬衫能畅销市场,就用8万元购进这种衬衫,面市
后果然供不应求.商厦又用17.6万元购进了第二批这种衬衫,所购数量是第一批
购进量的2倍,但每件衬衫的进价贵了4元.商厦销售这种衬衫时每件定价都是
58元,最后剩下150件按八折销售,很快售完.在这两笔生意中,商厦共赢利
___ _ 元.
90260
回练课本
考法 分式方程的应用
例 在全民健身运动中,骑行运动颇受市民青睐,甲、乙两骑行爱好者约定
从地沿相同路线骑行去距地30千米的 地[1],已知甲骑行的速度是乙的
1.2倍[2].
(1)若乙先骑行2千米,甲才开始从 地出发,则甲出发半小时恰好追上乙
[3],求甲骑行的速度;
. .
. .
. .
. .
[答案] 设乙骑行的速度是千米/时,则甲骑行的速度是 千米/时,
由题意,得 ,
解得 ,
则 .
答:甲骑行的速度是24千米/时.
(2)若乙先骑行20分钟,甲才开始从地出发,则甲、乙恰好同时到达 地
[4],求甲骑行的速度.
[答案] 设乙骑行的速度是千米/时,则甲骑行的速度是 千米/时.
由题意,得 ,
解得 .
经检验, 是原方程的解,且符合题意.
则 .
答:甲骑行的速度为18千米/时.
. .
【解题指导】
由[1]得,两地之间的路程 千米.
由[2]得等量关系:甲骑行的速度 乙骑行的速度.
由[3]得等量关系:甲骑行的速度乙骑行的速度 .
由[4]得等量关系:总路程 甲的速度分钟总路程 乙的速度.
注意:列方程时,等号两边的量的单位要一致.
命题点1 解分式方程[8年1考]
1.[2024福建中考,19] 解方程: .
[答案] 方程两边都乘 ,得
.
解得 .
经检验, 是原方程的根.
命题点2 分式方程的应用[8年1考]
2.[2020福建中考,8] 我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯
二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:
现请人代买一批椽,这批椽的价钱为6 210文.如果每株椽的运费是3文,那么少
拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问6 210文能买多少株
椽.设这批椽的数量为 株,则符合题意的方程是( )
A
A. B.
C. D.
3.[2023南平质检] 百合花是南平市花.某校为了丰富学生的校园生活,准备购进
黄色和粉色两种百合.其中粉色百合一盆的价格比黄色百合一盆的价格少20元,
用1 200元购进的黄色百合的盆数和用900元购进的粉色百合的盆数相等.
(1)求黄色百合和粉色百合一盆的价格分别是多少;
[答案] 设一盆黄色百合的价格是元,则一盆粉色百合的价格是 元.
依题意,得 ,
解得 ,
经检验, 为原分式方程的解,
.
答:一盆黄色百合的价格是80元,一盆粉色百合的价格是60元.
(2)该校计划用800元购买黄色百合和粉色百合,且两种百合都必须购买,
请问:恰好用完800元的购买方案有哪几种?
[答案] 设黄色百合买盆,粉色百合买 盆,
依题意,得 ,
即 ,
因为, 为正整数,
所以符合条件的解为或或
答:共有三种购买方案,分别是:
①黄色百合购买1盆,粉色百合购买12盆;
②黄色百合购买4盆,粉色百合购买8盆;
③黄色百合购买7盆,粉色百合购买4盆.
4.[2024三明质检] 随着电动汽车的迅猛发展,我国已成为全球最大的电动汽
车市场,在很多高速公路服务区里既有加油站又有充电桩.
(1)在某个服务区,电动汽车的充电桩数量是燃油汽车加油枪数量的1.5倍,统
计发现:在1个小时内,平均每个充电桩可以为2辆电动汽车充电,平均一个加油
枪可以为10辆燃油汽车加油,这样在这1小时内可以为104辆汽车提供充电、加
油服务.那么这个服务区的充电桩和加油枪分别有多少个
[答案] 方法一:设这个服务区的加油枪有个,则充电桩有 个,
根据题意,得 ,
解得,则 .
答:这个服务区的加油枪有8个,充电桩有12个.
方法二:设这个服务区的加油枪有个,充电桩有 个,
根据题意,得
解得
答:这个服务区的加油枪有8个,充电桩有12个.
(2)一般情况下,在高速公路上行驶时电动汽车平均每公里所耗电费比燃油
汽车平均每公里所耗油费少0.6元.若两位车主在服务区分别花60元给电动汽
车充电、花300元给燃油汽车加油,电动汽车可行驶的里程与燃油汽车可行驶
的里程相等,那么电动汽车在高速公路上行驶时平均每公里所耗电费为
多少元
[答案] 设电动汽车在高速公路上行驶时平均每公里所耗电费为 元,
则燃油汽车平均每公里所耗油费为 元,
根据题意,得 ,
解得 ,
经检验, 是原方程的解,且符合题意.
答:电动汽车在高速公路上行驶时平均每公里所耗电费为0.15元.
同课章节目录
