2025年中考数学一轮复习 第二章 方程(组)与不等式(组) 第三节 一元二次方程及其应用 课件(共25张PPT)
文档属性
| 名称 | 2025年中考数学一轮复习 第二章 方程(组)与不等式(组) 第三节 一元二次方程及其应用 课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-12 00:00:00 | ||
图片预览






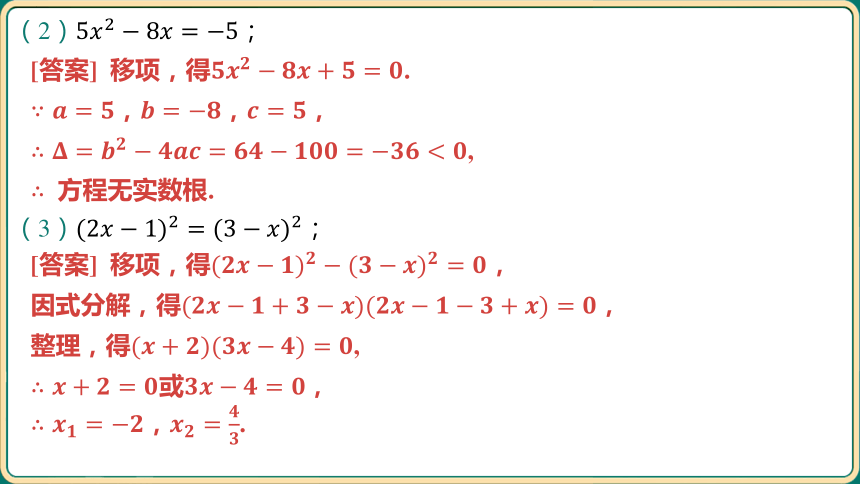


文档简介
(共25张PPT)
第二章 方程(组)与不等式(组)
第一部分 中考考点梳理
第三节 一元二次方程及其应用
2025年中考数学一轮复习
考点梳理
1.一元二次方程[基础点]
定义 只含有一个未知数(一元),并且未知数的最高次数是2(二次)
的整式方程,叫做一元二次方程.
一般形式 (,,为常数,且 ①___0).
解 使方程左右两边相等的未知数的值就是这个一元二次方程的解
(或根).
回练课本
1.(1)将方程 化成一般形式是__________________,
其中二次项系数为___,常数项为____.
(2)若2是关于的方程 的一个根,则这个方程的另一个根是____.
6
2.一元二次方程的解法[基础点]
适用情况 方程的根
直接开平方法 ,
,
配方法 公式法 ( , ②___0) ③_ __________
因式分解法
【易失分点】 解一元二次方程时的注意事项
①用直接开平方法解一元二次方程,开平方时不能将平方根误当作算术平方根,
以免丢根.如方程两边开平方,得,而非 .
②使用公式法时,要先把一元二次方程化为 的形式,代入
公式时注意,, 的符号.
③用因式分解法解一元二次方程时,不能直接约去含未知数的因式,以免丢根.
如:方程的根是或,而非 .解此类方程
时应先移项,再提取公因式求解.
2.用适当的方法解下列方程:
(1) ;
[答案] 移项,得 ,
配方,得 ,
整理,得 .
由此可得 ,
, .
回练课本
(2) ;
[答案] 移项,得 .
,, ,
,
方程无实数根.
(3) ;
[答案] 移项,得 ,
因式分解,得 ,
整理,得 ,
或 ,
, .
(4) .
[答案] 把 看成一个整体,
因式分解,得 ,
整理,得 ,
解得, .
3.一元二次方程根的判别式及根与系数的关系[基础点]
(1)根与判别式的关系
根的判别式:关于的一元二次方程 的根的判别式为
,通常用希腊字母“ ”表示.
方程 的根的情况:
方程 有④____________的实数根.
方程 有⑤__________的实数根.
方程 ⑥______实数根.
两个不相等
两个相等
没有
【易失分点】 因忽视一元二次方程中二次项系数不为0的隐含条件而出错
例:已知关于的一元二次方程有两个实数根,求 的取值
范围.
解:因为该一元二次方程有两个实数根,
解得且,即当且 时,方程有两个实数根.
(2)根与系数的关系(课标变化:由选学内容调整为考查内容)
若,是一元二次方程 的两个根,则
, .
【注意】 应用根与系数关系的前提是方程有解.
【解题通法】 利用根与系数的关系求代数式值的方法
求与一元二次方程的两根有关的代数式的值时,一般利用恒等变形将代数式
转化为含
结合一元二次方程根的定义.几种常用变形如下:
①
②
③ .
④ .
⑤ .
⑥ .
3.(1)已知关于的一元二次方程 ,则下列对该方程的根的
判断,正确的是( )
C
A.没有实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.实数根的个数与 的取值有关
(2)已知关于的一元二次方程 有两个实数根,
则 的取值范围是( )
D
A. B.且 C. D.且
(3)已知,是方程的两根,则 ____.
(4)若,是方程的两个根,则 的值为____.
回练课本
4.一元二次方程的应用[重点]
(1)列一元二次方程解应用题的步骤和列一元一次方程解应用题的步骤相
同,共分审、设、列、解、验、答六步.
(2)一元二次方程的实际应用问题的常见类型
A.增长率型
.增长率增量 基础量 ;
.设为原来的量,为变化后的量,当为平均增长率, 为增长次数时,
;当为平均下降率,为下降次数时, .
B.图形面积型
四边形为矩形,空白部分的图形的宽均为 .
_________________________________ ________________________________ ________________________________ ________________________________
⑦_________ ____________ ⑧_______ ___________ ⑨_______ ___________ ⑩_______
_________
4.(1)已知某部优秀电影第一天票房约为2亿元,前三天票房累计约10亿元.
若每天票房的平均增长率为 ,依题意可列方程为_______________________
_________.
(2)如图,在长为32米、宽为20米的矩形地面上修筑
同样宽的道路(图中阴影部分),余下部分种植草坪,
已知道路的面积为100米,设道路的宽为 米,则可列
方程为______________________.
回练课本
考法 一元二次方程的实际应用
例 某休闲服装店在销售中发现,某款休闲装每件进价为80元,售价为120元,
每天可售出20件[1].经市场调查发现,如果每件该款休闲装降价1元,那么
平均每天可多售出2件[2].
(1)若该服装店三月份的销售量比一月份增长了 [3],求二、三月份销
售量的月平均增长率.
[答案] 设二、三月份销售量的月平均增长率为,一月份的销售量为 .
由题意得 ,
解得, (不合题意,舍去),
答:二、三月份销售量的月平均增长率为 .
. .
. .
. .
. .
. .
(2)若销售该款休闲装平均每天盈利1 200元[4],且要尽快减少库存[5],
则每件应降价多少元
[答案] 设每件该款休闲装降价元,则每件的销售利润为 元,
每天可售出 件.
依题意得 ,
整理得 ,
解得, .
要尽快减少库存, .
答:每件该款休闲装应降价20元.
. .
. .
(3)销售该款休闲装平均每天的盈利有可能达到1 600元[6]吗?请说明理
由.
[答案] 平均每天的盈利不可能达到1 600元,理由如下:
设每件该款休闲装降价元,则每件的销售利润为 元,每天
可售出 件.
依题意得 ,
整理得 .
,
原方程无实数根,
平均每天的盈利不可能达到1 600元.
. .
解题指导
由[1][2]得等量关系:每件的利润 降价的金额;每天的销
售量降价的金额 .
由[3]得等量关系:三月份的销售量一月份的销售量 .
由[4]得等量关系: 每件的利润×每天的销售量.
由[5]可知在满足条件的情况下,销售量的取值越大越好.
结合[6],令每件的利润×每天的销售量 ,再进行判断.
命题点 一元二次方程的实际应用[8年3考]
1.[2024福州质检] 用一条长的绳子围成一个面积为 的矩形,设该
矩形一边长为 ,则下列符合题意的方程是( )
C
A. B.
C. D.
2.[2023福建中考,6] 根据福建省统计局数据,福建省2020年的地区生产总
值为亿元,2022年的地区生产总值为 亿元.设这两年福建
省地区生产总值的年平均增长率为 ,根据题意可列方程( )
B
A. B.
C. D.
3.[2023南平质检] 某市举行篮球联赛,每两支球队之间只进行一场比赛,一
共比赛了45场,设有 支球队参加比赛,可列方程为( )
B
A. B. C. D.
4.[2023漳州质检] 某中学为了提高学生的身体素质,决定在2023年5月举办
“坚持锻炼,活力无限”的健身活动,并准备购买一些体育器材为活动做准
备.经调查,某公司有A,B两种系列的体育器材可供选择,该公司2022年每
套A系列体育器材的售价为2 500元,经过连续两次降价,2023年4月每套A
系列体育器材的售价为1 600元.
(1)求每套A系列体育器材这两次降价的平均下降率 ;
[答案] 依题意,得 ,
解得, (不合题意,舍去).
答:每套A系列体育器材这两次降价的平均下降率为 .
(2)2023年4月该学校经过招标,决定采购该公司A,B两种系列的体育器材
共80套,采购专项经费总计不超过11.2万元,采购合同规定:每套A系列体
育器材售价为1 600元,每套B系列体育器材售价为 元,则A系
列体育器材最多可购买多少套?
[答案] 设A系列体育器材可购买套,则B系列体育器材可购买 套,
依题意,得 ,
解得 .
答:A系列体育器材最多可购买40套.
第二章 方程(组)与不等式(组)
第一部分 中考考点梳理
第三节 一元二次方程及其应用
2025年中考数学一轮复习
考点梳理
1.一元二次方程[基础点]
定义 只含有一个未知数(一元),并且未知数的最高次数是2(二次)
的整式方程,叫做一元二次方程.
一般形式 (,,为常数,且 ①___0).
解 使方程左右两边相等的未知数的值就是这个一元二次方程的解
(或根).
回练课本
1.(1)将方程 化成一般形式是__________________,
其中二次项系数为___,常数项为____.
(2)若2是关于的方程 的一个根,则这个方程的另一个根是____.
6
2.一元二次方程的解法[基础点]
适用情况 方程的根
直接开平方法 ,
,
配方法 公式法 ( , ②___0) ③_ __________
因式分解法
【易失分点】 解一元二次方程时的注意事项
①用直接开平方法解一元二次方程,开平方时不能将平方根误当作算术平方根,
以免丢根.如方程两边开平方,得,而非 .
②使用公式法时,要先把一元二次方程化为 的形式,代入
公式时注意,, 的符号.
③用因式分解法解一元二次方程时,不能直接约去含未知数的因式,以免丢根.
如:方程的根是或,而非 .解此类方程
时应先移项,再提取公因式求解.
2.用适当的方法解下列方程:
(1) ;
[答案] 移项,得 ,
配方,得 ,
整理,得 .
由此可得 ,
, .
回练课本
(2) ;
[答案] 移项,得 .
,, ,
,
方程无实数根.
(3) ;
[答案] 移项,得 ,
因式分解,得 ,
整理,得 ,
或 ,
, .
(4) .
[答案] 把 看成一个整体,
因式分解,得 ,
整理,得 ,
解得, .
3.一元二次方程根的判别式及根与系数的关系[基础点]
(1)根与判别式的关系
根的判别式:关于的一元二次方程 的根的判别式为
,通常用希腊字母“ ”表示.
方程 的根的情况:
方程 有④____________的实数根.
方程 有⑤__________的实数根.
方程 ⑥______实数根.
两个不相等
两个相等
没有
【易失分点】 因忽视一元二次方程中二次项系数不为0的隐含条件而出错
例:已知关于的一元二次方程有两个实数根,求 的取值
范围.
解:因为该一元二次方程有两个实数根,
解得且,即当且 时,方程有两个实数根.
(2)根与系数的关系(课标变化:由选学内容调整为考查内容)
若,是一元二次方程 的两个根,则
, .
【注意】 应用根与系数关系的前提是方程有解.
【解题通法】 利用根与系数的关系求代数式值的方法
求与一元二次方程的两根有关的代数式的值时,一般利用恒等变形将代数式
转化为含
结合一元二次方程根的定义.几种常用变形如下:
①
②
③ .
④ .
⑤ .
⑥ .
3.(1)已知关于的一元二次方程 ,则下列对该方程的根的
判断,正确的是( )
C
A.没有实数根 B.有两个相等的实数根
C.有两个不相等的实数根 D.实数根的个数与 的取值有关
(2)已知关于的一元二次方程 有两个实数根,
则 的取值范围是( )
D
A. B.且 C. D.且
(3)已知,是方程的两根,则 ____.
(4)若,是方程的两个根,则 的值为____.
回练课本
4.一元二次方程的应用[重点]
(1)列一元二次方程解应用题的步骤和列一元一次方程解应用题的步骤相
同,共分审、设、列、解、验、答六步.
(2)一元二次方程的实际应用问题的常见类型
A.增长率型
.增长率增量 基础量 ;
.设为原来的量,为变化后的量,当为平均增长率, 为增长次数时,
;当为平均下降率,为下降次数时, .
B.图形面积型
四边形为矩形,空白部分的图形的宽均为 .
_________________________________ ________________________________ ________________________________ ________________________________
⑦_________ ____________ ⑧_______ ___________ ⑨_______ ___________ ⑩_______
_________
4.(1)已知某部优秀电影第一天票房约为2亿元,前三天票房累计约10亿元.
若每天票房的平均增长率为 ,依题意可列方程为_______________________
_________.
(2)如图,在长为32米、宽为20米的矩形地面上修筑
同样宽的道路(图中阴影部分),余下部分种植草坪,
已知道路的面积为100米,设道路的宽为 米,则可列
方程为______________________.
回练课本
考法 一元二次方程的实际应用
例 某休闲服装店在销售中发现,某款休闲装每件进价为80元,售价为120元,
每天可售出20件[1].经市场调查发现,如果每件该款休闲装降价1元,那么
平均每天可多售出2件[2].
(1)若该服装店三月份的销售量比一月份增长了 [3],求二、三月份销
售量的月平均增长率.
[答案] 设二、三月份销售量的月平均增长率为,一月份的销售量为 .
由题意得 ,
解得, (不合题意,舍去),
答:二、三月份销售量的月平均增长率为 .
. .
. .
. .
. .
. .
(2)若销售该款休闲装平均每天盈利1 200元[4],且要尽快减少库存[5],
则每件应降价多少元
[答案] 设每件该款休闲装降价元,则每件的销售利润为 元,
每天可售出 件.
依题意得 ,
整理得 ,
解得, .
要尽快减少库存, .
答:每件该款休闲装应降价20元.
. .
. .
(3)销售该款休闲装平均每天的盈利有可能达到1 600元[6]吗?请说明理
由.
[答案] 平均每天的盈利不可能达到1 600元,理由如下:
设每件该款休闲装降价元,则每件的销售利润为 元,每天
可售出 件.
依题意得 ,
整理得 .
,
原方程无实数根,
平均每天的盈利不可能达到1 600元.
. .
解题指导
由[1][2]得等量关系:每件的利润 降价的金额;每天的销
售量降价的金额 .
由[3]得等量关系:三月份的销售量一月份的销售量 .
由[4]得等量关系: 每件的利润×每天的销售量.
由[5]可知在满足条件的情况下,销售量的取值越大越好.
结合[6],令每件的利润×每天的销售量 ,再进行判断.
命题点 一元二次方程的实际应用[8年3考]
1.[2024福州质检] 用一条长的绳子围成一个面积为 的矩形,设该
矩形一边长为 ,则下列符合题意的方程是( )
C
A. B.
C. D.
2.[2023福建中考,6] 根据福建省统计局数据,福建省2020年的地区生产总
值为亿元,2022年的地区生产总值为 亿元.设这两年福建
省地区生产总值的年平均增长率为 ,根据题意可列方程( )
B
A. B.
C. D.
3.[2023南平质检] 某市举行篮球联赛,每两支球队之间只进行一场比赛,一
共比赛了45场,设有 支球队参加比赛,可列方程为( )
B
A. B. C. D.
4.[2023漳州质检] 某中学为了提高学生的身体素质,决定在2023年5月举办
“坚持锻炼,活力无限”的健身活动,并准备购买一些体育器材为活动做准
备.经调查,某公司有A,B两种系列的体育器材可供选择,该公司2022年每
套A系列体育器材的售价为2 500元,经过连续两次降价,2023年4月每套A
系列体育器材的售价为1 600元.
(1)求每套A系列体育器材这两次降价的平均下降率 ;
[答案] 依题意,得 ,
解得, (不合题意,舍去).
答:每套A系列体育器材这两次降价的平均下降率为 .
(2)2023年4月该学校经过招标,决定采购该公司A,B两种系列的体育器材
共80套,采购专项经费总计不超过11.2万元,采购合同规定:每套A系列体
育器材售价为1 600元,每套B系列体育器材售价为 元,则A系
列体育器材最多可购买多少套?
[答案] 设A系列体育器材可购买套,则B系列体育器材可购买 套,
依题意,得 ,
解得 .
答:A系列体育器材最多可购买40套.
同课章节目录
