2025年中考数学一轮复习 第二章 方程(组)与不等式(组) 第四节 一次不等式(组)及其应用 课件(共30张PPT)
文档属性
| 名称 | 2025年中考数学一轮复习 第二章 方程(组)与不等式(组) 第四节 一次不等式(组)及其应用 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-12 12:56:55 | ||
图片预览









文档简介
(共30张PPT)
第二章 方程(组)与不等式(组)
第一部分 中考考点梳理
第四节 一次不等式(组)及其应用
2025年中考数学一轮复习
考点梳理
1.不等式的基本性质[基础点]
性质 文字叙述 字母表示
性质1 不等式两边加(或减)同一个数 (或式子),不等号的方向①______. 如果 ,那么
,
.
性质2 不等式两边乘(或除以)同一个正 数,不等号的方向②______. 如果, ,那么
, .
性质3 不等式两边乘(或除以)同一个负 数,不等号的方向③______. 如果, ,那么
, .
不变
不变
改变
回练课本
1.已知 ,则下列不等式成立的是( )
D
A. B. C. D.
(2)解一元一次不等式的一般步骤
【注意】 系数化为1时,乘或除以同一个负数,不等号的方向改变.
2.一元一次不等式及其解法[基础点]
(1)定义:只含有④______未知数,且未知数的次数是⑤___的不等式,叫
做一元一次不等式.
注:一元一次不等式的解有无数个,解集通常表示为或 .
一个
1
2.解不等式 .
[答案] 去分母,得 .
移项、合并同类项,得 ,
两边都除以,得 .
回练课本
3.一元一次不等式组及其解法[重点]
(1)定义:关于同一未知数的几个一元一次不等式合在一起,就组成一个一
元一次不等式组.
(2)解不等式组的一般步骤
先分别解出每个一元一次不等式,再求出它们解集的公共部分,即为不等式
组的解集.
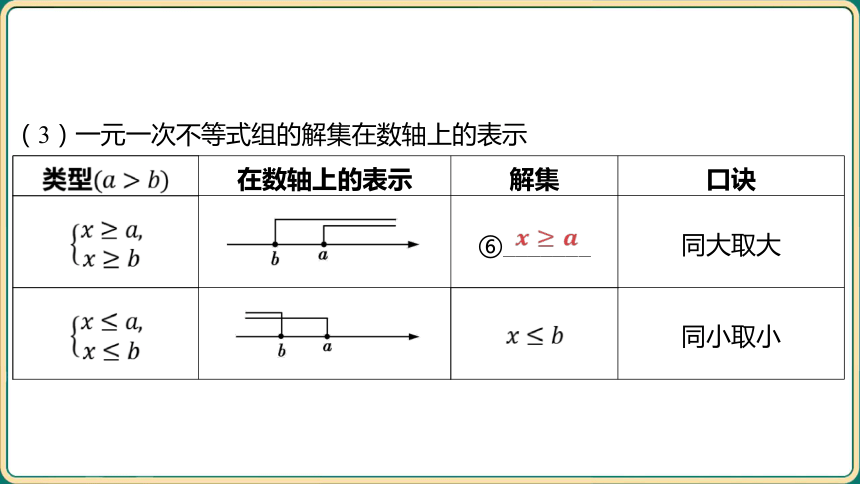
(3)一元一次不等式组的解集在数轴上的表示
类型 在数轴上的表示 解集 口诀
_____________________________________________________ ⑥_______ 同大取大
___________________________________________________ 同小取小
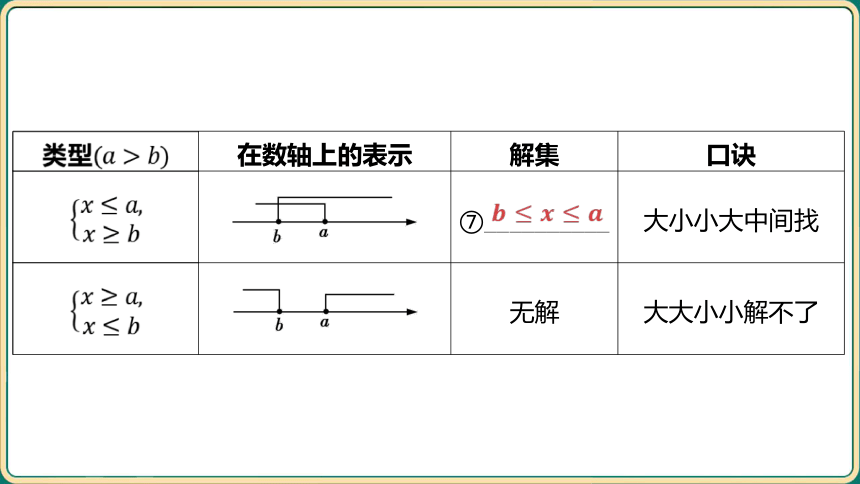
类型 在数轴上的表示 解集 口诀
___________________________________________________ ⑦__________ 大小小大中间找
___________________________________________________ 无解 大大小小解不了
3.解不等式组 并把它的解集在如图所示的数轴上表示出
来.
[答案] 解,得 ,
解,得 ,
原不等式组的解集为 .
将其解集在数轴上表示如下.
回练课本
4.一元一次不等式的应用[重点]
(1)一般步骤
【注意】 检验不等式的解集是否合理,是否符合实际情况.
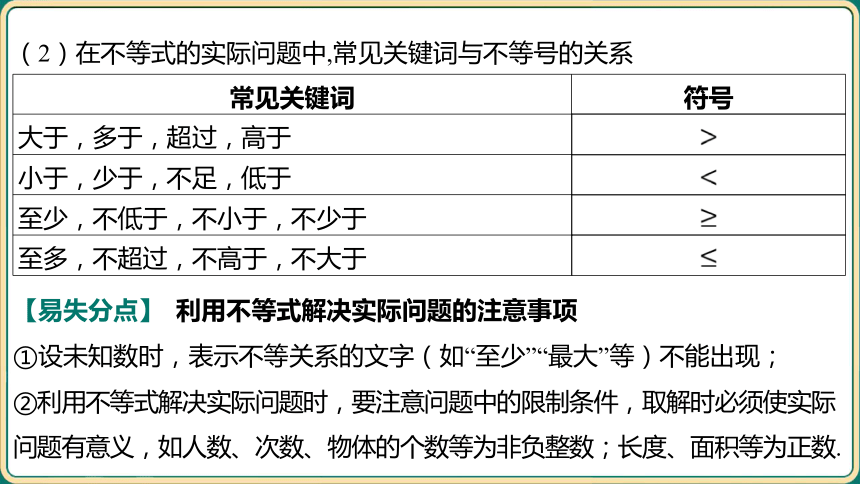
(2)在不等式的实际问题中,常见关键词与不等号的关系
常见关键词 符号
大于,多于,超过,高于
小于,少于,不足,低于
至少,不低于,不小于,不少于
至多,不超过,不高于,不大于
【易失分点】 利用不等式解决实际问题的注意事项
①设未知数时,表示不等关系的文字(如“至少”“最大”等)不能出现;
②利用不等式解决实际问题时,要注意问题中的限制条件,取解时必须使实际
问题有意义,如人数、次数、物体的个数等为非负整数;长度、面积等为正数.
4.(1)根据“与4的和不小于 的3倍”可列不等式:___________.
(2)小明准备用23元购买圆珠笔和铅笔共20支(每种笔至少买一支),已
知每支圆珠笔2元,每支铅笔1元,则小明最多可以买几支圆珠笔?设小明买
了 支圆珠笔,则可列不等式:_________________.
(3)小红读一本400页的书,计划10天内读完,前5天因种种原因只读了100
页,若从第6天起,每天读相同的页数,为了按计划读完,每天至少要读多
少页?设____________________,则可列不等式:________________.
从第6天起每天读页
回练课本
考法 一元一次不等式的实际应用
例 今年五一小长假期间,D市迎来了一个短期旅游高峰.某热门景点的门票
价格如下表:
票的种类 A B C
购票人数 101及以上
票价/(元/人) 50 45 40
某旅行社接待的甲、乙两个旅游团共102人(甲团人数多于乙团 ).在
打算购买门票时,如果把两个团联合作为一个团体购票会比两个团分别购票
节省730元 .
. .
. .
. .
. .
(1)求两个旅游团各有多少人.
[答案] 设甲旅游团有人,乙旅游团有 人.
甲、乙两个旅游团共102人,且甲团人数多于乙团,
甲旅游团的人数在范围内,乙旅游团的人数在 范围内.
根据题意得
解得
答:甲旅游团有58人,乙旅游团有44人.
(2)一个不足50人的旅游团,当游客人数最少为多少人时,购买B种门票比
购买A种门票更省钱 ?
[答案] 设游客人数为人, ,
根据题意得 ,
解得 .
又 为正整数,
的最小值为46.
答:当游客人数最少为46人时,购买B种门票比购买A种门票更省钱.
. .
. .
解题指导
由得等量关系:甲旅游团的人数乙旅游团的人数 .
由 得甲、乙旅游团的人数的取值范围.
由得等量关系:甲旅游团的人数×对应票价 乙旅游团的人数×对应票价
.
由可列出不等式:游客人数 .
提分特训
[2024成都中考] 推进中国式现代化,必须坚持不懈夯实农业基础,推进乡村全
面振兴.某合作社着力发展乡村水果网络销售,在水果收获的季节,该合作社用
17 500元从农户处购进A,B两种水果共 进行销售,其中A种水果收购
价格为10元/,B种水果收购价格为15元/ .
(1)求A,B两种水果各购进多少千克;
[答案] 设A种水果购进,B种水果购进 ,
根据题意,得
解得
答:A种水果购进,B种水果购进 .
(2)已知A种水果运输和仓储过程中质量损失 ,若合作社计划A种水果至
少要获得 的利润,不计其他费用,求A种水果的最低销售单价.
[答案] 设A种水果的销售单价为元/ ,
根据题意,得 ,
解得 .
答:A种水果的最低销售单价为12.5元/ .
命题点1 一元一次不等式(组)的解法[8年7考]
1.[2022福建中考,6] 不等式组 的解集是( )
C
A. B. C. D.
2.[2024福建中考,12] 不等式 的解集是______.
3.[2024三明质检] 解不等式 ,并把它的解集表示在数轴上.
[答案] ,
,
,
,
.
原不等式的解集在数轴上表示如下.
4.[2023福建中考,18] 解不等式组:
[答案] 解不等式①,得 ,
解不等式②,得 ,
所以原不等式组的解集为 .
命题点2 一元一次不等式的实际应用[8年2考]
5.[2024宁德质检] 为丰富校园生活,某校九年级开展篮球比赛活动.比赛得
分规则:在3分线外投篮,投中一球可得3分;在3分线内(含3分线)投篮,
投中一球可得2分;罚球投中一球可得1分.
(1)A班球队在某场比赛中,上半场共投中12个球,其中投中5个2分球,所
得总分为23分,问:该球队上半场比赛罚球得分是多少?
[答案] 设该球队上半场比赛罚球得分是分,则3分球得分为 分.
根据题意,得 ,
解得 .
答:该球队上半场比赛罚球得分是4分.
(2)A班球队预想在下半场比赛中投中12个球,若在没有罚球的情况下,下
半场所得总分不少于29分,则该班级下半场比赛中至少要投中多少个3分球?
[答案] 设该班级下半场比赛中要投中个3分球,则投中 个2分球.
根据题意,得 ,
解得 .
答:该班级下半场比赛中至少要投中5个3分球.
新课标 新考向
【新课标·应用意识】根据以下素材,探索完成任务.
如何设计奖品购买及兑换方案 素材1 某文具店销售某种钢笔与笔记本,已知钢笔的单价是笔记本的2倍,
用120元购买笔记本的数量比用160元购买钢笔的数量多8个.
素材2 某学校花费400元购买该文具店的钢笔和笔记本作为奖品颁发给优秀
学生,两种奖品的购买数量均不少于20个,且购买笔记本的数量是
10的倍数.
素材3 学校花费400元后,文具店赠 送 张兑换券 (如图)用于商品兑换.兑 换后,笔记本与钢笔数量相 同. ______________________________________________________________________________
问题解决 任务1 求商品单价
请运用适当方法,求出钢笔与笔记本的单价.
[答案] 设笔记本的单价为元,则钢笔的单价为 元.
根据题意,得 ,
解得 ,
经检验, 是原方程的根,
.
答:笔记本的单价为5元,钢笔的单价为10元.
任务2 探究购买方案
探究购买钢笔和笔记本数量的所有方案.
[答案] 设购买钢笔支,笔记本 本.
根据题意,得,化简得 ,
,,且 是10的倍数,
或
答:共有三种方案.方案一:购买钢笔30支,笔记本20本;方案二:购买钢笔
25支,笔记本30本;方案三:购买钢笔20支,笔记本40本.
任务3 确定兑换方式
运用数学知识,确定一种符合条件的兑换方式.
[答案] 当购买钢笔30支,笔记本20本时,若文具店赠送8张兑换券,其中2张
兑换钢笔,6张兑换笔记本.(答案不唯一)
解法提示:当购买钢笔30支,笔记本20本时,设张兑换券中有 张兑换券
兑换钢笔.
根据题意,得,整理得 ,
,,均为整数,或
若文具店赠送5张兑换券,5张都兑换成笔记本;若文具店赠送8张兑换券,
则其中2张兑换钢笔,6张兑换笔记本.
第二章 方程(组)与不等式(组)
第一部分 中考考点梳理
第四节 一次不等式(组)及其应用
2025年中考数学一轮复习
考点梳理
1.不等式的基本性质[基础点]
性质 文字叙述 字母表示
性质1 不等式两边加(或减)同一个数 (或式子),不等号的方向①______. 如果 ,那么
,
.
性质2 不等式两边乘(或除以)同一个正 数,不等号的方向②______. 如果, ,那么
, .
性质3 不等式两边乘(或除以)同一个负 数,不等号的方向③______. 如果, ,那么
, .
不变
不变
改变
回练课本
1.已知 ,则下列不等式成立的是( )
D
A. B. C. D.
(2)解一元一次不等式的一般步骤
【注意】 系数化为1时,乘或除以同一个负数,不等号的方向改变.
2.一元一次不等式及其解法[基础点]
(1)定义:只含有④______未知数,且未知数的次数是⑤___的不等式,叫
做一元一次不等式.
注:一元一次不等式的解有无数个,解集通常表示为或 .
一个
1
2.解不等式 .
[答案] 去分母,得 .
移项、合并同类项,得 ,
两边都除以,得 .
回练课本
3.一元一次不等式组及其解法[重点]
(1)定义:关于同一未知数的几个一元一次不等式合在一起,就组成一个一
元一次不等式组.
(2)解不等式组的一般步骤
先分别解出每个一元一次不等式,再求出它们解集的公共部分,即为不等式
组的解集.
(3)一元一次不等式组的解集在数轴上的表示
类型 在数轴上的表示 解集 口诀
_____________________________________________________ ⑥_______ 同大取大
___________________________________________________ 同小取小
类型 在数轴上的表示 解集 口诀
___________________________________________________ ⑦__________ 大小小大中间找
___________________________________________________ 无解 大大小小解不了
3.解不等式组 并把它的解集在如图所示的数轴上表示出
来.
[答案] 解,得 ,
解,得 ,
原不等式组的解集为 .
将其解集在数轴上表示如下.
回练课本
4.一元一次不等式的应用[重点]
(1)一般步骤
【注意】 检验不等式的解集是否合理,是否符合实际情况.
(2)在不等式的实际问题中,常见关键词与不等号的关系
常见关键词 符号
大于,多于,超过,高于
小于,少于,不足,低于
至少,不低于,不小于,不少于
至多,不超过,不高于,不大于
【易失分点】 利用不等式解决实际问题的注意事项
①设未知数时,表示不等关系的文字(如“至少”“最大”等)不能出现;
②利用不等式解决实际问题时,要注意问题中的限制条件,取解时必须使实际
问题有意义,如人数、次数、物体的个数等为非负整数;长度、面积等为正数.
4.(1)根据“与4的和不小于 的3倍”可列不等式:___________.
(2)小明准备用23元购买圆珠笔和铅笔共20支(每种笔至少买一支),已
知每支圆珠笔2元,每支铅笔1元,则小明最多可以买几支圆珠笔?设小明买
了 支圆珠笔,则可列不等式:_________________.
(3)小红读一本400页的书,计划10天内读完,前5天因种种原因只读了100
页,若从第6天起,每天读相同的页数,为了按计划读完,每天至少要读多
少页?设____________________,则可列不等式:________________.
从第6天起每天读页
回练课本
考法 一元一次不等式的实际应用
例 今年五一小长假期间,D市迎来了一个短期旅游高峰.某热门景点的门票
价格如下表:
票的种类 A B C
购票人数 101及以上
票价/(元/人) 50 45 40
某旅行社接待的甲、乙两个旅游团共102人(甲团人数多于乙团 ).在
打算购买门票时,如果把两个团联合作为一个团体购票会比两个团分别购票
节省730元 .
. .
. .
. .
. .
(1)求两个旅游团各有多少人.
[答案] 设甲旅游团有人,乙旅游团有 人.
甲、乙两个旅游团共102人,且甲团人数多于乙团,
甲旅游团的人数在范围内,乙旅游团的人数在 范围内.
根据题意得
解得
答:甲旅游团有58人,乙旅游团有44人.
(2)一个不足50人的旅游团,当游客人数最少为多少人时,购买B种门票比
购买A种门票更省钱 ?
[答案] 设游客人数为人, ,
根据题意得 ,
解得 .
又 为正整数,
的最小值为46.
答:当游客人数最少为46人时,购买B种门票比购买A种门票更省钱.
. .
. .
解题指导
由得等量关系:甲旅游团的人数乙旅游团的人数 .
由 得甲、乙旅游团的人数的取值范围.
由得等量关系:甲旅游团的人数×对应票价 乙旅游团的人数×对应票价
.
由可列出不等式:游客人数 .
提分特训
[2024成都中考] 推进中国式现代化,必须坚持不懈夯实农业基础,推进乡村全
面振兴.某合作社着力发展乡村水果网络销售,在水果收获的季节,该合作社用
17 500元从农户处购进A,B两种水果共 进行销售,其中A种水果收购
价格为10元/,B种水果收购价格为15元/ .
(1)求A,B两种水果各购进多少千克;
[答案] 设A种水果购进,B种水果购进 ,
根据题意,得
解得
答:A种水果购进,B种水果购进 .
(2)已知A种水果运输和仓储过程中质量损失 ,若合作社计划A种水果至
少要获得 的利润,不计其他费用,求A种水果的最低销售单价.
[答案] 设A种水果的销售单价为元/ ,
根据题意,得 ,
解得 .
答:A种水果的最低销售单价为12.5元/ .
命题点1 一元一次不等式(组)的解法[8年7考]
1.[2022福建中考,6] 不等式组 的解集是( )
C
A. B. C. D.
2.[2024福建中考,12] 不等式 的解集是______.
3.[2024三明质检] 解不等式 ,并把它的解集表示在数轴上.
[答案] ,
,
,
,
.
原不等式的解集在数轴上表示如下.
4.[2023福建中考,18] 解不等式组:
[答案] 解不等式①,得 ,
解不等式②,得 ,
所以原不等式组的解集为 .
命题点2 一元一次不等式的实际应用[8年2考]
5.[2024宁德质检] 为丰富校园生活,某校九年级开展篮球比赛活动.比赛得
分规则:在3分线外投篮,投中一球可得3分;在3分线内(含3分线)投篮,
投中一球可得2分;罚球投中一球可得1分.
(1)A班球队在某场比赛中,上半场共投中12个球,其中投中5个2分球,所
得总分为23分,问:该球队上半场比赛罚球得分是多少?
[答案] 设该球队上半场比赛罚球得分是分,则3分球得分为 分.
根据题意,得 ,
解得 .
答:该球队上半场比赛罚球得分是4分.
(2)A班球队预想在下半场比赛中投中12个球,若在没有罚球的情况下,下
半场所得总分不少于29分,则该班级下半场比赛中至少要投中多少个3分球?
[答案] 设该班级下半场比赛中要投中个3分球,则投中 个2分球.
根据题意,得 ,
解得 .
答:该班级下半场比赛中至少要投中5个3分球.
新课标 新考向
【新课标·应用意识】根据以下素材,探索完成任务.
如何设计奖品购买及兑换方案 素材1 某文具店销售某种钢笔与笔记本,已知钢笔的单价是笔记本的2倍,
用120元购买笔记本的数量比用160元购买钢笔的数量多8个.
素材2 某学校花费400元购买该文具店的钢笔和笔记本作为奖品颁发给优秀
学生,两种奖品的购买数量均不少于20个,且购买笔记本的数量是
10的倍数.
素材3 学校花费400元后,文具店赠 送 张兑换券 (如图)用于商品兑换.兑 换后,笔记本与钢笔数量相 同. ______________________________________________________________________________
问题解决 任务1 求商品单价
请运用适当方法,求出钢笔与笔记本的单价.
[答案] 设笔记本的单价为元,则钢笔的单价为 元.
根据题意,得 ,
解得 ,
经检验, 是原方程的根,
.
答:笔记本的单价为5元,钢笔的单价为10元.
任务2 探究购买方案
探究购买钢笔和笔记本数量的所有方案.
[答案] 设购买钢笔支,笔记本 本.
根据题意,得,化简得 ,
,,且 是10的倍数,
或
答:共有三种方案.方案一:购买钢笔30支,笔记本20本;方案二:购买钢笔
25支,笔记本30本;方案三:购买钢笔20支,笔记本40本.
任务3 确定兑换方式
运用数学知识,确定一种符合条件的兑换方式.
[答案] 当购买钢笔30支,笔记本20本时,若文具店赠送8张兑换券,其中2张
兑换钢笔,6张兑换笔记本.(答案不唯一)
解法提示:当购买钢笔30支,笔记本20本时,设张兑换券中有 张兑换券
兑换钢笔.
根据题意,得,整理得 ,
,,均为整数,或
若文具店赠送5张兑换券,5张都兑换成笔记本;若文具店赠送8张兑换券,
则其中2张兑换钢笔,6张兑换笔记本.
同课章节目录
