2025年中考数学一轮复习 -第三章 函数-第一节 平面直角坐标系与函数 课件（共24张PPT）

(共24张PPT)
第三章 函数
第一部分 中考考点梳理
第一节 平面直角坐标系与函数
2025年中考数学一轮复习
考点梳理
1.平面直角坐标系中各象限内点的坐标特征［基础点］
回练课本
1.已知点 .
（1）若，则点 在____________ 象限.
（2）若，则点 在____________象限.
（3）若，则点 在______________.
第一或第三
第二或第四
轴上或轴上
2.特殊位置上点的坐标特征［基础点］
坐标轴上点的坐标特征 轴上点的纵坐标为①___；
轴上点的横坐标为②___；
原点的坐标为③______.
0
0
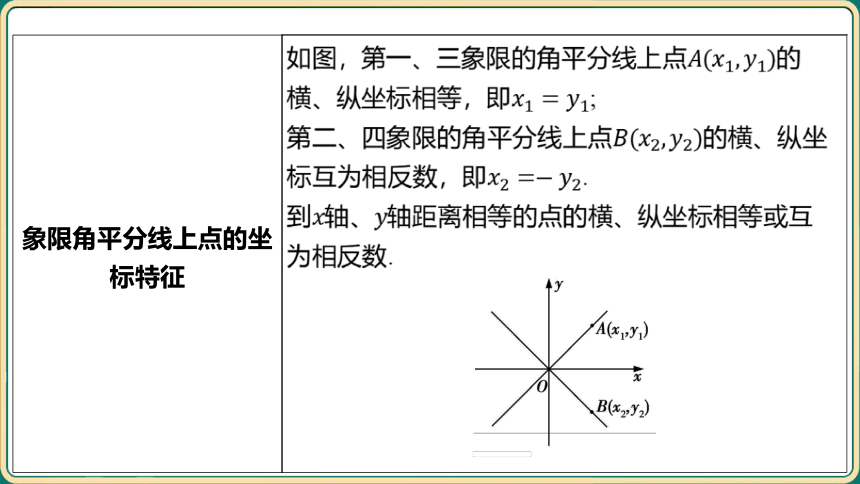
象限角平分线上点的坐 标特征 如图，第一、三象限的角平分线上点 的
横、纵坐标相等，即 ;
第二、四象限的角平分线上点 的横、纵坐
标互为相反数，即 .
到轴、 轴距离相等的点的横、纵坐标相等或互
为相反数.
______________________________________________
到坐标轴距离相等的点 的坐标特征 到 轴距离相等的点的纵坐标的绝对值④______；
到 轴距离相等的点的横坐标的绝对值⑤______.
与坐标轴平行的直线上 点的坐标特征 与 轴平行的直线上点的⑥____坐标相同；
与 轴平行的直线上点的⑦____坐标相同.
相等
相等
纵
横
2.在平面直角坐标系中,点 ,点 .
（1）当时,点 在___轴上;
（2）当时,点 在___轴上;
（3）若点在第一、三象限的角平分线上,则 ____;
（4）若点到轴、轴距离相等,则 ____；
（5）已知轴,且,则_______， ____.
或6
回练课本
【拓展】 点关于直线对称的点的坐标为,点 关于直
线对称的点的坐标为 .
3.与点关于轴对称的点的坐标是______;关于原点对称的点 的坐
标是________；点与点 关于_____对称.
轴
3.点对称的坐标特征［基础点］
回练课本
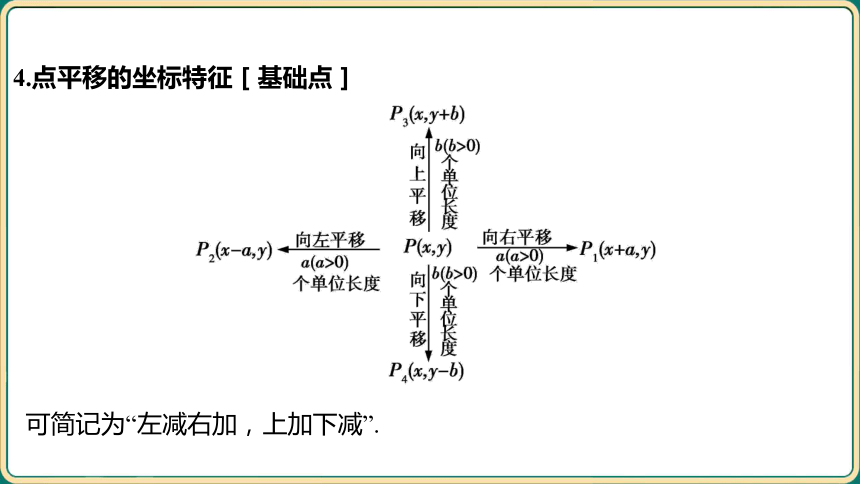
4.点平移的坐标特征［基础点］
可简记为“左减右加，上加下减”.
4.点与点关于轴对称，与点关于原点对称,则点 可以看作是由点
向____平移___个单位长度得到的.
上
8
回练课本
5.用坐标表示位置［基础点］
（1）建立平面直角坐标系:选择一个适当的参照点为原点,确定轴、轴的正
方向;
（2）根据具体问题确定单位长度;
（3）在平面直角坐标系中画出点,写出点的坐标.
5.“凌波仙子生尘袜,水上轻盈步微月.”宋朝诗人黄庭坚以水中仙女借喻水仙花.
如图,将水仙花图置于正方形网格中,点,,均在格点上.若点, ,
则点 的坐标为______.
回练课本
6.点到坐标轴的距离［基础点］
如图,点到轴的距离是,到轴的距离是.
6.在平面直角坐标系的第四象限内有一点,到轴的距离为4,到 轴的距离为5,
则点 的坐标为( )
D
A. B. C. D.
回练课本
7.平面直角坐标系内两点间的距离［基础点］
由勾股定理可知平面直角坐标系内任意两点,之间的距离是
.
特别地：（1）在轴或与轴平行的直线上的两点,之间的距
离为;
（2）在轴或与轴平行的直线上的两点,之间的距离为
;
（3）点到原点的距离是.
7.如图，矩形四个顶点的坐标分别是，， ，
，则的长为___；的长为____；对角线 的长为_____.
3
回练课本
8.函数的有关概念［基础点］
（1）函数的概念
一般地,在一个变化过程中,如果有两个变量与,并且对于的每一个确定的
值,都有唯一确定的值与其对应,那么我们就说是自变量,是的函数.
课标新增：理解函数值的意义.
（2）自变量的取值范围
类型 自变量的取值范围
整式型 全体实数
分式型 分母不等于0
二次根式型 被开方数是非负数
实际问题 要符合实际意义
（3）函数的三种表示方法:列表法、解析式法、图象法.
（4）函数图象的画法:列表、描点、连线.
8.如图是平面直角坐标系中的两条曲线.
（1）能表示是 的函数的是___
（填序号），其中自变量 的取值范围是
______________，函数的最大值为___.
A
3
（2）对（1）中能表示是 的函数的图
象，请你用实际生活中的例子进行说明.
[答案] 答案不唯一，如：小王开车去离家3千米的超市买水果，10分钟后回
到家，图象表示他离家的路程与时间 的函数关系.
回练课本
命题点 平面直角坐标系中点的坐标特征
1.[2024晋江质检] 在平面直角坐标系中，已知点与点 ，
下列说法正确的是( )
A
A.轴 B.轴 C. D.
2.[2024莆田城厢区质检] 在平面直角坐标系中，点， ，当线
段最短时， 的长为( )
C
A.2 B.3 C.4 D.5
3.[2024厦门思明区质检] 已知点，轴，且 ，则点
的坐标是( )
C
A. B.
C.或 D.或
4.[2024漳平质检] 若点 在第二、四象限的角平分线上，则
____．
5.[2024福州长乐区质检] 在平面直角坐标系中，已知点 ，
则线段 长的最小值为____．
新课标 新考向
【新考向·阅读理解】阅读理解：在平面直
角坐标系中，已知点
，，如何求 两点间的距离？如图，在 中，
所以 ．根据上
面得到的公式，解决下列问题：
（1）已知点，试求 两点间的距离；
[答案] 根据两点间的距离公式，得
.
（2）已知点，且，求 的值；
[答案] ，
，
， .
（3）求代数式 的最小值．
[答案] 将看成点到点 和
的距离之和，
的最小值为点到点 和
的距离之和的最小值.
分析可知，当点在以点和为端点的线段上时，点 到
点和的距离之和最小，其最小值为以和 为端点
的线段长度，
的最小值为
．