2025年中考数学一轮复习 -第三章 函数-第二节 一次函数的图象与性质 课件(共23张PPT)
文档属性
| 名称 | 2025年中考数学一轮复习 -第三章 函数-第二节 一次函数的图象与性质 课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-12 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
第三章 函数
第一部分 中考考点梳理
第二节 一次函数的图象与性质
2025年中考数学一轮复习
考点梳理
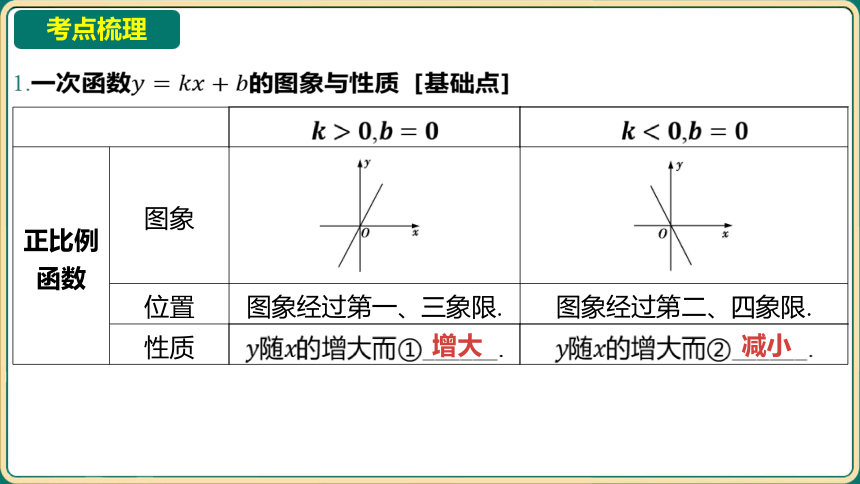
1.一次函数 的图象与性质[基础点]
, ,
正比例 函数 图象 ______________________________ ________________________________
位置 图象经过第一、三象限. 图象经过第二、四象限.
性质 随 的增大而①______. 随 的增大而②______.
增大
减小
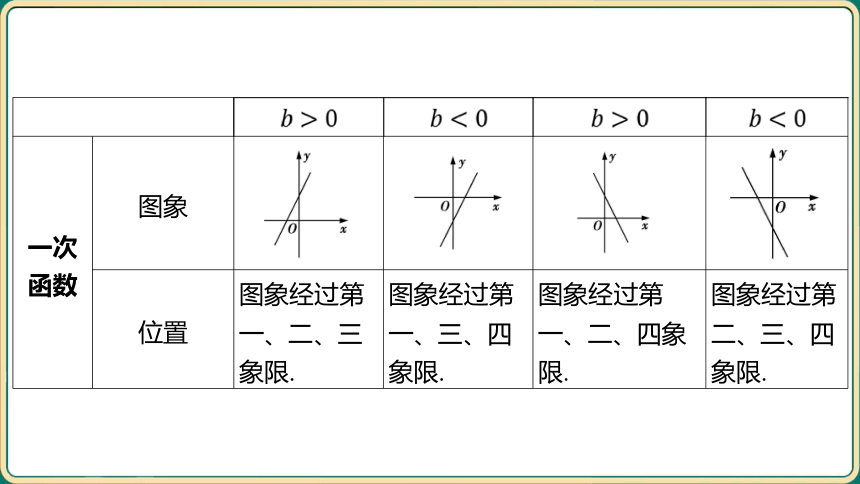
一次 函数 图象 __________________________ ___________________________ ______________________________ ___________________________
位置 图象经过第 一、二、三 象限. 图象经过第 一、三、四 象限. 图象经过第 一、二、四象 限. 图象经过第
二、三、四
象限.
一次 函数 性质 随 的增大而增大. 随 的增大而减小.
图象与坐标 轴的交点 图象与轴的交点坐标为③________,与 轴的交点坐 标为④______.
【提分指南】 ①一次函数图象从左向右看:呈上升趋势 ;呈下降趋势
.
②一次函数的图象与轴的交点:在正半轴;在负半轴 ;恰为原
点 .
回练课本
1.已知一次函数 .
(1)若函数图象经过原点,则 ___;
(2)函数图象与轴的交点坐标为______,与 轴的交点坐标为______;
(用含 的式子表示)
(3)若函数图象经过第二、三、四象限,则 的取值范围为_______;
(4)若点,在该函数的图象上,则, 的大小关系为
________.
0
2.一次函数图象的平移[基础点]
[答案] ; -; ; -
可简记为“左加右减,上加下减”.
【注意】 求直线左右平移后的直线解析式 时,先求出直线
上特殊点平移后的点的坐标,再根据平移后直线的 值不变,代入平移后的
点的坐标求出 的值.
2.直线可以看作是由直线 向下平移___个单位长度得到
的;也可以看作是由直线 向右平移___个单位长度得到的.
4
2
回练课本
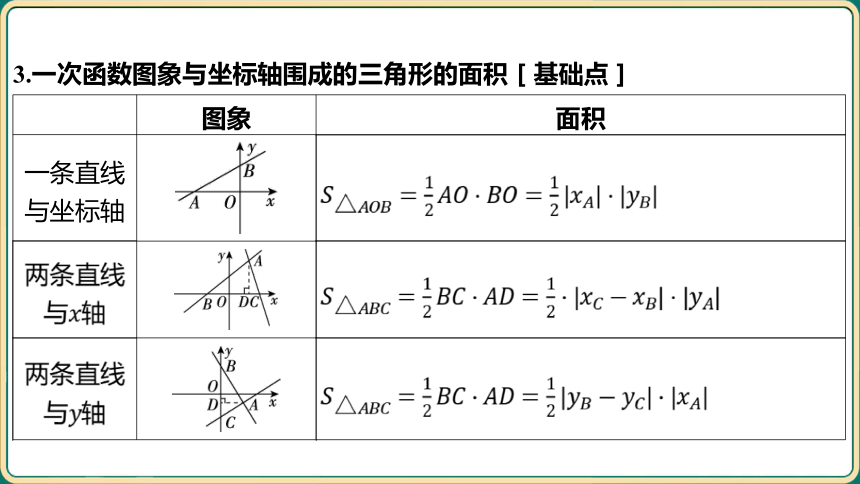
3.一次函数图象与坐标轴围成的三角形的面积[基础点]
图象 面积
一条直线 与坐标轴 ____________________________
两条直线 与 轴 ____________________________
两条直线 与 轴 _____________________________
3.已知直线分别交轴、轴于,两点,为坐标原点,则
的面积为__.
回练课本
4.一次函数解析式的确定[基础点]
一设:设一次函数的解析式为
二列:找出函数图象上的两个点,并将其坐标代人函数解析式中,得到一个方程组.
三解:解方程组,求出待定系数
四还原:将所求待定系数k,的值代人所设的数解析式中.
待定系数法
4.已知一次函数 .
(1)若该函数是正比例函数,则函数的解析式为________.
(2)若该函数的图象经过点 ,则函数的解析式为__________;
(3)若该函数的图象与直线 平行, 则函数的解析式为___________;
(4)不论 为何值, 该函数的图象必经过定点________.
回练课本
5.一次函数与一次方程(组)、一元一次不等式的关系[基础点]
(1)一次函数与一次方程(组)的关系(如图)
.与一元一次方程的关系:方程的解 直线与 轴交
点的横坐标;
.与二元一次方程组的关系:方程组的解 直线
与直线 的交点坐标.
(2)一次函数与一元一次不等式的关系(如图)
.不等式的解集 直线位于 轴⑨_____方的部分对应
的自变量的取值范围;
.不等式的解集 直线位于 轴下方
上
的部分对应的自变量的取值范围;
.不等式的解集 直线位于直线
上方的部分对应的自变量的取值范围.
5.如图,已知直线,直线 ,直线
,分别交轴于,两点,直线, 相交于点
.
(1)关于的方程 的解是______;
(2)关于的不等式的解是________,关于 的不等
式 的解集是______;
(3)关于,的方程组 的解是_ _______;
(4)关于的不等式 的解集是________.
回练课本
考法 一次函数的图象与性质
例 已知一次函数 的图象平行于
直线,且经过点 .
(1)在如图所示的平面直角坐标系中画出函数 的图象与直线
;
[答案] 画图如图所示.
(2)一次函数的图象可以看作是由直线 向___ _平移
_____________个单位长度得到的;
(3)该一次函数的解析式为_____________,函数值随 的增大而______, 若
点,在该函数图象上,则___;(填“ ”“ ”或“ ”)
(4)函数的图象不经过第____象限,与 轴的交点坐标为______,
与 轴的交点坐标为______,与坐标轴围成的三角形的面积为___;
上(右)
2(4)
减小
三
4
(5)不等式的解集为______,当时,自变量 的取值范
围是__________;
(6)若点是一次函数图象上的动点,则 的最小值为
_ ___.
解题通法
根据两函数图象确定不等式解集的方法
1.先确定关键点(两函数图象交点)的坐标.如图,点
2.观察关键点左右两侧图象的位置.
如图,在点左侧,直线在直线下方,则,故 即为不等式
的解集;
在点右侧,直线在直线上方,则,故 即为不等式
的解集.
命题点1 一次函数的图象与性质[8年7考]
(第1题)
1.[2023宁德质检] 如图,已知函数 与
的图象都经过轴上的点,分别与轴交于,
两点,且,两点关于原点对称,则函数 的表达式是
( )
D
A. B. C. D.
(第2题)
2.[2023福州质检] 如图,在平面直角坐标系 中,已知点
,点.若点与点关于直线成轴对称,则直线 的
解析式是( )
C
A. B. C. D.
3.[2024龙岩质检] 平面直角坐标系中,,,则坐标原点
关于直线对称的点 的坐标为( )
B
A. B. C. D.
命题点2 一次函数与一次方程(组)、一元一次
不等式的关系[8年2考]
4.[2021福建中考,8] 如图,一次函数 的图
象过点,则不等式 的解集是( )
C
A. B. C. D.
5.[2023泉州质检] 若不等式的解集是 ,则下列各点可能在一
次函数 的图象上的是( )
A
A. B. C. D.
第三章 函数
第一部分 中考考点梳理
第二节 一次函数的图象与性质
2025年中考数学一轮复习
考点梳理
1.一次函数 的图象与性质[基础点]
, ,
正比例 函数 图象 ______________________________ ________________________________
位置 图象经过第一、三象限. 图象经过第二、四象限.
性质 随 的增大而①______. 随 的增大而②______.
增大
减小
一次 函数 图象 __________________________ ___________________________ ______________________________ ___________________________
位置 图象经过第 一、二、三 象限. 图象经过第 一、三、四 象限. 图象经过第 一、二、四象 限. 图象经过第
二、三、四
象限.
一次 函数 性质 随 的增大而增大. 随 的增大而减小.
图象与坐标 轴的交点 图象与轴的交点坐标为③________,与 轴的交点坐 标为④______.
【提分指南】 ①一次函数图象从左向右看:呈上升趋势 ;呈下降趋势
.
②一次函数的图象与轴的交点:在正半轴;在负半轴 ;恰为原
点 .
回练课本
1.已知一次函数 .
(1)若函数图象经过原点,则 ___;
(2)函数图象与轴的交点坐标为______,与 轴的交点坐标为______;
(用含 的式子表示)
(3)若函数图象经过第二、三、四象限,则 的取值范围为_______;
(4)若点,在该函数的图象上,则, 的大小关系为
________.
0
2.一次函数图象的平移[基础点]
[答案] ; -; ; -
可简记为“左加右减,上加下减”.
【注意】 求直线左右平移后的直线解析式 时,先求出直线
上特殊点平移后的点的坐标,再根据平移后直线的 值不变,代入平移后的
点的坐标求出 的值.
2.直线可以看作是由直线 向下平移___个单位长度得到
的;也可以看作是由直线 向右平移___个单位长度得到的.
4
2
回练课本
3.一次函数图象与坐标轴围成的三角形的面积[基础点]
图象 面积
一条直线 与坐标轴 ____________________________
两条直线 与 轴 ____________________________
两条直线 与 轴 _____________________________
3.已知直线分别交轴、轴于,两点,为坐标原点,则
的面积为__.
回练课本
4.一次函数解析式的确定[基础点]
一设:设一次函数的解析式为
二列:找出函数图象上的两个点,并将其坐标代人函数解析式中,得到一个方程组.
三解:解方程组,求出待定系数
四还原:将所求待定系数k,的值代人所设的数解析式中.
待定系数法
4.已知一次函数 .
(1)若该函数是正比例函数,则函数的解析式为________.
(2)若该函数的图象经过点 ,则函数的解析式为__________;
(3)若该函数的图象与直线 平行, 则函数的解析式为___________;
(4)不论 为何值, 该函数的图象必经过定点________.
回练课本
5.一次函数与一次方程(组)、一元一次不等式的关系[基础点]
(1)一次函数与一次方程(组)的关系(如图)
.与一元一次方程的关系:方程的解 直线与 轴交
点的横坐标;
.与二元一次方程组的关系:方程组的解 直线
与直线 的交点坐标.
(2)一次函数与一元一次不等式的关系(如图)
.不等式的解集 直线位于 轴⑨_____方的部分对应
的自变量的取值范围;
.不等式的解集 直线位于 轴下方
上
的部分对应的自变量的取值范围;
.不等式的解集 直线位于直线
上方的部分对应的自变量的取值范围.
5.如图,已知直线,直线 ,直线
,分别交轴于,两点,直线, 相交于点
.
(1)关于的方程 的解是______;
(2)关于的不等式的解是________,关于 的不等
式 的解集是______;
(3)关于,的方程组 的解是_ _______;
(4)关于的不等式 的解集是________.
回练课本
考法 一次函数的图象与性质
例 已知一次函数 的图象平行于
直线,且经过点 .
(1)在如图所示的平面直角坐标系中画出函数 的图象与直线
;
[答案] 画图如图所示.
(2)一次函数的图象可以看作是由直线 向___ _平移
_____________个单位长度得到的;
(3)该一次函数的解析式为_____________,函数值随 的增大而______, 若
点,在该函数图象上,则___;(填“ ”“ ”或“ ”)
(4)函数的图象不经过第____象限,与 轴的交点坐标为______,
与 轴的交点坐标为______,与坐标轴围成的三角形的面积为___;
上(右)
2(4)
减小
三
4
(5)不等式的解集为______,当时,自变量 的取值范
围是__________;
(6)若点是一次函数图象上的动点,则 的最小值为
_ ___.
解题通法
根据两函数图象确定不等式解集的方法
1.先确定关键点(两函数图象交点)的坐标.如图,点
2.观察关键点左右两侧图象的位置.
如图,在点左侧,直线在直线下方,则,故 即为不等式
的解集;
在点右侧,直线在直线上方,则,故 即为不等式
的解集.
命题点1 一次函数的图象与性质[8年7考]
(第1题)
1.[2023宁德质检] 如图,已知函数 与
的图象都经过轴上的点,分别与轴交于,
两点,且,两点关于原点对称,则函数 的表达式是
( )
D
A. B. C. D.
(第2题)
2.[2023福州质检] 如图,在平面直角坐标系 中,已知点
,点.若点与点关于直线成轴对称,则直线 的
解析式是( )
C
A. B. C. D.
3.[2024龙岩质检] 平面直角坐标系中,,,则坐标原点
关于直线对称的点 的坐标为( )
B
A. B. C. D.
命题点2 一次函数与一次方程(组)、一元一次
不等式的关系[8年2考]
4.[2021福建中考,8] 如图,一次函数 的图
象过点,则不等式 的解集是( )
C
A. B. C. D.
5.[2023泉州质检] 若不等式的解集是 ,则下列各点可能在一
次函数 的图象上的是( )
A
A. B. C. D.
同课章节目录
