2025年中考数学一轮复习 -第三章 函数-第三节 一次函数的实际应用 课件(共29张PPT)
文档属性
| 名称 | 2025年中考数学一轮复习 -第三章 函数-第三节 一次函数的实际应用 课件(共29张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 12:07:15 | ||
图片预览






文档简介
(共29张PPT)
第三章 函数
第一部分 中考考点梳理
第三节 一次函数的实际应用
2025年中考数学一轮复习
考点梳理
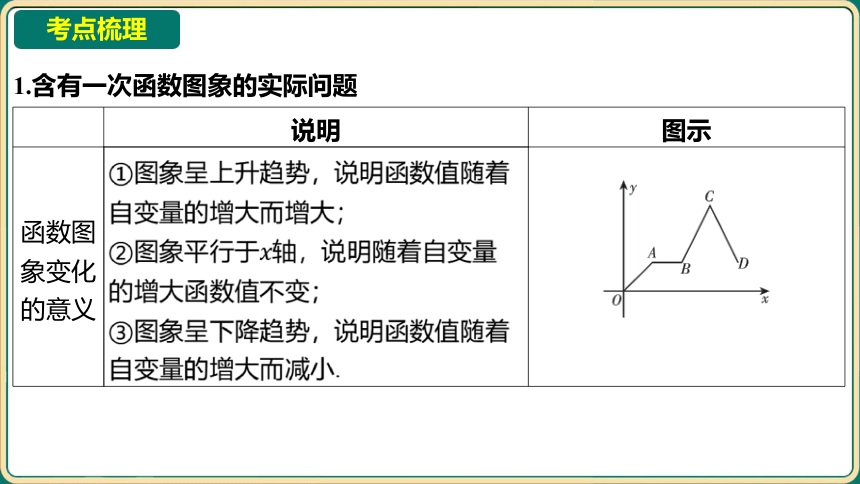
1.含有一次函数图象的实际问题
说明 图示
函数图 象变化 的意义 ①图象呈上升趋势,说明函数值随着 自变量的增大而增大; ②图象平行于 轴,说明随着自变量 的增大函数值不变; ③图象呈下降趋势,说明函数值随着 自变量的增大而减小. _____________________________________________
说明 图示
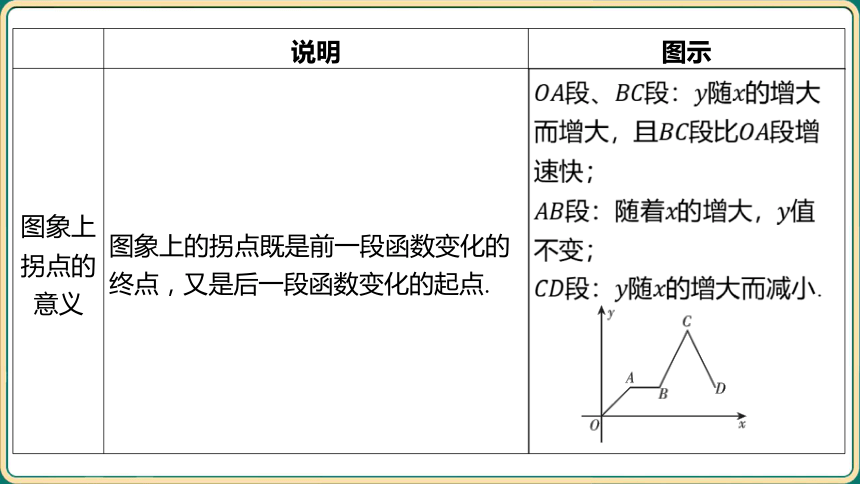
图象上 拐点的 意义 图象上的拐点既是前一段函数变化的 终点,又是后一段函数变化的起点. 段、段:随 的增大
而增大,且段比 段增
速快;
段:随着的增大, 值
不变;
段:随 的增大而减小.
说明 图示
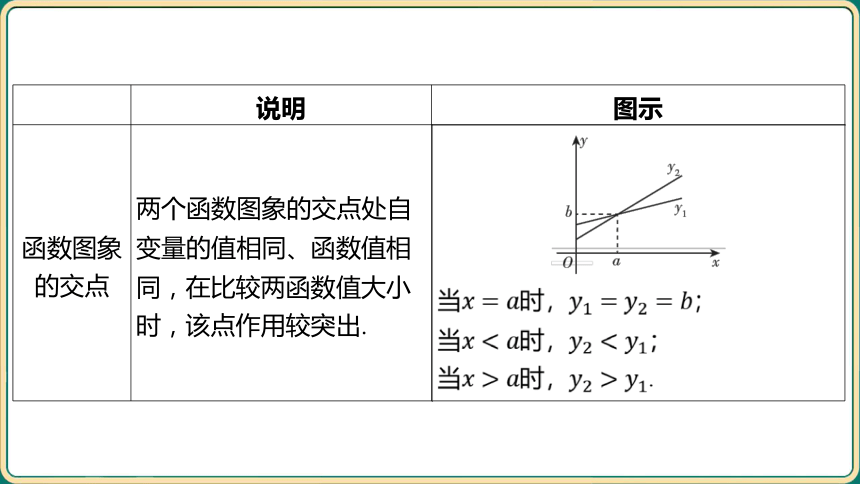
函数图象 的交点 两个函数图象的交点处自 变量的值相同、函数值相 同,在比较两函数值大小 时,该点作用较突出. ____________________________________________
当时, ;
当时, ;
当时, .
回练课本
1.一辆货车先从甲地出发前往乙地,稍后一辆轿车从甲地
驶向乙地.已知甲、乙两地的路程是 ,货车行驶时
的速度是.两车离甲地的路程与时间
的函数关系图象如图.
(1) 的值为____;
(2)轿车离甲地的路程关于时间 的函数解析式为________________;
(3)图象中点 的实际意义是________________________________________
____;
(4)轿车比货车早____ 到达乙地.
1.5
货车出发后,在离甲地处被轿车追上
1.2
2.不含一次函数图象的实际问题
(1)一般解题步骤
①设出问题中的变量,弄清自变量和因变量;
②建立一次函数模型(列一次函数解析式);
③确定自变量的取值范围;
④利用一次函数的性质解决实际问题;
⑤作答.
(2)实际问题中的最大值、最小值
在一次函数的实际应用题中, 根据自变量的取值范围,利用一次函数的增减性
即可求出实际问题中的最值.
2.近年来,中国传统服饰备受大家的青睐,走上国际时装周舞台,大放异
彩.某服装店直接从工厂购进长、短两款传统服饰进行销售,进货价和销售
价如表:
短款 长款
进货价/(元/件) 80 90
销售价/(元/件) 100 120
若该服装店计划购进长、短两款服装共200件(进货价和销售价都不变),
且进货总价不高于16 800元.则服装店应购进短款服装_____件,长款服装
____件,才能获得最大销售利润,最大销售利润是_______元.
120
80
4 800
回练课本
考法 一次函数的实际应用
例1 [2024长春中考] 区间测速是指在某一路段前后设置
两个监控点,根据车辆通过两个监控点的时间来计算车
辆在该路段上的平均行驶速度.小春驾驶一辆小型汽车在
高速公路上行驶,其间经过一段长度为20千米的区间测
速路段,从该路段起点开始,他先匀速行驶 小时,再立即减速以另一速度
匀速行驶(减速时间忽略不计),当他到达该路段终点时,测速装置测得该
辆汽车在整个路段行驶的平均速度为100千米/时.汽车在区间测速路段行驶的
路程(千米)与在此路段行驶的时间 (时)之间的函数图象如图所示.
(1) 的值为__;
[解析] 解法提示:由题意得,, .
(2)当时,求与 之间的函数关系式;
[答案] 设当时,与之间的函数关系式为 ,
则解得
.
(3)通过计算说明在此区间测速路段内,该辆汽车减速前是否超速.
(此路段要求小型汽车行驶速度不得超过120千米/时)
[答案] 当时, ,
先匀速行驶小时的速度为 (千米/时).
, 该辆汽车减速前没有超速.
例2 近年来,市民交通安全意识逐步增强,头盔需求量增大.某商店购进甲、
乙两种头盔,已知购买甲种头盔20只,乙种头盔30只,共花费2 920元,甲
种头盔的单价比乙种头盔的单价高11元.
(1)甲、乙两种头盔的单价分别是多少元?
[答案] 设乙种头盔的单价为元,则甲种头盔的单价为 元.
根据题意,得 ,
解得,则 .
答:甲种头盔的单价是65元,乙种头盔的单价是54元.
(2)商店决定再次购进甲、乙两种头盔共40只,正好赶上厂家进行促销活
动,促销方式如下:甲种头盔按单价的八折出售,乙种头盔每只降价6元出
售.如果此次购买甲种头盔的数量不低于乙种头盔数量的一半,那么购买多
少只甲种头盔,才能使此次购买头盔的总费用最少?最少费用是多少元?
[答案] 设购买只甲种头盔,则购买乙种头盔 只,
根据题意可知,,解得 .
为正整数, 的最小值为14.
设此次购买头盔的总费用为 元,
则 ,
,随 的增大而增大,
当时,的取值最小,此时 .
答:购买14只甲种头盔,能使此次购买头盔的总费用最小,最小费用为1 976
元.
命题点 一次函数的实际应用[8年3考]
1.[2024三明质检] 某学校为开展劳动教育开垦出一块矩形
菜地,菜地的一边靠墙,另外三边用木栏围成,木栏总长为
.如图所示,设矩形菜地一边长为,另一边长为 ,当
B
A.正比例函数关系 B.一次函数关系
C.反比例函数关系 D.二次函数关系
在一定范围内变化时,随的变化而变化,则与 满足的函数关系是( )
2.[2024莆田质检] 花生油的沸点远高于水的沸点,小丽想用刻度不超过
的温度计推算出花生油的沸点.在老师的指导下,她在锅中倒入一些
花生油均匀加热,并每隔 测量一次锅中油温.经老师介绍,在花生油达
到沸点前,锅中油温(单位:)是加热时间(单位: )的一次函数,
得到的数据记录如下:
时间 0 10 20 30 40
油温 10 30 50 70 90
当加热时,油沸腾了,则推算花生油的沸点为_____ .
330
3.[2024南平质检] 北方某市对城市居民冬季的采暖收费标准如下表.
(以户为单位)
阶梯 采暖用气 销售价格
第一阶梯 (含 )的部分 2.67元/
第二阶梯 (含 )的部分 3.15元/
第三阶梯 以上的部分 3.63元/
根据表中所给的数据回答以下问题:
(1)某户用气量为 ,求此户需缴纳的燃气费用;
[答案] (元).
答:此户需缴纳的燃气费用为2 670元.
(2)设某户这个冬季用气量为,缴纳燃气费用为元,求
关于 的函数表达式;
[答案] 当时, .
当 时,
.
关于 的函数表达式为
(3)已知某户这个冬季缴纳燃气费用8 970元,求该户用了多少立方米的燃气.
[答案] 设该户这个冬季用气量为 ,
当用气量为2 500时,
缴纳燃气费用为 (元).
, .
由题意,得 ,
解得 .
答:该户用了 的燃气.
4.[2023龙岩质检] 世界文化遗产——福建土楼(龙岩·永定)是暑期热门的
旅游目的地之一.某土楼纪念品专卖店销售甲、乙两种纪念品,每个甲种纪念
品的进价比每个乙种纪念品的进价多 4元;用400元购进甲种纪念品和用240
元购进乙种纪念品的数量相同.专卖店将每个甲种纪念品售价定为13元,每个
乙种纪念品售价定为8元.
(1)每个甲种纪念品和每个乙种纪念品的进价分别是多少
[答案] 设每个乙种纪念品的进价为元,则每个甲种纪念品的进价为 元,
依题意有 ,
解得 ,
经检验,是原分式方程的解, ,
每个甲种纪念品和每个乙种纪念品的进价分别是10元和6元.
(2)根据市场调查,专卖店计划用不超过3 000元的资金购进甲、乙两种纪念
品共400个,假设这400个纪念品能够全部卖出,求该专卖店获得最大销售利润
的进货方案.
[答案] 设购进甲种纪念品个,那么购进乙种纪念品 个,
进货资金不超过3 000元,
,
解得 ,
该专卖店获得的销售利润 ,
随着 的增大而增大,
当时, 有最大值950,
.
该专卖店获得最大销售利润的进货方案是甲种纪念品进货150个,乙种纪念
品进货250个.
新课标 新考向
【新课标·综合与实践】【问题情境】如何分配工作,使公司支付的总工资
最少?
信息1:某包装公司承接到21 600个旅行包的订单,策划部准备将订单任务
分配给甲、乙两个车间去完成.由于他们的设备与人数不同,甲车间每天生
产的总数是乙车间每天生产总数的2倍,甲车间单独完成这项工作所需的时
间比乙车间单独完成少18天.
信息2:经调查,甲车间每人每天生产60个旅行包,乙车间每人每天生产40
个旅行包.为提高工作效率,人事部到甲、乙两车间抽走相等数量的工
人.策划部为了使抽走后甲、乙两车间每天生产旅行包的总数之和保持不变,
余下的所有工人每天生产旅行包的个数需要提高 .因此,将甲车间每天
的工资提高到3 400元,乙车间每天的工资提高到1 560元.
【问题解决】
任务1:确定工作效率.
(1)求甲、乙车间原来每天分别生产多少个旅行包.
[答案] 设乙车间原来每天生产个旅行包,则甲车间原来每天生产 个旅行
包,
由题意得 ,
解得 ,
经检验, 是原方程的解,且符合题意,
.
答:甲车间原来每天生产1 200个旅行包,乙车间原来每天生产600个旅行包.
任务2:探究抽走人数.
(2)甲、乙车间均被抽走了多少人?
[答案] 由题意知甲车间共有 (人),乙车间共有
(人).
设甲、乙车间均被抽走了 人,
根据题意得 ,
解得 .
答:甲、乙车间均被抽走了3人.
任务3:拟订设计方案.
(3)甲、乙两车间抽走相等数量的工人后,按每人每天生产个数提高
计算,如何安排甲、乙两车间工作的天数,该公司在完成该任务时支付的总
工资最少?最少为多少元?
[答案] 设甲车间工作天,乙车间工作 天,
根据题意得
,
整理得 ,
.
设总工资为 元,则
,
,
随 的增大而减小.
,且, 均为正整数,
为4的倍数,即 的最小值为4,
此时 最大,为29,
当时,最小,最小值为 .
答:安排甲车间工作4天,乙车间工作29天,该公司在完成该任务时支付的
总工资最少,最少为58 840元.
第三章 函数
第一部分 中考考点梳理
第三节 一次函数的实际应用
2025年中考数学一轮复习
考点梳理
1.含有一次函数图象的实际问题
说明 图示
函数图 象变化 的意义 ①图象呈上升趋势,说明函数值随着 自变量的增大而增大; ②图象平行于 轴,说明随着自变量 的增大函数值不变; ③图象呈下降趋势,说明函数值随着 自变量的增大而减小. _____________________________________________
说明 图示
图象上 拐点的 意义 图象上的拐点既是前一段函数变化的 终点,又是后一段函数变化的起点. 段、段:随 的增大
而增大,且段比 段增
速快;
段:随着的增大, 值
不变;
段:随 的增大而减小.
说明 图示
函数图象 的交点 两个函数图象的交点处自 变量的值相同、函数值相 同,在比较两函数值大小 时,该点作用较突出. ____________________________________________
当时, ;
当时, ;
当时, .
回练课本
1.一辆货车先从甲地出发前往乙地,稍后一辆轿车从甲地
驶向乙地.已知甲、乙两地的路程是 ,货车行驶时
的速度是.两车离甲地的路程与时间
的函数关系图象如图.
(1) 的值为____;
(2)轿车离甲地的路程关于时间 的函数解析式为________________;
(3)图象中点 的实际意义是________________________________________
____;
(4)轿车比货车早____ 到达乙地.
1.5
货车出发后,在离甲地处被轿车追上
1.2
2.不含一次函数图象的实际问题
(1)一般解题步骤
①设出问题中的变量,弄清自变量和因变量;
②建立一次函数模型(列一次函数解析式);
③确定自变量的取值范围;
④利用一次函数的性质解决实际问题;
⑤作答.
(2)实际问题中的最大值、最小值
在一次函数的实际应用题中, 根据自变量的取值范围,利用一次函数的增减性
即可求出实际问题中的最值.
2.近年来,中国传统服饰备受大家的青睐,走上国际时装周舞台,大放异
彩.某服装店直接从工厂购进长、短两款传统服饰进行销售,进货价和销售
价如表:
短款 长款
进货价/(元/件) 80 90
销售价/(元/件) 100 120
若该服装店计划购进长、短两款服装共200件(进货价和销售价都不变),
且进货总价不高于16 800元.则服装店应购进短款服装_____件,长款服装
____件,才能获得最大销售利润,最大销售利润是_______元.
120
80
4 800
回练课本
考法 一次函数的实际应用
例1 [2024长春中考] 区间测速是指在某一路段前后设置
两个监控点,根据车辆通过两个监控点的时间来计算车
辆在该路段上的平均行驶速度.小春驾驶一辆小型汽车在
高速公路上行驶,其间经过一段长度为20千米的区间测
速路段,从该路段起点开始,他先匀速行驶 小时,再立即减速以另一速度
匀速行驶(减速时间忽略不计),当他到达该路段终点时,测速装置测得该
辆汽车在整个路段行驶的平均速度为100千米/时.汽车在区间测速路段行驶的
路程(千米)与在此路段行驶的时间 (时)之间的函数图象如图所示.
(1) 的值为__;
[解析] 解法提示:由题意得,, .
(2)当时,求与 之间的函数关系式;
[答案] 设当时,与之间的函数关系式为 ,
则解得
.
(3)通过计算说明在此区间测速路段内,该辆汽车减速前是否超速.
(此路段要求小型汽车行驶速度不得超过120千米/时)
[答案] 当时, ,
先匀速行驶小时的速度为 (千米/时).
, 该辆汽车减速前没有超速.
例2 近年来,市民交通安全意识逐步增强,头盔需求量增大.某商店购进甲、
乙两种头盔,已知购买甲种头盔20只,乙种头盔30只,共花费2 920元,甲
种头盔的单价比乙种头盔的单价高11元.
(1)甲、乙两种头盔的单价分别是多少元?
[答案] 设乙种头盔的单价为元,则甲种头盔的单价为 元.
根据题意,得 ,
解得,则 .
答:甲种头盔的单价是65元,乙种头盔的单价是54元.
(2)商店决定再次购进甲、乙两种头盔共40只,正好赶上厂家进行促销活
动,促销方式如下:甲种头盔按单价的八折出售,乙种头盔每只降价6元出
售.如果此次购买甲种头盔的数量不低于乙种头盔数量的一半,那么购买多
少只甲种头盔,才能使此次购买头盔的总费用最少?最少费用是多少元?
[答案] 设购买只甲种头盔,则购买乙种头盔 只,
根据题意可知,,解得 .
为正整数, 的最小值为14.
设此次购买头盔的总费用为 元,
则 ,
,随 的增大而增大,
当时,的取值最小,此时 .
答:购买14只甲种头盔,能使此次购买头盔的总费用最小,最小费用为1 976
元.
命题点 一次函数的实际应用[8年3考]
1.[2024三明质检] 某学校为开展劳动教育开垦出一块矩形
菜地,菜地的一边靠墙,另外三边用木栏围成,木栏总长为
.如图所示,设矩形菜地一边长为,另一边长为 ,当
B
A.正比例函数关系 B.一次函数关系
C.反比例函数关系 D.二次函数关系
在一定范围内变化时,随的变化而变化,则与 满足的函数关系是( )
2.[2024莆田质检] 花生油的沸点远高于水的沸点,小丽想用刻度不超过
的温度计推算出花生油的沸点.在老师的指导下,她在锅中倒入一些
花生油均匀加热,并每隔 测量一次锅中油温.经老师介绍,在花生油达
到沸点前,锅中油温(单位:)是加热时间(单位: )的一次函数,
得到的数据记录如下:
时间 0 10 20 30 40
油温 10 30 50 70 90
当加热时,油沸腾了,则推算花生油的沸点为_____ .
330
3.[2024南平质检] 北方某市对城市居民冬季的采暖收费标准如下表.
(以户为单位)
阶梯 采暖用气 销售价格
第一阶梯 (含 )的部分 2.67元/
第二阶梯 (含 )的部分 3.15元/
第三阶梯 以上的部分 3.63元/
根据表中所给的数据回答以下问题:
(1)某户用气量为 ,求此户需缴纳的燃气费用;
[答案] (元).
答:此户需缴纳的燃气费用为2 670元.
(2)设某户这个冬季用气量为,缴纳燃气费用为元,求
关于 的函数表达式;
[答案] 当时, .
当 时,
.
关于 的函数表达式为
(3)已知某户这个冬季缴纳燃气费用8 970元,求该户用了多少立方米的燃气.
[答案] 设该户这个冬季用气量为 ,
当用气量为2 500时,
缴纳燃气费用为 (元).
, .
由题意,得 ,
解得 .
答:该户用了 的燃气.
4.[2023龙岩质检] 世界文化遗产——福建土楼(龙岩·永定)是暑期热门的
旅游目的地之一.某土楼纪念品专卖店销售甲、乙两种纪念品,每个甲种纪念
品的进价比每个乙种纪念品的进价多 4元;用400元购进甲种纪念品和用240
元购进乙种纪念品的数量相同.专卖店将每个甲种纪念品售价定为13元,每个
乙种纪念品售价定为8元.
(1)每个甲种纪念品和每个乙种纪念品的进价分别是多少
[答案] 设每个乙种纪念品的进价为元,则每个甲种纪念品的进价为 元,
依题意有 ,
解得 ,
经检验,是原分式方程的解, ,
每个甲种纪念品和每个乙种纪念品的进价分别是10元和6元.
(2)根据市场调查,专卖店计划用不超过3 000元的资金购进甲、乙两种纪念
品共400个,假设这400个纪念品能够全部卖出,求该专卖店获得最大销售利润
的进货方案.
[答案] 设购进甲种纪念品个,那么购进乙种纪念品 个,
进货资金不超过3 000元,
,
解得 ,
该专卖店获得的销售利润 ,
随着 的增大而增大,
当时, 有最大值950,
.
该专卖店获得最大销售利润的进货方案是甲种纪念品进货150个,乙种纪念
品进货250个.
新课标 新考向
【新课标·综合与实践】【问题情境】如何分配工作,使公司支付的总工资
最少?
信息1:某包装公司承接到21 600个旅行包的订单,策划部准备将订单任务
分配给甲、乙两个车间去完成.由于他们的设备与人数不同,甲车间每天生
产的总数是乙车间每天生产总数的2倍,甲车间单独完成这项工作所需的时
间比乙车间单独完成少18天.
信息2:经调查,甲车间每人每天生产60个旅行包,乙车间每人每天生产40
个旅行包.为提高工作效率,人事部到甲、乙两车间抽走相等数量的工
人.策划部为了使抽走后甲、乙两车间每天生产旅行包的总数之和保持不变,
余下的所有工人每天生产旅行包的个数需要提高 .因此,将甲车间每天
的工资提高到3 400元,乙车间每天的工资提高到1 560元.
【问题解决】
任务1:确定工作效率.
(1)求甲、乙车间原来每天分别生产多少个旅行包.
[答案] 设乙车间原来每天生产个旅行包,则甲车间原来每天生产 个旅行
包,
由题意得 ,
解得 ,
经检验, 是原方程的解,且符合题意,
.
答:甲车间原来每天生产1 200个旅行包,乙车间原来每天生产600个旅行包.
任务2:探究抽走人数.
(2)甲、乙车间均被抽走了多少人?
[答案] 由题意知甲车间共有 (人),乙车间共有
(人).
设甲、乙车间均被抽走了 人,
根据题意得 ,
解得 .
答:甲、乙车间均被抽走了3人.
任务3:拟订设计方案.
(3)甲、乙两车间抽走相等数量的工人后,按每人每天生产个数提高
计算,如何安排甲、乙两车间工作的天数,该公司在完成该任务时支付的总
工资最少?最少为多少元?
[答案] 设甲车间工作天,乙车间工作 天,
根据题意得
,
整理得 ,
.
设总工资为 元,则
,
,
随 的增大而减小.
,且, 均为正整数,
为4的倍数,即 的最小值为4,
此时 最大,为29,
当时,最小,最小值为 .
答:安排甲车间工作4天,乙车间工作29天,该公司在完成该任务时支付的
总工资最少,最少为58 840元.
同课章节目录
