2025年中考数学一轮复习 -第三章 函数-第五节 二次函数的图象及其性质（二）课件(共45张PPT)

(共45张PPT)
第三章 函数
第一部分 中考考点梳理
第五节 二次函数的图象及其性质（二）
2025年中考数学一轮复习
考点梳理
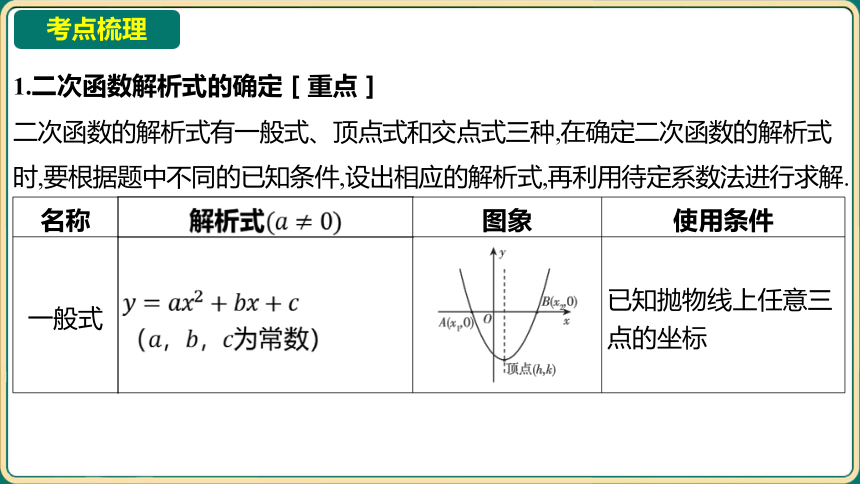
1.二次函数解析式的确定［重点］
二次函数的解析式有一般式、顶点式和交点式三种,在确定二次函数的解析式
时,要根据题中不同的已知条件,设出相应的解析式,再利用待定系数法进行求解.
名称 解析式 图象 使用条件
一般式 （，， 为常数） ______________________________________ 已知抛物线上任意三
点的坐标
名称 解析式 图象 使用条件
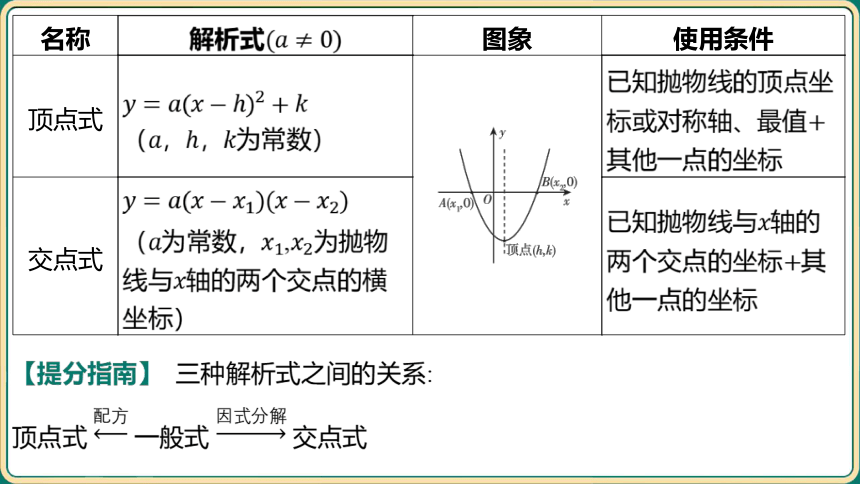
顶点式 （，， 为常数） ______________________________________ 已知抛物线的顶点坐
标或对称轴、最值
其他一点的坐标
交点式 （为常数，, 为抛物 线与 轴的两个交点的横 坐标） 已知抛物线与 轴的
两个交点的坐标 其
他一点的坐标
【提分指南】 三种解析式之间的关系:
顶点式一般式 交点式
回练课本
1.（1）已知二次函数的图象经过与 两点，则这个
二次函数的表达式为_______________；
（2）已知二次函数图象的顶点坐标是，且经过点 ，则这个二
次函数的表达式为__________________；
（3）已知二次函数的图象经过点，和 ，则这个二次函数的表
达式为_____________________.
2.二次函数图象的平移变换［重点］
（1）平移
平移前抛物线的 解析式 平移 个单位 长度 平移后抛物线的解析式 简记
向左 （ ） 左“ ”右“-”
向右 （ ） 向 上“ ”下“-”
向下 1.平移顶点法
（1）将抛物线的解析式化成顶点式，得到顶点 ；
（2）将点平移，得到平移后抛物线的顶点 ；
（3）平移后抛物线的解析式为 .
2.平移任意两点法
先求出原抛物线上任意两点平移后的坐标，再根据二次项系数不变，利用待
定系数法求出平移后抛物线的解析式.
【解题通法】 确定平移后抛物线的解析式的方法
3.直接法
针对一般式,直接进行“上加下减常数项,左加右减自变量”.如将抛物线
向下平移 个单位长度,得到抛物线
;向右平移 个单位长度,得到抛物线
.
2.已知抛物线是由抛物线 向左平移1个单位长度，再向下平移4
个单位长度得到的.
（1）抛物线 的解析式为_________________.
（2）将抛物线 先向上平移3个单位长度,再向右平移2个单位长度,得到的抛
物线的解析式为______________.
（3）将抛物线沿直线向上平移 个单位长度,得到的抛物线的解
析式为_________________.
回练课本
3.二次函数与一元二次方程的关系［重点］
（1）方程的解是二次函数 的图象与
①_____的交点的横坐标.
轴
课标新增：知道二次函数和一元二次方程之间的关系.
（2）判别式决定抛物线与 轴的交点个数.
（ⅰ） ②___0时，抛物线与轴有两个交点，方程 有两个
不相等的实数根；
（ⅱ） ③___0时，抛物线与轴有一个交点，方程 有两个
相等的实数根；
（ⅲ） ④___0时，抛物线与轴没有交点，方程 没有实数根.
3.（1）二次函数的图象与 轴的交点有___个；
（2）二次函数（为常数）的图象与 轴的交点有___个；
（3）抛物线与直线 的交点坐标为_______________.
1
2
,
回练课本
4.二次函数与不等式的关系［重点］
图象 不等式或等式 解集或解
_______________________________________ ⑤_______________
或
⑥____________
____________________________________ ⑦______________
⑧__________
⑨___________
或
或
或
4.如图所示，抛物线的对称轴为直线 ，与直线
交于点和 .
（1）关于的一元二次方程 的解为_________________;
（2）关于的一元二次方程 的解为______________;
（3）关于的不等式 的解集为_____________;
（4）关于的不等式 的解集为__________.
，
,
或
回练课本
考法1 二次函数解析式的确定
例1 已知抛物线 .
（1）若抛物线是由抛物线 向上平移1个单位长度，再向右平移3个单
位长度得到的,则该抛物线的解析式为_________________;
（2）若抛物线过点,， ，则抛物线的解析式为________
___________；
（3）若抛物线的顶点坐标为,且过点 ，则抛物线的解析式为
________________；
（4）若抛物线经过点,,且顶点在 轴上,则抛物线的解析式为
______________;
（5）若抛物线的对称轴为直线,且过点,则与 满足的关系式为
_____________;
（6）若抛物线与轴只有一个交点，且过点,则 的最小值为____；
（7）若抛物线经过点,,且对于抛物线上任意两点 ,
,当时,总有；当 时,
总有 ，则抛物线的解析式为________________；
（8）已知直线交轴于点，交轴于点，抛物线过， 两
点，交轴于另一点，，且对于抛物线上任意两点 ，
，当时，总有 ，则抛物线的解析式为_________
_______________.
解题通法
巧设抛物线解析式的方法
1.若顶点在原点,可设为;
2.若对称轴是轴（或顶点在轴上）,可设为;
3.若顶点在轴上,可设为;
4.若抛物线过原点,可设为;
5.若已知任意三个点的坐标,可设为;
6.若已知顶点,可设为顶点式;
7.若已知抛物线与轴的两交点坐标为,,可设为交点式
.
考法2 二次函数与一元二次方程、不等式的关系
例2 已知抛物线 .
（1）若抛物线经过点,则 _______.
（2）抛物线与 轴的交点坐标为____________.
（3）不等式 的解集是_____________.
3或
,
或
（4）若直线与该抛物线交于,两点,则关于 的方程
的解是______________;关于的不等式 的
解集是__________.
,
（5）将抛物线向上平移 个单位长度.
①若平移后的抛物线与轴没有交点，则 的取值范围为_______.
解法提示：根据题意,得平移后抛物线的解析式为 ，
平移后的抛物线与轴没有交点， 关于的方程 没有实
数根，，解得 .
②若平移后的抛物线与直线只有一个公共点,则 的值为___.
2
解法提示：根据题意,得平移后抛物线的解析式为 ，令
, 平移后的抛物线与直线
只有一个公共点，，解得 .
（6）如图,将抛物线位于轴下方的部分沿轴翻折到 轴上方,得
到一个“”形状的新图象,若直线与新图象有两个公共点,则 的取
值范围为___________________.
或
[解析] 解法提示：抛物线与轴的交点分别为, .当直
线经过点时,；经过点时,.易知抛物线
位于轴下方的部分沿轴翻折到轴上方后对应的解析式为 .令
,整理，得.当直线 与抛物线
没有公共点时,则有,解得, 结合函数
图象可知当直线与新图象有两个公共点时， 的取值范围为
或 .
提分特训
[2024安徽中考节选] 已知抛物线（ 为常数）的顶点横坐标比
抛物线 的顶点横坐标大1.
（1）求 的值.
[答案] 因为抛物线的顶点横坐标为, 的顶点横坐
标为1,
由条件得,解得 .
（2）点在抛物线上,点 在抛物线
上.若,且,,求 的值.
[答案] 因为点在抛物线 上,
所以 .
又点在抛物线 上,
则 .
于是 ,
整理得 .
因为,所以 ,
整理得 .
又,,所以,故,从而 .
命题点 二次函数的综合应用［8年8考］
1.[2024福州质检] 已知抛物线,, .
（1）若抛物线经过点,,与轴的另一个交点是 .
①求抛物线的解析式;
[答案] 将，分别代入 ，得
解得
抛物线的解析式为 .
②过点作轴,垂足为.延长至点,连接,若,求点
的坐标.
[答案] 将代入 ，
得 ，
解得或 ，
，
.
根据题意，得，，， ，
，
.
，
，
.
设，则， .
在中， ，
，
解得 ，
.
（2）当时,已知点,在抛物线上,直线与直线
交于点.若当,时,有
成立,直接写出 的取值范围.
[答案] 或 .
解法提示：设直线的解析式为 ，
将，分别代入，得
解得
直线的解析式为 .
当时， ，
抛物线的对称轴为直线 .
由 可分以下两种情况进行讨论：
①当，，即 时，
， ，
.
又 ，
此时 .
当时，;当 时，
.
若，则
解得 .
②当，，即 时,
， ，
.
又 ，
此时 .
当时，;当时， .
若，则
解得 .
综上所述，或 ．
2.[2024龙岩质检] 抛物线与轴的交点为, ，
顶点为，对称轴与轴的交点为 ．
（1）求抛物线的解析式；
[答案] 方法一：把,分别代入 ，得
解得
抛物线的解析式为 .
方法二：抛物线与轴的交点为, ，
抛物线的解析式为 .
（2）连接，点在线段上，若上存在点，使得 ，且
，求点 的坐标；
[答案] 抛物线的对称轴为直线 ，
顶点为 ，
, .
如图（1），过点作于点，易知 .
由 ，可知 .
又， ，
，
, .
图（1）
方法一：设，则 .
， ，
，即，解得 ，
.
图（1）
方法二：设，则 ，
点的坐标为 .
， ，
用待定系数法求得直线的解析式为 .
将代入，得 ，
解得， .
（3）点是抛物线上的一个动点（不与点,,重合），直线, 分别与
抛物线的对称轴相交于点,，求证：与 的面积相等．
图（2）
证明：如图（2），设点 ，
，且 .
设直线的解析式为 ，
依题意得
解得
直线的解析式为 .
当时， ，
点的坐标为 ，
.
同理可求直线的解析式为 .
当时， ，
点的坐标为 ，
.
图（2）
设点到直线的距离为 ，
则， ，
，
，即与 的面积相等.
图（2）
新课标 新考向
【新考向·新定义】我们定义:若点在一次函数 的图象上,
点在反比例函数的图象上,且满足点与点关于 轴对称,则称
二次函数为一次函数与反比例函数 的“衍生
函数”,点称为“基点”,点 称为“靶点”.
（1）若二次函数是一次函数与反比例函数
的“衍生函数”,则___,___, ___.
1
2
1
（2）若一次函数和反比例函数的“衍生函数”图象的顶点在
轴上,且“基点”的横坐标为1,求“靶点” 的坐标.
[答案] 由题可知“衍生函数”的解析式为,且其图象的顶点在
轴上，
.
“基点” 的横坐标为1，
.
点与点关于 轴对称，
.
反比例函数的解析式为 ，
，
，
“靶点”的坐标为 .
（3）若一次函数和反比例函数 的“衍生函数”
的图象经过点 .
①试说明一次函数 的图象上存在两个不同的“基点”;
[答案] 由题可知“衍生函数”的解析式为 ,且其图象经过点
，
.
，
，
.
设“靶点”,则“基点” ，
，
整理,得 ，
，
方程有两个不相等的实数根，
一次函数 的图象上存在两个不同的“基点”.
②设一次函数图象上两个不同的“基点”的横坐标分别为, ,求
的取值范围.
[答案] 由①可知, ，
, ，
.
，
，
.