2025年中考数学一轮复习 -第三章 函数-第五节 二次函数的图象及其性质(一)课件(共22张PPT)
文档属性
| 名称 | 2025年中考数学一轮复习 -第三章 函数-第五节 二次函数的图象及其性质(一)课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 12:05:45 | ||
图片预览







文档简介
(共22张PPT)
第三章 函数
第一部分 中考考点梳理
第五节 二次函数的图象及其性质(一)
2025年中考数学一轮复习
考点梳理
1. 二次函数的概念[基础点]
形如
次函数,自变量
注:如果明确指出函数是二次函数,那么就隐含了二次项系数不为0这一重
要条件.
回练课本
1.下列函数中,是 的二次函数的是______.(填序号)
;;; ;
; .
①⑤
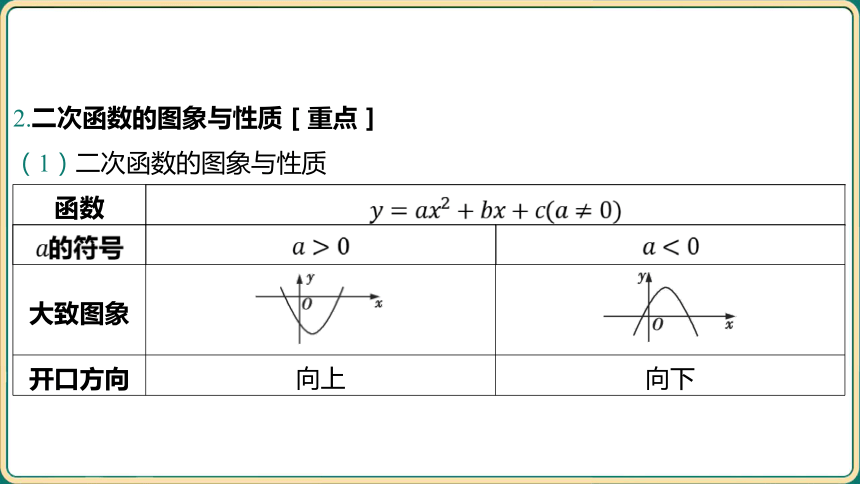
2.二次函数的图象与性质[重点]
(1)二次函数的图象与性质
函数 的符号
大致图象 ____________________________________ ______________________________________
开口方向 向上 向下
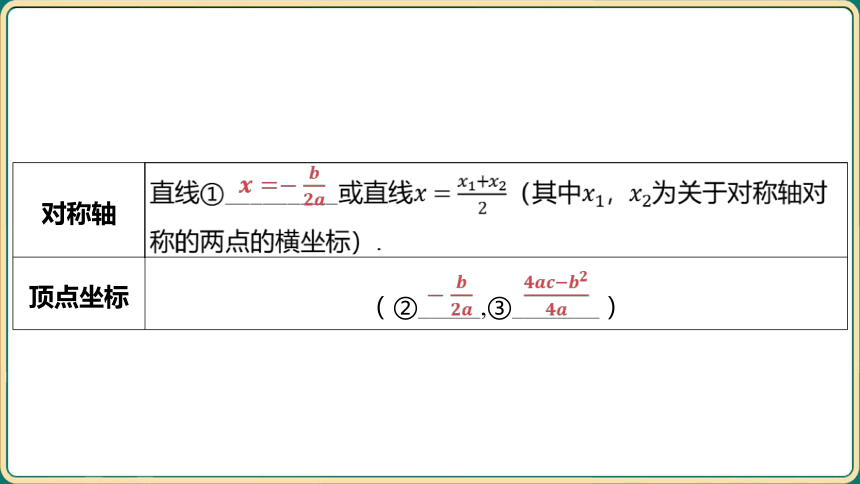
对称轴 直线①_________或直线(其中, 为关于对称轴对
称的两点的横坐标).
顶点坐标 (②_____,③_ ______)
增减性 在对称轴左侧,随 的增大而 ④______. 在对称轴左侧,随 的增大而
⑤______.
在对称轴右侧,随 的增大而 ⑥______. 在对称轴右侧,随 的增大而
⑦______.
最值 当时, 有最⑧____ 值,为 . 当时, 有最⑨____
值,为 .
课标新增:会求二次函数的最大值或最小值,并能确定相应自变量的值.
减小
增大
增大
减小
小
大
(2)抛物线与系数,, 的关系
决定抛物线的开口 方向和大小. ,抛物线开口⑩______; ,抛物线
开口 ______.越大,抛物线开口越小;
越小,抛物线开口越大.
, 决定抛物线的对称 轴的位置. ,同号,对称轴在轴 ______;, 异号,对
称轴在轴 ______;,对称轴为 轴.
决定抛物线与 轴交 点的位置. ,抛物线与轴交于正半轴; ,抛物
线与轴交于负半轴; ,抛物线过原点.
向上
向下
左侧
右侧
特殊 关系 当时, __________.
当时, __________.
若,则当时, ___0.
若,则当时, ___0.
课标新增:知道二次函数系数与图象形状和对称轴的关系.
2.(1)已知二次函数,函数值与自变量 之间的部分对应
数值如下表:
… 0 1 …
… 1 …
①该函数图象的对称轴是直线________,顶点坐标为________;
回练课本
②请在图(1)中画出该函数的图象;
图(1)
[答案] 画出该函数的图象如图所示.
③当时,随 的增大而______;
④当时, 的取值范围是____________.
减小
图(2)
(2)如图(2),二次函数的图象与 轴交
于和两点,对称轴是直线 ,下列结论中:
;②点的坐标为; ;
;
;⑥对于任意实数,都有 .
②③④⑤⑥
其中所有正确的结论是____________. (填序号)
考法1 二次函数的图象与性质
例1 下表中列出的是二次函数的自变量 与函数
的几组对应值:
… 0 1 3 …
… 6 …
根据表格中所提供的数据,完成下列问题:
(1)该抛物线的对称轴为直线______.
(2)该抛物线的解析式为________________,顶点坐标为_________.
(3)该抛物线与轴的交点坐标为________,与 轴的两个交点坐标为
_____________,与 轴的两个交点间的距离为___.
(4)当时,______;当时, 的取值范围为____________
__;当时, 的取值范围为__________.
,
5
0或3
或
(5)若,是该抛物线上两点,且,则实数 的取
值范围是____________.
(6)若点,是该抛物线上不同的两点,且,则 的
值为_______.
(7)该抛物线上的点 关于抛物线的对称轴对称的点的坐标为______.
或5
(8)若点,,在该抛物线上,则,, 的大
小关系是_____________.
(9)若点为该抛物线上一点,且到对称轴的距离为,则点 的坐标为
________________.
(10)若和是抛物线上的两点,则当时,,
的大小关系是________.
或
解题通法
求抛物线的对称轴的方法
1.公式法:抛物线的对称轴为直线 .
2.配方法:将抛物线的解析式配方成顶点式 ,对称轴为直
线 .
3.根据对称性求解:若抛物线上两点的纵坐标相等,则这两点关于抛物线的
对称轴对称,对称轴是这两点连线的垂直平分线,即若抛物线过点 ,
,则对称轴为直线 .
利用二次函数的性质比较函数值大小的方法
1.代入比较法:若已知二次函数的解析式,可将各点的横坐标代入解析式,
求出各点的纵坐标,继而比较大小.
2.增减性比较法:利用二次函数图象的对称性,将已知点转化到对称轴的同
侧,再利用二次函数的增减性比较大小.
3.距离比较法:根据点到对称轴的距离比较大小,具体如下.
对于二次函数
①当 时,抛物线上的点到对称轴的距离越小,对应的函数值越小,如
图(1);
②当 时,抛物线上的点到对称轴的距离越小,对应的函数值越大,如
图(2).
图(1)
图(2)
考法2 二次函数的图象与系数,, 的关系
例2 对称轴为直线 的抛物线
,,为常数,且 如图所示.
(1)与 的数量关系为_________.
(2)___0,___0,___0,___0.(填“ ”“ ”或“ ”)
(3)函数的最小值为__________.
(4)当时,___0;___0;___0; ___0.
(填“ ”“ ”或“ ”)
(5)当时,___0;___0.(填“ ”“ ”或“ ”)
(6)若为任意实数,则___(填“ ”“ ”“ ”或“ ”).
命题点 二次函数的图象与性质[8年8考]
1.[2021福建中考,10] 二次函数 的图象过
,,, 四个点,下列说法一定正确的是( )
C
A.若,则 B.若,则
C.若,则 D.若,则
2.[2024福建中考,10] 已知二次函数 的图象经过
, 两点,则下列判断正确的是( )
C
A.可以找到一个实数,使得 B.无论实数取什么值,都有
C.可以找到一个实数,使得 D.无论实数取什么值,都有
3.[2022福建中考,16] 已知抛物线与轴交于, 两点,抛物线
与轴交于,两点,其中.若,则 的值为___.
8
4.[2023福建中考,16] 已知抛物线 经过
,两点,若, 分别位于抛物线对称轴的两侧,且
,则 的取值范围是____________.
5.[2024龙岩质检] 抛物线经过, ,
,四点,且,若存在正数 ,使得当
时,总有成立,则正数 的取值范围是____________
_______.
或
6.[2024三明质检] 点,在二次函数 的图象
上,若当,时,都有,则 的取值范围
是_______________.
或
7.[2024莆田质检] 已知抛物线过不在 轴上的四个点
,,,.若,,, 四个点中有且只有一
个点在轴上方,则 的取值范围为__________.
第三章 函数
第一部分 中考考点梳理
第五节 二次函数的图象及其性质(一)
2025年中考数学一轮复习
考点梳理
1. 二次函数的概念[基础点]
形如
次函数,自变量
注:如果明确指出函数是二次函数,那么就隐含了二次项系数不为0这一重
要条件.
回练课本
1.下列函数中,是 的二次函数的是______.(填序号)
;;; ;
; .
①⑤
2.二次函数的图象与性质[重点]
(1)二次函数的图象与性质
函数 的符号
大致图象 ____________________________________ ______________________________________
开口方向 向上 向下
对称轴 直线①_________或直线(其中, 为关于对称轴对
称的两点的横坐标).
顶点坐标 (②_____,③_ ______)
增减性 在对称轴左侧,随 的增大而 ④______. 在对称轴左侧,随 的增大而
⑤______.
在对称轴右侧,随 的增大而 ⑥______. 在对称轴右侧,随 的增大而
⑦______.
最值 当时, 有最⑧____ 值,为 . 当时, 有最⑨____
值,为 .
课标新增:会求二次函数的最大值或最小值,并能确定相应自变量的值.
减小
增大
增大
减小
小
大
(2)抛物线与系数,, 的关系
决定抛物线的开口 方向和大小. ,抛物线开口⑩______; ,抛物线
开口 ______.越大,抛物线开口越小;
越小,抛物线开口越大.
, 决定抛物线的对称 轴的位置. ,同号,对称轴在轴 ______;, 异号,对
称轴在轴 ______;,对称轴为 轴.
决定抛物线与 轴交 点的位置. ,抛物线与轴交于正半轴; ,抛物
线与轴交于负半轴; ,抛物线过原点.
向上
向下
左侧
右侧
特殊 关系 当时, __________.
当时, __________.
若,则当时, ___0.
若,则当时, ___0.
课标新增:知道二次函数系数与图象形状和对称轴的关系.
2.(1)已知二次函数,函数值与自变量 之间的部分对应
数值如下表:
… 0 1 …
… 1 …
①该函数图象的对称轴是直线________,顶点坐标为________;
回练课本
②请在图(1)中画出该函数的图象;
图(1)
[答案] 画出该函数的图象如图所示.
③当时,随 的增大而______;
④当时, 的取值范围是____________.
减小
图(2)
(2)如图(2),二次函数的图象与 轴交
于和两点,对称轴是直线 ,下列结论中:
;②点的坐标为; ;
;
;⑥对于任意实数,都有 .
②③④⑤⑥
其中所有正确的结论是____________. (填序号)
考法1 二次函数的图象与性质
例1 下表中列出的是二次函数的自变量 与函数
的几组对应值:
… 0 1 3 …
… 6 …
根据表格中所提供的数据,完成下列问题:
(1)该抛物线的对称轴为直线______.
(2)该抛物线的解析式为________________,顶点坐标为_________.
(3)该抛物线与轴的交点坐标为________,与 轴的两个交点坐标为
_____________,与 轴的两个交点间的距离为___.
(4)当时,______;当时, 的取值范围为____________
__;当时, 的取值范围为__________.
,
5
0或3
或
(5)若,是该抛物线上两点,且,则实数 的取
值范围是____________.
(6)若点,是该抛物线上不同的两点,且,则 的
值为_______.
(7)该抛物线上的点 关于抛物线的对称轴对称的点的坐标为______.
或5
(8)若点,,在该抛物线上,则,, 的大
小关系是_____________.
(9)若点为该抛物线上一点,且到对称轴的距离为,则点 的坐标为
________________.
(10)若和是抛物线上的两点,则当时,,
的大小关系是________.
或
解题通法
求抛物线的对称轴的方法
1.公式法:抛物线的对称轴为直线 .
2.配方法:将抛物线的解析式配方成顶点式 ,对称轴为直
线 .
3.根据对称性求解:若抛物线上两点的纵坐标相等,则这两点关于抛物线的
对称轴对称,对称轴是这两点连线的垂直平分线,即若抛物线过点 ,
,则对称轴为直线 .
利用二次函数的性质比较函数值大小的方法
1.代入比较法:若已知二次函数的解析式,可将各点的横坐标代入解析式,
求出各点的纵坐标,继而比较大小.
2.增减性比较法:利用二次函数图象的对称性,将已知点转化到对称轴的同
侧,再利用二次函数的增减性比较大小.
3.距离比较法:根据点到对称轴的距离比较大小,具体如下.
对于二次函数
①当 时,抛物线上的点到对称轴的距离越小,对应的函数值越小,如
图(1);
②当 时,抛物线上的点到对称轴的距离越小,对应的函数值越大,如
图(2).
图(1)
图(2)
考法2 二次函数的图象与系数,, 的关系
例2 对称轴为直线 的抛物线
,,为常数,且 如图所示.
(1)与 的数量关系为_________.
(2)___0,___0,___0,___0.(填“ ”“ ”或“ ”)
(3)函数的最小值为__________.
(4)当时,___0;___0;___0; ___0.
(填“ ”“ ”或“ ”)
(5)当时,___0;___0.(填“ ”“ ”或“ ”)
(6)若为任意实数,则___(填“ ”“ ”“ ”或“ ”).
命题点 二次函数的图象与性质[8年8考]
1.[2021福建中考,10] 二次函数 的图象过
,,, 四个点,下列说法一定正确的是( )
C
A.若,则 B.若,则
C.若,则 D.若,则
2.[2024福建中考,10] 已知二次函数 的图象经过
, 两点,则下列判断正确的是( )
C
A.可以找到一个实数,使得 B.无论实数取什么值,都有
C.可以找到一个实数,使得 D.无论实数取什么值,都有
3.[2022福建中考,16] 已知抛物线与轴交于, 两点,抛物线
与轴交于,两点,其中.若,则 的值为___.
8
4.[2023福建中考,16] 已知抛物线 经过
,两点,若, 分别位于抛物线对称轴的两侧,且
,则 的取值范围是____________.
5.[2024龙岩质检] 抛物线经过, ,
,四点,且,若存在正数 ,使得当
时,总有成立,则正数 的取值范围是____________
_______.
或
6.[2024三明质检] 点,在二次函数 的图象
上,若当,时,都有,则 的取值范围
是_______________.
或
7.[2024莆田质检] 已知抛物线过不在 轴上的四个点
,,,.若,,, 四个点中有且只有一
个点在轴上方,则 的取值范围为__________.
同课章节目录
