2025年中考数学一轮复习 -第四章 三角形-第一节 线段、角、相交线与平行线 课件（共27张PPT）

(共27张PPT)
第四章 三角形
第一部分 中考考点梳理
第一节 线段、角、相交线与平行线
2025年中考数学一轮复习
考点梳理
1.直线与线段［基础点］
（1）两个基本事实
.直线的基本事实：两点确定一条直线.
.线段的基本事实：两点之间，①______最短.
（2）线段的中点
如图，点把线段分成相等的两条线段与，点叫做线段 的中
点. .
线段
（3）线段的和差运算
如图，点是线段 上一点，则有：
②____ .
③__ .
④___ .
（4）两点之间的距离:连接两点间的线段的长度,叫做这两点的距离.
-
回练课本
1.（1）如图，经过刨平的木板上的， 两个点，可以弹
出一条笔直的墨线，而且只能弹出一条墨线，可以用来解
释这一实际应用的数学知识是( )
B
A.过一点有无数条直线 B.两点确定一条直线
C.两点之间线段最短 D.线动成面
（2）已知线段，在直线上作线段，使得，若 是线段
的中点，则线段 的长为( )
C
A.1 B.3 C.1或3 D.2或3
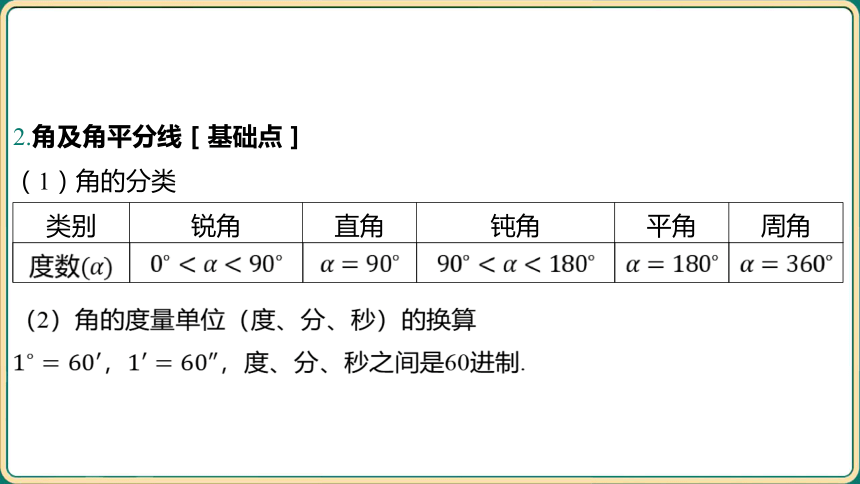
2.角及角平分线［基础点］
（1）角的分类
类别 锐角 直角 钝角 平角 周角
度数
（2）角的度量单位（度、分、秒）的换算
， ，度、分、秒之间是60进制.
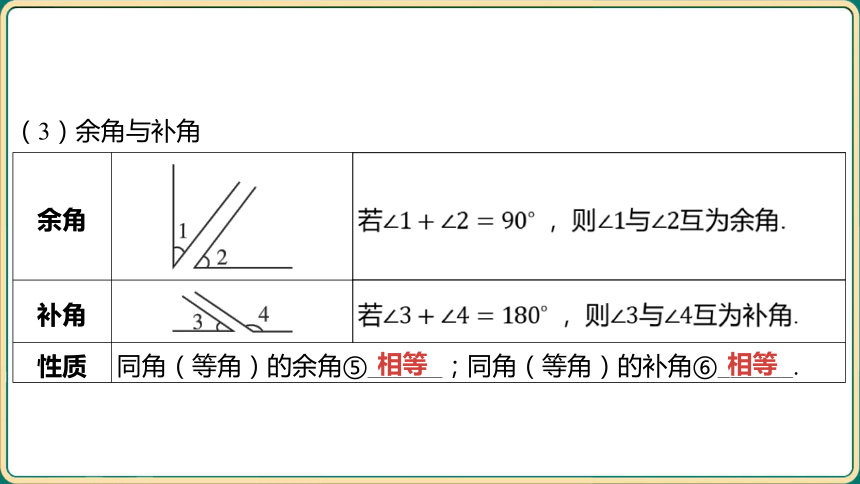
（3）余角与补角
余角 _________________________________ 若 ，则与 互为余角.
补角 __________________________________ 若 ，则与 互为补角.
性质 同角（等角）的余角⑤______；同角（等角）的补角⑥______. 相等
相等
（4）角平分线
文字语言 符号表示 图示
概念 从一个角的顶点引出的一条 射线，把这个角分成两个相 等的角，这条射线叫做这个 角的平分线. 若是 的平分 线，则 ⑦_______ . ___________________________________________
文字语言 符号表示 图示
性质 定理 角平分线上的点到角两边的 距离⑧______. 若平分 ， ， ， 则 . ___________________________________________
性质 定理 的逆 定理 在角的内部，到角两边的距 离⑨______的点在这个角的 平分线上. 若 ， ， ,则点 在 的平分线上. 相等
相等
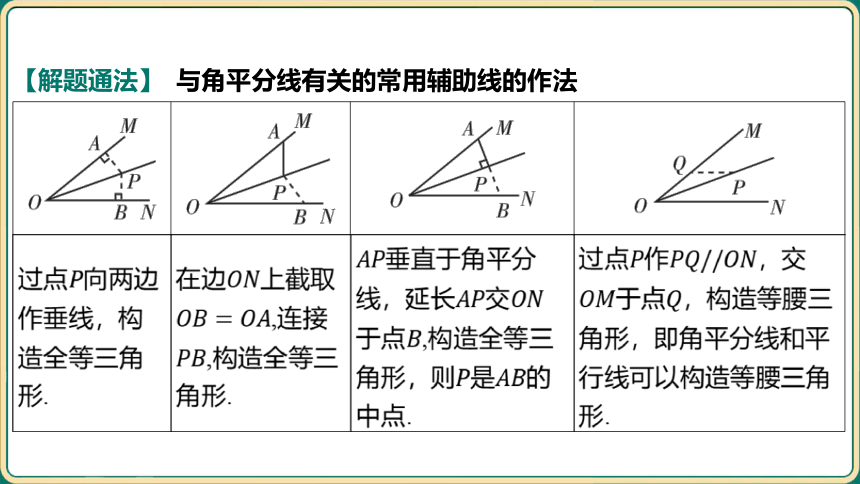
【解题通法】 与角平分线有关的常用辅助线的作法
___________________________________ _________________________________________ ________________________________________ _________________________________________
过点 向两边 作垂线，构 造全等三角 形. 在边 上截取 ,连接 ,构造全等三 角形. 垂直于角平分 线，延长交 于点 ,构造全等三 角形，则是 的 中点. 过点作 ，交
于点 ，构造等腰三
角形，即角平分线和平
行线可以构造等腰三角
形.
2.（1）已知和互为余角，且与互补，，则 的度数
为_________.
图（1）
（2）如图（1）,与是内错角的是____;与 是同位角的是____;
与是同旁内角的是____;与 一定相等的是____.
图（2）
（3）如图（2），，是 的平分线.
若 ，则 的度数是______．
回练课本
图（3）
（4）如图（3），在中， ,以点 为圆心，适
当长为半径作弧，交于点，交于点，分别以点， 为
圆心，大于的长为半径作弧，两弧在的内部交于点 ，
作射线交于点.若，，则 的长为__.
3.垂线及其性质［基础点］
（1）垂线的基本性质
在同一平面内，过一点有且只有⑩____条直线与已知直线垂直；连接直线外
一点与直线上各点的所有线段中， ________最短.
一
垂线段
（2）线段的垂直平分线
文字语言 符号表示 图示
概念 垂直于一条线段，并 且平分这条线段的直 线，叫做这条线段的 垂直平分线. 直线是线段 的垂直平 分线，直线交线段 于 点,则 ， . ______________________________
文字语言 符号表示 图示
性质定理 线段垂直平分线上的 点与这条线段两个端 点的距离相等. 直线是线段 的垂直平 分线，点在直线 上，则 . ______________________________
性质定理 的逆定理 与线段两个端点距离 相等的点在这条线段 的垂直平分线上. 如果，那么点 在 线段 的垂直平分线上. 【易失分点】 判定一条直线是线段的垂直平分线时的误区
判定一条直线是线段的垂直平分线时，需证明直线上有两点到
线段两个端点的距离相等，若直线上只有一个点到线段两个端
点的距离相等，则这条直线不一定是线段的垂直平分线.如
图，，但直线不是线段的垂直平分线.
图（1）
3.（1）如图（1），点，，， 在同一条直线上．在线段
，，， 中，最短的线段是____，理由是_________
___．
垂线段最短
回练课本
图（2）
（2）如图（2），在中， ,,
的垂直平分线交于点，连接.若 ，
则 的长是( )
D
A.10 B.8 C. D.
4.平行线［基础点］
（1）公理及推论
平行公理 经过直线外一点,有且只有一条直线与这条直线平行.
平行公理的推论 如果两条直线都与第三条直线平行，那么这两条直线也
互相平行.
【提分指南】 ①在同一平面内,垂直于同一直线的两条直线平行.
②过平行线上的一点作另一条平行线的垂线,垂线段的长度叫做这两条平行线
间的距离,两条平行线间的距离处处相等.
（2）平行线的判定和性质
同位角 ______ 两直线平行；
内错角相等 两直线 ______；
同旁内角 ______ 两直线平行.
相等
平行
互补
【解题通法】 “折线型”问题中求角度时常作的辅助线类型
“折线型”问题中求角度时，常需要先作辅助线，进而利用平行线的性质求角
度，如,过点作,具体如下表：
图形 ___________________________ __________________________ ________________________________________
结论
4.已知直线 ．
图（1）
（1）如图（1），若 ，可添加一个条件：__________
___________________________________________，判定直线
．
答案不唯一，如 ， ,
图（2）
（2）如图（2），垂直直线于点，交直线于点 ，
若 ，则 的度数为_____．
回练课本
图（3）
（3）如图（3），若平分， ，则 的
度数为_____．
图（4）
（4）如图（4），将一个含 角的三角尺按如图所
示方式放置，直角顶点在直线上，若 ，则
的度数为______.
5.命题［基础点］
（1）命题:判断一件事情的语句,叫做命题.
（2）真命题:如果题设成立,那么结论一定成立,这样的命题叫做真命题.
（3）假命题:如果题设成立时,不能保证结论一定成立,这样的命题叫做假命题.
（4）互逆命题:如果两个命题的题设和结论正好相反,我们把这样的两个命题
叫做互逆命题,如果我们把其中一个叫做原命题,那么另一个叫做它的逆命题.
原命题成立,其逆命题不一定成立.
5.（1）下列命题中，是真命题的是( )
C
A.平行四边形是轴对称图形
B.对角线互相垂直的四边形是菱形
C.到一条线段两个端点距离相等的点，在这条线段的垂直平分线上
D.在中，若，则 是直角三角形
（2）将命题“若，则”的逆命题写成“如果 ，那么……”
的形式：__________________________.
如果，那么
回练课本
命题点1 相交线与平行线［8年1考］
（第1题）
1.[2024福建中考，4] 在同一平面内，将直尺、含 角的三
角尺和木工角尺按如图方式摆放，若 ,则
的大小为( )
A
A. B. C. D.
（第2题）
2.[2024南平质检] 如图,线段和相交于点 ,则下列结论
一定正确的是( )
A
A. B.
C. D.
（第3题）
3.[2023厦门质检] 如图,在四边形中,，点
在边上,平分.下列角中,与 相等的是
( )
C
A. B. C. D.
（第4题）
4.[2024莆田质检] 将一块含 角的直角三角板 按如
图所示的方式放置在纸片上，其中点， 分别落在纸片
边上．若 ，则 的度数为( )
D
A. B. C. D.
（第5题）
5.[2024宁德质检] 如图，直线，交于点 ，
，则____ ．
51
（第6题）
6.[2024三明质检] 如图,,点,分别在直线,
上, , ,则 的度数为_____.
7.[2023厦门质检] 如图,平分,于点,点在射线 上,且
.若,,,则 的长为____.
11
（第7题）