2025年中考数学一轮复习 -第四章 三角形-第二节 一般三角形及其性质 课件(共14张PPT)
文档属性
| 名称 | 2025年中考数学一轮复习 -第四章 三角形-第二节 一般三角形及其性质 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 946.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
第四章 三角形
第一部分 中考考点梳理
第二节 一般三角形及其性质
2025年中考数学一轮复习
考点梳理
1.三角形的分类[基础点]
回练课本
1.如图,在中, , .动点
从点出发,沿边,向点运动.在点 的运动过
程中, 可能成为的特殊三角形依次是______
____________________________________________
__________________.
直角三角形 等边三角形 直角三角形 等腰直角三角形 直角三角形
2.三角形的性质[重点]
(1)三角形具有稳定性.
(2)三边关系:三角形的两边之和①______第三边,两边之差②______第
三边,若一个三角形的三边分别为,,,则 .常用来
判断三条线段能否构成三角形.
大于
小于
(3)边角关系:在同一个三角形中,等边对等角,大边对大角,小边对小角;等角
对等边,大角对大边,小角对小边.
(4)内角和定理:三角形三个内角的和等于③______.
(5)由三角形内角和定理得到的结论:
结论1:直角三角形的两个锐角互余.
结论2:有两个角互余的三角形是直角三角形.
结论3:三角形的外角④______与它不相邻的两个内角的和.
如图, .
等于
结论4:三角形的任意一个外角大于任何一个和它不相邻的
内角.如图,, .
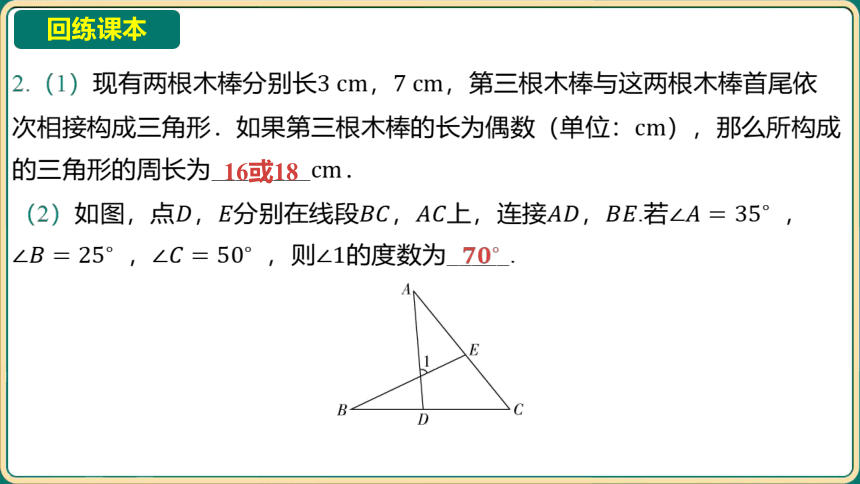
2.(1)现有两根木棒分别长, ,第三根木棒与这两根木棒首尾依
次相接构成三角形.如果第三根木棒的长为偶数(单位: ),那么所构成
的三角形的周长为________ .
16或18
(2)如图,点,分别在线段,上,连接,.若 ,
, ,则 的度数为_____.
回练课本
3.三角形中的重要线段[重点]
中线 高线 角平分线 中位线
图形 ______________________________ 点是 边的中 点,是 的中线. __________________________________ ,垂 足为, 是 的一条 高线. ________________________________ 平分 交于点, 是 的一 条角平分线. _______________________________
点, 分别是边
,的中点,
是 的一条中
位线.
中线 高线 角平分线 中位线
性质 , ,即 且
,
中线 高线 角平分线 中位线
拓展 重心:三角形三条 中线的交点,它到 三角形顶点的距离 等于它到该顶点对 边中点距离的2倍. 垂心:三角形 三条高线的 交点. 内心:三角 形的三条角 平分线的交 点,它到三 角形三边的 距离相等. 当在三角形中遇到
中点时,常构造三角
形中位线,可简单记
为“已知中点找中位
线”.
图(1)
3.(1)如图(1),在中,是边上的高, 平分
.若 , ,则 的度数为_____.
图(2)
(2)如图(2),若和分别是,边上的中线,连接 .
若,,且的周长是16,则的长为___, 的
长为___.
6
3
回练课本
(3)如图(3),在中, ,,分别为 的高
线和中线,,,则 的值为___.
图(3)
命题点11 三角形的边、角关系[8年2考]
1.[2023福建中考,3] 若某三角形的三边长分别为3,4,,则 的值可以
是( )
B
A.1 B.5 C.7 D.9
2.[2024福州质检] 三角形三边的长可以是( )
A
A.,, B.,,
C.,, D.,,
3.[2022漳州质检] 将一副三角尺按如图所示的位置摆放,则 ____度.
45
命题点2 三角形中的重要线段[8年6考]
4.[2022龙岩质检] 如图,中,平分,是 的中点,
,,,则 的长为( )
C
A.1 B. C.2 D.
(第5题)
5.[2022福建中考,12] 如图,在中,,分别是, 的
中点.若,则 的长为___.
6
(第6题)
6.[2021福建中考,14] 如图,是 的角平分线.若
,,则点到 的距离是____.
(第7题)
7.[2022泉州质检] 如图,在中, ,
,,边的垂直平分线分别与, 相
交于点,,则 的周长为___.
7
第四章 三角形
第一部分 中考考点梳理
第二节 一般三角形及其性质
2025年中考数学一轮复习
考点梳理
1.三角形的分类[基础点]
回练课本
1.如图,在中, , .动点
从点出发,沿边,向点运动.在点 的运动过
程中, 可能成为的特殊三角形依次是______
____________________________________________
__________________.
直角三角形 等边三角形 直角三角形 等腰直角三角形 直角三角形
2.三角形的性质[重点]
(1)三角形具有稳定性.
(2)三边关系:三角形的两边之和①______第三边,两边之差②______第
三边,若一个三角形的三边分别为,,,则 .常用来
判断三条线段能否构成三角形.
大于
小于
(3)边角关系:在同一个三角形中,等边对等角,大边对大角,小边对小角;等角
对等边,大角对大边,小角对小边.
(4)内角和定理:三角形三个内角的和等于③______.
(5)由三角形内角和定理得到的结论:
结论1:直角三角形的两个锐角互余.
结论2:有两个角互余的三角形是直角三角形.
结论3:三角形的外角④______与它不相邻的两个内角的和.
如图, .
等于
结论4:三角形的任意一个外角大于任何一个和它不相邻的
内角.如图,, .
2.(1)现有两根木棒分别长, ,第三根木棒与这两根木棒首尾依
次相接构成三角形.如果第三根木棒的长为偶数(单位: ),那么所构成
的三角形的周长为________ .
16或18
(2)如图,点,分别在线段,上,连接,.若 ,
, ,则 的度数为_____.
回练课本
3.三角形中的重要线段[重点]
中线 高线 角平分线 中位线
图形 ______________________________ 点是 边的中 点,是 的中线. __________________________________ ,垂 足为, 是 的一条 高线. ________________________________ 平分 交于点, 是 的一 条角平分线. _______________________________
点, 分别是边
,的中点,
是 的一条中
位线.
中线 高线 角平分线 中位线
性质 , ,即 且
,
中线 高线 角平分线 中位线
拓展 重心:三角形三条 中线的交点,它到 三角形顶点的距离 等于它到该顶点对 边中点距离的2倍. 垂心:三角形 三条高线的 交点. 内心:三角 形的三条角 平分线的交 点,它到三 角形三边的 距离相等. 当在三角形中遇到
中点时,常构造三角
形中位线,可简单记
为“已知中点找中位
线”.
图(1)
3.(1)如图(1),在中,是边上的高, 平分
.若 , ,则 的度数为_____.
图(2)
(2)如图(2),若和分别是,边上的中线,连接 .
若,,且的周长是16,则的长为___, 的
长为___.
6
3
回练课本
(3)如图(3),在中, ,,分别为 的高
线和中线,,,则 的值为___.
图(3)
命题点11 三角形的边、角关系[8年2考]
1.[2023福建中考,3] 若某三角形的三边长分别为3,4,,则 的值可以
是( )
B
A.1 B.5 C.7 D.9
2.[2024福州质检] 三角形三边的长可以是( )
A
A.,, B.,,
C.,, D.,,
3.[2022漳州质检] 将一副三角尺按如图所示的位置摆放,则 ____度.
45
命题点2 三角形中的重要线段[8年6考]
4.[2022龙岩质检] 如图,中,平分,是 的中点,
,,,则 的长为( )
C
A.1 B. C.2 D.
(第5题)
5.[2022福建中考,12] 如图,在中,,分别是, 的
中点.若,则 的长为___.
6
(第6题)
6.[2021福建中考,14] 如图,是 的角平分线.若
,,则点到 的距离是____.
(第7题)
7.[2022泉州质检] 如图,在中, ,
,,边的垂直平分线分别与, 相
交于点,,则 的周长为___.
7
同课章节目录
