2025年中考数学一轮复习 -第四章 三角形-第三节 全等三角形 课件(共30张PPT)
文档属性
| 名称 | 2025年中考数学一轮复习 -第四章 三角形-第三节 全等三角形 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 13:21:17 | ||
图片预览







文档简介
(共30张PPT)
第四章 三角形
第一部分 中考考点梳理
第三节 全等三角形
2025年中考数学一轮复习
考点梳理
1.全等三角形的定义及性质[基础点]
(1)定义:能够完全重合的两个三角形叫做全等三角形.把两个全等三角形重
合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
(2)性质
.全等三角形的对应边①______、对应角②______.
.全等三角形的周长③______、面积④______.
.全等三角形对应的中线、高线、角平分线、中位线都⑤______.
相等
相等
相等
相等
相等
回练课本
1.如图,点,分别在的边,上,连接, 交
于点,连接.若,有如下结论: ;
是等腰三角形;;; 是
的平分线;,是 的两条中线;
①②③⑤⑦⑧
; .则正确的结论为______________.
(填序号)
2.全等三角形的判定[重点]
(1)全等三角形的判定方法
类型 判定方法 图示
一般三角形 三条边分别相等 . _________________________________________________________
两角及它们的夹边分别相等 . __________________________________________________________
类型 判定方法 图示
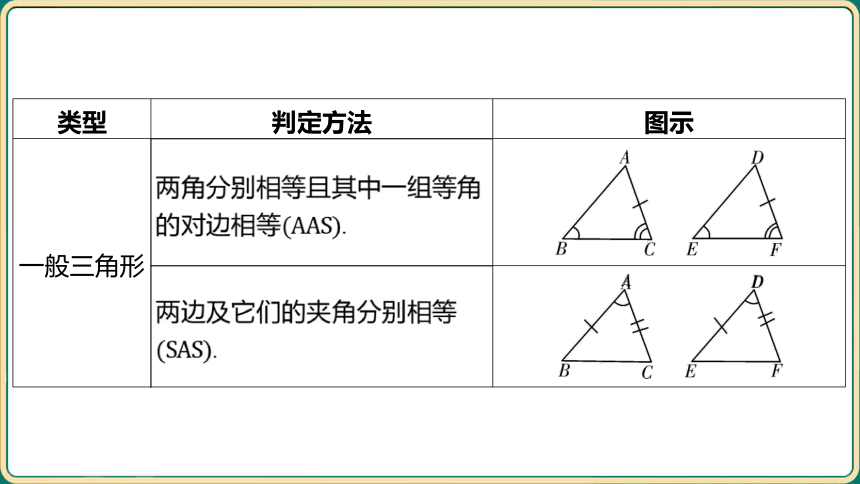
一般三角形 两角分别相等且其中一组等角 的对边相等 . ____________________________________________________________
两边及它们的夹角分别相等 . ___________________________________________________________
类型 判定方法 图示
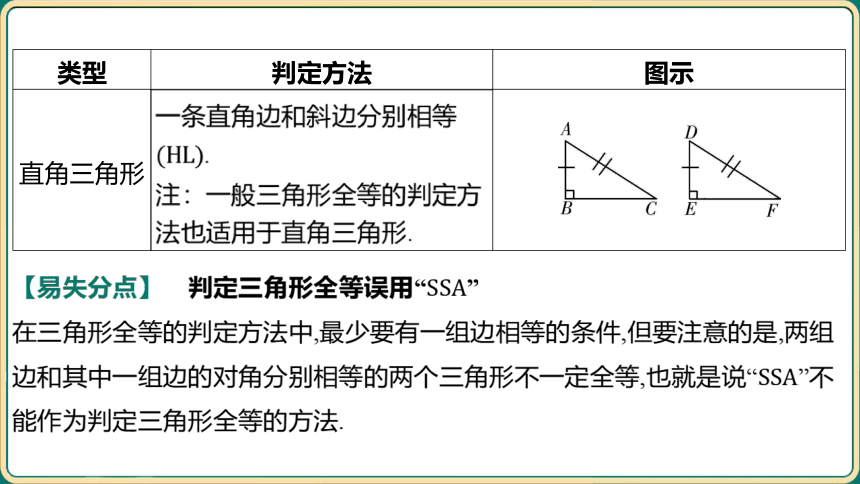
直角三角形 一条直角边和斜边分别相等 . 注:一般三角形全等的判定方 法也适用于直角三角形. _________________________________________________________
【易失分点】 判定三角形全等误用“
在三角形全等的判定方法中,最少要有一组边相等的条件,但要注意的是,两组
边和其中一组边的对角分别相等的两个三角形不一定全等,也就是说“
能作为判定三角形全等的方法.
【提分指南】 “
当两个三角形用符号“
当用“
需要分类讨论,以免漏解.
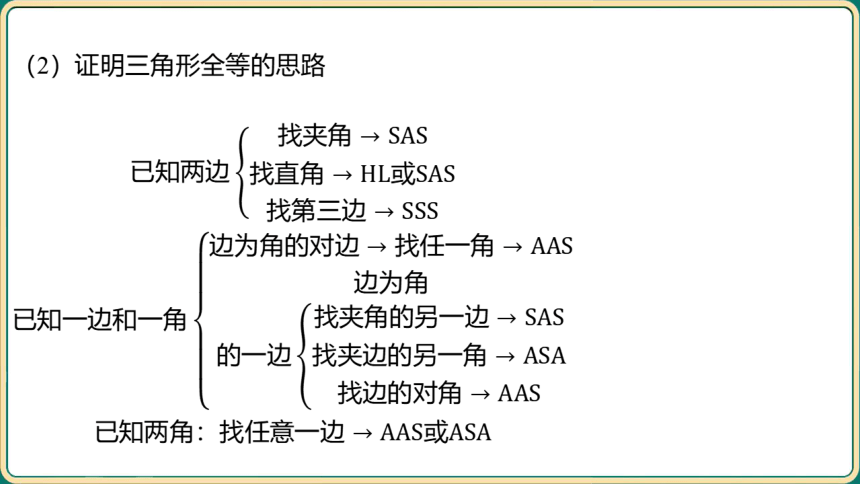
(2)证明三角形全等的思路
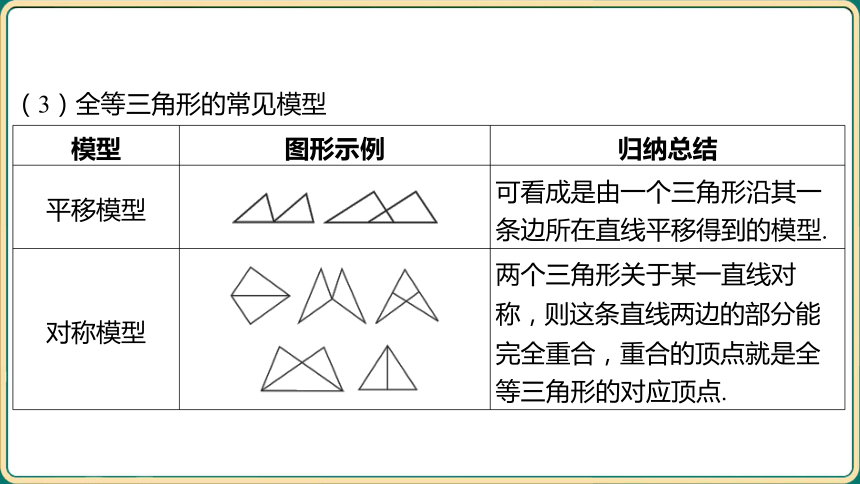
(3)全等三角形的常见模型
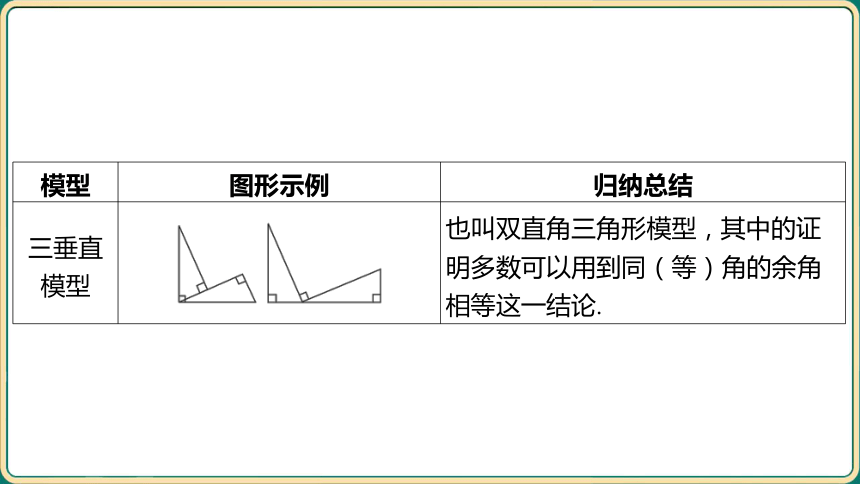
模型 图形示例 归纳总结
平移模型 _______________________________________________________ 可看成是由一个三角形沿其一
条边所在直线平移得到的模型.
对称模型 _______________________________________________________ 两个三角形关于某一直线对
称,则这条直线两边的部分能
完全重合,重合的顶点就是全
等三角形的对应顶点.
模型 图形示例 归纳总结
旋转模型 ________________________________________ _________________________________________________________________________ _________________________________ 可看成是由一个三角形绕某一个点
旋转而成的模型,故一般有一对相
等的角隐含在平行线、对顶角、某
些角的和或者差中.
角平分线 模型 ________________________ 把角平分线看成一条公共边,在角
的两边上截取相等的线段,就可以
构造出全等三角形.
模型 图形示例 归纳总结
三垂直 模型 _____________________________________________________ 也叫双直角三角形模型,其中的证
明多数可以用到同(等)角的余角
相等这一结论.
图(1)
2.(1)如图(1),点,,, 在一条直线上,
, ,请在不添加辅助线的情况下,添
加一个条件,使 ,添加的条件可以是
________________________.
(答案不唯一)
回练课本
(2)如图(2),在中,,点在上(不与点, 重合).
只需添加一个条件即可证明 ,这个条件可以是______________
_______________.(写出一个即可)
为的中点(答案不唯一)
图(2)
(3)如图(3),在中, ,, ,则
的度数为_____.
图(3)
(4)如图(4),,且,作, ,垂足分
别是,.若,,,则线段 的长是___________
(用含,, 的式子表示).
图(4)
(5)如图(5),在中,平分,于点 ,
,若,,则 的值为__.
图(5)
命题点 全等三角形的判定与性质[8年8考]
1.[2024福建中考,18] 如图,在菱形中,点,
分别在边和上,且 .
求证: .
证明: 四边形 是菱形,
, .
在和 中,
,
.
2.[2023福建中考,19] 如图,,, .
求证: .
证明: ,
,
即 .
在和 中,
,
.
3.[2022福建中考,18] 如图,点,,, 在同一条直线上,
,, .
求证: .
证明: ,
,即 .
在和 中,
,
.
4.[2024漳州质检] 如图,在正方形中,为边上一点,为 延长线上
一点,且.求证: .
[答案] 证法一:四边形 是正方形,
, ,
.
在和 中,
,
.
证法二:四边形 是正方形,
, ,
.
在中, ,
在中, ,
, ,
,
.
5.[2024厦门质检] 如图,四边形是矩形,点在边上, ,
垂足为,.求证: .
证明: 四边形 是矩形,
, .
.
,
,
.
,, ,
.
.
6.[2024福州质检] 如图,在中,是 上一点.
(1)在上确定一点,使得 (尺规作图,保留作图痕迹,不写作法).
[答案] 如图(1), 即为所求作的点.
图(1)
(2)在(1)的条件下,当 时,将绕点旋转得到 ,
其中,,分别是点,的对应点.若是的中点,交于点,求证:是
的中点.
证明:是 的中点,
.
图(2)
如图(2),由旋转可知 ,
, ,
,, .
在与 中,
,
,
,即 ,
是 的中点.
图(2)
第四章 三角形
第一部分 中考考点梳理
第三节 全等三角形
2025年中考数学一轮复习
考点梳理
1.全等三角形的定义及性质[基础点]
(1)定义:能够完全重合的两个三角形叫做全等三角形.把两个全等三角形重
合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.
(2)性质
.全等三角形的对应边①______、对应角②______.
.全等三角形的周长③______、面积④______.
.全等三角形对应的中线、高线、角平分线、中位线都⑤______.
相等
相等
相等
相等
相等
回练课本
1.如图,点,分别在的边,上,连接, 交
于点,连接.若,有如下结论: ;
是等腰三角形;;; 是
的平分线;,是 的两条中线;
①②③⑤⑦⑧
; .则正确的结论为______________.
(填序号)
2.全等三角形的判定[重点]
(1)全等三角形的判定方法
类型 判定方法 图示
一般三角形 三条边分别相等 . _________________________________________________________
两角及它们的夹边分别相等 . __________________________________________________________
类型 判定方法 图示
一般三角形 两角分别相等且其中一组等角 的对边相等 . ____________________________________________________________
两边及它们的夹角分别相等 . ___________________________________________________________
类型 判定方法 图示
直角三角形 一条直角边和斜边分别相等 . 注:一般三角形全等的判定方 法也适用于直角三角形. _________________________________________________________
【易失分点】 判定三角形全等误用“
在三角形全等的判定方法中,最少要有一组边相等的条件,但要注意的是,两组
边和其中一组边的对角分别相等的两个三角形不一定全等,也就是说“
能作为判定三角形全等的方法.
【提分指南】 “
当两个三角形用符号“
当用“
需要分类讨论,以免漏解.
(2)证明三角形全等的思路
(3)全等三角形的常见模型
模型 图形示例 归纳总结
平移模型 _______________________________________________________ 可看成是由一个三角形沿其一
条边所在直线平移得到的模型.
对称模型 _______________________________________________________ 两个三角形关于某一直线对
称,则这条直线两边的部分能
完全重合,重合的顶点就是全
等三角形的对应顶点.
模型 图形示例 归纳总结
旋转模型 ________________________________________ _________________________________________________________________________ _________________________________ 可看成是由一个三角形绕某一个点
旋转而成的模型,故一般有一对相
等的角隐含在平行线、对顶角、某
些角的和或者差中.
角平分线 模型 ________________________ 把角平分线看成一条公共边,在角
的两边上截取相等的线段,就可以
构造出全等三角形.
模型 图形示例 归纳总结
三垂直 模型 _____________________________________________________ 也叫双直角三角形模型,其中的证
明多数可以用到同(等)角的余角
相等这一结论.
图(1)
2.(1)如图(1),点,,, 在一条直线上,
, ,请在不添加辅助线的情况下,添
加一个条件,使 ,添加的条件可以是
________________________.
(答案不唯一)
回练课本
(2)如图(2),在中,,点在上(不与点, 重合).
只需添加一个条件即可证明 ,这个条件可以是______________
_______________.(写出一个即可)
为的中点(答案不唯一)
图(2)
(3)如图(3),在中, ,, ,则
的度数为_____.
图(3)
(4)如图(4),,且,作, ,垂足分
别是,.若,,,则线段 的长是___________
(用含,, 的式子表示).
图(4)
(5)如图(5),在中,平分,于点 ,
,若,,则 的值为__.
图(5)
命题点 全等三角形的判定与性质[8年8考]
1.[2024福建中考,18] 如图,在菱形中,点,
分别在边和上,且 .
求证: .
证明: 四边形 是菱形,
, .
在和 中,
,
.
2.[2023福建中考,19] 如图,,, .
求证: .
证明: ,
,
即 .
在和 中,
,
.
3.[2022福建中考,18] 如图,点,,, 在同一条直线上,
,, .
求证: .
证明: ,
,即 .
在和 中,
,
.
4.[2024漳州质检] 如图,在正方形中,为边上一点,为 延长线上
一点,且.求证: .
[答案] 证法一:四边形 是正方形,
, ,
.
在和 中,
,
.
证法二:四边形 是正方形,
, ,
.
在中, ,
在中, ,
, ,
,
.
5.[2024厦门质检] 如图,四边形是矩形,点在边上, ,
垂足为,.求证: .
证明: 四边形 是矩形,
, .
.
,
,
.
,, ,
.
.
6.[2024福州质检] 如图,在中,是 上一点.
(1)在上确定一点,使得 (尺规作图,保留作图痕迹,不写作法).
[答案] 如图(1), 即为所求作的点.
图(1)
(2)在(1)的条件下,当 时,将绕点旋转得到 ,
其中,,分别是点,的对应点.若是的中点,交于点,求证:是
的中点.
证明:是 的中点,
.
图(2)
如图(2),由旋转可知 ,
, ,
,, .
在与 中,
,
,
,即 ,
是 的中点.
图(2)
同课章节目录
