2025年中考数学一轮复习 -第四章 三角形-第五节 相似三角形及其应用 课件(共42张PPT)

(共42张PPT)
第四章 三角形
第一部分 中考考点梳理
第五节 相似三角形及其应用
2025年中考数学一轮复习
考点梳理
1.比例线段［基础点］
比例的性质 （1）基本性质：①____ .
（2）合比性质：如果，那么 .
（3）等比性质：如果 ，那么
.
黄金分割 如图，在线段上，点把线段分成两条线段 和
，如果，那么称线段被点 黄金分
割，点叫做线段的②____________，与 的比叫做黄
金比，即 .一条线段有两个黄金分割点.
____________________________________
黄金分割点
回练课本
1.（1）已知,则 的值为__.
（2）如图，点把线段分成两条线段和，如果 ，则称
线段被点黄金分割，点叫做线段 的黄金“右割”点，根据图形不难发
现，线段上另有一点把线段分成两条线段和，若 ，
则称点是线段的黄金“左割”点.若，则 _________.
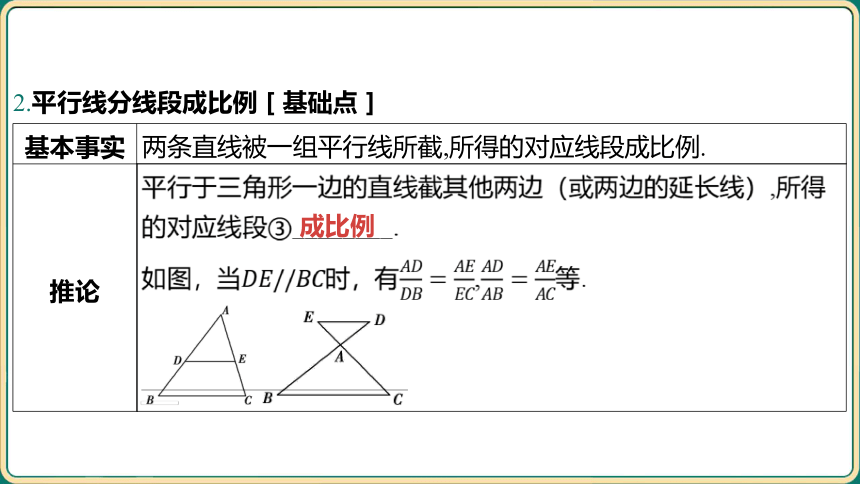
2.平行线分线段成比例［基础点］
基本事实 两条直线被一组平行线所截,所得的对应线段成比例.
推论 平行于三角形一边的直线截其他两边（或两边的延长线）,所得
的对应线段③________.
如图，当时，有, 等.
___________________________________________________________________
成比例
2.（1）如图（1），直线，，被直线，所截，交点分别为点，，
和点，，.已知，且，,则 的长是____.
14
图（1）
图（2）
（2）如图（2）,在中,,且,则 的值为__.
回练课本
3.相似三角形的判定与性质［重点］
（1）性质
.相似三角形的对应角相等，对应边成比例；
.相似三角形对应高的比、对应中线的比和对应角平分线的比都④______相
似比；
.相似三角形的周长比等于⑤________，面积比等于⑥______________.
等于
相似比
相似比的平方
【注意】 勿因混淆平行线分线段成比例与相似三角形对应边成比例而致错.
（2）判定
语言叙述 图示
两角分别相等的两个三角形相似. ____________________________________________
两边成比例且夹角相等的两个三角形相似. ______________________________________________
三边成比例的两个三角形相似. ________________________________________________
【解题通法】 判定两个三角形相似的思路
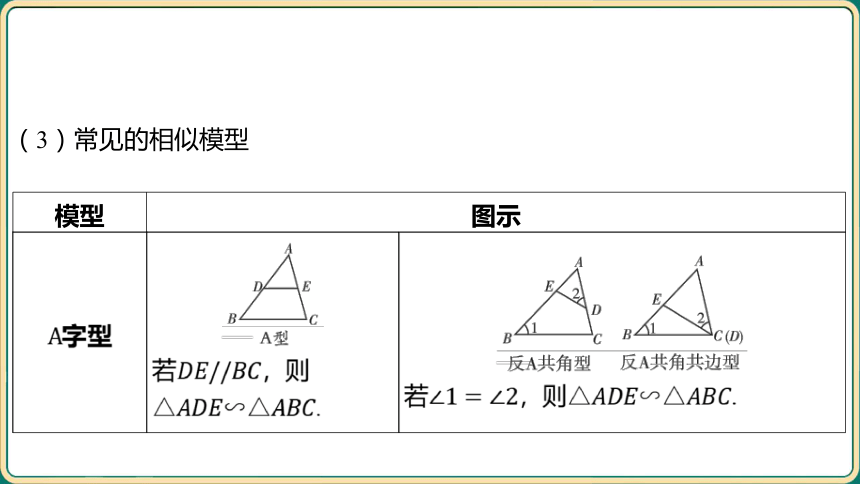
（3）常见的相似模型
模型 图示 字型 __________________________ 若 ，则 . _______________________________________________________________
若，则 .
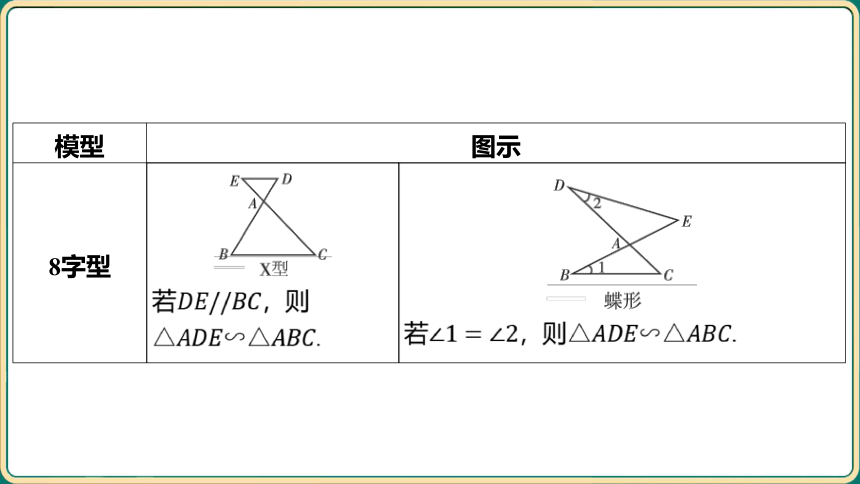
模型 图示 8字型 ______________________________ 若 ，则 . ______________________________________
若，则 .
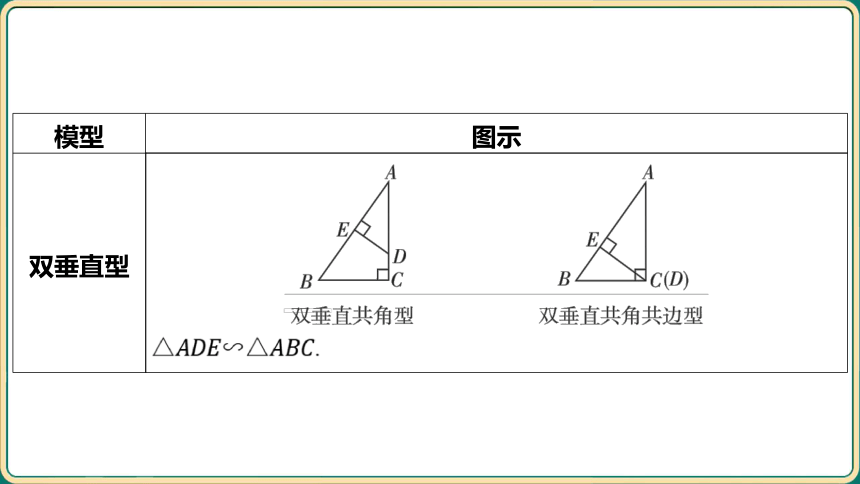
模型 图示
双垂直型 __________________________________________________________________________________________________________
.
模型 图示
一线三等 角型 _______________________________________________________________________________________________
若,则 .
【易失分点】 “两个三角形相似”与“ ”的区别
利用相似三角形解决问题时,要注意相似三角形中的对应关系,弄清两个三角
形的对应边、对应角,从而得到正确的比例关系.如果题中只给出两个三角形
相似,而不是“”,那么需要分情况讨论.
图（1）
3.（1）如图（1），在中，， ，则下列结
论中正确的是( )
C
A. B.
C. D.
图（2）
（2）如图（2），平行四边形中，是边上一点，
交于点，如果，那么 的值为__．
回练课本
（3）如图（3），等边三角形中，为边上的一点，为 边上的一
点，且 ,,,则 的边长为____.
16
图（3）
（4）在中,,,点是的中点,点在上,连接 ,若
和相似,则 的长为_____.
或
4.相似三角形的实际应用［难点］
（1）常见的两种实际应用类型
.测量高度:测量不能达到顶端的物体的高度,通常利用“在同一时刻物高与影
长成比例”构造相似三角形求解.
.测量距离:测量不能直接到达的两点间的距离,常通过构造相似三角形求解.
（2）运用相似三角形的判定条件和性质解决实际问题的一般步骤
.将实际问题转化为相似三角形问题.
.找出一对相似三角形.
.根据相似三角形的性质,表示出相应的量,列比例式求解.
4.如图,数学活动课上,为测量学校旗杆高度,小菲同学在脚
下水平放置一平面镜,然后向后退（保持脚、镜和旗杆底
端在同一直线上）,直到她刚好在镜子中看到旗杆的顶端.
8
已知小菲的眼睛离地面高度为,同时量得小菲与镜子的水平距离为 ,
镜子与旗杆的水平距离为,则旗杆高度为___ .
回练课本
5.相似多边形［基础点］
（1）定义:两个边数相同的多边形,如果它们的角分别相等,边对应成比例,那
么这两个多边形叫做相似多边形.
（2）性质: .相似多边形的对应角⑦______，对应边成比例；
.相似多边形的周长比等于⑧________，面积比等于⑨______________.
相等
相似比
相似比的平方
5.如图，矩形的对称轴交于点,交于点 .若矩形
与矩形相似，则 的值为____.
回练课本
考法 相似三角形的性质与判定
例1 【基础巩固】
（1）如图（1），在中，为上一点，连接，为 上一点，
连接，若，，求证： ．
证明： ，
，
，
.
,
.
图（1）
【尝试应用】
（2）如图（2），在平行四边形中，对角线,交于点,为 上一
点，连接，，，若,，求 的长．
图（2）
[答案] 四边形 是平行四边形，
， ，
，
，
，
.
又 ，
，
图（2）
.
设，则 ，
，
解得, （舍去），
，
.
图（2）
例2 在平行四边形中,,分别为边, 上的点,且
,连接 .
（1）如图（1）,若,在上截取,连接,求证: ；
证明： 四边形是平行四边形， ，
， ， ，
.
，
， 为等边三角形，
图（1）
， ，
.
， ，
，
，
，
，
.
图（1）
（2）如图（2）,若,,求 的值.
图（2）
[答案] 如图，在上截取，连接 .
同（1）易得 .
又 ，
．
又 ，
，
.
设，则， .
易知 是等边三角形，
， ，
，
.
设，则， ，
.
，
.
，
，
， ，
．
提分特训
1.如图,,于点,点在上,点在上, .作
于点,点在上,且，连接.求证: .
[答案] 证法一：， ，
.
又 ，
，
， ，
， ，
，
，
.
又 ，
.
证法二：， ，
，
，，， 四点共圆，
，
.
又 ，
.
2.[2024广西中考改编] 如图（1），中， ， 的垂
直平分线分别交，于点，，平分 .
图（1）
图（2）
（1）求证： .
证明：为 的垂直平分线，
， .
平分 ，
，
.
又 ，
.
（2）如图（2），将绕点逆时针旋转得到 ，旋转角为
.连接，.当是直角三角形时，求旋转角
的度数.
[答案] 如图（1），易知点，均在以点为圆心， 长为半径的圆上，
图（1）
若或为 ，则线段或为 的直径，很显然，这
是不可能的，
当是直角三角形时， .
当点与点重合时， ，且经过点 ，如图（2），
此时 .
当点与点重合时， ，且经过点 ，如图（3），
此时 .
图（2）
图（3）
综上可知，旋转角
的度数为 或 .
命题点 相似三角形的判定与性质［8年8考］
（第1题）
1.[2024南平质检] 如图,在中,,分别是边, 的中点,
则与四边形 的面积之比为( )
C
A. B.
C. D.
（第2题）
2.[2020福建中考，3] 如图,面积为1的等边三角形中,,,
分别是,,的中点,则 的面积是( )
D
A.1 B. C. D.
（第3题）
3.[2023宁德质检] 如图,,,相交于点 ,若
,,则 的长是___.
6
（第4题）
4.[2021龙岩质检] 将含 角且大小不等的两个直角三角板
按如图所示方式摆放，使直角顶点重合，连接， ，则
____.
5.[2023泉州质检] 如图，在中，点是 的内心.
（1）求作过点且平行于的直线，与,分别相交于点, （要求：尺
规作图，不写作法，保留作图痕迹）;
[答案] 如图（1）、图（2）、图（3）、图（4）所示， 即是所求作的直
线.（作法不唯一，正确作出一种即可）
图（1）
图（2）
图（3）
图（4）
（2）若,,,求 的长.
图（5）
[答案] 如图（5），连接, .
点是的内心，平分 ,
.
,
,
,
,同理可证 .
, ,
的周长 ,
,
,
,
,解得 .