2025年中考数学一轮复习 -第四章 三角形-第四节 等腰三角形与直角三角形 课件(共43张PPT)
文档属性
| 名称 | 2025年中考数学一轮复习 -第四章 三角形-第四节 等腰三角形与直角三角形 课件(共43张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 00:00:00 | ||
图片预览









文档简介
(共43张PPT)
第四章 三角形
第一部分 中考考点梳理
第四节 等腰三角形与直角三角形
2025年中考数学一轮复习
考点梳理
1.等腰三角形和等边三角形[重点]
等腰三角形 等边三角形
性质 (1)两腰相等,两底角 ①______; (2)顶角平分线、底边上的中 线、底边上的高互相重合 (简写成“三线合一”); (3)是轴对称图形,有②____ 条对称轴. (1)三边都相等,三个内角都相
等,且都等于③_____;
(2)每条边上的中线、该边上的
高和该边所对角的平分线互相重
合;
(3)是轴对称图形,有④____条对
称轴.
相等
一
三
等腰三角形 等边三角形
判定 (1)有两条边相等的三角形是 等腰三角形. (2)有两个角相等的三角形是 等腰三角形. (1)三边都相等的三角形是等边
三角形.
(2)三个内角都相等的三角形是
等边三角形.
(3)有一个内角等于 的等腰
三角形是等边三角形.
面积 (为底边 上的高). (为任意边 上
的高).
【易失分点】 解决与等腰三角形有关的问题时的易错点
①已知等腰三角形的一个角,求其他角的度数时,要对该角是顶角还是底角
进行分类讨论.
②求等腰三角形的一条边:当已知等腰三角形的两边时,除了要确定哪条边
作为腰或底边外,还要判断是否满足三角形的三边关系.
回练课本
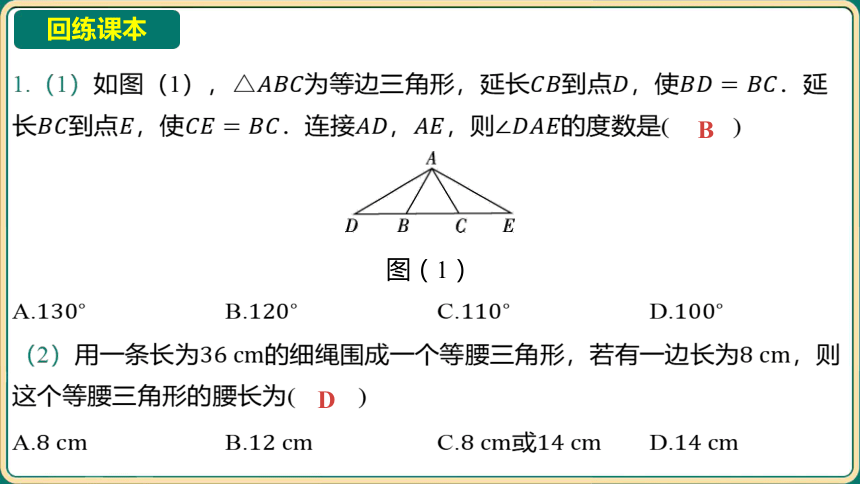
1.(1)如图(1),为等边三角形,延长到点,使 .延
长到点,使.连接,,则 的度数是( )
图(1)
B
A. B. C. D.
(2)用一条长为的细绳围成一个等腰三角形,若有一边长为 ,则
这个等腰三角形的腰长为( )
D
A. B. C.或 D.
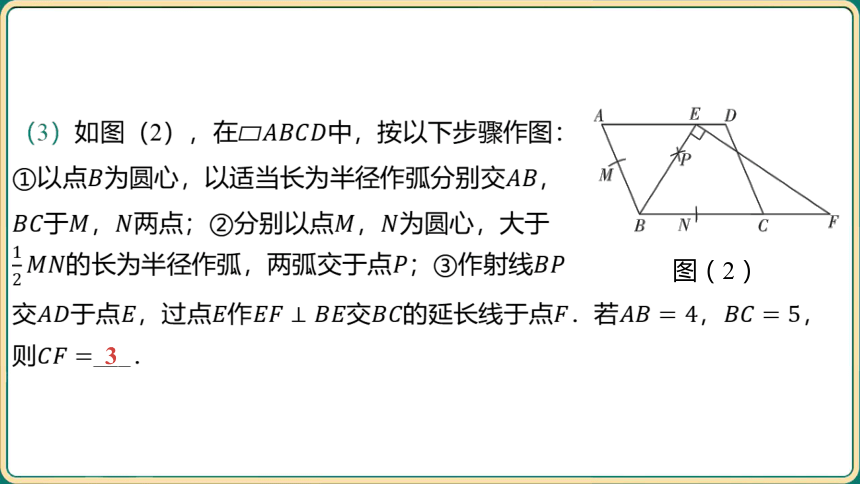
图(2)
(3)如图(2),在 中,按以下步骤作图:
①以点为圆心,以适当长为半径作弧分别交 ,
于,两点;②分别以点, 为圆心,大于
的长为半径作弧,两弧交于点;③作射线
3
交于点,过点作交的延长线于点.若, ,
则 ___.
2.直角三角形[重点]
直角三角形 等腰直角三角形
性质 (1)两锐角互余; (2)斜边上的中线等于斜边的一半; 角所对的直角边等于斜边的一 半; (4)勾股定理:直角三角形中两直角边 的平方和等于斜边的平方,即 (,为直角边, 为斜 边). (1)两直角边相等;
(2)两锐角相等且都等
于 ;
(3)是轴对称图形,有
一条对称轴.
直角三角形 等腰直角三角形
判定 (1)有一个角为 的三角形是 直角三角形; (2)勾股定理的逆定理:若三角 形的三边长,, 满足 ,则该三角形是直角 三角形. 【拓展】 如果三角形的一边上的 中线等于这条边的一半,那么这 个三角形是直角三角形. (1)顶角为 的等腰三角
形是等腰直角三角形;
(2)有两个角是 的三角
形是等腰直角三角形;
(3)有一个角是 的直角
三角形是等腰直角三角形;
(4)两直角边相等的直角三
角形是等腰直角三角形.
直角三角形 等腰直角三角形
面积 (, 为直角边, 为斜边, 为斜边上的高). ( 为直角边,
为斜边, 为斜边上的高).
【解题通法】 解与直角三角形有关的计算题的常用思路
①当出现
②当出现斜边上的中线时,要想到直角三角形中斜边上的中线等于斜边的一半.
③作辅助线构造直角三角形,利用勾股定理或三角函数求线段长或角度.
④已知直角三角形的三边求斜边上的高时,用面积法求解.
⑤已知三角形为直角三角形,但没有明确直角顶点,则需要分类讨论.
图(1)
2.(1)如图(1),已知,边的长为4,以 为
边作正方形,设面积为.以为边作正方形 ,
设面积为.则 的值为____.
16
图(2)
(2)如图(2),点在的边上,点是 的
中点,连接,,若,, ,
,则 的长为____.
回练课本
图(3)
(3)如图(3),在中,是 边上的点,
,,分别是,边的中点,若,则
的长为___.
3
图(4)
(4)如图(4),已知 ,点在边 上,
,点,在边上,.若 ,则
的周长是____.
16
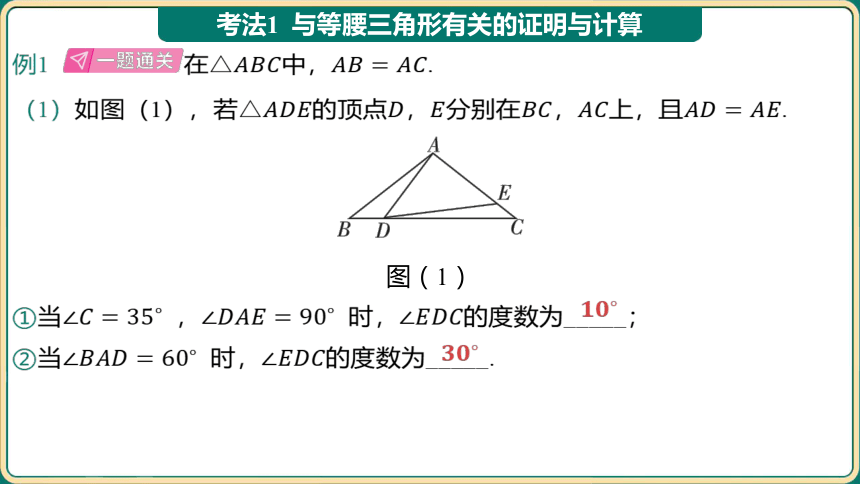
考法1 与等腰三角形有关的证明与计算
例1 在中, .
(1)如图(1),若的顶点,分别在,上,且 .
图(1)
①当 , 时, 的度数为_____;
②当 时, 的度数为_____.
图(2)
(2)如图(2),若,该三角形的面积为15,点
是边上任意一点,则点到,边的距离之和 的
值为___.
5
图(3)
(3)如图(3),若, ,点在 上,且
,点为的中点,连接,则的长为____,
的周长为_________.
(4)如图(4),是边的中点,连接,平分交于点 ,过
点作交于点 .
图(4)
①若 ,则____ ;
②若,则 的长为___.
54
4
图(5)
(5)如图(5),若是边上一点, ,将
沿翻折,点的对应点为点,连接,当
是以为底边的等腰三角形时, 的度数为________
___.
或
[解析] 解法提示:, , .分两种情况讨论.
①当,且点在下方时,如图(1),设 ,则
, .又 ,
, , .
根据,可得 , .
图(1)
②当,且点在上方时,如图(2),设 ,则
, , ,
.根据,可得 ,
.
图(2)
考法2 与直角三角形有关的证明与计算
例2 在中, .
(1)当点为 的中点时,
①连接,若 ,则____ .
②如图(1),若 ,,于点,则 的长为___.
55
1
图(1)
图(2)
③如图(2),若 ,点是 边的中点,连接,,是
中边上的中线, ,则 的长为_ __.
④如图(3),过点作,垂足为,若,,则
的长为_ ___.
图(3)
考法2 与直角三角形有关的证明与计算
[解析] 解法提示:
方法一:在中, ,,, 由勾股定
理得是 的中点,
.设 ,由勾股定理得
,解得, .
方法二:的面积.是 的中
点,的面积的面积. 在 中,
, ,, 由勾股定理得
, ,
.
(2)如图(4),若,,点在边上,将沿 折叠得到
,与边交于点.若为直角三角形,则 的长是______.
2或5
图(4)
解题指导
(2)当
[解析] 解法提示:根据题意,易得.由折叠的性质可得 ,
.由题意知,可分两种情况讨论.①如图(1),当
时,过点作交的延长线于点,则四边形
为矩形.设,则,.在
中,,即,解得,
(舍去),.②如图(2),当 时,点与点 重合.
,,.设,则 .在
中,,即,解得 ,
.综上, 的长为2或5.
图(1)
图(2)
命题点1 与等腰三角形有关的证明与计算[8年6
考]
(第1题)
1.[2020福建中考,5] 如图,是等腰三角形 的顶角
平分线,,则 等于( )
B
A.10 B.5 C.4 D.3
(第2题)
2.[2024龙岩质检] 如图,中,,
于点,点是的中点,连接 ,则下列结论不一定
正确的是( )
A
A. B.
C. D.
命题点2 与等边三角形有关的证明与计算[8年4
考]
(第3题)
3.[2018福建中考,5] 如图,等边三角形中, ,垂
足为点,点在线段上, ,则 等于
( )
A
A. B.
C. D.
4.[2023南平质检] 在等边三角形中,点,分别是边, 的中点,
若的周长为12,则 的周长为( )
C
A.3 B.4 C.6 D.9
5.[2024宁德质检] 如图,在等边三角形中,为的中点, 于
点,,则 的长是____.
20
(第5题)
6.[2023三明质检] 如图,为等边三角形,点在 边上.
(1)在内部求作点,使得是以 为底边的等腰直角三角形;
(尺规作图,保留作图痕迹,不写作法)
[答案] 如图(1),点 即为所求作的点.
图(1)
(2)在(1)的条件下,连接,,延长交于点,若 ,求证:
.
图(2)
证明:如图(2),
为等边三角形, 为等腰直角三角形,
, , ,
,
.
, ,
,
,
.
,
,
,
.
图(2)
命题点3 与直角三角形有关的计算[8年6考]
7.[2024宁德质检] 在中, ,,,则 的
长是( )
C
A. B.11 C.13 D.17
(第8题)
8.[2022泉州质检] 如图,在矩形中,点在边 上,点
是的中点,,,则 的长为
( )
C
A. B. C. D.
(第9题)
9.[2024漳州质检] 如图,在和 中,
,,相交于点,,分别是 ,
的中点,连接,,.若点为 的内心,
,则下面结论错误的是( )
D
A. B.
C. D.
新课标 新考向
【新课标·项目式学习】[2024滨州中考] 【问题背景】
某校八年级数学社团在研究等腰三角形“三线合一”性质时发现:
①如图,在中,若,,则有 ;
②某同学顺势提出一个问题:既然①正确,那么进一步推得 ,即知
.若把①中的替换为 ,还
能推出 吗?
基于此,社团成员小军、小民进行了探索研究,发现确实能推出 ,
并分别提供了不同的证明方法.
小军
证明:分别延长,至, 两点,使得……
小民
证明: ,
与 均为直角三角形,
根据勾股定理,得……
【问题解决】
备用图
(1)完成①的证明;
证明: ,
.
在和中,
,
.
(2)把②中小军、小民的证明过程补充完整.
[答案] 补充完整小军的证明过程如下:
分别延长,至,两点,使得, ,如图所示.
,
,即 .
, .
在和中,
, .
, ,
, .
又, ,
.
补充完整小民的证明过程如下:
,与 均为直角三角
形,
根据勾股定理,得 ,
,
,
.
,
,
,
,
,
.
又 ,
,
.
第四章 三角形
第一部分 中考考点梳理
第四节 等腰三角形与直角三角形
2025年中考数学一轮复习
考点梳理
1.等腰三角形和等边三角形[重点]
等腰三角形 等边三角形
性质 (1)两腰相等,两底角 ①______; (2)顶角平分线、底边上的中 线、底边上的高互相重合 (简写成“三线合一”); (3)是轴对称图形,有②____ 条对称轴. (1)三边都相等,三个内角都相
等,且都等于③_____;
(2)每条边上的中线、该边上的
高和该边所对角的平分线互相重
合;
(3)是轴对称图形,有④____条对
称轴.
相等
一
三
等腰三角形 等边三角形
判定 (1)有两条边相等的三角形是 等腰三角形. (2)有两个角相等的三角形是 等腰三角形. (1)三边都相等的三角形是等边
三角形.
(2)三个内角都相等的三角形是
等边三角形.
(3)有一个内角等于 的等腰
三角形是等边三角形.
面积 (为底边 上的高). (为任意边 上
的高).
【易失分点】 解决与等腰三角形有关的问题时的易错点
①已知等腰三角形的一个角,求其他角的度数时,要对该角是顶角还是底角
进行分类讨论.
②求等腰三角形的一条边:当已知等腰三角形的两边时,除了要确定哪条边
作为腰或底边外,还要判断是否满足三角形的三边关系.
回练课本
1.(1)如图(1),为等边三角形,延长到点,使 .延
长到点,使.连接,,则 的度数是( )
图(1)
B
A. B. C. D.
(2)用一条长为的细绳围成一个等腰三角形,若有一边长为 ,则
这个等腰三角形的腰长为( )
D
A. B. C.或 D.
图(2)
(3)如图(2),在 中,按以下步骤作图:
①以点为圆心,以适当长为半径作弧分别交 ,
于,两点;②分别以点, 为圆心,大于
的长为半径作弧,两弧交于点;③作射线
3
交于点,过点作交的延长线于点.若, ,
则 ___.
2.直角三角形[重点]
直角三角形 等腰直角三角形
性质 (1)两锐角互余; (2)斜边上的中线等于斜边的一半; 角所对的直角边等于斜边的一 半; (4)勾股定理:直角三角形中两直角边 的平方和等于斜边的平方,即 (,为直角边, 为斜 边). (1)两直角边相等;
(2)两锐角相等且都等
于 ;
(3)是轴对称图形,有
一条对称轴.
直角三角形 等腰直角三角形
判定 (1)有一个角为 的三角形是 直角三角形; (2)勾股定理的逆定理:若三角 形的三边长,, 满足 ,则该三角形是直角 三角形. 【拓展】 如果三角形的一边上的 中线等于这条边的一半,那么这 个三角形是直角三角形. (1)顶角为 的等腰三角
形是等腰直角三角形;
(2)有两个角是 的三角
形是等腰直角三角形;
(3)有一个角是 的直角
三角形是等腰直角三角形;
(4)两直角边相等的直角三
角形是等腰直角三角形.
直角三角形 等腰直角三角形
面积 (, 为直角边, 为斜边, 为斜边上的高). ( 为直角边,
为斜边, 为斜边上的高).
【解题通法】 解与直角三角形有关的计算题的常用思路
①当出现
②当出现斜边上的中线时,要想到直角三角形中斜边上的中线等于斜边的一半.
③作辅助线构造直角三角形,利用勾股定理或三角函数求线段长或角度.
④已知直角三角形的三边求斜边上的高时,用面积法求解.
⑤已知三角形为直角三角形,但没有明确直角顶点,则需要分类讨论.
图(1)
2.(1)如图(1),已知,边的长为4,以 为
边作正方形,设面积为.以为边作正方形 ,
设面积为.则 的值为____.
16
图(2)
(2)如图(2),点在的边上,点是 的
中点,连接,,若,, ,
,则 的长为____.
回练课本
图(3)
(3)如图(3),在中,是 边上的点,
,,分别是,边的中点,若,则
的长为___.
3
图(4)
(4)如图(4),已知 ,点在边 上,
,点,在边上,.若 ,则
的周长是____.
16
考法1 与等腰三角形有关的证明与计算
例1 在中, .
(1)如图(1),若的顶点,分别在,上,且 .
图(1)
①当 , 时, 的度数为_____;
②当 时, 的度数为_____.
图(2)
(2)如图(2),若,该三角形的面积为15,点
是边上任意一点,则点到,边的距离之和 的
值为___.
5
图(3)
(3)如图(3),若, ,点在 上,且
,点为的中点,连接,则的长为____,
的周长为_________.
(4)如图(4),是边的中点,连接,平分交于点 ,过
点作交于点 .
图(4)
①若 ,则____ ;
②若,则 的长为___.
54
4
图(5)
(5)如图(5),若是边上一点, ,将
沿翻折,点的对应点为点,连接,当
是以为底边的等腰三角形时, 的度数为________
___.
或
[解析] 解法提示:, , .分两种情况讨论.
①当,且点在下方时,如图(1),设 ,则
, .又 ,
, , .
根据,可得 , .
图(1)
②当,且点在上方时,如图(2),设 ,则
, , ,
.根据,可得 ,
.
图(2)
考法2 与直角三角形有关的证明与计算
例2 在中, .
(1)当点为 的中点时,
①连接,若 ,则____ .
②如图(1),若 ,,于点,则 的长为___.
55
1
图(1)
图(2)
③如图(2),若 ,点是 边的中点,连接,,是
中边上的中线, ,则 的长为_ __.
④如图(3),过点作,垂足为,若,,则
的长为_ ___.
图(3)
考法2 与直角三角形有关的证明与计算
[解析] 解法提示:
方法一:在中, ,,, 由勾股定
理得是 的中点,
.设 ,由勾股定理得
,解得, .
方法二:的面积.是 的中
点,的面积的面积. 在 中,
, ,, 由勾股定理得
, ,
.
(2)如图(4),若,,点在边上,将沿 折叠得到
,与边交于点.若为直角三角形,则 的长是______.
2或5
图(4)
解题指导
(2)当
[解析] 解法提示:根据题意,易得.由折叠的性质可得 ,
.由题意知,可分两种情况讨论.①如图(1),当
时,过点作交的延长线于点,则四边形
为矩形.设,则,.在
中,,即,解得,
(舍去),.②如图(2),当 时,点与点 重合.
,,.设,则 .在
中,,即,解得 ,
.综上, 的长为2或5.
图(1)
图(2)
命题点1 与等腰三角形有关的证明与计算[8年6
考]
(第1题)
1.[2020福建中考,5] 如图,是等腰三角形 的顶角
平分线,,则 等于( )
B
A.10 B.5 C.4 D.3
(第2题)
2.[2024龙岩质检] 如图,中,,
于点,点是的中点,连接 ,则下列结论不一定
正确的是( )
A
A. B.
C. D.
命题点2 与等边三角形有关的证明与计算[8年4
考]
(第3题)
3.[2018福建中考,5] 如图,等边三角形中, ,垂
足为点,点在线段上, ,则 等于
( )
A
A. B.
C. D.
4.[2023南平质检] 在等边三角形中,点,分别是边, 的中点,
若的周长为12,则 的周长为( )
C
A.3 B.4 C.6 D.9
5.[2024宁德质检] 如图,在等边三角形中,为的中点, 于
点,,则 的长是____.
20
(第5题)
6.[2023三明质检] 如图,为等边三角形,点在 边上.
(1)在内部求作点,使得是以 为底边的等腰直角三角形;
(尺规作图,保留作图痕迹,不写作法)
[答案] 如图(1),点 即为所求作的点.
图(1)
(2)在(1)的条件下,连接,,延长交于点,若 ,求证:
.
图(2)
证明:如图(2),
为等边三角形, 为等腰直角三角形,
, , ,
,
.
, ,
,
,
.
,
,
,
.
图(2)
命题点3 与直角三角形有关的计算[8年6考]
7.[2024宁德质检] 在中, ,,,则 的
长是( )
C
A. B.11 C.13 D.17
(第8题)
8.[2022泉州质检] 如图,在矩形中,点在边 上,点
是的中点,,,则 的长为
( )
C
A. B. C. D.
(第9题)
9.[2024漳州质检] 如图,在和 中,
,,相交于点,,分别是 ,
的中点,连接,,.若点为 的内心,
,则下面结论错误的是( )
D
A. B.
C. D.
新课标 新考向
【新课标·项目式学习】[2024滨州中考] 【问题背景】
某校八年级数学社团在研究等腰三角形“三线合一”性质时发现:
①如图,在中,若,,则有 ;
②某同学顺势提出一个问题:既然①正确,那么进一步推得 ,即知
.若把①中的替换为 ,还
能推出 吗?
基于此,社团成员小军、小民进行了探索研究,发现确实能推出 ,
并分别提供了不同的证明方法.
小军
证明:分别延长,至, 两点,使得……
小民
证明: ,
与 均为直角三角形,
根据勾股定理,得……
【问题解决】
备用图
(1)完成①的证明;
证明: ,
.
在和中,
,
.
(2)把②中小军、小民的证明过程补充完整.
[答案] 补充完整小军的证明过程如下:
分别延长,至,两点,使得, ,如图所示.
,
,即 .
, .
在和中,
, .
, ,
, .
又, ,
.
补充完整小民的证明过程如下:
,与 均为直角三角
形,
根据勾股定理,得 ,
,
,
.
,
,
,
,
,
.
又 ,
,
.
同课章节目录
