2025年中考数学一轮复习 -第四章 三角形-第六节 锐角三角函数及其应用 课件(共33张PPT)
文档属性
| 名称 | 2025年中考数学一轮复习 -第四章 三角形-第六节 锐角三角函数及其应用 课件(共33张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 00:00:00 | ||
图片预览









文档简介
(共33张PPT)
第四章 三角形
第一部分 中考考点梳理
第六节 锐角三角函数及其应用
2025年中考数学一轮复习
考点梳理
1.锐角三角函数[基础点]
如图,在
角,
的正弦: .
的余弦: .
的正切: .
回练课本
1.在中, ,,,分别为,, 的对边,下列各式
成立的是( )
B
A. B. C. D.
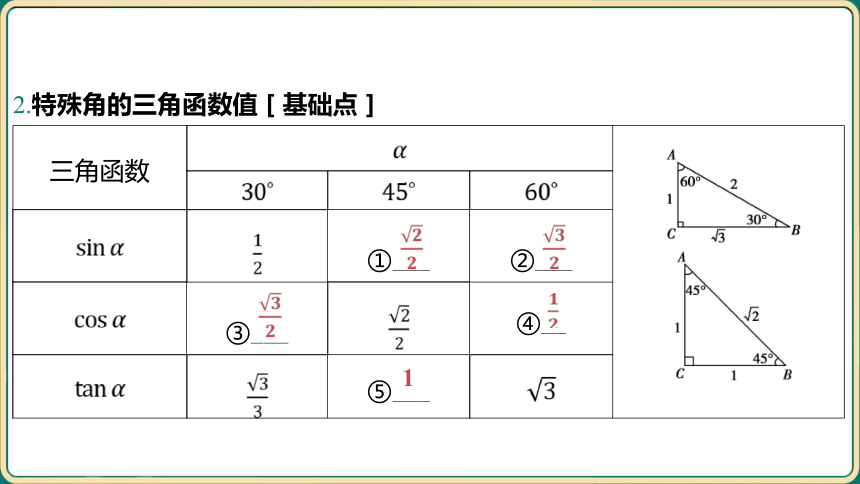
2.特殊角的三角函数值[基础点]
三角函数 ________________________________________
_______________________________________
①_ __ ②_ __ ③_ __ ④__ ⑤___
1
2.计算:
(1) .
[答案] 原式
.
(2) .
[答案] 原式
.
回练课本
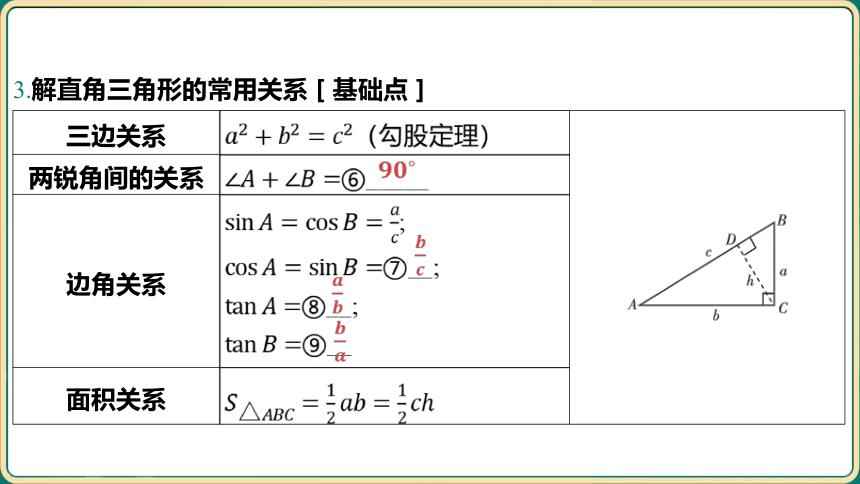
3.解直角三角形的常用关系[基础点]
三边关系 (勾股定理) ___________________________________________
两锐角间的关系 ⑥_____ 边角关系 ; ⑦__; ⑧__; ⑨__ 面积关系
3.已知在中,,,分别是,, 的对边.
(1)若 ,,,则 的度数为_____.
(2)若 ,,,则 的值为_____.
回练课本
4.锐角三角函数的实际应用[重点]
(1)仰角、俯角:如图,在同一铅垂面内视线和水平线的
夹角中,视线在水平线上方的是仰角,视线在水平线下方
的是俯角.
(2)坡度(坡比)、坡角:如图,坡面的垂直高度 和水
平宽度的比叫坡度(坡比),记作,即 ;坡面与水
平线的夹角 叫坡角,则 .
(3)方位角:一般指以观测者的位置为中心,将正北或
正南方向线作为起始方向,旋转到目标的方向线所成的角
(一般指锐角),通常表达成北(或南)偏东(或西).
如图,点在点的北偏西 的方向,点在点 的北偏东
的方向(或东北方向),点在点的南偏西 的方向.
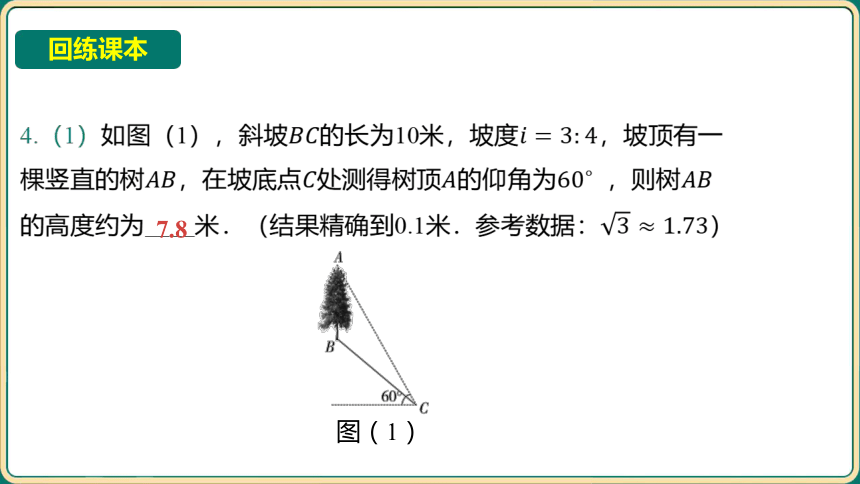
图(1)
4.(1)如图(1),斜坡的长为10米,坡度 ,坡顶有一
棵竖直的树,在坡底点处测得树顶的仰角为 ,则树
的高度约为____米.(结果精确到0.1米.参考数据: )
7.8
回练课本
(2)如图(2),海中有一个小岛.一艘轮船由西向东航行,在 点测得小
岛在北偏东 方向上;航行到达点,这时测得小岛 在北偏东
方向上.小岛到航线的距离是_____ ,结果精确到
.
10.4
图(2)
考法 锐角三角函数的实际应用
例1 [2024江西中考] 图(1)是世界第一“大碗”——景德镇昌南里文化艺术
中心主体建筑,其造型灵感来自宋代湖田窑影青斗笠碗,寓意“万瓷之母”.如图
(2),“大碗”的主视图由“大碗”主体和矩形碗底 组成.已知
,,是太阳光线,,,点,,, 在同一条直线上.
经测量,,,, .
(结果精确到 )
图(1)
图(2)
(1)求“大碗”的口径 的长;
[答案] , ,
.
又 ,
四边形 是平行四边形,
.
, ,
,
,
即“大碗”的口径为 .
(2)求“大碗”的高度 的长.
(参考数据:,, )
[答案] 如图,过点作于点 ,则
.
四边形 是矩形,
,
.
,
,
四边形 是矩形,
,, .
,
,
,
,
即“大碗”的高度约为 .
例2 [2024广东中考] 中国新能源汽车为全
球应对气候变化和绿色低碳转型作出了巨大
贡献.为满足新能源汽车的充电需求,某小区
增设了充电站,如图是矩形充电站的平面示意图,矩形 是其中一个
停车位.经测量, ,,, , 是另一个
车位的宽,所有车位的长宽相同,按图示并列划定.
根据以上信息回答下列问题:(结果精确到,参考数据: )
(1)求 的长;
[答案] 四边形, 是矩形,
, .
又 ,
,
.
在中, ,
.
在中, ,
.
在中, ,
,
.
(2)该充电站有20个停车位,求 的长.
[答案] 在中, ,
.
在中, ,
,
.
图(1)
例3 [2024苏州中考] 图(1)是某种可调节支撑架, 为水平
固定杆,竖直固定杆,活动杆可绕点旋转, 为液
压可伸缩支撑杆,已知,, .
(1)如图(2),当活动杆处于水平状态时,求可伸缩支撑杆 的长度
(结果保留根号);
图(2)
[答案] 如图(1),过点作,垂足为 .
由题意可知, .
又, 四边形 为矩形.
,,, .
, ,
在中, .
可伸缩支撑杆的长度为 .
图(1)
(2)如图(3),若活动杆绕点由水平状态按逆时针方向旋转角度 ,且
( 为锐角),求此时可伸缩支撑杆 的长度(结果保留根号).
图(3)
图(2)
[答案] 如图(2),过点作,交 的延长线于
点,交于点 .
由题意可知,四边形为矩形, .
在中,, ,
.
,, ,
, ,
, ,
在 中,
.
此时可伸缩支撑杆的长度为 .
命题点 锐角三角函数的实际应用[8年4考]
(第1题)
1.[2021福建中考,3] 如图,某研究性学习小组为测量学
校与河对岸工厂之间的距离,在学校附近选一点 ,利
用测量仪器测得 , , .据此,
可求得学校与工厂之间的距离 等于( )
D
A. B. C. D.
(第2题)
2.[2022福建中考,9] 如图所示的衣架可以近似看成一
个等腰三角形,其中, ,
,则高约为(参考数据: ,
, )( )
B
A. B. C. D.
(第3题)
3.[2023宁德质检] 如图是某商场营业大厅自动扶梯示意
图.自动扶梯的长为,倾斜角为 ,则自动扶梯
的垂直高度 等于( )
C
A. B.
C. D.
4.[2024福建中考,16] 无动力帆船是借助风力前行的.如图
是帆船借助风力航行的平面示意图,已知帆船航行方向与
风向所在直线的夹角为 ,帆与航行方向的夹角
为 ,风对帆的作用力为.根据物理知识,
128
可以分解为两个力与,其中与帆平行的力不起作用,与帆垂直的力 又
可以分解为两个力与,与航行方向垂直,被舵的阻力抵消; 与航行方
向一致,是真正推动帆船前行的动力.在物理学上常用线段的长度表示力的大
小,据此,建立数学模型:,则_____. (单位: )
(参考数据:, )
5.[2024厦门质检] 为创造美丽环境,某社区将辖区内一四边形闲置区域改造
为一个生态景观区,平面示意图如图所示.景观区建有一个四叶草形生态水
池及一座雕塑,水池内点处建有观景台,, 是两条通往观景台的步
行道,其中步行道与边 垂直,四边形内其他区域铺设草坪.观景台上
安装了一盏广角灯,四边形 是广角灯夜间开启时灯光所覆盖的区
域.小梧从该社区了解到,为了凸显景观的层次感和立体感,达到理想的光
影效果,对该广角灯的要求是:照射角为 .他想验证该广角灯是
否符合要求,于是利用身边仅有的一个卷尺根据现场条件进行测量,所得数
据如下表所示.
备用图
所测的量
长度/ 15.00 15.00 17.32 17.32 6.00 24.00
(1)步行道与边 是否也垂直?请说明理由.
[答案] 与 也垂直.
理由:如图,连接 ,
由测量数据可知, .
.
又, ,
.
.
.
(2)根据所测得的数据,小梧能否完成验证?若能,请帮小梧完成验证;
若不能,请说明理由.(参考数据: )
[答案] 小梧可以完成验证,过程如下:
如图,过点作,垂足为点 .
在中,, ,
,
.
.
在中, , ,
, .
.
在与中, ,且
,
,
.
.
即 .
由(1)可知, ,
.
故该广角灯符合要求.
第四章 三角形
第一部分 中考考点梳理
第六节 锐角三角函数及其应用
2025年中考数学一轮复习
考点梳理
1.锐角三角函数[基础点]
如图,在
角,
的正弦: .
的余弦: .
的正切: .
回练课本
1.在中, ,,,分别为,, 的对边,下列各式
成立的是( )
B
A. B. C. D.
2.特殊角的三角函数值[基础点]
三角函数 ________________________________________
_______________________________________
①_ __ ②_ __ ③_ __ ④__ ⑤___
1
2.计算:
(1) .
[答案] 原式
.
(2) .
[答案] 原式
.
回练课本
3.解直角三角形的常用关系[基础点]
三边关系 (勾股定理) ___________________________________________
两锐角间的关系 ⑥_____ 边角关系 ; ⑦__; ⑧__; ⑨__ 面积关系
3.已知在中,,,分别是,, 的对边.
(1)若 ,,,则 的度数为_____.
(2)若 ,,,则 的值为_____.
回练课本
4.锐角三角函数的实际应用[重点]
(1)仰角、俯角:如图,在同一铅垂面内视线和水平线的
夹角中,视线在水平线上方的是仰角,视线在水平线下方
的是俯角.
(2)坡度(坡比)、坡角:如图,坡面的垂直高度 和水
平宽度的比叫坡度(坡比),记作,即 ;坡面与水
平线的夹角 叫坡角,则 .
(3)方位角:一般指以观测者的位置为中心,将正北或
正南方向线作为起始方向,旋转到目标的方向线所成的角
(一般指锐角),通常表达成北(或南)偏东(或西).
如图,点在点的北偏西 的方向,点在点 的北偏东
的方向(或东北方向),点在点的南偏西 的方向.
图(1)
4.(1)如图(1),斜坡的长为10米,坡度 ,坡顶有一
棵竖直的树,在坡底点处测得树顶的仰角为 ,则树
的高度约为____米.(结果精确到0.1米.参考数据: )
7.8
回练课本
(2)如图(2),海中有一个小岛.一艘轮船由西向东航行,在 点测得小
岛在北偏东 方向上;航行到达点,这时测得小岛 在北偏东
方向上.小岛到航线的距离是_____ ,结果精确到
.
10.4
图(2)
考法 锐角三角函数的实际应用
例1 [2024江西中考] 图(1)是世界第一“大碗”——景德镇昌南里文化艺术
中心主体建筑,其造型灵感来自宋代湖田窑影青斗笠碗,寓意“万瓷之母”.如图
(2),“大碗”的主视图由“大碗”主体和矩形碗底 组成.已知
,,是太阳光线,,,点,,, 在同一条直线上.
经测量,,,, .
(结果精确到 )
图(1)
图(2)
(1)求“大碗”的口径 的长;
[答案] , ,
.
又 ,
四边形 是平行四边形,
.
, ,
,
,
即“大碗”的口径为 .
(2)求“大碗”的高度 的长.
(参考数据:,, )
[答案] 如图,过点作于点 ,则
.
四边形 是矩形,
,
.
,
,
四边形 是矩形,
,, .
,
,
,
,
即“大碗”的高度约为 .
例2 [2024广东中考] 中国新能源汽车为全
球应对气候变化和绿色低碳转型作出了巨大
贡献.为满足新能源汽车的充电需求,某小区
增设了充电站,如图是矩形充电站的平面示意图,矩形 是其中一个
停车位.经测量, ,,, , 是另一个
车位的宽,所有车位的长宽相同,按图示并列划定.
根据以上信息回答下列问题:(结果精确到,参考数据: )
(1)求 的长;
[答案] 四边形, 是矩形,
, .
又 ,
,
.
在中, ,
.
在中, ,
.
在中, ,
,
.
(2)该充电站有20个停车位,求 的长.
[答案] 在中, ,
.
在中, ,
,
.
图(1)
例3 [2024苏州中考] 图(1)是某种可调节支撑架, 为水平
固定杆,竖直固定杆,活动杆可绕点旋转, 为液
压可伸缩支撑杆,已知,, .
(1)如图(2),当活动杆处于水平状态时,求可伸缩支撑杆 的长度
(结果保留根号);
图(2)
[答案] 如图(1),过点作,垂足为 .
由题意可知, .
又, 四边形 为矩形.
,,, .
, ,
在中, .
可伸缩支撑杆的长度为 .
图(1)
(2)如图(3),若活动杆绕点由水平状态按逆时针方向旋转角度 ,且
( 为锐角),求此时可伸缩支撑杆 的长度(结果保留根号).
图(3)
图(2)
[答案] 如图(2),过点作,交 的延长线于
点,交于点 .
由题意可知,四边形为矩形, .
在中,, ,
.
,, ,
, ,
, ,
在 中,
.
此时可伸缩支撑杆的长度为 .
命题点 锐角三角函数的实际应用[8年4考]
(第1题)
1.[2021福建中考,3] 如图,某研究性学习小组为测量学
校与河对岸工厂之间的距离,在学校附近选一点 ,利
用测量仪器测得 , , .据此,
可求得学校与工厂之间的距离 等于( )
D
A. B. C. D.
(第2题)
2.[2022福建中考,9] 如图所示的衣架可以近似看成一
个等腰三角形,其中, ,
,则高约为(参考数据: ,
, )( )
B
A. B. C. D.
(第3题)
3.[2023宁德质检] 如图是某商场营业大厅自动扶梯示意
图.自动扶梯的长为,倾斜角为 ,则自动扶梯
的垂直高度 等于( )
C
A. B.
C. D.
4.[2024福建中考,16] 无动力帆船是借助风力前行的.如图
是帆船借助风力航行的平面示意图,已知帆船航行方向与
风向所在直线的夹角为 ,帆与航行方向的夹角
为 ,风对帆的作用力为.根据物理知识,
128
可以分解为两个力与,其中与帆平行的力不起作用,与帆垂直的力 又
可以分解为两个力与,与航行方向垂直,被舵的阻力抵消; 与航行方
向一致,是真正推动帆船前行的动力.在物理学上常用线段的长度表示力的大
小,据此,建立数学模型:,则_____. (单位: )
(参考数据:, )
5.[2024厦门质检] 为创造美丽环境,某社区将辖区内一四边形闲置区域改造
为一个生态景观区,平面示意图如图所示.景观区建有一个四叶草形生态水
池及一座雕塑,水池内点处建有观景台,, 是两条通往观景台的步
行道,其中步行道与边 垂直,四边形内其他区域铺设草坪.观景台上
安装了一盏广角灯,四边形 是广角灯夜间开启时灯光所覆盖的区
域.小梧从该社区了解到,为了凸显景观的层次感和立体感,达到理想的光
影效果,对该广角灯的要求是:照射角为 .他想验证该广角灯是
否符合要求,于是利用身边仅有的一个卷尺根据现场条件进行测量,所得数
据如下表所示.
备用图
所测的量
长度/ 15.00 15.00 17.32 17.32 6.00 24.00
(1)步行道与边 是否也垂直?请说明理由.
[答案] 与 也垂直.
理由:如图,连接 ,
由测量数据可知, .
.
又, ,
.
.
.
(2)根据所测得的数据,小梧能否完成验证?若能,请帮小梧完成验证;
若不能,请说明理由.(参考数据: )
[答案] 小梧可以完成验证,过程如下:
如图,过点作,垂足为点 .
在中,, ,
,
.
.
在中, , ,
, .
.
在与中, ,且
,
,
.
.
即 .
由(1)可知, ,
.
故该广角灯符合要求.
同课章节目录
