2025年中考数学一轮复习 -第五章 四边形-第一节 平行四边形与多边形 课件(共41张PPT)
文档属性
| 名称 | 2025年中考数学一轮复习 -第五章 四边形-第一节 平行四边形与多边形 课件(共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 13:21:53 | ||
图片预览









文档简介
(共41张PPT)
第五章 四边形
第一部分 中考考点梳理
第一节 平行四边形与多边形
2025年中考数学一轮复习
考点梳理
1.平行四边形的性质与判定[重点]
(1)定义:两组对边①__________的四边形叫做平行四边形.
(2)性质与判定
分别平行
图形 元素 性质 判定 文字语言 符号表示
__________________________________ 边 两组对边 分别平行. 两组对边分别② ______的四边形 是平行四边形. (定义法) 四边形
是平行四边形.
平行
图形 元素 性质 判定 文字语言 符号表示
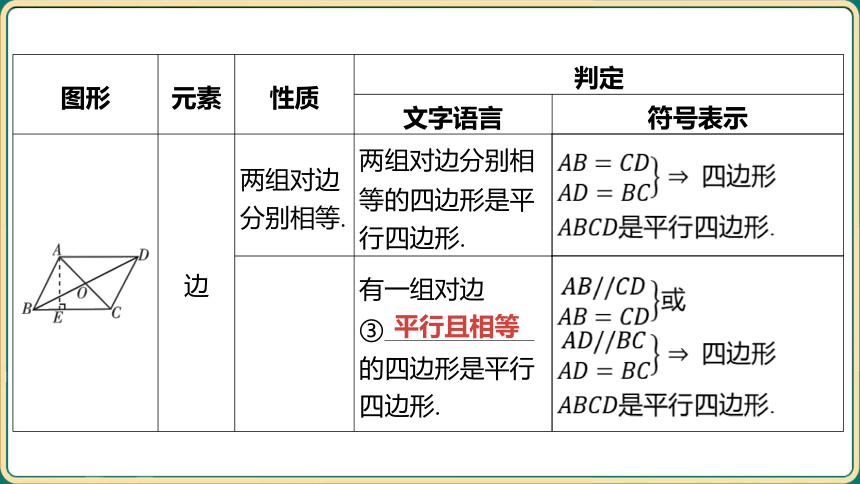
__________________________________ 边 两组对边 分别相等. 两组对边分别相 等的四边形是平 行四边形. 四边形
是平行四边形.
有一组对边 ③____________ 的四边形是平行 四边形. 或
四边形
是平行四边形.
平行且相等
图形 元素 性质 判定 文字语言 符号表示
__________________________________ 角 两组对角 分别相等. 两组对角分别④ ______ 的四边 形是平行四边形. 四边
形 是平行四边形.
邻角互补. 对角线 对角线互 相平分. 对角线互相 ⑤______的四边 形是平行四边形. 四边形
是平行四边形.
相等
平分
(3)平行四边形的对称性:平行四边形是中心对称图形,两条对角线的交点
是它的对称中心.
(4)平行四边形(如上表格中的图)的面积: ⑥____
.
【易失分点】 与平行四边形的证明和计算有关的常见误区
①注意平行四边形的面积公式不要与三角形的面积公式相混淆.
②一组对边平行,另一组对边相等的四边形不一定是平行四边形,可能是等腰梯形.
③平行四边形不是轴对称图形.
【提分指南】①平行四边形两个邻角的平分线互相垂直,两个对角的平分线
互相平行(或共线).
②平行四边形被任意一条对角线分成面积相等的两个三角形,被两条对角线
分成面积相等的四个三角形;过平行四边形对角线交点的任意一条直线平分
平行四边形的面积.
③当平行四边形中有角平分线的条件时,可利用“平行角平分线 等腰三
角形”的结论得到等角等边,如图(1).
图(1)
④当平行四边形中存在边上的中点时,连接该中点与对角线的交点可得到三
角形的中位线,如图(2).
图(2)
回练课本
图(1)
1.(1)如图(1),在四边形中, .添加下列
条件后,仍不能判定该四边形 为平行四边形的是( )
D
A. B. C. D.
图(2)
(2)如图(2),两张对边平行的纸条,随意交叉叠放在一起,
重合的阴影部分构成了一个四边形,转动其中一张纸条,则下
列结论一定成立的是( )
B
A. B.
C. D.
(3)在平面直角坐标系中,若以,, 三点为顶点画
平行四边形,则第四个顶点不可能在( )
C
A.第一象限 B.第二象限 C.第三象限 D.第四象限
图(3)
(4)如图(3),四边形 是平行四边形,
,平分且交于点,且交 于
点,则 的大小为_____.
图(4)
(5)已知四边形是平行四边形,如图(4),若 平
分, ,则 的度数为______.
(6)如图(5),, 是两条平行线,则平行四边形甲、乙的面积关系是:
___.(填“ ”“ ”或“ ”)
图(5)
2.多边形[重点]
(1)与多边形有关的计算
边形 ( , 且 为整 数) 内角和定理 边形的内角和为 .
外角和定理 边形的外角和为⑦______.
对角线 过边形的一个顶点可引出 条对
角线;边形共有 条对角线.
(2)正多边形及其性质
正 边形 ( , 且 为整 数) 边、角 正多边形的各边相等,各角相等.
内角、 外角 每一个内角的度数为 ,每一个外角的度数为
.
正 边形 ( , 且 为整 数) 对称性 (1)正边形有 条对称轴;
(2)当为奇数时,正 边形是轴对称图形,但不是
中心对称图形;当为偶数时,正 边形既是轴对称图
形,又是中心对称图形.
(3)正 边形有一个外接圆和一个内切圆,它们是同心
圆.
【注意】 每条边都相等的多边形不一定是正多边形,因为它的内角不一定都
相等,如菱形;每个内角都相等的多边形也不一定是正多边形,因为它的边不一
定相等,如矩形.
2.(1)若正多边形的一个外角的度数为 ,则这个正多边形的边数为___.
(2)正多边形一个内角的度数是 ,则该正多边形的边数是____.
(3)如图,在正六边形中,连接,相交于点,则
______.
8
12
回练课本
考法1 平行四边形的性质与判定
例1 如图,在中,点,,分别为 ,
,边上的点,与相交于点 .
(1)当 时,添加一个条件:______________________
__________,使得四边形 为平行四边形.
答案不唯一,如或
(2)当 时,添加一个条件:_______________________________
________________,使得四边形 为平行四边形.
(3)当 时,添加一个条件:_________________________________
______________________,使得四边形 为平行四边形.
答案不唯一,如,或
答案不唯一,如,或
解题通法
平行四边形的判定思路
证这组对边平行;
证另一组对边相等.
证这组对边相等;
证另一组对边平行.
证另一组对角相等;
证一组对边平行.
4.已知一条对角线平分另一条对角线,证对角线互相平分.
1.已知一组对边相等
2.已知一组对边平行
3.已知一组对角相等
例2 已知四边形 是平行四边形.
图(1)
(1)如图(1),若点是边的中点,点 为对角线的交
点,的周长为6,则 的周长为____.
12
图(2)
(2)如图(2),于点,若 ,
,,则 的周长为__________.
(3)如图(3),,相交于点,,, .
图(3)
①的面积为_____, 的面积为_ ___;
②的长为_ __, 的长为_____;
③若点是的中点,连接交于点,则 的长为_ ___.
解法提示:,, ,
.又, .
解题通法
利用平行四边形的性质进行相关计算的方法
1.求角度:先将题中的已知角找出来,再结合平行四边形的性质(即对角相等,
邻角互补及对边平行),将所求角与已知角联系起来.
2.求线段长:
(1)根据平行四边形的性质将已知条件转化到一个三角形中,利用勾股定
理、直角三角形的性质、等腰三角形的性质、三角函数或三角形面积公式等
进行求解;
(2)根据平行四边形的性质,利用中位线定理、平行线分线段成比例、全
等三角形的判定与性质或相似三角形的判定与性质等进行求解.
考法2 多边形的相关计算
例3 已知一个 边形.
(1)若 ,则它的内角和为______,外角和为______.
(2)若它的每一个内角都为 ,则___;若它的每一个外角都为 ,
则 ___.
(3)如图(1),在正五边形中, 的度数为_____.
8
9
图(1)
(4)①如图(2),在正六边形中,若,则 的长为____;
图(2)
图(3)
②如图(3),点为正六边形对角线 上一点,
,,则 的值是____.
30
[解析] 解法提示:如图(1),连接,易知四边形
为矩形,, ,
, .如图(2),正六边形
被分割成6个面积相等的三角形,可知每个三角形的面积均为
, .
图(1)
图(2)
命题点1 平行四边形的性质[8年3考]
1.[2024宁德质检] 如图,在中, ,则 的度数是( )
B
(第1题)
A. B. C. D.
(第2题)
2.[2023福建中考,12] 如图,在中, 为
的中点,过点且分别交,于点, .若
,则 的长为____.
10
3.[2022三明质检] 已知:如图,在中,为的中点, 于
点,于点 .
求证:
(1) ;
证明: 四边形 为平行四边形,
, .
, ,
,
,
,
.
(2)为 的中点.
[答案] 证法一:如图(1),延长交于点 ,
图(1)
四边形 为平行四边形,
, .
, ,
,
,
四边形 为平行四边形,
图(1)
.
为的中点, ,
.
, ,
,即为 的中点.
图(1)
证法二:如图(2),延长,交于点 .
图(2)
四边形 为平行四边形,
, ,
, .
又为的中点, ,
,
, .
,, ,
,
,
,即为 的中点.
图(2)
命题点2 平行四边形的判定[8年3考]
4.[2021福州质检] 下列四个命题:
①一组对边平行,一组对角相等的四边形是平行四边形;
②一组对边平行,另一组对边相等的四边形是平行四边形;
③一组对边相等,一组对角相等的四边形是平行四边形;
④一组对边相等,另一组对边也相等的四边形是平行四边形.
其中假命题是______.(只填序号)
②③
5.[2019福建中考,21] 在中, , .将
绕点顺时针旋转一个角度 得到,点,的对应点分别为, .
(1)若点恰好落在边上,如图(1),连接,求 的大小;
图(1)
[答案] 在中, , ,
.
由旋转的性质得,, ,
.
又 ,
.
(2)若 ,为的中点,如图(2),连接,, ,求证:四边
形 是平行四边形.
图(2)
证明:在中, , ,
.
是 的中点,
,
,
.
由旋转的性质得,, , ,
.
如图,延长交于点,则 ,
, ,
四边形 是平行四边形.
命题点3 多边形的相关计算[8年7考]
6.[2023三明质检] 正八边形的中心角度数为( )
B
A. B. C. D.
(第7题)
7.[2024厦门质检] 如图,是正六边形 的中
心.在平面直角坐标系中,若点的坐标为,点 的坐
标为,则点 的坐标为( )
C
A. B. C. D.
(第8题)
8.[2021福建中考,7] 如图,点在正五边形 的内部,
为等边三角形,则 等于( )
C
A. B. C. D.
9.[2024泉州质检] 正九边形的外角和等于_____ .
360
(第10题)
10.[2023福州质检] 两个正方形按如图所示的位置放置,若重叠
部分是一个正八边形,则这两个正方形边长的比值是___.
1
第五章 四边形
第一部分 中考考点梳理
第一节 平行四边形与多边形
2025年中考数学一轮复习
考点梳理
1.平行四边形的性质与判定[重点]
(1)定义:两组对边①__________的四边形叫做平行四边形.
(2)性质与判定
分别平行
图形 元素 性质 判定 文字语言 符号表示
__________________________________ 边 两组对边 分别平行. 两组对边分别② ______的四边形 是平行四边形. (定义法) 四边形
是平行四边形.
平行
图形 元素 性质 判定 文字语言 符号表示
__________________________________ 边 两组对边 分别相等. 两组对边分别相 等的四边形是平 行四边形. 四边形
是平行四边形.
有一组对边 ③____________ 的四边形是平行 四边形. 或
四边形
是平行四边形.
平行且相等
图形 元素 性质 判定 文字语言 符号表示
__________________________________ 角 两组对角 分别相等. 两组对角分别④ ______ 的四边 形是平行四边形. 四边
形 是平行四边形.
邻角互补. 对角线 对角线互 相平分. 对角线互相 ⑤______的四边 形是平行四边形. 四边形
是平行四边形.
相等
平分
(3)平行四边形的对称性:平行四边形是中心对称图形,两条对角线的交点
是它的对称中心.
(4)平行四边形(如上表格中的图)的面积: ⑥____
.
【易失分点】 与平行四边形的证明和计算有关的常见误区
①注意平行四边形的面积公式不要与三角形的面积公式相混淆.
②一组对边平行,另一组对边相等的四边形不一定是平行四边形,可能是等腰梯形.
③平行四边形不是轴对称图形.
【提分指南】①平行四边形两个邻角的平分线互相垂直,两个对角的平分线
互相平行(或共线).
②平行四边形被任意一条对角线分成面积相等的两个三角形,被两条对角线
分成面积相等的四个三角形;过平行四边形对角线交点的任意一条直线平分
平行四边形的面积.
③当平行四边形中有角平分线的条件时,可利用“平行角平分线 等腰三
角形”的结论得到等角等边,如图(1).
图(1)
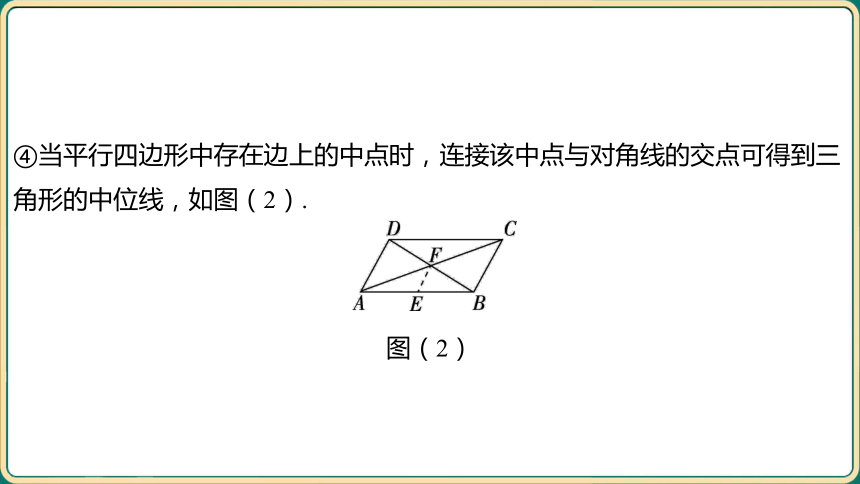
④当平行四边形中存在边上的中点时,连接该中点与对角线的交点可得到三
角形的中位线,如图(2).
图(2)
回练课本
图(1)
1.(1)如图(1),在四边形中, .添加下列
条件后,仍不能判定该四边形 为平行四边形的是( )
D
A. B. C. D.
图(2)
(2)如图(2),两张对边平行的纸条,随意交叉叠放在一起,
重合的阴影部分构成了一个四边形,转动其中一张纸条,则下
列结论一定成立的是( )
B
A. B.
C. D.
(3)在平面直角坐标系中,若以,, 三点为顶点画
平行四边形,则第四个顶点不可能在( )
C
A.第一象限 B.第二象限 C.第三象限 D.第四象限
图(3)
(4)如图(3),四边形 是平行四边形,
,平分且交于点,且交 于
点,则 的大小为_____.
图(4)
(5)已知四边形是平行四边形,如图(4),若 平
分, ,则 的度数为______.
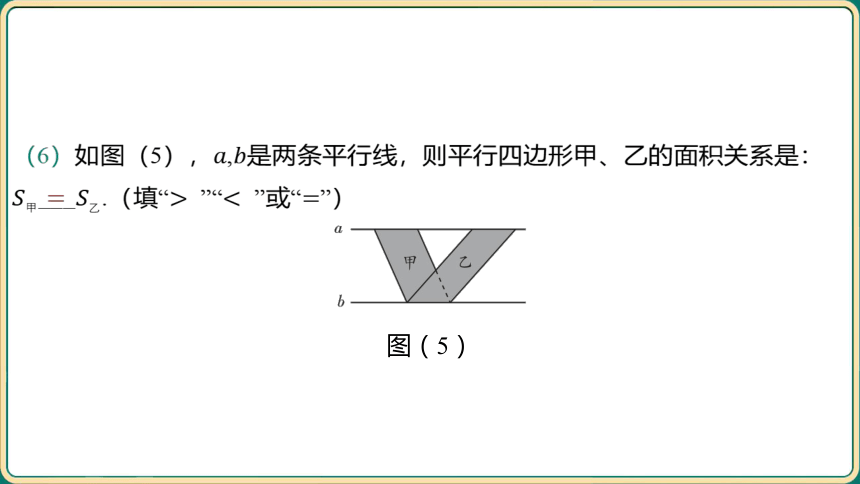
(6)如图(5),, 是两条平行线,则平行四边形甲、乙的面积关系是:
___.(填“ ”“ ”或“ ”)
图(5)
2.多边形[重点]
(1)与多边形有关的计算
边形 ( , 且 为整 数) 内角和定理 边形的内角和为 .
外角和定理 边形的外角和为⑦______.
对角线 过边形的一个顶点可引出 条对
角线;边形共有 条对角线.
(2)正多边形及其性质
正 边形 ( , 且 为整 数) 边、角 正多边形的各边相等,各角相等.
内角、 外角 每一个内角的度数为 ,每一个外角的度数为
.
正 边形 ( , 且 为整 数) 对称性 (1)正边形有 条对称轴;
(2)当为奇数时,正 边形是轴对称图形,但不是
中心对称图形;当为偶数时,正 边形既是轴对称图
形,又是中心对称图形.
(3)正 边形有一个外接圆和一个内切圆,它们是同心
圆.
【注意】 每条边都相等的多边形不一定是正多边形,因为它的内角不一定都
相等,如菱形;每个内角都相等的多边形也不一定是正多边形,因为它的边不一
定相等,如矩形.
2.(1)若正多边形的一个外角的度数为 ,则这个正多边形的边数为___.
(2)正多边形一个内角的度数是 ,则该正多边形的边数是____.
(3)如图,在正六边形中,连接,相交于点,则
______.
8
12
回练课本
考法1 平行四边形的性质与判定
例1 如图,在中,点,,分别为 ,
,边上的点,与相交于点 .
(1)当 时,添加一个条件:______________________
__________,使得四边形 为平行四边形.
答案不唯一,如或
(2)当 时,添加一个条件:_______________________________
________________,使得四边形 为平行四边形.
(3)当 时,添加一个条件:_________________________________
______________________,使得四边形 为平行四边形.
答案不唯一,如,或
答案不唯一,如,或
解题通法
平行四边形的判定思路
证这组对边平行;
证另一组对边相等.
证这组对边相等;
证另一组对边平行.
证另一组对角相等;
证一组对边平行.
4.已知一条对角线平分另一条对角线,证对角线互相平分.
1.已知一组对边相等
2.已知一组对边平行
3.已知一组对角相等
例2 已知四边形 是平行四边形.
图(1)
(1)如图(1),若点是边的中点,点 为对角线的交
点,的周长为6,则 的周长为____.
12
图(2)
(2)如图(2),于点,若 ,
,,则 的周长为__________.
(3)如图(3),,相交于点,,, .
图(3)
①的面积为_____, 的面积为_ ___;
②的长为_ __, 的长为_____;
③若点是的中点,连接交于点,则 的长为_ ___.
解法提示:,, ,
.又, .
解题通法
利用平行四边形的性质进行相关计算的方法
1.求角度:先将题中的已知角找出来,再结合平行四边形的性质(即对角相等,
邻角互补及对边平行),将所求角与已知角联系起来.
2.求线段长:
(1)根据平行四边形的性质将已知条件转化到一个三角形中,利用勾股定
理、直角三角形的性质、等腰三角形的性质、三角函数或三角形面积公式等
进行求解;
(2)根据平行四边形的性质,利用中位线定理、平行线分线段成比例、全
等三角形的判定与性质或相似三角形的判定与性质等进行求解.
考法2 多边形的相关计算
例3 已知一个 边形.
(1)若 ,则它的内角和为______,外角和为______.
(2)若它的每一个内角都为 ,则___;若它的每一个外角都为 ,
则 ___.
(3)如图(1),在正五边形中, 的度数为_____.
8
9
图(1)
(4)①如图(2),在正六边形中,若,则 的长为____;
图(2)
图(3)
②如图(3),点为正六边形对角线 上一点,
,,则 的值是____.
30
[解析] 解法提示:如图(1),连接,易知四边形
为矩形,, ,
, .如图(2),正六边形
被分割成6个面积相等的三角形,可知每个三角形的面积均为
, .
图(1)
图(2)
命题点1 平行四边形的性质[8年3考]
1.[2024宁德质检] 如图,在中, ,则 的度数是( )
B
(第1题)
A. B. C. D.
(第2题)
2.[2023福建中考,12] 如图,在中, 为
的中点,过点且分别交,于点, .若
,则 的长为____.
10
3.[2022三明质检] 已知:如图,在中,为的中点, 于
点,于点 .
求证:
(1) ;
证明: 四边形 为平行四边形,
, .
, ,
,
,
,
.
(2)为 的中点.
[答案] 证法一:如图(1),延长交于点 ,
图(1)
四边形 为平行四边形,
, .
, ,
,
,
四边形 为平行四边形,
图(1)
.
为的中点, ,
.
, ,
,即为 的中点.
图(1)
证法二:如图(2),延长,交于点 .
图(2)
四边形 为平行四边形,
, ,
, .
又为的中点, ,
,
, .
,, ,
,
,
,即为 的中点.
图(2)
命题点2 平行四边形的判定[8年3考]
4.[2021福州质检] 下列四个命题:
①一组对边平行,一组对角相等的四边形是平行四边形;
②一组对边平行,另一组对边相等的四边形是平行四边形;
③一组对边相等,一组对角相等的四边形是平行四边形;
④一组对边相等,另一组对边也相等的四边形是平行四边形.
其中假命题是______.(只填序号)
②③
5.[2019福建中考,21] 在中, , .将
绕点顺时针旋转一个角度 得到,点,的对应点分别为, .
(1)若点恰好落在边上,如图(1),连接,求 的大小;
图(1)
[答案] 在中, , ,
.
由旋转的性质得,, ,
.
又 ,
.
(2)若 ,为的中点,如图(2),连接,, ,求证:四边
形 是平行四边形.
图(2)
证明:在中, , ,
.
是 的中点,
,
,
.
由旋转的性质得,, , ,
.
如图,延长交于点,则 ,
, ,
四边形 是平行四边形.
命题点3 多边形的相关计算[8年7考]
6.[2023三明质检] 正八边形的中心角度数为( )
B
A. B. C. D.
(第7题)
7.[2024厦门质检] 如图,是正六边形 的中
心.在平面直角坐标系中,若点的坐标为,点 的坐
标为,则点 的坐标为( )
C
A. B. C. D.
(第8题)
8.[2021福建中考,7] 如图,点在正五边形 的内部,
为等边三角形,则 等于( )
C
A. B. C. D.
9.[2024泉州质检] 正九边形的外角和等于_____ .
360
(第10题)
10.[2023福州质检] 两个正方形按如图所示的位置放置,若重叠
部分是一个正八边形,则这两个正方形边长的比值是___.
1
同课章节目录
