2025年中考数学一轮复习 -第五章 四边形-第二节 矩形、菱形、正方形 课件(共74张PPT)

(共74张PPT)
第五章 四边形
第一部分 中考考点梳理
第二节 矩形、菱形、正方形
2025年中考数学一轮复习
考点梳理
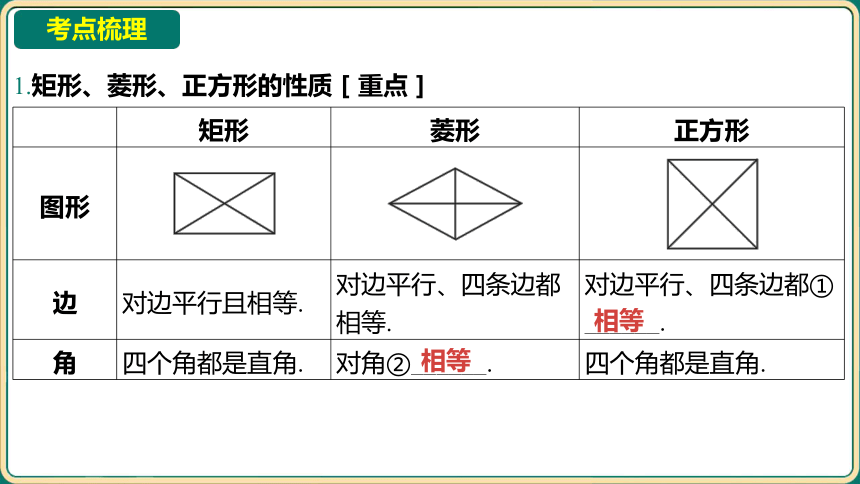
1.矩形、菱形、正方形的性质［重点］
矩形 菱形 正方形
图形 _____________________________ ______________________________________ __________________________
边 对边平行且相等. 对边平行、四条边都 相等. 对边平行、四条边都①
______.
角 四个角都是直角. 对角②______. 四个角都是直角.
相等
相等
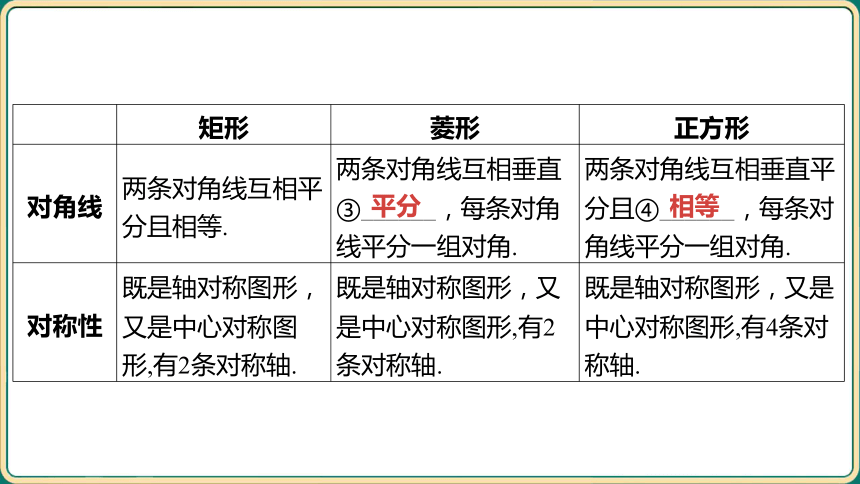
矩形 菱形 正方形
对角线 两条对角线互相平 分且相等. 两条对角线互相垂直 ③______，每条对角 线平分一组对角. 两条对角线互相垂直平
分且④______，每条对
角线平分一组对角.
对称性 既是轴对称图形， 又是中心对称图 形,有2条对称轴. 既是轴对称图形，又 是中心对称图形,有2 条对称轴. 既是轴对称图形，又是
中心对称图形,有4条对
称轴.
平分
相等
矩形 菱形 正方形
面积 ⑤____ （， 分别表示 矩形的长和宽） ⑥______ （, 分别表示两条 对角线的长） （表示一边长, 表示 这条边上的高） ⑦____
（表示边长）
⑧____（ 表示对角线
的长）
回练课本
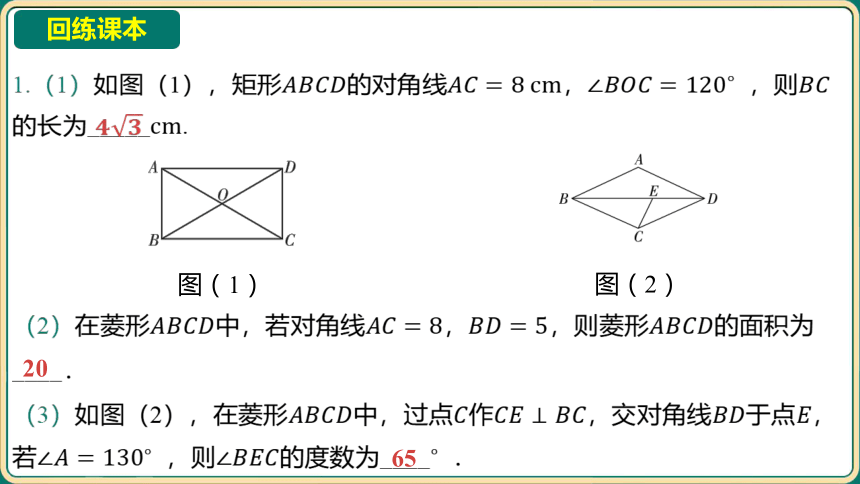
1.（1）如图（1），矩形的对角线， ，则
的长为_____ .
图（1）
图（2）
（2）在菱形中，若对角线，，则菱形 的面积为
____．
（3）如图（2），在菱形中，过点作，交对角线于点 ，
若 ，则的度数为____ ．
20
65
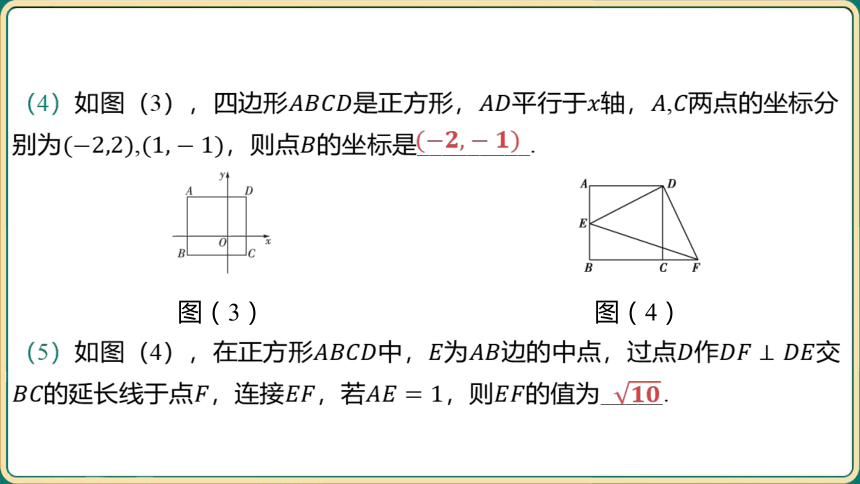
（4）如图（3），四边形是正方形，平行于轴，, 两点的坐标分
别为,，则点 的坐标是_________.
图（3）
图（4）
（5）如图（4），在正方形中，为边的中点，过点作 交
的延长线于点，连接，若，则 的值为_____.
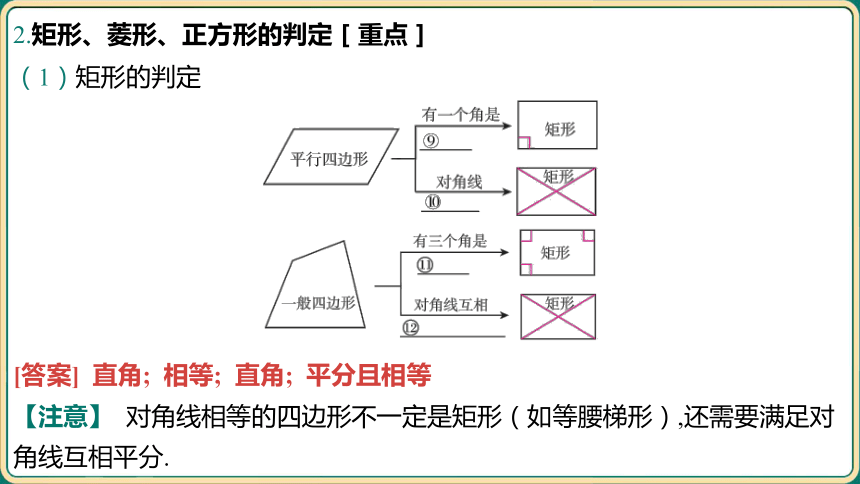
2.矩形、菱形、正方形的判定［重点］
（1）矩形的判定
[答案] 直角; 相等; 直角; 平分且相等
【注意】 对角线相等的四边形不一定是矩形（如等腰梯形）,还需要满足对
角线互相平分.
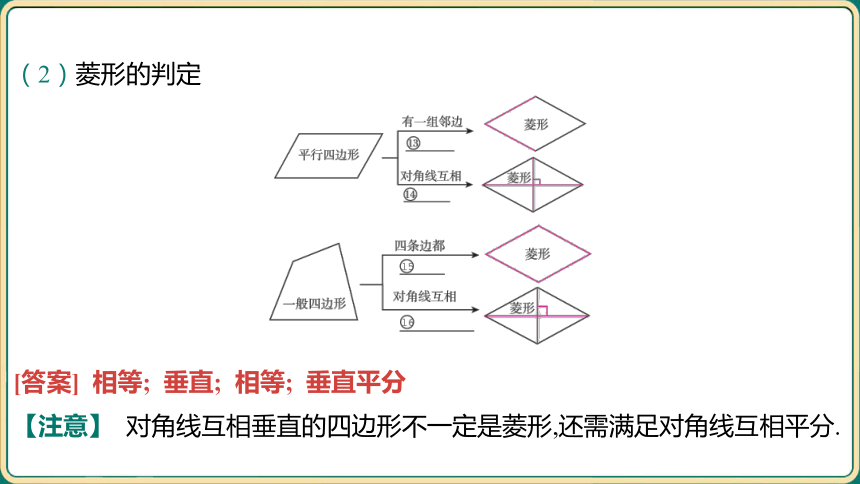
（2）菱形的判定
[答案] 相等; 垂直; 相等; 垂直平分
【注意】 对角线互相垂直的四边形不一定是菱形,还需满足对角线互相平分.
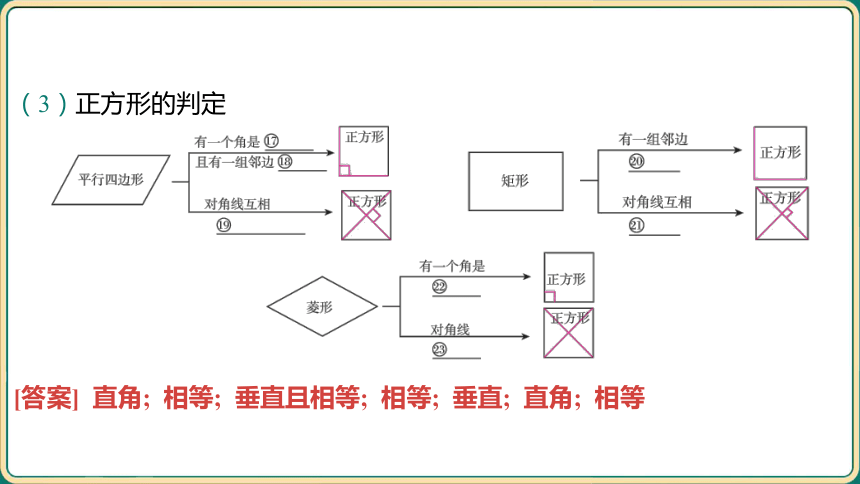
（3）正方形的判定
[答案] 直角; 相等; 垂直且相等; 相等; 垂直; 直角; 相等
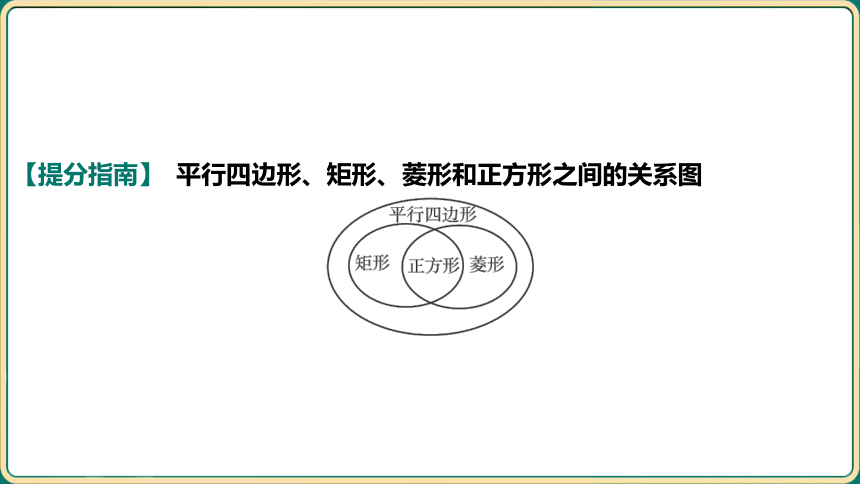
【提分指南】 平行四边形、矩形、菱形和正方形之间的关系图
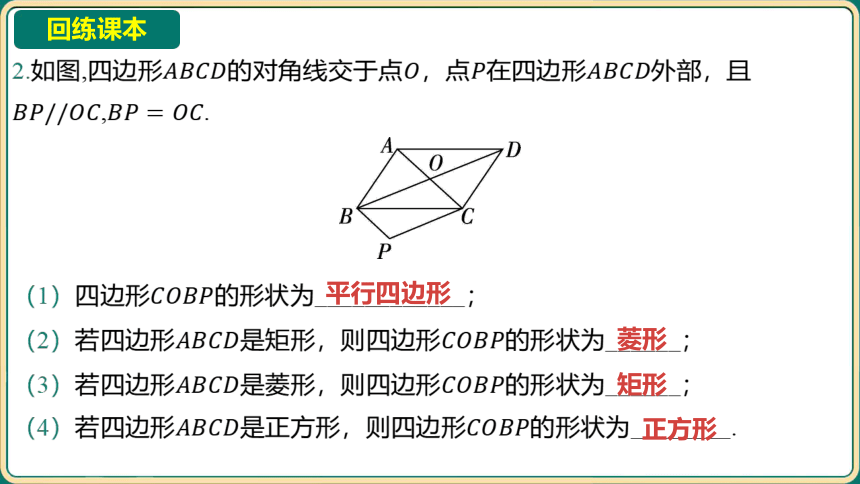
2.如图,四边形的对角线交于点，点在四边形 外部，且
, .
（1）四边形 的形状为____________；
（2）若四边形是矩形，则四边形 的形状为______；
（3）若四边形是菱形，则四边形 的形状为______；
（4）若四边形是正方形，则四边形 的形状为________.
平行四边形
菱形
矩形
正方形
回练课本
课时一 矩形
考法1 矩形的判定与性质
例1（1） 已知四边形 为平行四边形．
①要使四边形 为矩形，则还需添加一个条件：_____________________
____ ．
答案不唯一，如
②如图（1），的对角线,交于点，点为 上一点，连接
并延长，交于点，连接， .
图（1）
（i）若，，，，求证：四边形 为矩
形．
（ii）若，求证:四边形 为矩形．
证明： 四边形 为平行四边形，
， ，
.
又 ，
，
，
四边形 为平行四边形.
，， ，
.
又 ，
，
，
平行四边形 为矩形.
,
,
,
,
平行四边形 为矩形.
（2）在矩形中，， .
①如图（2），将矩形绕其顶点顺时针旋转 ，
得到矩形 ，若点恰好落在的延长线上，
则 的度数为______．
[解析] 解法提示：连接，， ,， ，
， ， .由旋转可知 .
又 点恰好落在的延长线上，，平分 ，
.
图（2）
②如图（3），将矩形绕其顶点逆时针旋转，得到矩形 ，若
点恰好落在对角线上，连接交于点，则 的长为_ ___．
图（3）
[解析] 解法提示：易知 .由旋转得 ，
，为等边三角形， ，
.由旋转易得 ， ，
，， .
（3）在矩形中，，，是的中点，是 边上的
一个动点．将沿所在的直线折叠，点的对应点为 ．
①如图（4）,当点与点重合时， 的值为 .
图（4）
图（1）
[解析] 解法提示：是的中点，， .如图
（1），过点作于点，延长交于点 ，则
四边形是矩形.由折叠得 ，
， ，
, 易证
，.设 ，则
， ,
,
（不合题意的值已舍），, ,
.
②如图（5），连接，则 的最小值为___ .
2
图（2）
[解析] 解法提示：由折叠可知， 点 在以
点为圆心， 为半径的一段圆弧上，如图（2）.∵A1C≥
CE-A1E， 当点在上时， 最小，最小值为
的长.易知, 的最小值为
.
解法指导
（3）①要求的值，联想到过点作的垂线.由折叠得对应
角、对应边分别相等，由直角联想到构造“一线三直角”模型，
再利用相似三角形的性质、矩形的性质、直角三角形的性质即可求解.
②要求的最小值，需找出动点的运动轨迹.由题可知点的运动轨迹是
一段圆弧，进而可将求的最小值，转化为求点到圆弧上一点的距离的
最小值，再利用“点圆最值”模型即可求解.
课时二 菱形
考法2 菱形的判定与性质
例2 如图（1），在四边形中，， ，对角
线，相交于点，平分 ．
图（1）
（1）用三种方法证明四边形 为菱形．
[答案] 证法一：平分 ， .
，
， ，
.
解题指导
（1）证法一：利用一组邻边相等的平行四边形是菱形进行证明．
证法二：利用对角线互相垂直平分的四边形是菱形进行证明.
证法三：利用四条边都相等的四边形是菱形进行证明．
，
,
四边形 为平行四边形.
又 ，
平行四边形 为菱形.
证法二：，平分 ，
，垂直平分 .
，
，
，
.
又 ，
，
， 互相垂直平分，
四边形 为菱形.
证法三：，平分 ，
，垂直平分 ，
.
，
，
，
，
，
四边形 为菱形.
（2）若，，则四边形的面积为____， __．
16
（3）如图（2），,垂足为，连接，若 ，则
的度数为_____．
图（2）
图（3）
图（4）
图（5）
（4）如图（3），为边的中点，为边上一点，连接， ，若
，，则 的长为___．
6
图（1）
解法提示：如图（1），延长交 的延长线于
点 四边形为菱形， ，
，为 的中点，
，， ，
，,，，即 .又
，，，即， .
. .
. .
（5）如图（4），若， ，，分别是， 的中点，
，分别是，的中点，连接，则 的长为___．
1
图（2）
解法提示：如图（2），连接并延长交 于点
，连接， 四边形 为菱形，
，,， 是等边三角
形，， ，
为中点，， ，
，是的中点, 点,分别是, 的中点.又
，分别为，的中点， .
. .
. .
（6）如图（5），若， ，，分别是， 边上的点，
且，连接，将沿折叠，得到，连接 ,
则 的长为_____．
图（3）
[解析] 解法提示：过点作于点，如图（3）.
四边形是菱形, ,, ,
.由折叠得, 四边形
是菱形, .在 中,
, ,
, , 在
中， .
. .
. .
解题指导
（3）方法一：利用菱形的性质和是的中线求解.
方法二：借助隐形圆（,，，四点共圆），利用圆周角定理的推论求解.
（4）由联想到构造全等三角形，再结合得到相似三角形，进而求解．
（5）由联想到构造中位线模型进行求解．
（6）由可判定四边形的形状.要求的长，可联想到构造直角
三角形，再利用勾股定理进行求解.
解题通法
利用菱形的性质进行相关计算的一般思路
1.求角度时，应注意菱形的四条边相等、对角相等、邻角互补等，可利用等腰
三角形的性质和平行线的相关性质转化要求的角，直到找到与已知角的关系.
2.求长度（线段或周长）时，应注意利用等腰三角形的性质;若菱形的一个内
角为 ，则短对角线所分割的两个三角形为等边三角形，在计算时可利用
等边三角形的性质;若菱形中存在直角三角形，则可利用勾股定理、直角三角
形斜边上的中线等于斜边的一半、含特殊角的直角三角形的性质等进行计算.
3.求面积时，有底×高和 两条对角线长的积两种方法，可
根据所给的条件选择合适的方法．
提分特训
1.[2024山西中考改编] 如图（1）,四边形是菱形,过点作 于
点,过点作于点 .
图（1）
图（2）
（1）判断四边形 的形状,并说明理由.
[答案] 四边形 为矩形.
理由如下：
四边形 为菱形
，
四边形 为矩形.
（2）将图（1）中的绕点逆时针旋转,得到,点, 的对应点分
别为点,.如图（2）,当线段经过点时,所在直线分别与线段,
交于点,.猜想线段与 的数量关系,并说明理由.
[答案] .
理由如下:
方法一:
四边形 为菱形，
.
旋转得到 ，
图（2）
，
.
又 ，
，
,
图（2）
方法二：如图，连接
四边形 为菱形，
，，
旋转得到 ，
，
又
.
课时三 正方形
考法3 正方形的判定与性质
例3 如图（1），在矩形中，，分别是， 边上的点，若
，垂足为，且 ．
图（1）
（1）求证：矩形 是正方形．
证明： 四边形 是矩形，
.
，
，
.
又 ，
，
，
矩形 为正方形.
图（1）
图（2）
（2）如图（2），四边形的对角线, 相交于点
，交于点，若平分 ．
①求证：平分 .
证明：由（1）可知，四边形 是正方
形，
, .
平分 ，
，
，
平分 .
②连接，求证： ．
证明：由（1）可知四边形 是正方形，
.
，平分 ，
, .
又, ,
，
.
图（2）
例4 如图（1），已知正方形，为对角线上一点．是 延长线上
一点，，交于点 ．
图（1）
（1）求证： .
证明： 四边形 为正方形，
， .
又 ，
，
.
四边形为正方形， ，
， ，
，
.
图（1）
图（2）
（2）如图（2），若为的中点，且，连接 ，
则 的长为_____．
[解析] 解法提示：过点作，垂足为 四边形
为正方形，为的中点，， ，
，， ，
，， .
（3）若,求证： ．
证明：设，则易知 .
，
.
由（1）可知 ，
，
.
提分特训
2.[2024扬州中考节选] 如图,点,,,, 依次在直
线上,点，固定不动,且, ,分别以
，为边在直线同侧作正方形 、正方形
， ,直角边恒过点 ,直角边
恒过点 .
（1）若,求点与点 之间的距离;
[答案] 设，则 .
在正方形中， ，， .
在正方形中， ， ,
， .
， ，
.
又 ，
，
，即，则 ，
解得， ，
故点与点 之间的距离为4或6.
（2）当点在点，之间运动时,求 的最大值.
[答案] 设，则 .
在正方形中， ，， .
在正方形中， ，
， .
， ，
.
又 ，
，
，即 ，
.
故当时，取最大值，最大值为 .
命题点1 与矩形有关的证明与计算［8年7考］
（第1题）
1.[2023厦门质检] 小梧要在一块矩形场地上晾晒用传统
工艺制作的蜡染布.如图所示,该矩形场地北侧安有间隔相
等的7根栅栏,其中4根栅栏处与南侧的两角分别固定了高
度相同的木杆,,,, .这些木杆顶部的相同位置都钻有
C
A. B. C. D.
孔,绳子穿过木杆上的孔可以被固定.小梧想用绳子在南侧的两条木杆, 和北
侧的一条木杆上连出一个三角形,以晾晒蜡染布.小梧担心手中绳子的总长度
不够,那么他在北侧木杆中应优先选择( )
（第2题）
2.[2023厦门质检] 如图,在矩形中,对角线, 交于
点,, ,则 的长为___.
2
（第3题）
3.[2024漳州质检] 如图,四边形的对角线, 相交于
点,,过点作交于点 ,若
,,则 的长为_____.
4.[2021福建中考，16] 如图，在矩形中， ，
，点，分别是边,上的动点，点不与， 重
合，且，是五边形内满足 且
的点.现给出以下结论：
与 一定互补；
②点到边， 的距离一定相等；
③点到边， 的距离可能相等；
④点到边的距离的最大值为 .
其中正确的是________.（写出所有正确结论的序号）
①②④
命题点2 与菱形有关的证明与计算［8年5考］
（第5题）
5.[2022厦门质检] 如图，菱形的对角线， 交于
点，点是边的中点，点在边上，且 ．将
点平移到点 ，则平移的距离等于( )
C
A. B. C. D.
（第6题）
6.[2023福建中考，13] 如图，在菱形中， ，
，则 的长为____.
10
（第7题）
7.[2023泉州质检] 如图,在菱形中, ,点
在边上,以为边在菱形 的内部作等边三角形
,若 , ,则 与 之间的数量关
系可用等式表示为____________.
8.[2024龙岩质检] 在边长为6的菱形中，点,分别是, 上的点，
且，是直线上的动点，则 的最大值为___．
4
命题点3 与正方形有关的证明与计算［8年5考］
（第9题）
9.[2024南平质检] 如图，已知正方形的边长为6, ,
分别是,边上的点,且 ,将绕点
逆时针旋转 ,得到.若,则 的长为
( )
B
A.4 B.5 C.6 D.6.5
（第10题）
10.[2024福建中考，14] 如图，正方形的面积为4,点, ,
,分别为边,,,的中点，则四边形 的面积为___.
2
（第11题）
11.[2024泉州质检] 如图，在正方形中，对角线 与
相交于点，以点为圆心，以的长为半径作弧，交
于点，连接，则_____ ．
22.5
12.[2024南平质检] 已知矩形纸片 .
第1步:先将矩形纸片对折,使点和点重合,然后展开铺平,确定 的中
点 ；
第2步:将边沿折叠到的位置,点的对应点为 ;
第3步:连接并延长,交于点 .
（1）当四边形 为正方形,如图（1）.
图（1）
①用尺规作出点, （不写作法,保留作图痕迹）;
[答案] 作图如图（1）或图（2）所示，点， 即为所求作的点.（作法不唯
一，正确作出一种即可）
图（1）
图（2）
②求证： .
图（3）
证明：如图（3），连接 .
四边形 是正方形，
, .
由折叠可得 ，
, ,， ,
.
又 ，
，
.
设， .
为的中点， ，
， .
在中，根据勾股定理,得，解得 ，
， ，
.
图（3）
（2）如图（2）,延长,交于点,连接,,当恰为的中点时,求
的值.
图（2）
[答案] 四边形 是矩形，
,, .
由折叠可得 ，
,, ，
, .
为的中点,为 的中点，
, ，
，
图（2）
， .
设，，则, ,
,
, .
在中，由勾股定理，得，
解得 ，
.
图（2）
新课标 新考向
【新考向·新定义】[2024盐城中考] 如图（1）,,,,分别是 各边
的中点,连接,交于点,连接，交于点,将四边形 称为
的“中顶点四边形”.
图（1）
（1）求证:中顶点四边形 为平行四边形.
证明: 四边形 为平行四边形,
,,, .
点,,,分别是 各边的中点,
, ,
四边形 为平行四边形.
同理可得，四边形 为平行四边形,
, ,
四边形 是平行四边形.
图（1）
（2）①如图（2）,连接,交于点,可得，两点都在上,当
满足________________________时,中顶点四边形 是菱形;
（答案不唯一）
图（2）
②如图（3）,已知矩形 为某平行四边形的中顶点四边形,请用无刻度的
直尺和圆规作出该平行四边形.（保留作图痕迹,不写作法）
图（3）
[答案] 如图, 即为所求.
（答案不唯一）
[解析] 解法提示：连接,作直线交于点，作 ,
,顺次连接即可得到所求作的平行四边形.