2025年中考数学一轮复习 -第六章 圆-第一节 与圆有关的概念及性质 课件(共41张PPT)

(共41张PPT)
第六章 圆
第一部分 中考考点梳理
第一节 与圆有关的概念及性质
2025年中考数学一轮复习
考点梳理
1.与圆有关的概念［基础点］
圆 在同一平面内，一条线段绕着它固定的一个端点旋 转一周，另一个端点所形成的图形叫做圆. ___________________________________
圆是平面内到定点的距离等于定长的所有点组成的 图形. 圆心角 顶点在①______的角叫做圆心角，如 . 圆心
圆周角 顶点在圆上，并且两边都与圆相交的角叫做圆周 角，如 . ___________________________________
弦 连接圆上任意两点的线段叫做弦，如弦 .经过圆 心的弦叫做②______，如 . 圆弧 圆上任意两点间的部分叫做圆弧，简称弧.大于半圆 的弧叫做③______，如 ；小于半圆的弧叫做 ④______，如 . 等弧 在同圆或等圆中，能够互相重合的弧叫做等弧. 直径
优弧
劣弧
【提分指南】 .不在同一直线上的三点可以确定一个圆.
.圆的对称性:圆既是轴对称图形,又是中心对称图形,任意一条直径所在的直
线都是它的对称轴,圆心是它的对称中心.
.圆的旋转不变性:将圆绕它的圆心任意旋转一个角度,都能与原来的圆重合.
回练课本
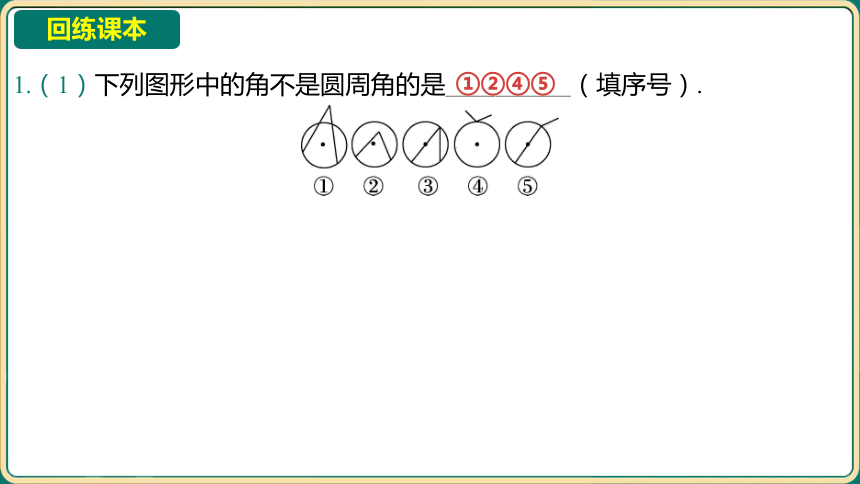
1.（1）下列图形中的角不是圆周角的是__________（填序号）.
①②④⑤
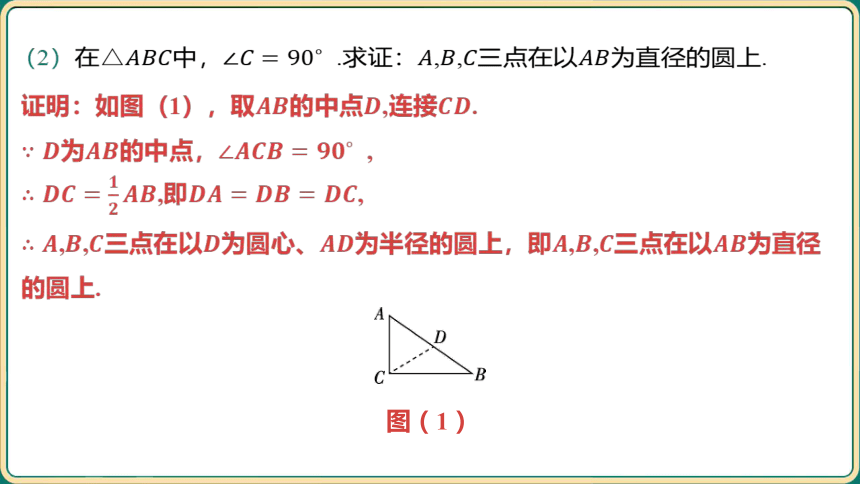
（2）在中， .求证：,,三点在以 为直径的圆上.
证明：如图（1），取的中点,连接 .
为的中点， ,
,即 ,
,,三点在以为圆心、为半径的圆上，即,,三点在以 为直径
的圆上.
图（1）
（3）求证：直径是圆中最长的弦.
证明：如图（2），点,在以为直径的上，且,, 三点不共线，
则 .
,,是的三边， ,
，即直径是圆中最长的弦.
图（2）
2.弦、弧、圆心角之间的关系［重点］
（1）定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
（2）推论:
.在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角⑤______,所对的
弦⑥______.
.在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角⑦______,所对的
优弧和劣弧分别⑧______.
相等
相等
相等
相等
【提分指南】 在同圆或等圆中,两个圆心角、两条弧、两条弦、两条弦的弦
心距,如果其中有一组量相等,那么它们所对应的其余各组量也分别相等.
2.如图，四边形内接于， .有如下结论：
;平分;的垂直平分线经过点 ;④
连接，，，若，则 ;⑤若
，的半径为5，则 .则正确的结论为
________.（填序号）
①②③
回练课本
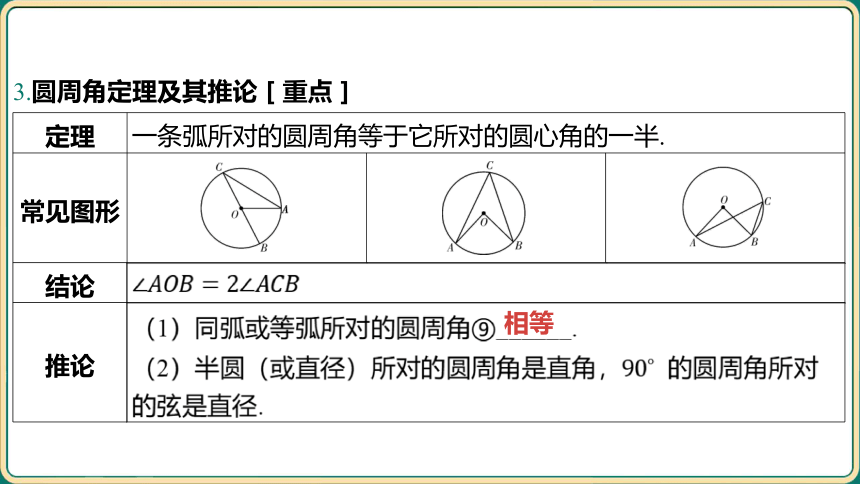
3.圆周角定理及其推论［重点］
定理 一条弧所对的圆周角等于它所对的圆心角的一半. 常见图形 __________________________ ________________________ _________________________
结论 推论 （1）同弧或等弧所对的圆周角⑨______. （2）半圆（或直径）所对的圆周角是直角， 的圆周角所对 的弦是直径. 相等
图（1）
3.（1）如图（1）,是的内接三角形, ,连接
，,则_____ .
图（2）
（2）如图（2），是的直径，，是 的两条弦，
且，则 所对的圆周角的度数为_____.
回练课本
50
4.垂径定理及其推论［基础点］
（1）垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧.
（2）推论:平分弦（不是直径）的直径垂直于弦,并且平分弦所对的两条弧.
课标新变化：探索并证明垂径定理由选学内容调整为考查内容.
【拓展】 .平分弦所对的一条弧的直径垂直于弦，并且平分弦所对的另一条
弧；
.弦的垂直平分线经过圆心，并且平分弦所对的两条弧；
.利用垂径定理及其推论解题时，常过圆心向弦作垂线，在计算时，常涉及
半径，弦长，弦心距（圆心到弦的距离），它们之间的关系是
.
【解题通法】 利用垂径定理及其推论解题时常用的辅助线作法
利用垂径定理及其推论解题时,常通过添加辅助线,构造直角三角形,结合勾股
定理或锐角三角函数进行解题.常用辅助线作法:①过圆心作弦的垂线;②连接
圆心和弦的一端（即作半径）;③当条件中有弦的中点（或弦所对弧的中点）
时,连接圆心与弦（或弧）的中点.
4.如图是一款拱门屏风的示意图（以点 为圆心的圆的一部分），
其中拱门屏风最下端分米，为的中点， 为拱门屏
风最高点，圆心在线段上， 分米，则拱门屏风所在
圆的半径是____分米．
15
回练课本
5.圆内接四边形的概念和性质［重点］
概念 四个顶点均在同一个圆上的四边形叫 做圆内接四边形. _______________________________
性质 圆内接四边形对角互补. ⑩______
______
图（1）
5.（1）如图（1），四边形内接于， 为直径，
，连接．若 ，则 的度数为______.
回练课本
（2）如图（2），四边形内接于，若 ，则
_____ ．
140
图（2）
考法1 圆周角定理及其推论
例1 已知：点，，，在 上.
图（1）
（1）若是的直径，点，是 两侧的两点,如图（1），
若 ,则 的度数为_____.
图（2）
（2）如图（2），若直线,交于外点 ，
， ，则 的度数为_____.
（3）如图（3），若是的直径，弦交于点， ，
，，则 的长为_ ___．
图（3）
解法提示：如图，连接,是 的直径，
， .过点 作
于点，如图，则 .
，， ，
，. ,
，，，即 ，
．
考法2 垂径定理及其推论
例2 已知，点，，，是 上的点.
（1）如图（1），， ，则 的度数是_____．
图（1）
（2）若为的直径，弦，垂足为点 .
①如图（2），若，，则 的半径为___．
3
图（2）
图（3）
②如图（3），若点为上一点，且， ，
，则弦 的长为___．
[解析] 解法提示：连接交于点.设的半径为 ，则
,，.在
中，由勾股定理，得，即 ，解得
，.连接，，，垂直平分 ，
， , ，
，即，， .
考法3 圆内接四边形的性质
例3 已知：四边形内接于 .
图（1）
（1）如图（1），,且，连接 .若
,则 的度数为_____.
解法提示：, ，
， ,
， ,
， ,
.
（2）如图（2），是的直径，连接．若 ，则
的度数为_____.
图（2）
解法提示： 四边形是 的内接四边形，
.又，是
的直径， ， .
图（3）
（3）如图（3），若 ， ， ，
，则 的长为________.
解法提示：如图，延长，交于点 四边形
是的内接四边形， ，
， ， ,
， .在中， .在
中，， ．
命题点1 圆周角定理及其推论［8年8考］
（第1题）
1.[2024泉州质检] 如图，等边三角形和正方形 均内
接于，若，则 的长为( )
D
A. B. C. D.
（第2题）
2.[2024福州质检] 如图,是半圆的直径,点
（不与点重合）在上.过点作交半圆 于点
,连接,,.过点作于点.设 ,
,则图中长度一定等于 的线段是____.
3.[2023福州质检] 如图,是半圆的直径,,是
上一点,,是的中点,连接,, .
（1）求 的大小;
[答案] ，
,
是等边三角形，
.
（2）求证: .
证明：如图，连接 .
，
.
，
，即 .
是 的中点，
.
由（1）知 ，
是 的垂直平分线，
，
．
4.[2024福建中考，25] 如图，在中， ,
,以为直径的交于点,,垂足为,
的延长线交于点 .
（1）求 的值；
[答案] ,且是的直径， .
, 在中， .
, 在中， ,
， .
（2）求证： ;
图（1）
证明：如图（1），过点作,交的延长线于点 .
, .
,,, .
， ,
,
, ,
.
, , ,
, ,
.
图（1）
（3）求证：与 互相平分.
图（2）
证明：如图（2），连接, .
是的直径， , .
, ,, .
由（2）知， ,
， ，
, ,
,
,
.
图（2）
由（2）知， ,
.
,
,
,
四边形 是平行四边形，
与 互相平分.
图（2）
命题点2 圆内接四边形的性质［8年2考］
（第5题）
5.[2024漳州质检] 如图,是四边形 的外接圆,连接
,,若 ,则 的大小为( )
D
A. B. C. D.
（第6题）
6.[2023莆田质检] 如图，在中， ，点
在上，连接，，过点作的延长线于点 ，
则点从点运动到点的过程中， 的度数( )
C
A.先增大后减小 B.先减小后增大
C.保持不变 D.一直减小
7.[2023莆田质检] 如图，内接于，的延长线交于点 ，交
于点，过点作交于点，连接， ．
（1）若，求证： ；
证明：由题可知四边形内接于 ，
．
， ，
四边形 为平行四边形，
,
,
，
．
（2）求证：点到的距离等于 的长．
证明：如图，过点作，交于点，连接 ,
则 ．
是 的直径，
,
，
，
，
．
，
，
， 所对的圆心角相等，
，
，即点到的距离等于 的长．