2025年中考数学一轮复习 -第六章 圆-第二节 与圆有关的位置关系 课件(共41张PPT)
文档属性
| 名称 | 2025年中考数学一轮复习 -第六章 圆-第二节 与圆有关的位置关系 课件(共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 13:29:45 | ||
图片预览









文档简介
(共41张PPT)
第六章 圆
第一部分 中考考点梳理
第二节 与圆有关的位置关系
2025年中考数学一轮复习
考点梳理
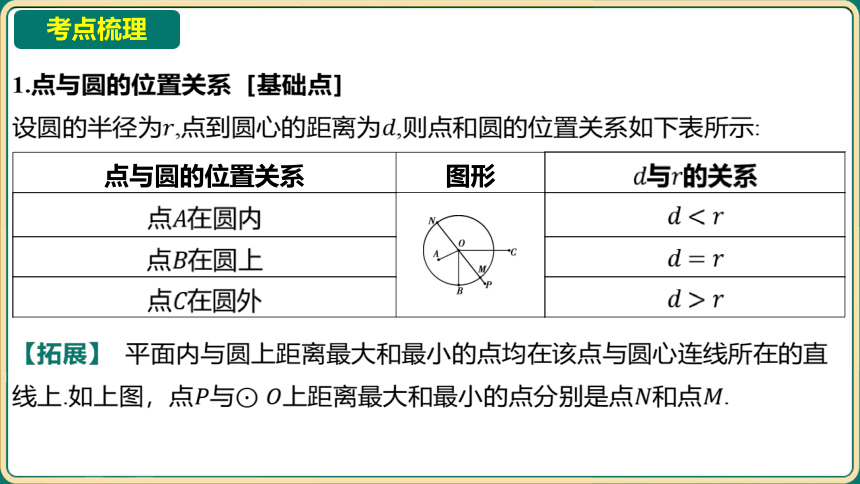
1.点与圆的位置关系[基础点]
设圆的半径为
点与圆的位置关系 图形 与 的关系
点 在圆内 __________________________
点 在圆上
点 在圆外
【拓展】 平面内与圆上距离最大和最小的点均在该点与圆心连线所在的直
线上.如上图,点与上距离最大和最小的点分别是点和点 .
回练课本
1.(1)已知的半径为,点到点的距离是,那么点与
的位置关系是( )
A
A.点在的内部 B.点在 的外部
C.点在 上 D.以上三种都有可能
(2)点是非上一点,若点到上的点的最小距离是 ,最大距
离是,则的半径是_________ .
6.5或2.5
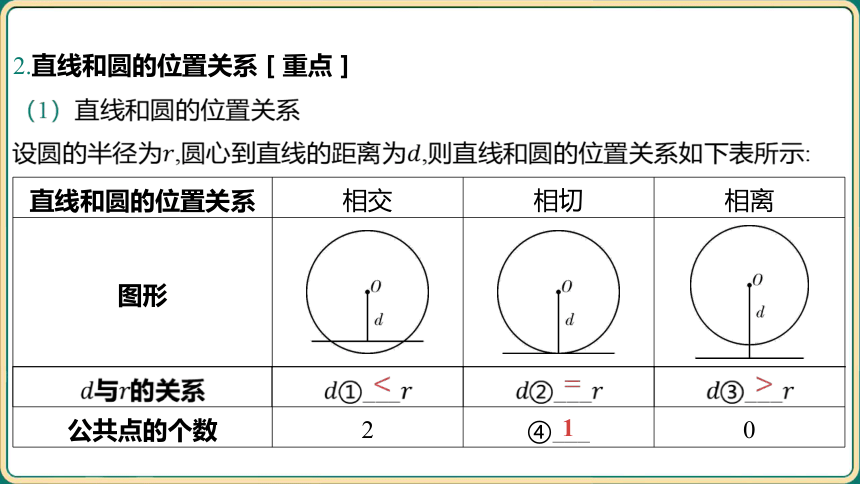
2.直线和圆的位置关系[重点]
(1)直线和圆的位置关系
设圆的半径为,圆心到直线的距离为 ,则直线和圆的位置关系如下表所示:
直线和圆的位置关系 相交 相切 相离
图形 _________________________________ _________________________________ ________________________________
与 的关系 ①___ ②___ ③___
公共点的个数 2 ④___ 0
1
(2)切线
①定义:直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫
做圆的切线,这个点叫做切点.
②性质与判定
性质定理 圆的切线垂直于过切点的半径.
判定 .和圆只有⑤____个公共点的直线是圆的切线.
.如果圆心到一条直线的距离等于圆的⑥______,那么这条直线
是圆的切线.
.经过半径的外端并且垂直于这条半径的直线是圆的切线.
一
半径
③切线长:经过圆外一点的圆的切线上,这点和切点之间线段的长,叫做这
点到圆的切线长.
④切线长定理(选学内容):从圆外一点可以引圆的两条切线,它们的切线长
相等,这一点和圆心的连线平分两条切线的夹角.
2.(1)已知的半径为3,点是直线上的一点,,则直线与
的位置关系是____________.
相切或相交
图(1)
(2)如图(1),是的直径,是的切线,点 在
上.若 ,则 的度数是_____.
回练课本
图(2)
(3)如图(2),,分别与相切于, 两点,
点为上一点,连接,,若 ,则
的度数为_____.
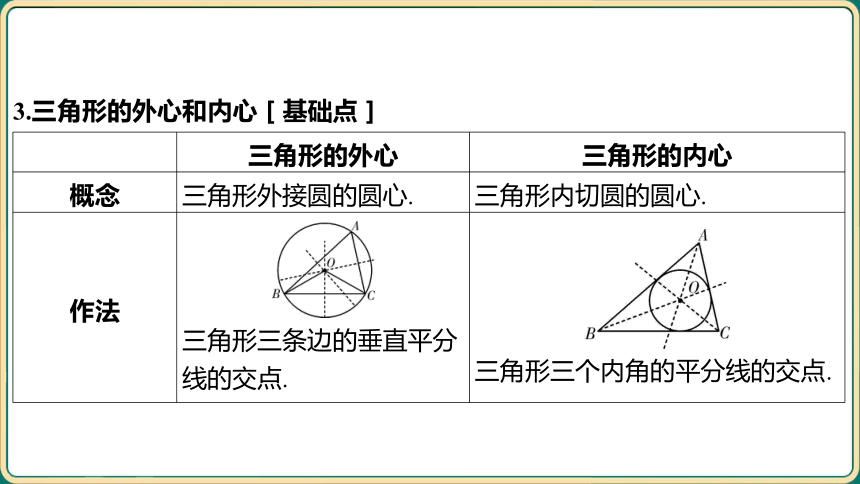
3.三角形的外心和内心[基础点]
三角形的外心 三角形的内心
概念 三角形外接圆的圆心. 三角形内切圆的圆心.
作法 ____________________________ 三角形三条边的垂直平分 线的交点. ______________________________________
三角形三个内角的平分线的交点.
三角形的外心 三角形的内心
性质 三角形的外心到三角形三 个顶点的距离相等. 三角形的内心到三角形三条边的
距离相等.
位置 外心不一定在三角形内. 内心一定在三角形内.
常用角度关系
【特例】 直角三角形的外心为其斜边的中点,其外接圆的半径 ;其内切
圆的半径(其中,为直角边长, 为斜边长).
图(1)
3.(1)如图(1),内接于, ,
,则 的直径长为____.
12
图(2)
(2)如图(2),是的内切圆, ,则
的度数为______.
回练课本
4.正多边形和圆的相关计算[基础点]
设正
边心距 或 ___________________________________
正 边形的周长 正 边形的面积 每个内角的度数 正 边形中心角的度数 正 边形每个外角的度数 【特例】 设正边形的边长为,外接圆半径为.则正六边形: ;正方
形:;正三角形: .
图(1)
4.(1)如图(1),若正方形 的边长为6,则其外接圆半
径与内切圆半径 的比值为____.
图(2)
(2)如图(2),正五边形内接于,点在 上,
则 的度数为_____.
回练课本
考法 切线的性质与判定
例1 [2024陕西中考] 如图,直线与相切于点,是的直径,点, 在
上,且位于点两侧,连接,,分别与交于点,,连接, .
(1)求证: ;
证明: 直线与相切于点 ,
,
.
是 的直径,
,
,
.
(2)若的半径,,,求 的长.
[答案] ,, .
, .
又, ,
, 是等腰直角三角形,
, .
连接 ,
是的直径, ,
.
, ,
.
又 ,
,
,即 ,
.
例2 [2024福州质检] 如图,在中,,为上一点.以为圆心,
长为半径的过点,交于另一点.若是的中点,求证:是 的切线.
证明:如图,连接, .
,
是直径,
.
是 的中点,
.
又 ,
,
,
,
.
又 点为半径的外端点,是 的切线.
例3 [2024自贡中考] 在中, ,是 的内切圆,
切点分别为,, .
图(1)
(1)图(1)中三组相等的线段分别是, ___,
____;若,,则 的半径长为___.
1
图(1)
解法提示:如图(1),连接,,设 的半径
为 ,
是 的内切圆,
,, .
在四边形中, ,
四边形 为矩形.
又 ,
四边形 为正方形,
,, .
在中,由勾股定理得 ,
,即 ,
解得 .
图(1)
(2)如图(2),延长到点,使,过点作 于点
.求证:是 的切线.
图(2)
图(2)
证明:如图(2),过点作于点 ,连接
,, .
,, ,
,
.
,
,即 .
在四边形中, ,
四边形 为矩形.
又 ,
四边形 为正方形,
, .
,
四边形 是矩形,
,
,即是 的半径.
,
是 的切线.
图(2)
解题通法
证明切线常用的两种方法
1.“有公共点,连半径,证垂直”.如果已知圆与直线有公共点,只要证明圆心与公
共点的连线与已知直线垂直即可.
2.“无公共点,作垂线,证半径”.如果已知条件中没有给出直线与圆存在公共点,
应过圆心向这条直线作垂线,然后证明垂线段的长度等于半径即可.
命题点1 切线的性质与判定[8年8考]
(第1题)
1.[2024福建中考,7] 如图,已知点,在 上,
,直线与相切,切点为,且为 的中点,
则 等于( )
A
A. B. C. D.
(第2题图)
2.[2023福州质检] 如图,中,是上一点,以 为圆
心,长为半径作半圆,与相切于点.若 ,
,则 的度数是( )
B
A. B. C. D.
(第3题)
3.[2021福建中考,9] 如图,为的直径,点在
的延长线上,,与相切,切点分别为, .若
,,则 等于( )
D
A. B. C. D.
4.[2024漳州质检] 如图,是的直径,点在上,交于点 ,
为 的切线.
(1)求证: ;
证明:如图,连接 .
是 的切线,
.
是 的直径,
.
,
,
.
又 ,
.
,
,
.
(2)若,,求 的值.
[答案] 由(1)知 , ,
.
, ,
,
.
, ,
,
,
,
.
5.[2023福建中考,21] 如图,已知内接于,的延长线交 于
点,交于点,交的切线于点,且 .
(1)求证: ;
证明:是 的切线,
,即 .
是 的直径,
,
.
,
,
,即 ,
.
(2)求证:平分 .
证明:与都是 所对的圆周角,
.
,
,
.
由(1)知, ,
,
平分 .
6.[2024泉州质检] 如图,是的直径,点在半径上,点在
上,,连接并延长至点,使得,与 的另一个交
点为 .
(1)求证:与 相切;
证明:, .
又, .
, .
是的直径, ,
, ,
,
.
又是的半径,与 相切.
(2)若,,求 的长.
[答案] 与都是 所对的圆周角,
.
在中, .
设,则, ,
,解得 .
经检验, 是原分式方程的解,
, .
在中,由勾股定理,得 ,
.
不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这
种思想得到了圆周率 的近似值为.如图, 的半径为1,运用“割
圆术”,以圆内接正六边形面积近似估
计的面积,可得 的估计值为 ,若用圆内接正十二边形作近似估计,
可得 的估计值为( )
命题点2 正多边形与圆的相关计算[18年1考]
7.[2023福建中考,10] 我国魏晋时期数学家刘徽在“九章算术注”
中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方
法来近似估算,指出“割之弥细,所失弥少,割之又割,以至于
C
A. B. C.3 D.
第六章 圆
第一部分 中考考点梳理
第二节 与圆有关的位置关系
2025年中考数学一轮复习
考点梳理
1.点与圆的位置关系[基础点]
设圆的半径为
点与圆的位置关系 图形 与 的关系
点 在圆内 __________________________
点 在圆上
点 在圆外
【拓展】 平面内与圆上距离最大和最小的点均在该点与圆心连线所在的直
线上.如上图,点与上距离最大和最小的点分别是点和点 .
回练课本
1.(1)已知的半径为,点到点的距离是,那么点与
的位置关系是( )
A
A.点在的内部 B.点在 的外部
C.点在 上 D.以上三种都有可能
(2)点是非上一点,若点到上的点的最小距离是 ,最大距
离是,则的半径是_________ .
6.5或2.5
2.直线和圆的位置关系[重点]
(1)直线和圆的位置关系
设圆的半径为,圆心到直线的距离为 ,则直线和圆的位置关系如下表所示:
直线和圆的位置关系 相交 相切 相离
图形 _________________________________ _________________________________ ________________________________
与 的关系 ①___ ②___ ③___
公共点的个数 2 ④___ 0
1
(2)切线
①定义:直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫
做圆的切线,这个点叫做切点.
②性质与判定
性质定理 圆的切线垂直于过切点的半径.
判定 .和圆只有⑤____个公共点的直线是圆的切线.
.如果圆心到一条直线的距离等于圆的⑥______,那么这条直线
是圆的切线.
.经过半径的外端并且垂直于这条半径的直线是圆的切线.
一
半径
③切线长:经过圆外一点的圆的切线上,这点和切点之间线段的长,叫做这
点到圆的切线长.
④切线长定理(选学内容):从圆外一点可以引圆的两条切线,它们的切线长
相等,这一点和圆心的连线平分两条切线的夹角.
2.(1)已知的半径为3,点是直线上的一点,,则直线与
的位置关系是____________.
相切或相交
图(1)
(2)如图(1),是的直径,是的切线,点 在
上.若 ,则 的度数是_____.
回练课本
图(2)
(3)如图(2),,分别与相切于, 两点,
点为上一点,连接,,若 ,则
的度数为_____.
3.三角形的外心和内心[基础点]
三角形的外心 三角形的内心
概念 三角形外接圆的圆心. 三角形内切圆的圆心.
作法 ____________________________ 三角形三条边的垂直平分 线的交点. ______________________________________
三角形三个内角的平分线的交点.
三角形的外心 三角形的内心
性质 三角形的外心到三角形三 个顶点的距离相等. 三角形的内心到三角形三条边的
距离相等.
位置 外心不一定在三角形内. 内心一定在三角形内.
常用角度关系
【特例】 直角三角形的外心为其斜边的中点,其外接圆的半径 ;其内切
圆的半径(其中,为直角边长, 为斜边长).
图(1)
3.(1)如图(1),内接于, ,
,则 的直径长为____.
12
图(2)
(2)如图(2),是的内切圆, ,则
的度数为______.
回练课本
4.正多边形和圆的相关计算[基础点]
设正
边心距 或 ___________________________________
正 边形的周长 正 边形的面积 每个内角的度数 正 边形中心角的度数 正 边形每个外角的度数 【特例】 设正边形的边长为,外接圆半径为.则正六边形: ;正方
形:;正三角形: .
图(1)
4.(1)如图(1),若正方形 的边长为6,则其外接圆半
径与内切圆半径 的比值为____.
图(2)
(2)如图(2),正五边形内接于,点在 上,
则 的度数为_____.
回练课本
考法 切线的性质与判定
例1 [2024陕西中考] 如图,直线与相切于点,是的直径,点, 在
上,且位于点两侧,连接,,分别与交于点,,连接, .
(1)求证: ;
证明: 直线与相切于点 ,
,
.
是 的直径,
,
,
.
(2)若的半径,,,求 的长.
[答案] ,, .
, .
又, ,
, 是等腰直角三角形,
, .
连接 ,
是的直径, ,
.
, ,
.
又 ,
,
,即 ,
.
例2 [2024福州质检] 如图,在中,,为上一点.以为圆心,
长为半径的过点,交于另一点.若是的中点,求证:是 的切线.
证明:如图,连接, .
,
是直径,
.
是 的中点,
.
又 ,
,
,
,
.
又 点为半径的外端点,是 的切线.
例3 [2024自贡中考] 在中, ,是 的内切圆,
切点分别为,, .
图(1)
(1)图(1)中三组相等的线段分别是, ___,
____;若,,则 的半径长为___.
1
图(1)
解法提示:如图(1),连接,,设 的半径
为 ,
是 的内切圆,
,, .
在四边形中, ,
四边形 为矩形.
又 ,
四边形 为正方形,
,, .
在中,由勾股定理得 ,
,即 ,
解得 .
图(1)
(2)如图(2),延长到点,使,过点作 于点
.求证:是 的切线.
图(2)
图(2)
证明:如图(2),过点作于点 ,连接
,, .
,, ,
,
.
,
,即 .
在四边形中, ,
四边形 为矩形.
又 ,
四边形 为正方形,
, .
,
四边形 是矩形,
,
,即是 的半径.
,
是 的切线.
图(2)
解题通法
证明切线常用的两种方法
1.“有公共点,连半径,证垂直”.如果已知圆与直线有公共点,只要证明圆心与公
共点的连线与已知直线垂直即可.
2.“无公共点,作垂线,证半径”.如果已知条件中没有给出直线与圆存在公共点,
应过圆心向这条直线作垂线,然后证明垂线段的长度等于半径即可.
命题点1 切线的性质与判定[8年8考]
(第1题)
1.[2024福建中考,7] 如图,已知点,在 上,
,直线与相切,切点为,且为 的中点,
则 等于( )
A
A. B. C. D.
(第2题图)
2.[2023福州质检] 如图,中,是上一点,以 为圆
心,长为半径作半圆,与相切于点.若 ,
,则 的度数是( )
B
A. B. C. D.
(第3题)
3.[2021福建中考,9] 如图,为的直径,点在
的延长线上,,与相切,切点分别为, .若
,,则 等于( )
D
A. B. C. D.
4.[2024漳州质检] 如图,是的直径,点在上,交于点 ,
为 的切线.
(1)求证: ;
证明:如图,连接 .
是 的切线,
.
是 的直径,
.
,
,
.
又 ,
.
,
,
.
(2)若,,求 的值.
[答案] 由(1)知 , ,
.
, ,
,
.
, ,
,
,
,
.
5.[2023福建中考,21] 如图,已知内接于,的延长线交 于
点,交于点,交的切线于点,且 .
(1)求证: ;
证明:是 的切线,
,即 .
是 的直径,
,
.
,
,
,即 ,
.
(2)求证:平分 .
证明:与都是 所对的圆周角,
.
,
,
.
由(1)知, ,
,
平分 .
6.[2024泉州质检] 如图,是的直径,点在半径上,点在
上,,连接并延长至点,使得,与 的另一个交
点为 .
(1)求证:与 相切;
证明:, .
又, .
, .
是的直径, ,
, ,
,
.
又是的半径,与 相切.
(2)若,,求 的长.
[答案] 与都是 所对的圆周角,
.
在中, .
设,则, ,
,解得 .
经检验, 是原分式方程的解,
, .
在中,由勾股定理,得 ,
.
不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这
种思想得到了圆周率 的近似值为.如图, 的半径为1,运用“割
圆术”,以圆内接正六边形面积近似估
计的面积,可得 的估计值为 ,若用圆内接正十二边形作近似估计,
可得 的估计值为( )
命题点2 正多边形与圆的相关计算[18年1考]
7.[2023福建中考,10] 我国魏晋时期数学家刘徽在“九章算术注”
中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方
法来近似估算,指出“割之弥细,所失弥少,割之又割,以至于
C
A. B. C.3 D.
同课章节目录
