2025年中考数学一轮复习 -第六章 圆-第三节 与圆有关的计算 课件(共39张PPT)
文档属性
| 名称 | 2025年中考数学一轮复习 -第六章 圆-第三节 与圆有关的计算 课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 13:38:38 | ||
图片预览










文档简介
(共39张PPT)
第六章 圆
第一部分 中考考点梳理
第三节 与圆有关的计算
2025年中考数学一轮复习
考点梳理
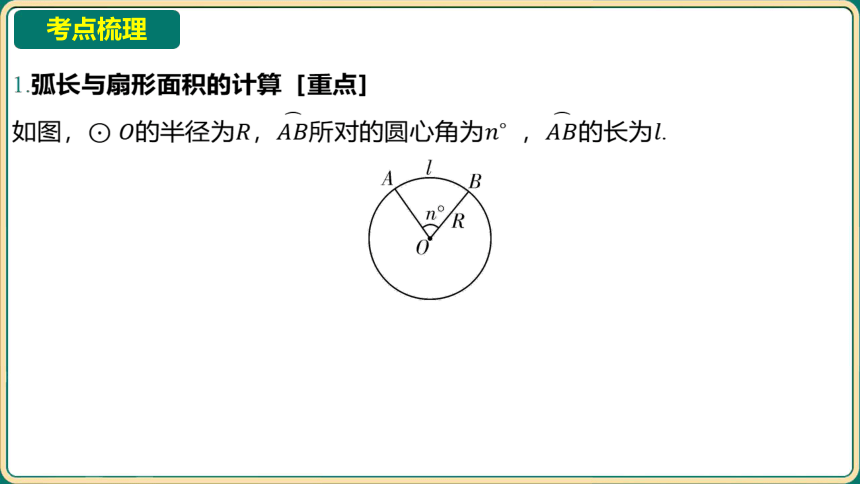
1.弧长与扇形面积的计算[重点]
如图,的半径为,所对的圆心角为 ,的长为 .
_____;
____
_____;
_ ____
弧长公式
面积公式
【解题通法】 运用弧长公式、扇形的面积公式计算时的技巧
①计算弧长必须具备两个条件——半径和该弧所对的圆心角的度数.
②当已知弧长或扇形的面积,求半径或圆心角度数时,可将弧长公式、扇形的
面积公式当作方程用.
③当已知半径
回练课本
图(1)
1.(1)如图(1),当直径为的圆形转动轮转 时,
传送带上的物体平移的距离是_____ .
图(2)
(2)如图(2),从一块直径为 的圆形铁皮上剪出一个圆心
角为 的扇形(阴影部分),则此扇形的面积为____ .
2.圆锥的相关计算
如图,圆锥的侧面展开图是扇形,圆锥的高为 ,底面圆
的半径为,母线长为 ,侧面展开图(扇形)的圆心角
为 ,弧长为 .
(1)圆锥底面圆的面积,周长 .
(2)圆锥侧面展开图(扇形)的圆心角度数 .
(3)圆锥的高、底面圆的半径和母线长之间的关系: ⑤____.
(4)圆锥的母线长等于其侧面展开图(扇形)的半径,圆锥底面圆的周长
等于其侧面展开图(扇形)的弧长.
2.(1)底面半径为3,母线长为4的圆锥的侧面积为_____.
(2)用半径为50,圆心角为 的扇形纸片围成一个圆锥的侧面,则这个
圆锥底面圆的半径为___.
(3)若圆锥的底面半径为5,高为12,则它的侧面展开图的面积是_____.
回练课本
3.阴影部分面积的计算[难点]
(1)弓形面积的求法
类型 劣弧对应的弓形 优弧对应的弓形
图形 ________________________________ ________________________________
面积计算
(2)不规则图形面积的计算方法
①分割求和(差)法:把图形适当分割,将不规则的阴影部分的面积转化成
几个规则图形面积的和或差.如图(1), .
图(1)
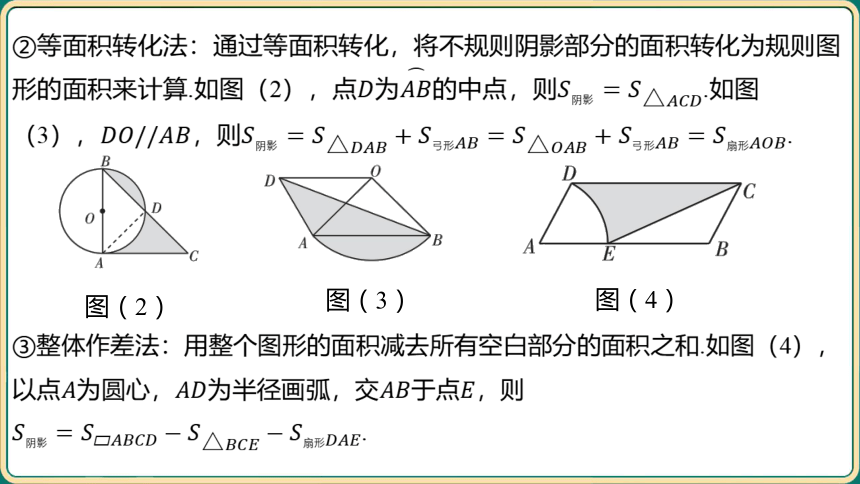
②等面积转化法:通过等面积转化,将不规则阴影部分的面积转化为规则图
形的面积来计算.如图(2),点为的中点,则 .如图
(3),,则 .
图(3)
图(4)
③整体作差法:用整个图形的面积减去所有空白部分的面积之和.如图(4),
以点为圆心,为半径画弧,交于点 ,则
.
图(2)
【提分指南】 图形中出现圆弧时,一般要先找到这条弧所在圆的圆心,常
作的辅助线是连接圆心和弧的两端点(构造半径)将其补全为扇形,再利用
图形间的关系进行求解.
图(1)
3.(1)如图(1),以等边三角形的一边 为直径的半圆
交于点,交于点,若 ,则阴影部分的面积之
和是____.
图(2)
(2)如图(2),在矩形中,分别以点和为圆心, 长
为半径画弧,两弧有且仅有一个公共点.若 ,则图中阴影
部分的面积为____________.
回练课本
(3)如图(3),在半径为1的扇形中, ,以 为直径作半
圆,交于点,连接 ,则图中阴影部分的面积之和是______.
图(3)
考法1 弧长的计算
例1 如图,在中,,以为直径的交于点 ,
,垂足为 .
(1)求证:是 的切线;
证明:如图,连接 .
,
.
,
,
,
,
.
,
,
.
又是 的半径,
是 的切线.
(2)若 ,,求 的长.
[答案] 如图,连接 .
是 的直径,
.
在中, , ,
,
,
.
, ,
,
,
.
考法2 阴影部分面积的计算
例2 如图,在矩形中,,,以点为圆心, 的长为半径
作交于点,以点为圆心,的长为半径作交于点 ,则图中阴影部
分的面积为_ _______.
(例2)
解法提示:连接,根据题意得,, .在
中, ,
,. 在
中,, , ,
,
.
例3 [2024威海中考改编] 如图,在扇形中, ,点是
的中点,过点作交于点,过点作,垂足为点 ,连
接.若 ,则阴影部分的面积为__.
(例3)
例4 [2024临沂中考] 如图,在四边形 中,
, ,.以点
为圆心,以为半径作交于点,以点 为圆
心,以为半径作交于点,连接交 于另
一点,连接 .
(1)求证:为 所在圆的切线;
证明:如图,连接 .
由题意知,, ,
, .
又,即 ,
四边形 是平行四边形,
.
又 ,
是等边三角形, .
, ,
,
在以 为直径的圆上,
.
又为 所在圆的半径,
为 所在圆的切线.
(2)求图中阴影部分面积.(结果保留 )
[答案] 如图,过点作于点 .
在中,, ,
.
由(1)知,, ,
,
.
,, .
由(1)易知 ,
.
又 ,
,
.
命题点1 弧长的计算[8年2考]
(第1题)
1.[2024三明质检] 为半圆的直径,现将一块含
角的直角三角板如图放置, 角的顶点 在半圆上,斜
边经过点,一条直角边交半圆于点.若,则
的长为( )
C
A. B. C. D.
2.[2024莆田质检] 如图,四边形内接于,为的直径,
平分,若,,则的长为___ .
(第2题)
3.[2022福建中考,21] 如图,内接于,交
于点,交于点,交于点,连接, .
(1)求证: ;
证明:, ,
四边形 是平行四边形,
.
又, ,
,
.
(2)若的半径为3, ,求的长.(结果保留 )
[答案] 如图,连接, .
由(1)得 .
又 ,
,
,
的长为 .
4.[2023泉州质检] 如图,是的外接圆,,直径交 于
点 .
(1)求证: ;
证明:如图,连接, .
,
,, .
,
,
,
,
,
.
(2)若 ,,求 的长.
[答案] 如图, ,
,
,
.
,
是等边三角形,
,
的长为 .
命题点2 扇形及不规则图形面积的计算[8年2考]
5.[2020福建中考,13] 一个扇形的圆心角是 ,半径为4,则这个扇形的面积
为____.(结果保留 )
(第6题)
6.[2022莆田质检] 如图,方格纸中2个小正方形的边长均
为1,图中阴影部分均为扇形,则这两个小扇形的面积之
和为__.(结果保留 )
(第7题)
7.[2024龙岩质检改编] 如图,,是半径为6的半圆 上的
两个点,是直径,,若的长度为 ,则图
中阴影部分的面积为____.
新课标 新考向
【新课标·综合与实践】[2024广东中考]
【主题】滤纸与漏斗.
图(1)
【素材】如图(1)所示:
①一张直径为 的圆形滤纸;
②一只漏斗口直径与母线均为 的圆锥形过滤漏斗.
【实践操作】
步骤1:取一张滤纸;
步骤2:按如图(2)所示步骤折叠好滤纸;
步骤3:将其中一层撑开,围成圆锥形;
步骤4:将围成圆锥形的滤纸放入如图(1)所示漏斗中.
图(2)
【实践探索】
(1)滤纸是否能紧贴此漏斗内壁(忽略漏斗管口处) 用你所学的数学知识
说明.
[答案] 滤纸能紧贴此漏斗内壁.
理由:如图,设大圆锥的顶点为,小圆锥的顶点为,连接, .
直径为10的圆形滤纸的周长为 ,
小圆锥底面圆的周长为 ,
.
由题意知 ,
,
是等边三角形.
,
是等边三角形,
滤纸能紧贴此漏斗内壁.
(2)当滤纸紧贴漏斗内壁时,求滤纸围成圆锥形的体积.(结果保留 )
[答案] 由题意可得滤纸围成的圆锥形的高为 ,
滤纸围成圆锥形的体积为 .
第六章 圆
第一部分 中考考点梳理
第三节 与圆有关的计算
2025年中考数学一轮复习
考点梳理
1.弧长与扇形面积的计算[重点]
如图,的半径为,所对的圆心角为 ,的长为 .
_____;
____
_____;
_ ____
弧长公式
面积公式
【解题通法】 运用弧长公式、扇形的面积公式计算时的技巧
①计算弧长必须具备两个条件——半径和该弧所对的圆心角的度数.
②当已知弧长或扇形的面积,求半径或圆心角度数时,可将弧长公式、扇形的
面积公式当作方程用.
③当已知半径
回练课本
图(1)
1.(1)如图(1),当直径为的圆形转动轮转 时,
传送带上的物体平移的距离是_____ .
图(2)
(2)如图(2),从一块直径为 的圆形铁皮上剪出一个圆心
角为 的扇形(阴影部分),则此扇形的面积为____ .
2.圆锥的相关计算
如图,圆锥的侧面展开图是扇形,圆锥的高为 ,底面圆
的半径为,母线长为 ,侧面展开图(扇形)的圆心角
为 ,弧长为 .
(1)圆锥底面圆的面积,周长 .
(2)圆锥侧面展开图(扇形)的圆心角度数 .
(3)圆锥的高、底面圆的半径和母线长之间的关系: ⑤____.
(4)圆锥的母线长等于其侧面展开图(扇形)的半径,圆锥底面圆的周长
等于其侧面展开图(扇形)的弧长.
2.(1)底面半径为3,母线长为4的圆锥的侧面积为_____.
(2)用半径为50,圆心角为 的扇形纸片围成一个圆锥的侧面,则这个
圆锥底面圆的半径为___.
(3)若圆锥的底面半径为5,高为12,则它的侧面展开图的面积是_____.
回练课本
3.阴影部分面积的计算[难点]
(1)弓形面积的求法
类型 劣弧对应的弓形 优弧对应的弓形
图形 ________________________________ ________________________________
面积计算
(2)不规则图形面积的计算方法
①分割求和(差)法:把图形适当分割,将不规则的阴影部分的面积转化成
几个规则图形面积的和或差.如图(1), .
图(1)
②等面积转化法:通过等面积转化,将不规则阴影部分的面积转化为规则图
形的面积来计算.如图(2),点为的中点,则 .如图
(3),,则 .
图(3)
图(4)
③整体作差法:用整个图形的面积减去所有空白部分的面积之和.如图(4),
以点为圆心,为半径画弧,交于点 ,则
.
图(2)
【提分指南】 图形中出现圆弧时,一般要先找到这条弧所在圆的圆心,常
作的辅助线是连接圆心和弧的两端点(构造半径)将其补全为扇形,再利用
图形间的关系进行求解.
图(1)
3.(1)如图(1),以等边三角形的一边 为直径的半圆
交于点,交于点,若 ,则阴影部分的面积之
和是____.
图(2)
(2)如图(2),在矩形中,分别以点和为圆心, 长
为半径画弧,两弧有且仅有一个公共点.若 ,则图中阴影
部分的面积为____________.
回练课本
(3)如图(3),在半径为1的扇形中, ,以 为直径作半
圆,交于点,连接 ,则图中阴影部分的面积之和是______.
图(3)
考法1 弧长的计算
例1 如图,在中,,以为直径的交于点 ,
,垂足为 .
(1)求证:是 的切线;
证明:如图,连接 .
,
.
,
,
,
,
.
,
,
.
又是 的半径,
是 的切线.
(2)若 ,,求 的长.
[答案] 如图,连接 .
是 的直径,
.
在中, , ,
,
,
.
, ,
,
,
.
考法2 阴影部分面积的计算
例2 如图,在矩形中,,,以点为圆心, 的长为半径
作交于点,以点为圆心,的长为半径作交于点 ,则图中阴影部
分的面积为_ _______.
(例2)
解法提示:连接,根据题意得,, .在
中, ,
,. 在
中,, , ,
,
.
例3 [2024威海中考改编] 如图,在扇形中, ,点是
的中点,过点作交于点,过点作,垂足为点 ,连
接.若 ,则阴影部分的面积为__.
(例3)
例4 [2024临沂中考] 如图,在四边形 中,
, ,.以点
为圆心,以为半径作交于点,以点 为圆
心,以为半径作交于点,连接交 于另
一点,连接 .
(1)求证:为 所在圆的切线;
证明:如图,连接 .
由题意知,, ,
, .
又,即 ,
四边形 是平行四边形,
.
又 ,
是等边三角形, .
, ,
,
在以 为直径的圆上,
.
又为 所在圆的半径,
为 所在圆的切线.
(2)求图中阴影部分面积.(结果保留 )
[答案] 如图,过点作于点 .
在中,, ,
.
由(1)知,, ,
,
.
,, .
由(1)易知 ,
.
又 ,
,
.
命题点1 弧长的计算[8年2考]
(第1题)
1.[2024三明质检] 为半圆的直径,现将一块含
角的直角三角板如图放置, 角的顶点 在半圆上,斜
边经过点,一条直角边交半圆于点.若,则
的长为( )
C
A. B. C. D.
2.[2024莆田质检] 如图,四边形内接于,为的直径,
平分,若,,则的长为___ .
(第2题)
3.[2022福建中考,21] 如图,内接于,交
于点,交于点,交于点,连接, .
(1)求证: ;
证明:, ,
四边形 是平行四边形,
.
又, ,
,
.
(2)若的半径为3, ,求的长.(结果保留 )
[答案] 如图,连接, .
由(1)得 .
又 ,
,
,
的长为 .
4.[2023泉州质检] 如图,是的外接圆,,直径交 于
点 .
(1)求证: ;
证明:如图,连接, .
,
,, .
,
,
,
,
,
.
(2)若 ,,求 的长.
[答案] 如图, ,
,
,
.
,
是等边三角形,
,
的长为 .
命题点2 扇形及不规则图形面积的计算[8年2考]
5.[2020福建中考,13] 一个扇形的圆心角是 ,半径为4,则这个扇形的面积
为____.(结果保留 )
(第6题)
6.[2022莆田质检] 如图,方格纸中2个小正方形的边长均
为1,图中阴影部分均为扇形,则这两个小扇形的面积之
和为__.(结果保留 )
(第7题)
7.[2024龙岩质检改编] 如图,,是半径为6的半圆 上的
两个点,是直径,,若的长度为 ,则图
中阴影部分的面积为____.
新课标 新考向
【新课标·综合与实践】[2024广东中考]
【主题】滤纸与漏斗.
图(1)
【素材】如图(1)所示:
①一张直径为 的圆形滤纸;
②一只漏斗口直径与母线均为 的圆锥形过滤漏斗.
【实践操作】
步骤1:取一张滤纸;
步骤2:按如图(2)所示步骤折叠好滤纸;
步骤3:将其中一层撑开,围成圆锥形;
步骤4:将围成圆锥形的滤纸放入如图(1)所示漏斗中.
图(2)
【实践探索】
(1)滤纸是否能紧贴此漏斗内壁(忽略漏斗管口处) 用你所学的数学知识
说明.
[答案] 滤纸能紧贴此漏斗内壁.
理由:如图,设大圆锥的顶点为,小圆锥的顶点为,连接, .
直径为10的圆形滤纸的周长为 ,
小圆锥底面圆的周长为 ,
.
由题意知 ,
,
是等边三角形.
,
是等边三角形,
滤纸能紧贴此漏斗内壁.
(2)当滤纸紧贴漏斗内壁时,求滤纸围成圆锥形的体积.(结果保留 )
[答案] 由题意可得滤纸围成的圆锥形的高为 ,
滤纸围成圆锥形的体积为 .
同课章节目录
