2025年中考数学一轮复习 -第七章 图形与变换-第三节 图形的对称与折叠 课件(共26张PPT)

(共26张PPT)
第七章 图形与变换
第一部分 中考考点梳理
第三节 图形的对称与折叠
2025年中考数学一轮复习
考点梳理
1.轴对称图形与轴对称［基础点］
（1）轴对称图形与轴对称
轴对称图形 轴对称
定义 如果把一个平面图形沿一条直线 折叠，直线两旁的部分能够互相 重合，那么这个图形就叫做 ①____________，这条直线就是 它的②________. 把一个图形沿着某一条直线折
叠，如果它能够与另一个图形重
合，那么就说这两个图形成轴对
称，这条直线叫做③________.
轴对称图形
对称轴
对称轴
轴对称图形 轴对称
图示 ___________________________________________ _____________________________________
性质 .对应线段相等，如④____, ; .对应角相等,如⑤____, ; .对应图形全等,即, ; .非重合对应点的连线被对称轴垂直平分.
轴对称图形 轴对称
区别 .轴对称图形是指具有特殊形状 的一个图形; .对称轴不一定只有一条. .轴对称是指两个全等图形之间的
位置关系;
.对称轴只有一条.
（2）作轴对称图形的一般步骤
.找:在原图形上找关键点（如线段的端点、线与线的交点等）.
.作:作各个关键点关于已知直线（对称轴）的对称点.
.连:按原图形依次连接各关键点的对称点.
回练课本
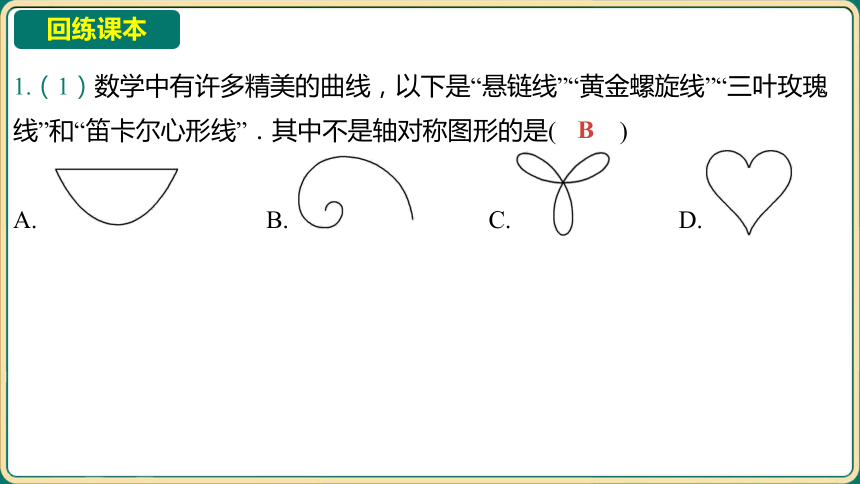
1.（1）数学中有许多精美的曲线，以下是“悬链线”“黄金螺旋线”“三叶玫瑰
线”和“笛卡尔心形线”．其中不是轴对称图形的是( )
B
A. B. C. D.
（2）如图，与关于直线 对称，则以下结论中错误的是
( )
A
A. B.
C. D.被 垂直平分
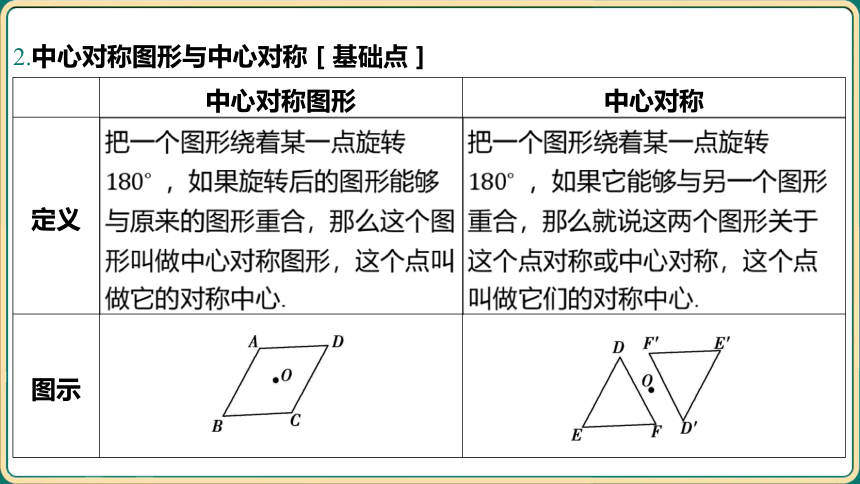
2.中心对称图形与中心对称［基础点］
中心对称图形 中心对称
定义 把一个图形绕着某一点旋转 ，如果旋转后的图形能够 与原来的图形重合，那么这个图 形叫做中心对称图形，这个点叫 做它的对称中心. 把一个图形绕着某一点旋转
，如果它能够与另一个图形
重合，那么就说这两个图形关于
这个点对称或中心对称，这个点
叫做它们的对称中心.
图示 ________________________________________ _____________________________________________
中心对称图形 中心对称
性质 （1）对应线段⑥______，如, ; （2）对应角⑦______，如, ; （3）成中心对称的两个图形，对应点所连线段均过对称中心且被 对称中心平分; （4）成中心对称的两个图形，其对应线段互相平行（或在一条直 线上）. 区别 中心对称图形是指具有特殊形状 的一个图形. 中心对称是指两个全等图形之间
的位置关系.
相等
相等
【提分指南】
常见的轴对称图形、中心对称图形
2.（1）纹样是我国古代艺术中的瑰宝.下列四幅纹样图形既是轴对称图形又
是中心对称图形的是( )
B
A. B. C. D.
（2）如图,与关于点 成中心对称，则下列
结论不成立的是( )
D
A.点与点是关于点的对称点 B.
C. D.
回练课本
3.图形的折叠［难点］
（1）位于折痕两侧的图形关于折痕成轴对称;
（2）折叠前后的两部分图形全等;
（3）折叠前后,非重合对应点的连线均被折痕所在直线垂直平分.
【提分指南】 图形折叠的本质是轴对称,解决折叠问题的关键是从折叠的性
质和原图形的性质两方面入手,寻找图形中相等的线段、相等的角,从而把折
叠问题转化为三角形的边角问题求解.
3.如图是一张矩形纸片,,为边 上一点,且
,连接,若将矩形沿对折,使得点落在边 上
的点处,则 的长为( )
C
A.8 B.7 C.6 D.5
回练课本
考法 图形的折叠
例
图（1）
（1）如图（1），在中， ，
［1］，点是斜边上一点，点为直角边 上一点，将
沿折叠，点的对应点为点 ［2］．
. .
. .
. .
①如图（2），若［3］，则____ .
75
图（2）
②如图（3），若［4］，点与点重合［5］，则 的长为____.
解法提示： ， ， .由折叠的
性质可得 ， .在 中，
.
. .
. .
. .
解题指导
图（3）
①结合［1］［2］［3］,要求的度数，可联想到在 中利用三角
形的内角和定理求解.
②结合［1］［2］［5］，可知的度数.要求 的长，再结合［4］,可
联想到在 中利用锐角三角函数求解.
（2）在矩形中,［6］,点在边上,将沿直线 折叠［7］.
①如图（4）,若点恰好落在对角线上的点处,［8］,则 的
长为___.
6
图（4）
解法提示：由折叠的性质可得,又 ,
, , .
. .
. .
. .
图（5）
②如图（5）,若,,点落在点处,交 于点
［9］,则 的长为 __.
解法提示：由折叠的性质可得 ,
, .如图,过
点作于点,则, .易证
,.又,.在 中,由
勾股定理可得, , .
. .
. .
解题指导
①由［7］可知折叠前后的对应角相等，再结合［6］［8］可求出的度
数，继而联想到在中利用锐角三角函数求的长.
②结合［6］［7］［9］可知 ，,的长.要求的长，可
联想到在中利用勾股定理求解.
提分特训
1.如图，将平行四边形折叠，使点落在边上的点 处，若
， ，则 的度数为______.
（第1题）
2.[2024牡丹江中考] 小明同学手中有一张矩形纸片， ，
，他进行了如下操作：
第一步，如图（1），将矩形纸片对折，使与重合，得到折痕 ，将
纸片展平．
（第2题）
第二步，如图（2），再一次折叠纸片，把
沿折叠得到，交折痕
于点，则线段的长为____ ．
3.如图,菱形的边长为4, ,将菱形沿折叠,顶点 恰好落
在边的中点处,求 的长.
[答案] 如图，过点作,交的延长线于点 .
四边形 是菱形，
，
, .
设,则, ，
.
是 的中点，
, .
在中, ,
,
解得 ,
.
命题点 图形的对称［8年5考］
1.[2024宁德质检] 下列图案是中心对称图形的是( )
D
A. B. C. D.
2.[2022福建中考，4] 美术老师让同学们设计窗花,下列作品为轴对称图形的
是( )
A
A. B. C. D.
（第3题）
3.[2024三明质检] 瓷器上的纹饰是我国古代传统文化的重要载
体之一,如图所示的图形是某瓷器上的纹饰,该图形是轴对称图形,
其对称轴的条数为( )
C
A.1 B.2 C.4 D.8
4.[2024福建中考，9] 小明用两个全等的等腰三角形设计了一个“蝴蝶”的平
面图案，如图.其中与都是等腰三角形，且它们关于直线 对称，
点,分别是底边,的中点， .下列推断错误的是( )
B
（第4题）
A. B.
C. D.