2025年中考数学一轮复习 -第七章 图形与变换-第四节 图形的平移、旋转与位似 课件(共48张PPT)
文档属性
| 名称 | 2025年中考数学一轮复习 -第七章 图形与变换-第四节 图形的平移、旋转与位似 课件(共48张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-12 12:44:57 | ||
图片预览









文档简介
(共48张PPT)
第七章 图形与变换
第一部分 中考考点梳理
第四节 图形的平移、旋转与位似
2025年中考数学一轮复习
考点梳理
1.图形的平移与旋转[重点]
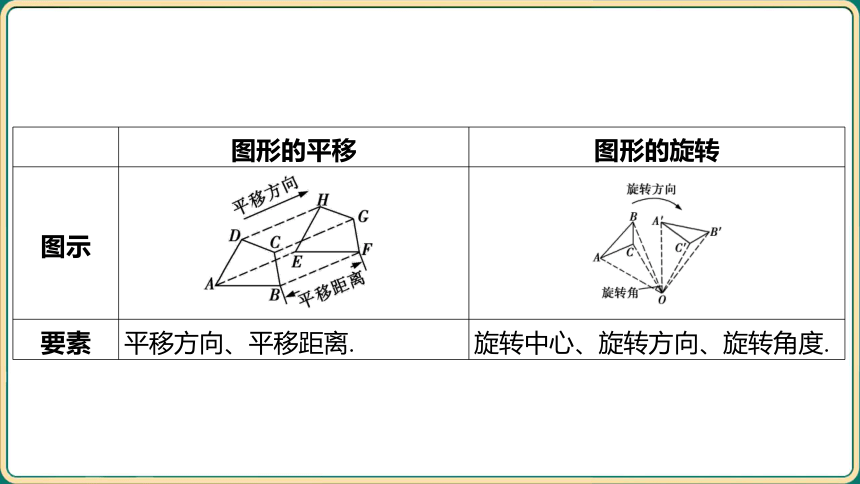
图形的平移 图形的旋转
定义 把一个图形整体沿某一直线方 向移动,会得到一个新的图 形,新图形与原图形的形状和 大小完全相同,图形的这种移 动叫做平移. 把一个平面图形绕着平面内某一
点 转动一定角度叫做图形的旋
转,点 叫做旋转中心,转动的
角叫做旋转角.
图形的平移 图形的旋转
图示 _______________________________________________ ______________________________________
要素 平移方向、平移距离. 旋转中心、旋转方向、旋转角度.
图形的平移 图形的旋转
性质 (1)平移不改变图形的大小和 形状,只改变图形的位置,平 移前后的两图形①______; (2)对应点所连线段平行 (或在一条直线上)且相等. (1)旋转前后的图形②______;
(2)对应点到旋转中心的距离③
______;
(3)对应点与旋转中心所连线段
的夹角④______旋转角.
全等
全等
相等
等于
图形的平移 图形的旋转
网格作 图步骤 (1)根据题意,确定平移的方 向和平移距离; (2)找出原图形的关键点; (3)按平移方向和平移距离平 移各个关键点,得到各关键点 的对应点; (4)按原图形依次连接各关键 点的对应点,得到平移后的图 形. (1)根据题意,确定旋转中心、
旋转方向及旋转角度;
(2)找出原图形的关键点;
(3)连接关键点与旋转中心,按
旋转方向与旋转角将关键点旋
转,得到各关键点的对应点;
(4)按原图形依次连接各关键点
的对应点,得到旋转后的图形.
【解题通法】 与旋转有关的常见试题及解题方法
①探索在旋转过程中图形位置的变化和线段、角度的数量关系:首先注意旋
转中心、旋转方向和旋转角度,注意旋转前后的对应点、对应边、对应角,利
用旋转前后的不变性进行探索.
②计算在旋转过程中某点经过的路径:这类试题实质上是求旋转中心与该点
连线的线段在旋转过程中形成的扇形的弧长.
③计算在旋转过程中某线段扫过的面积:先确定旋转中心(圆心)的位置及
旋转线段的长度(半径),结合旋转角度,利用扇形面积公式计算相应的扇形
面积,有时也需要用到割补法.
回练课本
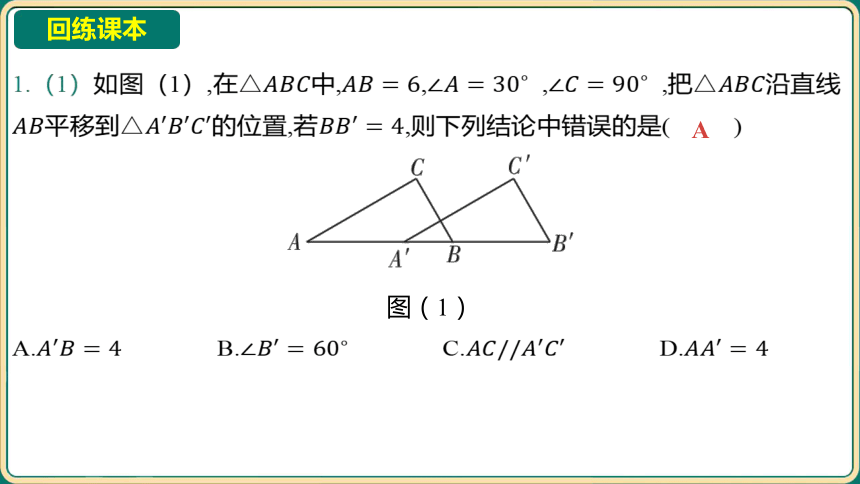
1.(1)如图(1),在中,, , ,把 沿直线
平移到的位置,若 ,则下列结论中错误的是( )
A
图(1)
A. B. C. D.
图(2)
(2)如图(2),现有一把直尺和一块三角尺,其中
, ,,点 对应直尺的刻度
为12.将该三角尺沿着直尺边缘平移,使得 移动到
的位置,点对应直尺的刻度为0,则四边形
的面积是( )
B
A.96 B. C.192 D.
图(3)
(3)如图(3), 在中, , ,
,将绕点逆时针旋转得到 ,当点
落在边上时,连接,则 的长度是( )
B
A. B. C. D.
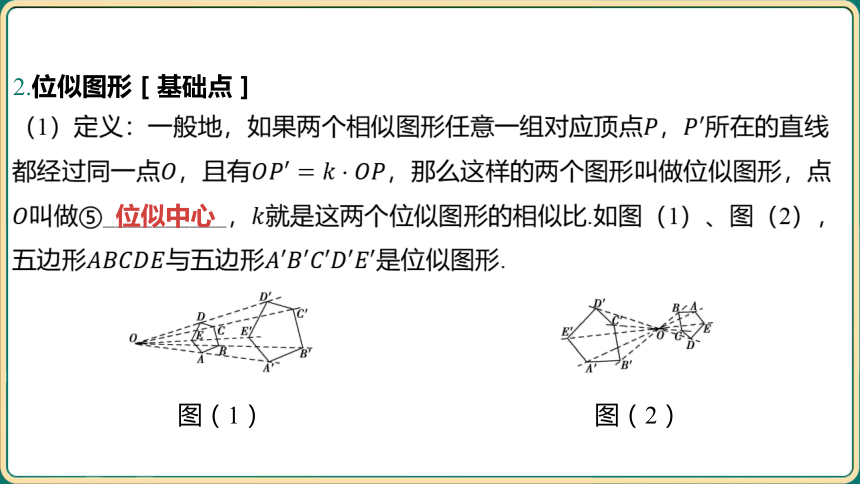
2.位似图形[基础点]
(1)定义:一般地,如果两个相似图形任意一组对应顶点, 所在的直线
都经过同一点,且有 ,那么这样的两个图形叫做位似图形,点
叫做⑤__________, 就是这两个位似图形的相似比.如图(1)、图(2),
五边形与五边形 是位似图形.
位似中心
图(1)
图(2)
(2)性质: .任意一组对应点的连线所在直线都相交于同一点(位似中心);
.位似图形对应边互相平行或在同一条直线上,且成比例;
.位似图形上任意一对对应点到位似中心的距离之比等于⑥________,位似
图形的面积比等于⑦______________;
.位似图形是特殊的相似图形,具有相似图形的一切性质.
相似比
相似比的平方
(3)在网格中作位似图形的步骤:
.确定位似中心;
.连接位似中心和原图的关键点确定各关键点的对应点所在的直线;
.根据相似比,确定关键点的对应点;
.顺次连接各对应点,得到放大或缩小的图形.
【注意】 两个位似图形可能位于位似中心的两侧,也可能位于位似中心的
同侧,位似中心只有一个.
2.(1)如图,在平面直角坐标系中,的顶点为 ,
,.以点为位似中心,在第三象限内作与 的
相似比为的位似图形,则点 的坐标为( )
B
A. B. C. D.
(2)在平面直角坐标系中,点,的坐标分别为, .以原点
为位似中心,将缩小为原来的一半,得到,则点的对应点 的坐
标是________________.
或
回练课本
考法1 图形平移的性质及相关计算
图(1)
例1 如图(1),在中, ,
, .将在直线 上向右
平移得到,连接 .
(1)四边形的形状是____________,四边形 的形状是______.
(2)若,相交于点,四边形的面积是,则四边形 的
面积为____ .
平行四边形
矩形
10
解法提示:由平移可知,
,
, ,
.
图(2)
(3)将向右平移___ ,才能使四边形
是正方形;将向右平移____ ,才
能使四边形 是菱形.
6
12
(4)如图(2),若点与点 重合,则
①扫过的面积为______ ;
[解析] 解法提示:由平移易得,扫过的面积矩形 的面积
的面积
.
②四边形的周长为_____________ .
解法提示:由题易知, ,
, 四边形 的周长
.
(5)若向右移动的速度是,设移动时间为,四边形
的面积为.求关于 的函数关系式.
[答案] 由题意易知,,四边形
始终为直角梯形,
,
关于的函数关系式是 .
考法2 图形旋转的性质及相关计算
例2 将绕某一点逆时针旋转一定角度后得到 ,其中
点,的对应点分别是点, .
图(1)
(1)如图(1),点在边上,延长交于点, ,
交于点, .
①旋转中心为_____,旋转角最小为____ .
点
90
② 的形状是________________.
等腰直角三角形
③求证: .
证明:由旋转可得 ,
, ,
, .
④求证: .
证明:由旋转可得,, ,
,, ,
, .
, ,
,即 .
图(1)
图(2)
(2)如图(2), , , .
若,分别与,交于点, ,则线段
的长为_________.
解法提示:由旋转可知, ,
, ,
, , 在
中,
, .
, , .
提分特训
点,分别在正方形的边,上, .
(1)如图(1),将绕点顺时针旋转 ,得到,若 ,则四
边形 的面积为___;
9
(2)如图(2),连接,分别交,于点,,求证: .
证明:是正方形 的对角线,
,, .
图(2)
如图,将绕点顺时针旋转 ,得到 ,连接
,
,, ,
,
,
.
, ,
.
, ,
,
,
.
命题点1 图形的平移及相关计算[8年3考]
1.[2024泉州质检] 如图,在矩形中, ,
,将沿着射线的方向,平移线段 的
长度得到,则四边形 的周长为( )
B
A.16 B.20 C.24 D.40
2.[2024龙岩质检] 如图,将沿射线 方向平移得到
,,,的对应点分别是,, .
(1)若 ,求 的度数;
[答案] 由平移的性质得, ,
四边形 是平行四边形,
.
(2)若,当时,求 的长.
[答案] 由平移的性质得 .
又 ,
.
3.[2021福建中考,21] 如图,在 中,
.线段是由线段平移得到的,点 在
边上,是以 为斜边的等腰直角三角形,且
点恰好在 的延长线上.
(1)求证: ;
证明:在等腰直角三角形中, ,
.
,
,
.
(2)求证: .
[答案] 如图,连接 .
由平移可知,, .
,
.
是等腰直角三角形,
.
由(1)得 ,
,
,
.
命题点2 图形的旋转及相关计算[8年6考]
(第4题)
4.[2024厦门质检] 如图,将绕点 顺时针旋转至
.下列角中,是旋转角的是( )
A
A. B. C. D.
(第5题)
5.[2024宁德质检] 如图,将绕着点 顺时针旋转
得到,点的对应点落在边上,且,,
三点共线,则下列结论错误的是( )
A
A. B.
C. D.
6.[2024莆田质检] 如图,在中, ,,点在
边上,连接.把线段绕点逆时针旋转 得到线段,将 沿
直线翻折得到,直线与直线交于点 .
备用图
(1)请补全图形,找出与 相等的线段,并说明理由;
[答案] 补全图形如图(1)所示.
图(1)
.
理由: ,
.
由折叠知, ,
, .
又, ,
,
.
图(1)
(2)若为的三等分点,求 的值.
[答案] 当时,如图(1)所示,连接 .
,, .
由(1)得, , ,
.
,, ,
,
, ,
.
图(1)
又 ,
, .
设,,,则 .
在中, ,
即,解得 ,
.
图(1)
当时,如图(2)所示,连接 .
图(2)
同理可设,,, ,
则 .
在中,,
即 ,
解得 ,
.
综上所述,或 .
新课标 新考向
【新课标·综合与实践】问题情境:数学活动课上,老师要求同学们以矩形
为背景探索几何图形运动变化中的数学结论.如图(1),在矩形 中,
为对角线的中点,连接.点在边上,且,线段 的延
长线交于点 .
猜想证明:
(1)“笃学”小组发现 ,请你证明这一结论.
证明:如图(1).
图(1)
四边形 是矩形,
, ,
.
为 的中点,
.
,
,
.
,
.
图(1)
操作探究:
(2)“勤思”小组将图(1)中的绕点顺时针旋转(设点, 的对应
点分别为,, ),在认真分析旋转到不同位置时的情
形后,提出如下问题,请你解答:
图(1)
①如图(2),当点落在的延长线上时,连接,判断四边形 的
形状,并说明理由;
图(2)
[答案] 四边形 为菱形.
理由如下:
如图(2),由旋转得,, .
图(2)
四边形 为矩形,
,
,
, ,
.
.
,
,
,
.
由(1)得 ,
,
四边形 是菱形.
图(2)
②若,,当线段所在直线与 所在直线垂直时,直接写
出, 两点间的距离.
[答案] ,两点间的距离为或 .
解法提示:在中, ,, ,
,, .
为的中点, .
图(3)
当将绕点顺时针旋转 时,点的对应点
落在线段上,此时,如图(3),过点
作,交的延长线于点,连接 .
由旋转可知,, .
又 ,
,
,,, ,
, .
图(4)
当顺时针旋转 时,点的对应点落在线段 的
延长线上,此时,如图(4),过点作 ,
垂足为点,连接 .
由旋转可知,, .
又 , ,
,,, ,
, .
综上,,两点间的距离为或 .
第七章 图形与变换
第一部分 中考考点梳理
第四节 图形的平移、旋转与位似
2025年中考数学一轮复习
考点梳理
1.图形的平移与旋转[重点]
图形的平移 图形的旋转
定义 把一个图形整体沿某一直线方 向移动,会得到一个新的图 形,新图形与原图形的形状和 大小完全相同,图形的这种移 动叫做平移. 把一个平面图形绕着平面内某一
点 转动一定角度叫做图形的旋
转,点 叫做旋转中心,转动的
角叫做旋转角.
图形的平移 图形的旋转
图示 _______________________________________________ ______________________________________
要素 平移方向、平移距离. 旋转中心、旋转方向、旋转角度.
图形的平移 图形的旋转
性质 (1)平移不改变图形的大小和 形状,只改变图形的位置,平 移前后的两图形①______; (2)对应点所连线段平行 (或在一条直线上)且相等. (1)旋转前后的图形②______;
(2)对应点到旋转中心的距离③
______;
(3)对应点与旋转中心所连线段
的夹角④______旋转角.
全等
全等
相等
等于
图形的平移 图形的旋转
网格作 图步骤 (1)根据题意,确定平移的方 向和平移距离; (2)找出原图形的关键点; (3)按平移方向和平移距离平 移各个关键点,得到各关键点 的对应点; (4)按原图形依次连接各关键 点的对应点,得到平移后的图 形. (1)根据题意,确定旋转中心、
旋转方向及旋转角度;
(2)找出原图形的关键点;
(3)连接关键点与旋转中心,按
旋转方向与旋转角将关键点旋
转,得到各关键点的对应点;
(4)按原图形依次连接各关键点
的对应点,得到旋转后的图形.
【解题通法】 与旋转有关的常见试题及解题方法
①探索在旋转过程中图形位置的变化和线段、角度的数量关系:首先注意旋
转中心、旋转方向和旋转角度,注意旋转前后的对应点、对应边、对应角,利
用旋转前后的不变性进行探索.
②计算在旋转过程中某点经过的路径:这类试题实质上是求旋转中心与该点
连线的线段在旋转过程中形成的扇形的弧长.
③计算在旋转过程中某线段扫过的面积:先确定旋转中心(圆心)的位置及
旋转线段的长度(半径),结合旋转角度,利用扇形面积公式计算相应的扇形
面积,有时也需要用到割补法.
回练课本
1.(1)如图(1),在中,, , ,把 沿直线
平移到的位置,若 ,则下列结论中错误的是( )
A
图(1)
A. B. C. D.
图(2)
(2)如图(2),现有一把直尺和一块三角尺,其中
, ,,点 对应直尺的刻度
为12.将该三角尺沿着直尺边缘平移,使得 移动到
的位置,点对应直尺的刻度为0,则四边形
的面积是( )
B
A.96 B. C.192 D.
图(3)
(3)如图(3), 在中, , ,
,将绕点逆时针旋转得到 ,当点
落在边上时,连接,则 的长度是( )
B
A. B. C. D.
2.位似图形[基础点]
(1)定义:一般地,如果两个相似图形任意一组对应顶点, 所在的直线
都经过同一点,且有 ,那么这样的两个图形叫做位似图形,点
叫做⑤__________, 就是这两个位似图形的相似比.如图(1)、图(2),
五边形与五边形 是位似图形.
位似中心
图(1)
图(2)
(2)性质: .任意一组对应点的连线所在直线都相交于同一点(位似中心);
.位似图形对应边互相平行或在同一条直线上,且成比例;
.位似图形上任意一对对应点到位似中心的距离之比等于⑥________,位似
图形的面积比等于⑦______________;
.位似图形是特殊的相似图形,具有相似图形的一切性质.
相似比
相似比的平方
(3)在网格中作位似图形的步骤:
.确定位似中心;
.连接位似中心和原图的关键点确定各关键点的对应点所在的直线;
.根据相似比,确定关键点的对应点;
.顺次连接各对应点,得到放大或缩小的图形.
【注意】 两个位似图形可能位于位似中心的两侧,也可能位于位似中心的
同侧,位似中心只有一个.
2.(1)如图,在平面直角坐标系中,的顶点为 ,
,.以点为位似中心,在第三象限内作与 的
相似比为的位似图形,则点 的坐标为( )
B
A. B. C. D.
(2)在平面直角坐标系中,点,的坐标分别为, .以原点
为位似中心,将缩小为原来的一半,得到,则点的对应点 的坐
标是________________.
或
回练课本
考法1 图形平移的性质及相关计算
图(1)
例1 如图(1),在中, ,
, .将在直线 上向右
平移得到,连接 .
(1)四边形的形状是____________,四边形 的形状是______.
(2)若,相交于点,四边形的面积是,则四边形 的
面积为____ .
平行四边形
矩形
10
解法提示:由平移可知,
,
, ,
.
图(2)
(3)将向右平移___ ,才能使四边形
是正方形;将向右平移____ ,才
能使四边形 是菱形.
6
12
(4)如图(2),若点与点 重合,则
①扫过的面积为______ ;
[解析] 解法提示:由平移易得,扫过的面积矩形 的面积
的面积
.
②四边形的周长为_____________ .
解法提示:由题易知, ,
, 四边形 的周长
.
(5)若向右移动的速度是,设移动时间为,四边形
的面积为.求关于 的函数关系式.
[答案] 由题意易知,,四边形
始终为直角梯形,
,
关于的函数关系式是 .
考法2 图形旋转的性质及相关计算
例2 将绕某一点逆时针旋转一定角度后得到 ,其中
点,的对应点分别是点, .
图(1)
(1)如图(1),点在边上,延长交于点, ,
交于点, .
①旋转中心为_____,旋转角最小为____ .
点
90
② 的形状是________________.
等腰直角三角形
③求证: .
证明:由旋转可得 ,
, ,
, .
④求证: .
证明:由旋转可得,, ,
,, ,
, .
, ,
,即 .
图(1)
图(2)
(2)如图(2), , , .
若,分别与,交于点, ,则线段
的长为_________.
解法提示:由旋转可知, ,
, ,
, , 在
中,
, .
, , .
提分特训
点,分别在正方形的边,上, .
(1)如图(1),将绕点顺时针旋转 ,得到,若 ,则四
边形 的面积为___;
9
(2)如图(2),连接,分别交,于点,,求证: .
证明:是正方形 的对角线,
,, .
图(2)
如图,将绕点顺时针旋转 ,得到 ,连接
,
,, ,
,
,
.
, ,
.
, ,
,
,
.
命题点1 图形的平移及相关计算[8年3考]
1.[2024泉州质检] 如图,在矩形中, ,
,将沿着射线的方向,平移线段 的
长度得到,则四边形 的周长为( )
B
A.16 B.20 C.24 D.40
2.[2024龙岩质检] 如图,将沿射线 方向平移得到
,,,的对应点分别是,, .
(1)若 ,求 的度数;
[答案] 由平移的性质得, ,
四边形 是平行四边形,
.
(2)若,当时,求 的长.
[答案] 由平移的性质得 .
又 ,
.
3.[2021福建中考,21] 如图,在 中,
.线段是由线段平移得到的,点 在
边上,是以 为斜边的等腰直角三角形,且
点恰好在 的延长线上.
(1)求证: ;
证明:在等腰直角三角形中, ,
.
,
,
.
(2)求证: .
[答案] 如图,连接 .
由平移可知,, .
,
.
是等腰直角三角形,
.
由(1)得 ,
,
,
.
命题点2 图形的旋转及相关计算[8年6考]
(第4题)
4.[2024厦门质检] 如图,将绕点 顺时针旋转至
.下列角中,是旋转角的是( )
A
A. B. C. D.
(第5题)
5.[2024宁德质检] 如图,将绕着点 顺时针旋转
得到,点的对应点落在边上,且,,
三点共线,则下列结论错误的是( )
A
A. B.
C. D.
6.[2024莆田质检] 如图,在中, ,,点在
边上,连接.把线段绕点逆时针旋转 得到线段,将 沿
直线翻折得到,直线与直线交于点 .
备用图
(1)请补全图形,找出与 相等的线段,并说明理由;
[答案] 补全图形如图(1)所示.
图(1)
.
理由: ,
.
由折叠知, ,
, .
又, ,
,
.
图(1)
(2)若为的三等分点,求 的值.
[答案] 当时,如图(1)所示,连接 .
,, .
由(1)得, , ,
.
,, ,
,
, ,
.
图(1)
又 ,
, .
设,,,则 .
在中, ,
即,解得 ,
.
图(1)
当时,如图(2)所示,连接 .
图(2)
同理可设,,, ,
则 .
在中,,
即 ,
解得 ,
.
综上所述,或 .
新课标 新考向
【新课标·综合与实践】问题情境:数学活动课上,老师要求同学们以矩形
为背景探索几何图形运动变化中的数学结论.如图(1),在矩形 中,
为对角线的中点,连接.点在边上,且,线段 的延
长线交于点 .
猜想证明:
(1)“笃学”小组发现 ,请你证明这一结论.
证明:如图(1).
图(1)
四边形 是矩形,
, ,
.
为 的中点,
.
,
,
.
,
.
图(1)
操作探究:
(2)“勤思”小组将图(1)中的绕点顺时针旋转(设点, 的对应
点分别为,, ),在认真分析旋转到不同位置时的情
形后,提出如下问题,请你解答:
图(1)
①如图(2),当点落在的延长线上时,连接,判断四边形 的
形状,并说明理由;
图(2)
[答案] 四边形 为菱形.
理由如下:
如图(2),由旋转得,, .
图(2)
四边形 为矩形,
,
,
, ,
.
.
,
,
,
.
由(1)得 ,
,
四边形 是菱形.
图(2)
②若,,当线段所在直线与 所在直线垂直时,直接写
出, 两点间的距离.
[答案] ,两点间的距离为或 .
解法提示:在中, ,, ,
,, .
为的中点, .
图(3)
当将绕点顺时针旋转 时,点的对应点
落在线段上,此时,如图(3),过点
作,交的延长线于点,连接 .
由旋转可知,, .
又 ,
,
,,, ,
, .
图(4)
当顺时针旋转 时,点的对应点落在线段 的
延长线上,此时,如图(4),过点作 ,
垂足为点,连接 .
由旋转可知,, .
又 , ,
,,, ,
, .
综上,,两点间的距离为或 .
同课章节目录
