2.3.1平面向量的基本定理

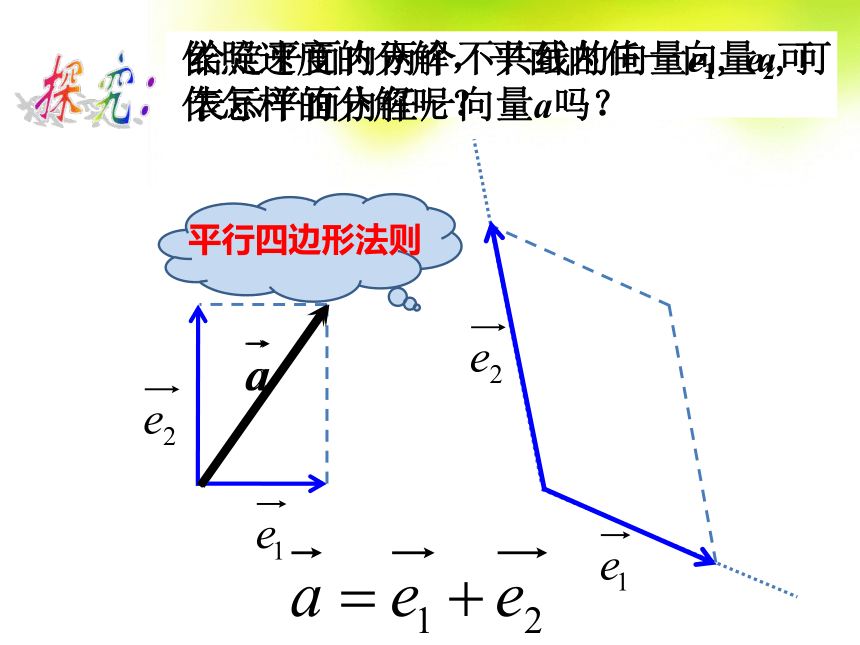
课件23张PPT。2.3.1 平面向量的基本定理已知非零向量 ，那么在同一平面内的任意向量 是否可以由向量 的线性来表示呢？两个向量？
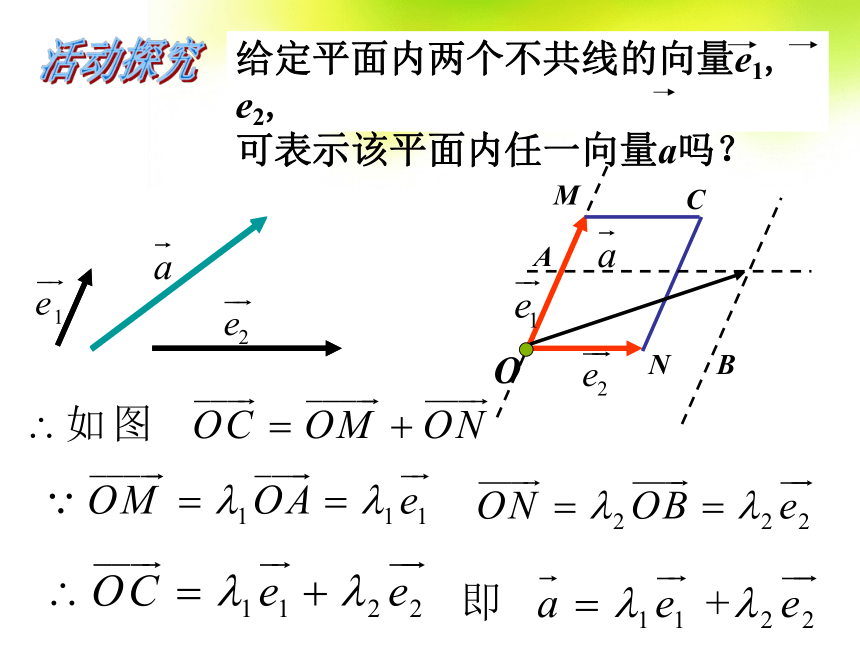
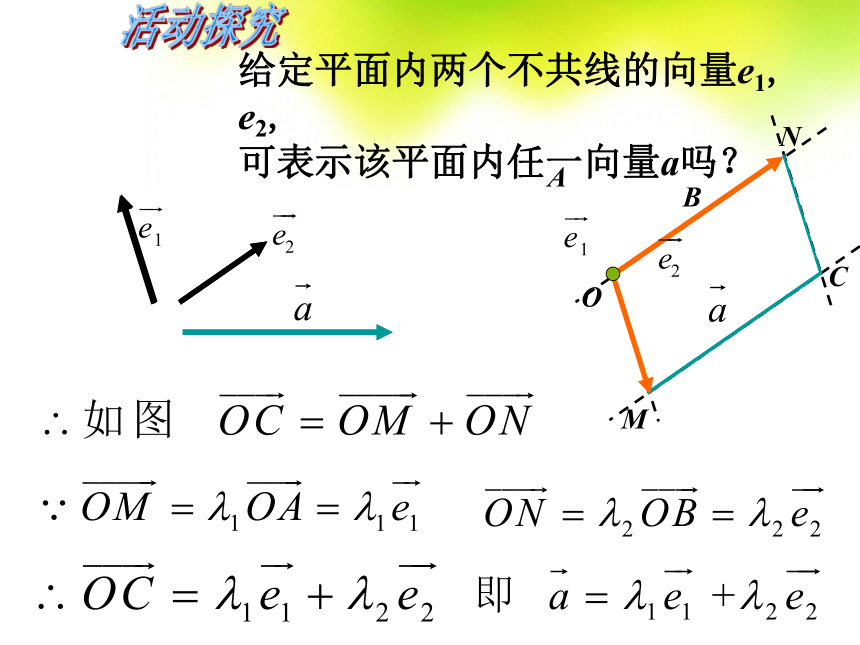
给定平面内两个不共线的向量e1, e2,可
表示平面内任一向量a吗？依照速度的分解，平面内任一向量a可作怎样的分解呢？OCABMN活动探究想一想：OCABMN活动探究给定平面内两个不共线的向量e1, e2,
可表示该平面内任一向量a吗？平面向量基本定理：问题一： 基底不共线也不唯一，任意两个不共线的向量均可作基底． 给定基底后，任意一个向量的表示是唯一的．问题二：平面向量基本定理 如果 是同一平面内的两个不共线向量,那么对于这个平面内的任意一向量 有且只有一对实数 使 ·······对定理的理解：
(1)平面内的任一向量都可以沿两个不共 线的方向分解成两个向量的和的形式；
(2)分解是唯一的。一维直线二维平面6．已知e1，e2是不共线向量，若e1＋2e2与me1＋ne2共线，2全优51页能力提高2．设a，b是平面内的一组基底，则下列四组向量能作为平面向量的基底的是(　　)A．a－b，b－aC．2b－3a,6a－4b D．a＋b，a－bD全优91页限时规范训练3．在梯形ABCD中，AD∥BC，O为梯形所在平面内任意一点，E，F分别为AB，CD的中点，则(　　)C全优50页基础夯实4．(2014年泸州一模)在△ABC中，已知D是AB边上一点，则λ＝(　　)A【解析】如图所示．全优50页基础夯实2．在平行四边形ABCD中，M，N分别是CD，BC的中点，设试以a，b为基底表示向量【解析】根据向量加法的三角形法则有全优50页变式训练4．如图，点D，E，F分别是△ABC的三边BC，CA，AB上的点且0【解析】由题意，得＝0.全优91页限时规范训练3．如图，D，E，F分别是△ABC的边AB，BC，CA的中点．1【解析】∵点D，E，F分别为△ABC的边AB，BC，CA的中点，全优91页限时规范训练O一个重要结论结论：向量的夹角与垂直:夹角的范围：注意:两向量必须是同起点的 zxx、k
【例3】 已知|a|＝|b|＝2，〈a，b〉＝80°，求〈a－b，b〉的大小．【解析】如图，并使∠BAC＝80°.由于|a|＝|b|＝2，所以△ABC为等腰三角形，由于〈a，b〉＝80°，即∠BAC＝80°，所以∠ABC＝∠ACB＝50°，平移向量b，使其起点与a－b的起点重合，则∠ACB的补角为a－b与b的夹角．易求得〈a－b，b〉的大小为130°.全优50页典例剖析