安徽模式2024-2025学年八年级上学期期末数学试卷(六)(含解析)
文档属性
| 名称 | 安徽模式2024-2025学年八年级上学期期末数学试卷(六)(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
安徽模式2024-2025学年八年级上学期期末数学试卷(六)
考试时间:100分钟 满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题
1.下列计算,正确的是( )
A. B.
C. D.
2.水滴穿石,水珠不断滴在一块石头上,经过若干年,石头上形成了一个深为0.0000068cm的小洞,则数字0.0000068用科学记数法可表示为( )
A. B. C. D.
3.游戏时,3名同学分别站在三个顶点的位置上、要求在他们中间放一个凳子,谁先坐到凳子上谁获胜,为使游戏公平,则凳子应放置的最适当的位置是在的( )
A.三边垂直平分线的交点 B.三条角平分线的交点
C.三边中线的交点 D.三边上高的交点
4.如图,,点在上,若,则的长为( )
A.3 B.4 C.5 D.6
5.铜仁市少数民族众多,如图是带有苗族元素的刺绣花,它是一个轴对称图形,将其放置在平面直角坐标系中,如果图中点A的坐标为,其关于y轴对称的点B的坐标为,则的值为( )
A. B. C.5 D.1
6.如图,B点在处的南偏西方向,处在处的南偏东方向,处在北偏东方向,则( )
A. B. C. D.
7.在多项式上添加一个单项式,使得到的多项式可以用完全平方公式进行因式分解,则添加的单项式不可以是( )
A. B. C. D.
8.《九章算术》之“均输篇”中记载了中国古代的“运粟之法”:今有一批公粮,需运往距出发地的储粮站,若运输这批公粮比原计划每日多行,则提前日到达储粮站.设运输这批公粮原计划每日行,则根据题意可列出的方程是( )
A. B. C. D.
9.如图,正和正中,共线,且,连接和相交于点F,连接,以下结论中不正确的是( )
A. B.平分 C. D.
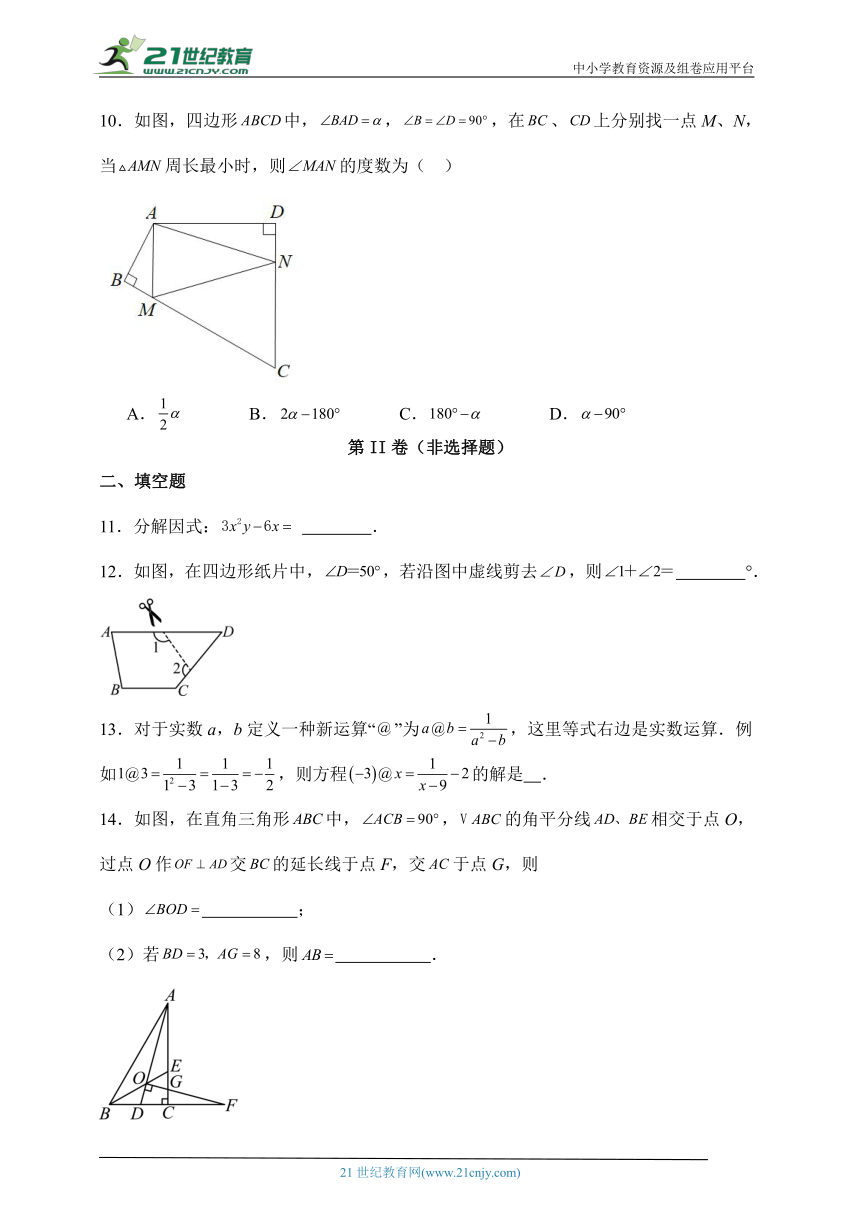
10.如图,四边形中,,,在、上分别找一点M、N,当周长最小时,则的度数为( )
A. B. C. D.
第II卷(非选择题)
二、填空题
11.分解因式: .
12.如图,在四边形纸片中,,若沿图中虚线剪去,则 °.
13.对于实数a,b定义一种新运算“”为,这里等式右边是实数运算.例如,则方程的解是 .
14.如图,在直角三角形中,,的角平分线相交于点O,过点O作交的延长线于点F,交于点G,则
(1) ;
(2)若,则 .
三、解答题
15.(1)计算:;(2)计算:;
(3)分解因式:;(4)分解因式:
16.先化简,再求值:,其中.
17.如图,与在平面直角坐标系中,且的顶点坐标为、、.
(1)画出将向左平移2个单位长度,再向上平移1个单位长度后,关于y轴对称的图形;
(2)连结、C、,所得到的图形______轴对称图形(填是或者不是);若是,画出它的对称轴;
(3)的面积为______.
18.如图,在中,D为BC边上的中点,AE平分交BC于E,交AC于F,,,求CF的长.
19.皮薄汁甜,好吃不上火的爱媛果冻橙近年来备受人们欢迎,某爱媛果冻橙基地11月15日开始采摘发售.采摘发售第一周,大果累计卖了20000元,中果卖了14400元,已知大果每箱单价比中果每箱多,且销量比中果多20箱.
(1)求每箱大果、中果的售价分别是多少元?
(2)由于供不应求,该批发商开始调整价格,第二周每箱大果价格在第一周基础上上涨了,销量减少了20箱,同时每箱中果比第一周多元,销量增加了,最终销售总额比第一周多了7000元,求的值.
20.如图,四边形,、分别平分四边形的外角和,若,.
(1)如图1,若,求的度数;
(2)如图2,若,判断,的位置关系,并说明理由.
21.当光线经过镜面反射时,入射光线、反射光线与镜面所夹的角对应相等.你可用这一结论解答下列问题.
(1)在图(1)中潜望镜的两面镜子AB、CD是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,则进入潜望镜的光线EF和离开潜望镜的光线GH是平行的,请说明理由;
(2)如图(2),改变两平面镜AB、CD之间的位置,若镜子AB与BC的夹角∠ABC=α,经过两次反射后,∠1=∠2,∠3=∠4,仍可以使入射光线EF与反射光线GH平行但方向相反.求α的度数.
(3)拓展应用:如图(3),若镜子AB与BC的夹角α=110°,镜子CD与BC的夹角∠BCD=(90°<<180°),入射光线EF与镜面AB的夹角∠1=30°,已知入射光线EF从镜面AB开始反射,经过n(n为正整数,且n≤3)次反射,当第n次反射光线与入射光线EF平行时,求的度数.
22.定义:若分式与分式的差等于它们的积,即,则称分式是分式的“可存异分式”.如与,因为,,所以是的“可存异分式”.
(1)填空:分式__________分式的“可存异分式”(填“是”或“不是”);
分式的“可存异分式”是__________;
(2)已知分式是分式的“可存异分式”.
求分式的表达式;
求整数为何值时,分式的值是正整数,并写出分式的值.
23.【课例改编】
数学课上,张老师根据数学课本习题改编了一个题目:如图,是的高,,若,求的长.
小明同学的想法是利用构造全等三角形来解决:将沿折叠,如图1,则点刚好落在边上的点处.……
(1)结合小明同学的想法,请直接写出:_____.
【改编拓展】
张老师继续启发同学们改编此题,得到下列试题,请同学们解答:
(2)如图2,为的外角的平分线,交的延长线于点,则线段有什么数量关系?请写出你的猜想并证明.
【模型应用】
根据上面探究构造全等模型的规律,请解答:
(3)如图3,在四边形中,平分,求的长.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A C D C D A C B
1.C
【分析】本题主要考查了幂的运算、合并同类项法则及完全平方公式,熟练掌握其法则是解题的关键.
【详解】解:A、,故此选项错误;
B、,故此选项错误;
C、,故此选项正确;
D、,故此选项错误.
故选:C.
2.D
【详解】试题分析:0.0000068表示成6.8×10-6.
故选D.
考点:科学记数法—表示较小的数.
3.A
【分析】本题主要考查了线段垂直平分线的性质的应用;利用所学的数学知识解决实际问题是一种能力,要注意培养.想到要使凳子到三个人的距离相等是正确解答本题的关键.为使游戏公平,要使凳子到三个人的距离相等,于是利用线段垂直平分线上的点到线段两端的距离相等可知,要放在三边中垂线的交点上.
【详解】解:三角形的三条垂直平分线的交点到三角形各顶点的距离相等,
凳子应放在的三条垂直平分线的交点最适当.
故选:A.
4.C
【分析】本题考查全等三角形的性质,根据,得到,,进而利用求出的长即可.掌握全等三角形的对应边相等,是解题的关键.
【详解】解:∵,
∴,,
∵点在上,
∴;
故选C.
5.D
【分析】本题考查了关于y轴对称的点的坐标特征.关于y轴对称的点横坐标互为相反数,纵坐标相同,据此即可解答.
【详解】解:∵点的坐标为,其关于轴对称的点的坐标为,
∴,,
∴.
故选:D.
6.C
【分析】本题主要考查了方向角的定义,以及三角形的内角和定理.根据方向角的定义,即可求得,,的度数,然后根据三角形内角和定理即可求解.
【详解】解:如图,
,是正南正北方向,
∴,
,
,
,
,
又,
,
.
故选:C.
7.D
【分析】本题主要考查完全平方公式的运用,根据完全平方和(差)公式的性质即可求解.
【详解】解:A选项,,可以构成完全平方和公式,不符合题意;
B选项,,可以构成完全平方差公式,不符合题意;
C选项,,可以构成完全平方和公式,不符合题意;
D选项,,不可以构成完全平方公式,符合题意.
故选:D.
8.A
【分析】设运输这批公粮原计划每日行,根据运输这批公粮比原计划每日多行,则提前日到达储粮站,列出分式方程,即可求解.
【详解】设运输这批公粮原计划每日行,根据题意得,
,
故选:A.
【点睛】本题考查了列分式方程,根据题意列出方程是解题的关键.
9.C
【分析】首先利用SAS证明,,得,即可判断选项A;然后由,得,再利用三角形外角的性质即可判断选项D;过点C作于G,于H,根据全等三角形对应边上的高相等可知,即可判断选项B;由,根据三角形的面积可得,即可判断选项C.
【详解】∵正和正,
∴,
∵B、C、D共线,
∴,
∴,,
∴,
∵是的外角,
∴,
在和中,
,
∴,
∴,故A选项正确,不符合题意;
∵,
∴,
∵是的外角,
∴,故D选项正确,不符合题意;
过点C作于G,于H,
∵,
∴,
∴CF平分,故B选项正确,不符合题意;
过点C作于G,于H,过点F作于M,
∵,
∵,
∴,
∵,
∴,
∵,
∴,
∵,
当时,,
∴,故C选项不正确,符合题意.
故选C.
【点睛】本题考查了等边三角形的性质、全等三角形的判定和性质、角平分线的判定和性质和三角形的面积,解决本题的关键是需要有较强的识图能力.
10.B
【分析】根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′M+∠A″=∠HAA′,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″)即可得出答案.
【详解】解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,
∵∠DAB= ,
∴∠HAA′=,
∴∠AA′M+∠A″=∠HAA′=,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=,
.
故选:B.
【点睛】本题主要考查轴对称-最段路线问题,熟练掌握平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M,N的位置是解题关键.
11.
【分析】本题主要考查了因式分解,解题的关键是掌握因式分解的方法.利用提公因式法即可求解.
【详解】解:
故答案为:.
12.
【分析】根据三角形的内外角之间的关系可求解.
【详解】解:三角形的内角和等于,,
,.
,
.
故答案为:.
【点睛】本题考查了多边形的内角与外角,解题的关键是明确三角形的内外角之间的关系和三角形的内角和等于的知识点.
13.x=10
【分析】根据新定义的运算求出,即得出关于x的分式方程,再解方程即可.
【详解】解:,
∴,
等式两边同时乘,得:,
解得:.
经检验是原分式方程的解.
∴方程的解是.
故答案为:x=10.
【点睛】本题考查新定义下的实数运算,解分式方程.理解题意,掌握新定义的运算法则是解题关键.
14. 11
【分析】本题考查了全等三角形的判定和性质,直角三角形的性质,角平分线的性质等知识,
(1)由角平分线的性质可得,,由三角形内角和定理可求,
(2)由“”可证,可得,由“”可证,可得,由全等三角形的性质可得.
【详解】解:(1)∵的角平分线相交于点O,
∴,,,
∴,
∴,
故答案为:
(2)∵,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∵,
∴,
又∵,
在和中,
,
∴,
∴,
∵,
∴,
∴.
故答案为:11.
15.(1);(2);(3);(4)
【分析】本题考查积的乘方,整式的除法,因式分解.
(1)根据积的乘方计算,再合并同类项即可;
(2)根据整式的除法法则计算;
(3)先提公因式后,再用平方差公式分解因式;
(4)先提公因式后,再用完全平方公式分解因式.
【详解】(1);
(2);
(3);
(4).
16.,
【分析】本题主要考查了分式的化简求值,先去小括号得到,再把除数的分子分解因式,进而把除法变成乘法,然后约分化简,最后利用整体代入法代值计算即可.
【详解】解;
,
∵,
∴原式.
17.(1)见详解;
(2)是,图见详解;
(3)1.
【分析】本题考查的是作图-旋转变换,熟知图形旋转不变性的性质是解答此题的关键.
(1)根据图形平移及轴对称的性质画出即可;
(2)画出计算边长,画出对称轴即可;
(3)根据图形计算即可得出结论.
【详解】(1)解∶ 的三个顶点的坐标分别为、、,
将向左平移2个单位长度,再向上平移1个单位长度后,关于y轴对称的点的坐标分别为,
在平面直角坐标系中依次描出这些点,顺次连接可得,如下图所示:
(2),,
,
所以所得图形是等腰三角形,是轴对称图形,
对称轴如图所示.
(3)如图,
.
18.
【分析】延长DF交BA延长线与点G,延长FD到H使得,连接BH,由平分,,首先证明,然后根据可得,最后由可列出方程求出CF的值.
【详解】解:延长DF交BA延长线与点G,延长FD到H使得,连接BH.
平分,,
,
,
又,,易得,
,,
则,
设,则,,
解得,,.
【点睛】本题考查平行线的性质、角平分线的性质以及三角形全等的判定和性质,根据题意构造出全等三角形是解题关键.
19.(1)每箱大果的售价100元、每箱中果的售价分80元
(2)10
【分析】本题考查一元一次方程的应用,解答本题的关键是明确题意,列出相应的方程.
(1)设中果的售价为元,则大果的售价;再根据“大果累计卖了20000元,中果卖了14400元,已知大果每箱单价比中果每箱多,且销量比中果多20箱”列方程即可;
(2)根据题意和(1)中的结果,可以列出相应的方程,从而可以求得的值.
【详解】(1)解:设每箱中果的售价为元,则每箱大果的售价
由题意可得:,
解得,
经检验是原方程的解,
∴大果的售价元
答:每箱大果的售价100元、每箱中果的售价分80元;
(2)由题意可得,
,
解得,
即的值是10.
答:的值是10.
20.(1);
(2),理由见解析
【分析】(1)利用四边形的内角和和角平分线的定义推导即可;
(2)利用角平分线的定义以及平行线的判定与性质即可解答.
【详解】(1)解:∵四边形的内角和为,
∴,
∵和是四边形的外角,
∴,,
∴
,
β
,
∵、分别平分和,
∴;
(2)解:.理由:
如图,过点作,
∴,
∴,
由()知,
∵,
∴,
又∵、分别平分和,
∴,
∴,
又∵,
∴,
∴,
又,
∴.
【点睛】此题主要考查了平行线的性质及其判定、平角的定义,四边形的内角和,角平分线的定义,用整体代换的思想是解本题的关键,整体思想是初中阶段的一种重要思想,要多加强训练.
21.(1)见解析
(2)90°
(3)120°或160°
【分析】(1)根据题意可得,所以∠2=∠3,由已知∠1=∠2,∠3=∠4.可得,进而可以说明.
(2)由平行线的性质得出∠FEG+∠EGH=180°,根据平角的定义得出∠1+∠2+∠FEG+∠3+∠4+∠EGH=180°+180°=360°,进而得到∠2+∠3=90°,再根据三角形的内角和即可得解.
(3)分两种情况画图讨论:①当n=3时,根据入射光线、反射光线与镜面所夹的角对应相等,及内角和,可得.②当n=2时,如果在BC边反射后与EF平行,则,与题意不符;则只能在CD边反射后与EF平行,根据三角形外角定义,可得,由,且由(2)的结论可得, .
【详解】(1)解:(1)如图(1),
∵,
∴∠2=∠3,
∵,
∴,
∴,
即:,
∴;
(2)(2)如图(2),
∵,
∴∠FEG+∠EGH=180°,
∴∠1+∠2+∠FEG+∠3+∠4+∠EGH=180°+180°=360°,
∴∠1+∠2+∠3+∠4=180°,
∵∠1=∠2,∠3=∠4,
∴2(∠2+∠3)=180°,
∴∠2+∠3=90°,
∵∠ABC+∠2+∠3=180°,
∴∠ABC=180°﹣∠2﹣∠3=180°﹣90°=90°,
即α的度数为90°.
(3)(3)(ⅰ)当n=3时,如图(3)所示:
∵∠BEG=∠1=30°,α=110°,
∴∠BGE=∠CGH=180°﹣110°- 30°=40°,
∴∠FEG=180°﹣2∠1=120°,
∠EGH=180°﹣2∠BGE=100°,
由,可得∠FEG+∠EGH+∠GHK=360°,
∴∠GHK=360°﹣120°﹣100°=140°,
则∠GHC=20°,
∴=180°﹣40°﹣20°=120°.
(ⅱ)当n=2时,如果在BC边反射后与EF平行,则α=90°,
与题意不符;
则只能在CD边反射后与EF平行,
如图(4)所示:
+∠GCB=180°,,
,
由,且由(2)的结论可得:∠G=90°,
又,
∴=90°+70°=160°.
综上所述:的度数为:120°或160°.
【点睛】本题考查了平行线的性质与判定、三角形内角和,解决本题的关键是掌握平行线的性质,注意分类讨论思想的应用.
22.(1)不是;;
(2);,或.
【分析】()根据“可存异分式”的定义进行判断即可;
根据“可存异分式”的定义进行解答即可求解;
()根据“可存异分式”的定义进行解答即可求解;
根据整除的定义进行求解即可;
本题考查了分式加减运算、乘法运算,解分式方程,代数式求值,掌握分式的运算法则是解题的关键.
【详解】(1)解:,
分式不是分式的“可存异分式”,
故答案为:不是;
依题意得,,
∴,
解得,
即分式的“可存异分式”是,
故答案为:;
(2)解:依题意,
∴,
解得;
,
当整数或时,分式的值分别是1,,或,
又分式的值是正数,
整数或,分式的值分别是,或.
23.(1)见解析;(2),见解析;(3)
【分析】(1)根据题意画出图形,由折叠的性质可得:,,,由可得,再由三角形外角的定义及性质可得,推出,进而得到,最后进行计算即可得到答案;
(2)在上截取,连接,证明得到,,证明,再由得到,再根据三角形外角的定义及性质得出,进而得到,即可得证;
(3)在上截取,连接,证明,得到,,从而得到,进而,再由即可得证,结合可得,从而推出是等边三角形,得出,最后由即可得到答案.
【详解】(1)解:如图,将沿折叠,则点C刚好落在边上的点E处,
由折叠的性质可得:,,,
,
,
,
,
,
;
(2)解:,
证明:如图,在上截取,连接,
,
平分,
,
在和中,
,
,
,,
,,
,
,
,
,
,
,
,
;
(3)解:如图,在上截取,连接,
平分,
,
在和中,
,
,
,,
,
,
,
,
,
,
,
,
,
为等边三角形,
,
.
【点睛】本题主要考查了角平分线的定义、三角形全等的判定与性质、三角形外角的定义及性质、等边三角形的判定与性质、等腰三角形的判定与性质、折叠的性质等知识点,熟练掌握以上知识点,添加适当的辅助线是解此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
安徽模式2024-2025学年八年级上学期期末数学试卷(六)
考试时间:100分钟 满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题
1.下列计算,正确的是( )
A. B.
C. D.
2.水滴穿石,水珠不断滴在一块石头上,经过若干年,石头上形成了一个深为0.0000068cm的小洞,则数字0.0000068用科学记数法可表示为( )
A. B. C. D.
3.游戏时,3名同学分别站在三个顶点的位置上、要求在他们中间放一个凳子,谁先坐到凳子上谁获胜,为使游戏公平,则凳子应放置的最适当的位置是在的( )
A.三边垂直平分线的交点 B.三条角平分线的交点
C.三边中线的交点 D.三边上高的交点
4.如图,,点在上,若,则的长为( )
A.3 B.4 C.5 D.6
5.铜仁市少数民族众多,如图是带有苗族元素的刺绣花,它是一个轴对称图形,将其放置在平面直角坐标系中,如果图中点A的坐标为,其关于y轴对称的点B的坐标为,则的值为( )
A. B. C.5 D.1
6.如图,B点在处的南偏西方向,处在处的南偏东方向,处在北偏东方向,则( )
A. B. C. D.
7.在多项式上添加一个单项式,使得到的多项式可以用完全平方公式进行因式分解,则添加的单项式不可以是( )
A. B. C. D.
8.《九章算术》之“均输篇”中记载了中国古代的“运粟之法”:今有一批公粮,需运往距出发地的储粮站,若运输这批公粮比原计划每日多行,则提前日到达储粮站.设运输这批公粮原计划每日行,则根据题意可列出的方程是( )
A. B. C. D.
9.如图,正和正中,共线,且,连接和相交于点F,连接,以下结论中不正确的是( )
A. B.平分 C. D.
10.如图,四边形中,,,在、上分别找一点M、N,当周长最小时,则的度数为( )
A. B. C. D.
第II卷(非选择题)
二、填空题
11.分解因式: .
12.如图,在四边形纸片中,,若沿图中虚线剪去,则 °.
13.对于实数a,b定义一种新运算“”为,这里等式右边是实数运算.例如,则方程的解是 .
14.如图,在直角三角形中,,的角平分线相交于点O,过点O作交的延长线于点F,交于点G,则
(1) ;
(2)若,则 .
三、解答题
15.(1)计算:;(2)计算:;
(3)分解因式:;(4)分解因式:
16.先化简,再求值:,其中.
17.如图,与在平面直角坐标系中,且的顶点坐标为、、.
(1)画出将向左平移2个单位长度,再向上平移1个单位长度后,关于y轴对称的图形;
(2)连结、C、,所得到的图形______轴对称图形(填是或者不是);若是,画出它的对称轴;
(3)的面积为______.
18.如图,在中,D为BC边上的中点,AE平分交BC于E,交AC于F,,,求CF的长.
19.皮薄汁甜,好吃不上火的爱媛果冻橙近年来备受人们欢迎,某爱媛果冻橙基地11月15日开始采摘发售.采摘发售第一周,大果累计卖了20000元,中果卖了14400元,已知大果每箱单价比中果每箱多,且销量比中果多20箱.
(1)求每箱大果、中果的售价分别是多少元?
(2)由于供不应求,该批发商开始调整价格,第二周每箱大果价格在第一周基础上上涨了,销量减少了20箱,同时每箱中果比第一周多元,销量增加了,最终销售总额比第一周多了7000元,求的值.
20.如图,四边形,、分别平分四边形的外角和,若,.
(1)如图1,若,求的度数;
(2)如图2,若,判断,的位置关系,并说明理由.
21.当光线经过镜面反射时,入射光线、反射光线与镜面所夹的角对应相等.你可用这一结论解答下列问题.
(1)在图(1)中潜望镜的两面镜子AB、CD是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,则进入潜望镜的光线EF和离开潜望镜的光线GH是平行的,请说明理由;
(2)如图(2),改变两平面镜AB、CD之间的位置,若镜子AB与BC的夹角∠ABC=α,经过两次反射后,∠1=∠2,∠3=∠4,仍可以使入射光线EF与反射光线GH平行但方向相反.求α的度数.
(3)拓展应用:如图(3),若镜子AB与BC的夹角α=110°,镜子CD与BC的夹角∠BCD=(90°<<180°),入射光线EF与镜面AB的夹角∠1=30°,已知入射光线EF从镜面AB开始反射,经过n(n为正整数,且n≤3)次反射,当第n次反射光线与入射光线EF平行时,求的度数.
22.定义:若分式与分式的差等于它们的积,即,则称分式是分式的“可存异分式”.如与,因为,,所以是的“可存异分式”.
(1)填空:分式__________分式的“可存异分式”(填“是”或“不是”);
分式的“可存异分式”是__________;
(2)已知分式是分式的“可存异分式”.
求分式的表达式;
求整数为何值时,分式的值是正整数,并写出分式的值.
23.【课例改编】
数学课上,张老师根据数学课本习题改编了一个题目:如图,是的高,,若,求的长.
小明同学的想法是利用构造全等三角形来解决:将沿折叠,如图1,则点刚好落在边上的点处.……
(1)结合小明同学的想法,请直接写出:_____.
【改编拓展】
张老师继续启发同学们改编此题,得到下列试题,请同学们解答:
(2)如图2,为的外角的平分线,交的延长线于点,则线段有什么数量关系?请写出你的猜想并证明.
【模型应用】
根据上面探究构造全等模型的规律,请解答:
(3)如图3,在四边形中,平分,求的长.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C D A C D C D A C B
1.C
【分析】本题主要考查了幂的运算、合并同类项法则及完全平方公式,熟练掌握其法则是解题的关键.
【详解】解:A、,故此选项错误;
B、,故此选项错误;
C、,故此选项正确;
D、,故此选项错误.
故选:C.
2.D
【详解】试题分析:0.0000068表示成6.8×10-6.
故选D.
考点:科学记数法—表示较小的数.
3.A
【分析】本题主要考查了线段垂直平分线的性质的应用;利用所学的数学知识解决实际问题是一种能力,要注意培养.想到要使凳子到三个人的距离相等是正确解答本题的关键.为使游戏公平,要使凳子到三个人的距离相等,于是利用线段垂直平分线上的点到线段两端的距离相等可知,要放在三边中垂线的交点上.
【详解】解:三角形的三条垂直平分线的交点到三角形各顶点的距离相等,
凳子应放在的三条垂直平分线的交点最适当.
故选:A.
4.C
【分析】本题考查全等三角形的性质,根据,得到,,进而利用求出的长即可.掌握全等三角形的对应边相等,是解题的关键.
【详解】解:∵,
∴,,
∵点在上,
∴;
故选C.
5.D
【分析】本题考查了关于y轴对称的点的坐标特征.关于y轴对称的点横坐标互为相反数,纵坐标相同,据此即可解答.
【详解】解:∵点的坐标为,其关于轴对称的点的坐标为,
∴,,
∴.
故选:D.
6.C
【分析】本题主要考查了方向角的定义,以及三角形的内角和定理.根据方向角的定义,即可求得,,的度数,然后根据三角形内角和定理即可求解.
【详解】解:如图,
,是正南正北方向,
∴,
,
,
,
,
又,
,
.
故选:C.
7.D
【分析】本题主要考查完全平方公式的运用,根据完全平方和(差)公式的性质即可求解.
【详解】解:A选项,,可以构成完全平方和公式,不符合题意;
B选项,,可以构成完全平方差公式,不符合题意;
C选项,,可以构成完全平方和公式,不符合题意;
D选项,,不可以构成完全平方公式,符合题意.
故选:D.
8.A
【分析】设运输这批公粮原计划每日行,根据运输这批公粮比原计划每日多行,则提前日到达储粮站,列出分式方程,即可求解.
【详解】设运输这批公粮原计划每日行,根据题意得,
,
故选:A.
【点睛】本题考查了列分式方程,根据题意列出方程是解题的关键.
9.C
【分析】首先利用SAS证明,,得,即可判断选项A;然后由,得,再利用三角形外角的性质即可判断选项D;过点C作于G,于H,根据全等三角形对应边上的高相等可知,即可判断选项B;由,根据三角形的面积可得,即可判断选项C.
【详解】∵正和正,
∴,
∵B、C、D共线,
∴,
∴,,
∴,
∵是的外角,
∴,
在和中,
,
∴,
∴,故A选项正确,不符合题意;
∵,
∴,
∵是的外角,
∴,故D选项正确,不符合题意;
过点C作于G,于H,
∵,
∴,
∴CF平分,故B选项正确,不符合题意;
过点C作于G,于H,过点F作于M,
∵,
∵,
∴,
∵,
∴,
∵,
∴,
∵,
当时,,
∴,故C选项不正确,符合题意.
故选C.
【点睛】本题考查了等边三角形的性质、全等三角形的判定和性质、角平分线的判定和性质和三角形的面积,解决本题的关键是需要有较强的识图能力.
10.B
【分析】根据要使△AMN的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A关于BC和CD的对称点A′,A″,即可得出∠AA′M+∠A″=∠HAA′,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″)即可得出答案.
【详解】解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于M,交CD于N,则A′A″即为△AMN的周长最小值.作DA延长线AH,
∵∠DAB= ,
∴∠HAA′=,
∴∠AA′M+∠A″=∠HAA′=,
∵∠MA′A=∠MAA′,∠NAD=∠A″,
且∠MA′A+∠MAA′=∠AMN,∠NAD+∠A″=∠ANM,
∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=,
.
故选:B.
【点睛】本题主要考查轴对称-最段路线问题,熟练掌握平面内最短路线问题求法以及三角形的外角的性质和垂直平分线的性质等知识,根据已知得出M,N的位置是解题关键.
11.
【分析】本题主要考查了因式分解,解题的关键是掌握因式分解的方法.利用提公因式法即可求解.
【详解】解:
故答案为:.
12.
【分析】根据三角形的内外角之间的关系可求解.
【详解】解:三角形的内角和等于,,
,.
,
.
故答案为:.
【点睛】本题考查了多边形的内角与外角,解题的关键是明确三角形的内外角之间的关系和三角形的内角和等于的知识点.
13.x=10
【分析】根据新定义的运算求出,即得出关于x的分式方程,再解方程即可.
【详解】解:,
∴,
等式两边同时乘,得:,
解得:.
经检验是原分式方程的解.
∴方程的解是.
故答案为:x=10.
【点睛】本题考查新定义下的实数运算,解分式方程.理解题意,掌握新定义的运算法则是解题关键.
14. 11
【分析】本题考查了全等三角形的判定和性质,直角三角形的性质,角平分线的性质等知识,
(1)由角平分线的性质可得,,由三角形内角和定理可求,
(2)由“”可证,可得,由“”可证,可得,由全等三角形的性质可得.
【详解】解:(1)∵的角平分线相交于点O,
∴,,,
∴,
∴,
故答案为:
(2)∵,
∴,
∴,
∴,
在和中,
,
∴,
∴,
∵,
∴,
又∵,
在和中,
,
∴,
∴,
∵,
∴,
∴.
故答案为:11.
15.(1);(2);(3);(4)
【分析】本题考查积的乘方,整式的除法,因式分解.
(1)根据积的乘方计算,再合并同类项即可;
(2)根据整式的除法法则计算;
(3)先提公因式后,再用平方差公式分解因式;
(4)先提公因式后,再用完全平方公式分解因式.
【详解】(1);
(2);
(3);
(4).
16.,
【分析】本题主要考查了分式的化简求值,先去小括号得到,再把除数的分子分解因式,进而把除法变成乘法,然后约分化简,最后利用整体代入法代值计算即可.
【详解】解;
,
∵,
∴原式.
17.(1)见详解;
(2)是,图见详解;
(3)1.
【分析】本题考查的是作图-旋转变换,熟知图形旋转不变性的性质是解答此题的关键.
(1)根据图形平移及轴对称的性质画出即可;
(2)画出计算边长,画出对称轴即可;
(3)根据图形计算即可得出结论.
【详解】(1)解∶ 的三个顶点的坐标分别为、、,
将向左平移2个单位长度,再向上平移1个单位长度后,关于y轴对称的点的坐标分别为,
在平面直角坐标系中依次描出这些点,顺次连接可得,如下图所示:
(2),,
,
所以所得图形是等腰三角形,是轴对称图形,
对称轴如图所示.
(3)如图,
.
18.
【分析】延长DF交BA延长线与点G,延长FD到H使得,连接BH,由平分,,首先证明,然后根据可得,最后由可列出方程求出CF的值.
【详解】解:延长DF交BA延长线与点G,延长FD到H使得,连接BH.
平分,,
,
,
又,,易得,
,,
则,
设,则,,
解得,,.
【点睛】本题考查平行线的性质、角平分线的性质以及三角形全等的判定和性质,根据题意构造出全等三角形是解题关键.
19.(1)每箱大果的售价100元、每箱中果的售价分80元
(2)10
【分析】本题考查一元一次方程的应用,解答本题的关键是明确题意,列出相应的方程.
(1)设中果的售价为元,则大果的售价;再根据“大果累计卖了20000元,中果卖了14400元,已知大果每箱单价比中果每箱多,且销量比中果多20箱”列方程即可;
(2)根据题意和(1)中的结果,可以列出相应的方程,从而可以求得的值.
【详解】(1)解:设每箱中果的售价为元,则每箱大果的售价
由题意可得:,
解得,
经检验是原方程的解,
∴大果的售价元
答:每箱大果的售价100元、每箱中果的售价分80元;
(2)由题意可得,
,
解得,
即的值是10.
答:的值是10.
20.(1);
(2),理由见解析
【分析】(1)利用四边形的内角和和角平分线的定义推导即可;
(2)利用角平分线的定义以及平行线的判定与性质即可解答.
【详解】(1)解:∵四边形的内角和为,
∴,
∵和是四边形的外角,
∴,,
∴
,
β
,
∵、分别平分和,
∴;
(2)解:.理由:
如图,过点作,
∴,
∴,
由()知,
∵,
∴,
又∵、分别平分和,
∴,
∴,
又∵,
∴,
∴,
又,
∴.
【点睛】此题主要考查了平行线的性质及其判定、平角的定义,四边形的内角和,角平分线的定义,用整体代换的思想是解本题的关键,整体思想是初中阶段的一种重要思想,要多加强训练.
21.(1)见解析
(2)90°
(3)120°或160°
【分析】(1)根据题意可得,所以∠2=∠3,由已知∠1=∠2,∠3=∠4.可得,进而可以说明.
(2)由平行线的性质得出∠FEG+∠EGH=180°,根据平角的定义得出∠1+∠2+∠FEG+∠3+∠4+∠EGH=180°+180°=360°,进而得到∠2+∠3=90°,再根据三角形的内角和即可得解.
(3)分两种情况画图讨论:①当n=3时,根据入射光线、反射光线与镜面所夹的角对应相等,及内角和,可得.②当n=2时,如果在BC边反射后与EF平行,则,与题意不符;则只能在CD边反射后与EF平行,根据三角形外角定义,可得,由,且由(2)的结论可得, .
【详解】(1)解:(1)如图(1),
∵,
∴∠2=∠3,
∵,
∴,
∴,
即:,
∴;
(2)(2)如图(2),
∵,
∴∠FEG+∠EGH=180°,
∴∠1+∠2+∠FEG+∠3+∠4+∠EGH=180°+180°=360°,
∴∠1+∠2+∠3+∠4=180°,
∵∠1=∠2,∠3=∠4,
∴2(∠2+∠3)=180°,
∴∠2+∠3=90°,
∵∠ABC+∠2+∠3=180°,
∴∠ABC=180°﹣∠2﹣∠3=180°﹣90°=90°,
即α的度数为90°.
(3)(3)(ⅰ)当n=3时,如图(3)所示:
∵∠BEG=∠1=30°,α=110°,
∴∠BGE=∠CGH=180°﹣110°- 30°=40°,
∴∠FEG=180°﹣2∠1=120°,
∠EGH=180°﹣2∠BGE=100°,
由,可得∠FEG+∠EGH+∠GHK=360°,
∴∠GHK=360°﹣120°﹣100°=140°,
则∠GHC=20°,
∴=180°﹣40°﹣20°=120°.
(ⅱ)当n=2时,如果在BC边反射后与EF平行,则α=90°,
与题意不符;
则只能在CD边反射后与EF平行,
如图(4)所示:
+∠GCB=180°,,
,
由,且由(2)的结论可得:∠G=90°,
又,
∴=90°+70°=160°.
综上所述:的度数为:120°或160°.
【点睛】本题考查了平行线的性质与判定、三角形内角和,解决本题的关键是掌握平行线的性质,注意分类讨论思想的应用.
22.(1)不是;;
(2);,或.
【分析】()根据“可存异分式”的定义进行判断即可;
根据“可存异分式”的定义进行解答即可求解;
()根据“可存异分式”的定义进行解答即可求解;
根据整除的定义进行求解即可;
本题考查了分式加减运算、乘法运算,解分式方程,代数式求值,掌握分式的运算法则是解题的关键.
【详解】(1)解:,
分式不是分式的“可存异分式”,
故答案为:不是;
依题意得,,
∴,
解得,
即分式的“可存异分式”是,
故答案为:;
(2)解:依题意,
∴,
解得;
,
当整数或时,分式的值分别是1,,或,
又分式的值是正数,
整数或,分式的值分别是,或.
23.(1)见解析;(2),见解析;(3)
【分析】(1)根据题意画出图形,由折叠的性质可得:,,,由可得,再由三角形外角的定义及性质可得,推出,进而得到,最后进行计算即可得到答案;
(2)在上截取,连接,证明得到,,证明,再由得到,再根据三角形外角的定义及性质得出,进而得到,即可得证;
(3)在上截取,连接,证明,得到,,从而得到,进而,再由即可得证,结合可得,从而推出是等边三角形,得出,最后由即可得到答案.
【详解】(1)解:如图,将沿折叠,则点C刚好落在边上的点E处,
由折叠的性质可得:,,,
,
,
,
,
,
;
(2)解:,
证明:如图,在上截取,连接,
,
平分,
,
在和中,
,
,
,,
,,
,
,
,
,
,
,
,
;
(3)解:如图,在上截取,连接,
平分,
,
在和中,
,
,
,,
,
,
,
,
,
,
,
,
,
为等边三角形,
,
.
【点睛】本题主要考查了角平分线的定义、三角形全等的判定与性质、三角形外角的定义及性质、等边三角形的判定与性质、等腰三角形的判定与性质、折叠的性质等知识点,熟练掌握以上知识点,添加适当的辅助线是解此题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
