安徽模式2024-2025学年八年级上学期期末数学试卷(二)(含解析)
文档属性
| 名称 | 安徽模式2024-2025学年八年级上学期期末数学试卷(二)(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 13:56:52 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
安徽模式2024-2025学年八年级上学期期末数学试卷(二)
考试时间:100分钟 满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题
1.下列长度的三条线段能组成三角形的是( )
A.1,2,3.5 B.4,5,9
C.3,5,7 D.5,15,8
2.芜湖水稻种植历史悠久,素有“江南鱼米之乡”的美誉,也曾是“四大米市”之一,所产芜湖大米杍粒细长,晶莹剔透,蒸煮后清香扑鼻,柔韧可口.已知一粒米的重量约0.000021千克,将数据0.000021用科学记数法表示为( )
A. B. C. D.
3.下列运算正确的是( )
A. B.
C. D.
4.数学中有许多精美的曲线.以下是“笛卡尔叶形线”“阿基米德螺线”“三叶玫瑰线”和“星形线”,其中一定不是轴对称图形的是( )
A. B. C. D.
5.图中的两个三角形全等,则等于( )
A. B. C. D.
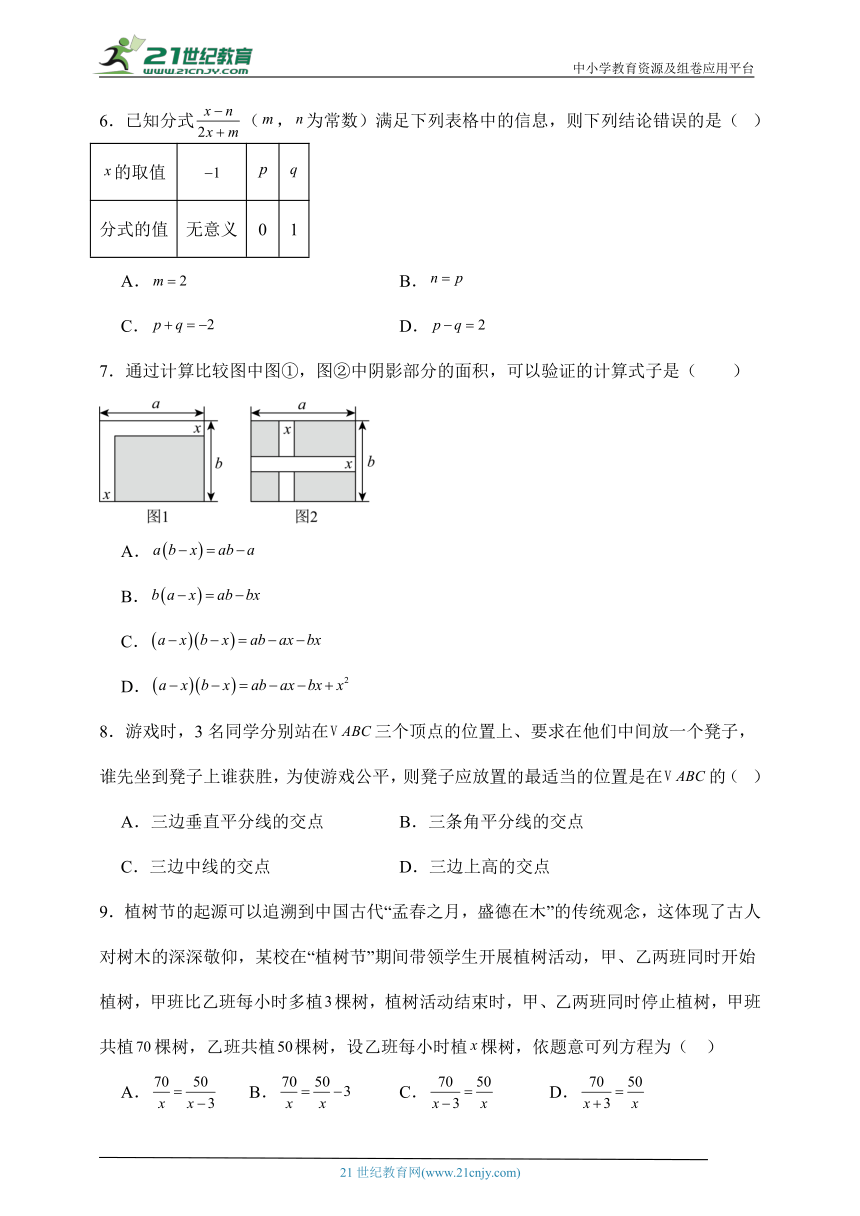
6.已知分式(,为常数)满足下列表格中的信息,则下列结论错误的是( )
的取值
分式的值 无意义 0 1
A. B.
C. D.
7.通过计算比较图中图①,图②中阴影部分的面积,可以验证的计算式子是( )
A.
B.
C.
D.
8.游戏时,3名同学分别站在三个顶点的位置上、要求在他们中间放一个凳子,谁先坐到凳子上谁获胜,为使游戏公平,则凳子应放置的最适当的位置是在的( )
A.三边垂直平分线的交点 B.三条角平分线的交点
C.三边中线的交点 D.三边上高的交点
9.植树节的起源可以追溯到中国古代“孟春之月,盛德在木”的传统观念,这体现了古人对树木的深深敬仰,某校在“植树节”期间带领学生开展植树活动,甲、乙两班同时开始植树,甲班比乙班每小时多植棵树,植树活动结束时,甲、乙两班同时停止植树,甲班共植棵树,乙班共植棵树,设乙班每小时植棵树,依题意可列方程为( )
A. B. C. D.
10.如图,在锐角三角形中,,的面积为18,平分,若、分别是、上的动点,则的最小值必( )
A.5 B.6 C.7 D.8
第II卷(非选择题)
二、填空题
11.点 P( 3,5)关于x 轴的对称点的坐标为 .
12.若,则多项式的值是 .
13.课本上的这幅插图直观验证了多边形的一条性质,它是: .
14.已知分式.
(1)如果,那么的取值范围是 .
(2)若,且,则的值为 .
三、解答题
15.(1)计算:;(2)解方程:
16.如图,在中,,,,、交于点.在不添加字母和辅助线的情况下,请你在图中找出一对全等三角形并证明.
17.如图,的顶点在正方形网格的格点上.
画关于直线的轴对称图形(不写画法);作中边上的中线(请用无刻度的直尺作图,保留作图痕迹)
18.下面是小彬同学进行分式化简的过程,请认真阅读并完成相应任务.
…………………………①
…………………………②
…………………………③
…………………………④
…………………………⑤
【任务一】填空:
①以上化简步骤中,第______步进行的是分式的通分,通分的依据是______;
②第______步开始出现错误.这一步错误的原因是______;
【任务二】③该分式化简后的正确结果为______
【任务三】④请你根据平时的学习经验,就分式化简时还需要注意的事项给其他同学提一条建议.
19.已知:如图,在中,,点在上,点在边的延长线上,与相交于点.若,求证:.
20.小球悬挂处点到地面的距离是4米,小球从静止状态处开始摆动,摆动到最高点时,测得到的距离为3米,距离地面2.3米.
(1)求小球摆动到垂直于位置时到的距离;
(2)求到地面的距离,写出必要的推理过程.
21.如图,“丰收号”小麦的试验田是边长为的正方形去掉一个边长为m的正方形蓄水池后余下的部分,“丰收号”小麦的试验田是边长为的正方形,两块试验田的小麦都收获了.
(1)哪种小麦的单位面积产量高
(2)若高的单位面积产量是低的单位面积产量的倍,求“丰收号”小麦的试验田的边长.
22.我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应展开式中的系数;第四行的四个数1,3,3,1,恰好对应着展开式中的系数等等.
(1)根据上面的规律,写出的展开式.
(2)利用上面的规律计算:
23.数学是一门充满乐趣、奥妙、又极具探索的学科,对一个人的思维也是一种“挑战”几何图形更是变幻无穷,但只要我们借助图形的直观、特殊情形出发,逐步“从特殊到一般”进行探索,思路和方法自然就会显现出来.下面是一道探索几何图形中线段与数量关系的例子:
已知,在等边三角形中,点E在上,点D 在的延长线上, 且
小星的思路是:
(1)【特殊情况,探索结论】如图1,当点E为的中点时,确定线段与的大小关系, 请你直接写出结论: (填“>”, “<”或“=”);
(2)【特例启发,解答题目】如图2,当点E为边上任意一点时,确定线段与 的大小关系, 请你写出结论: (填“>”,“<”或“=”); 理由如下:(请你将理由补充完整)
证明:过点 E作交于点 F.
(3)【拓展结论,设计新题】如图3,在等边三角形中,点E在直线上,点 D在线段的延长线上,且 ,若 的边长为2, ,求的长.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C A D B D D D A D B
1.C
【分析】本题主要考查了三角形三边关系的判断,熟练掌握三角形三边的不等关系是解题关键.三角形任意一边小于其余两边之和,满足此关系则可组成三角形,据此进一步判断即可.
【详解】解:A:,不能组成三角形,故该选项不正确,不符合题意;
B:,不能组成三角形,故该选项不正确,不符合题意;
C:,能组成三角形,故该选项正确,符合题意;
D:,不能组成三角形,故该选项不正确,不符合题意.
故选:C.
2.A
【分析】本题考查科学记数法表示较小的数,关键是掌握用科学记数法表示数的方法.用科学记数法表示较小的数,一般形式为,其中,为由原数左边起第一个不为零的数字前面的0的个数所决定,由此即可得到答案.
【详解】解:.
故选:A.
3.D
【分析】本题考查了幂的运算,合并同类项;根据同底数幂的乘法,幂的乘方,同底数幂的除法,合并同类项,进行计算即可求解.
【详解】解:A. ,故该选项不正确,不符合题意;
B. ,故该选项不正确,不符合题意;
C. ,故该选项不正确,不符合题意;
D. ,故该选项正确,符合题意;
故选:D
4.B
【分析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称,进行判断即可.
【详解】解:A,C,D选项中的图形都能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
B选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形.
故选:B.
【点睛】本题考查的是轴对称图形的概念,正确掌握相关定义是解题关键.
5.D
【分析】根据为边a和边c的夹角和全等三角形对应角相等解答即可.本题考查全等三角形的性质,掌握全等三角形对应角相等是解题关键.
【详解】解:∵图中的两个三角形全等,且为边a和边c的夹角,
∴.
故选D.
6.D
【分析】本题考查分式的值,解题的关键是正确理解分式有意义的条件、分式的值为零的条件,以及分式方程的解法,本题属于基础题型.把表格中的数据分别代入求解即可.
【详解】解:∵当时,分式无意义,
∴,
∴,故A正确;
当时,分式的值为0,
∴,
∴,故B正确;
当时,分式的值为1,
∴,
∴,
∴,故C正确,D错误.
故选D.
7.D
【分析】本题主要考查了多项式乘多项式、单项式乘多项式、整式运算等知识点,先根据图1和图2,分别用两种方法表示出阴影部分面积,然后列出等式即可;掌握数形结合思想成为解题的关键.
【详解】解:图1中的阴影部分的面积为,
图2中的阴影部分的面积为,
∴.
故选:D.
8.A
【分析】本题主要考查了线段垂直平分线的性质的应用;利用所学的数学知识解决实际问题是一种能力,要注意培养.想到要使凳子到三个人的距离相等是正确解答本题的关键.为使游戏公平,要使凳子到三个人的距离相等,于是利用线段垂直平分线上的点到线段两端的距离相等可知,要放在三边中垂线的交点上.
【详解】解:三角形的三条垂直平分线的交点到三角形各顶点的距离相等,
凳子应放在的三条垂直平分线的交点最适当.
故选:A.
9.D
【分析】本题考查分式方程的实际应用,解题的关键是正确找出等量关系.设乙班每小时植棵树,则甲班每小时植棵树,由甲班植棵树所用的时间与乙班植棵树所用的时间相等,列方程即可求解.
【详解】解:设乙班每小时植棵树,则甲班每小时植棵树,
根据题意可得:,
故选:D.
10.B
【分析】本题考查了轴对称-最短路线问题,关键是将的最小值为转化为.过点C作于点P,交于点E,过点E作于F,则即为的最小值,再根据三角形的面积公式求出的长,即为的最小值.
【详解】解:过点C作于点P,交于点E,过点E作于F,
∵平分,,,
∴,
∴,此时取最小值.
∵的面积为18,,
∴,
∴.
即的最小值为6,
故选B.
11.(-3,-5)
【分析】利用平面内两点关于x轴对称时:横坐标不变,纵坐标互为相反数,进行求解.
【详解】解:P(-3,5)关于x轴的对称点的坐标是(-3,-5),
故答案为:(-3,-5).
【点睛】本题考查了关于原点对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数;关于原点对称的点,横坐标与纵坐标都互为相反数.
12.
【分析】将代数式化为,将代入代数式并求出代数式的值.
【详解】解:∵,
∴,
∴,
故答案为:.
【点睛】此题考查了代数式的求值,解题的关键在于找出代数式与已知条件的关系,根据已知条件求出代数式中的未知项,代入求解.
13.多(五)边形的外角和为或五边形内角和为
【分析】本题考查多边形的内角和与外角和,正确作出辅助线是解题的关键.连接,利用三角形内角和可得出五边形的内角和,利用邻补角的定义可求出五边形的外角和.
【详解】解:如图,连接,
的内角和的内角和的内角和
.
∵,,,,,
∴
.
∴从图可得多(五)边形的外角和为或五边形内角和为.
故答案为:多(五)边形的外角和为或五边形内角和为.
14. ; .
【分析】()将代入根据分式分母不为即可得到答案;
()将代入根据分式方程,解方程即可;
此题考查了分式有意义的条件和解分式方程,解题的关键是熟练掌握知识点的应用.
【详解】()当时,分式为,
要使分式有意义,则,解得:,
故答案为:;
()当时,分式方程为,
则,
∴,
经检验,是原分式方程的解,
故答案为:.
15.(1);(2)无解
【分析】本题主要考查了整式混合运算,解分式方程,解题的关键是熟练掌握运算法则,准确计算.
(1)根据分式混合运算法则进行计算即可;
(2)先去分母,变分式方程为整式方程,然后解整式方程,最后进行检验即可.
【详解】解:(1)
;
(2),
解:去分母得:,
去括号得:,
移项,合并同类项得:,
解得:,
检验:把代入得:,
∴是原方程的增根,
∴原方程无解.
16.;证明见解析
【分析】本题主要考查了全等三角形的判定,解题的关键是熟练掌握三角形全等的判定方法,,,,,.先证明,然后根据证明即可.
【详解】证明:,理由如下
,
即,
在和中,
.
17.见解析
【分析】本题主要考查了轴对称作图,作三角形的中线,解题的关键是先作出点、B、C关于直线的对称点D、E、F,然后顺次连接即可;先作出的中点P,然后再连接即可.
【详解】解:如图,即为所求作的三角形,即为中边上的中线.
18.①:③;分式的基本性质;②:④;去括号时未改变1的符号;③;④分式化简时,若分子分母能因式分解,一定要先因式分解,再进行化简(答案不唯一)
【分析】本题考查分式的减法运算.掌握分式的性质和混合运算法则,是解题的关键.
任务一:①根据异分母加减时需要通分,通分运用的是分式的基本性质进行作答即可;
②去括号时,变号出现问题;
任务二:根据异分母的分式的减法法则,计算即可;
任务三:根据运算法则,提出合理建议即可.
【详解】解:任务一:①:第③步是通分,通分的依据是分式的基本性质;
故答案为:③;分式的基本性质;
②第④步开始出现错误,错误的原因是去括号时未改变1的符号;
故答案为:④;去括号时未改变1的符号;
任务二:③
;
故答案为:;
任务三:分式化简时,若分子分母能因式分解,一定要先因式分解,再进行化简(答案不唯一).
19.见解析
【分析】本题主要考查平行线的性质,等边对等角,全等三角形的判定与性质,过点作交于点,再证明,根据全等三角形的性质即可得到结论;
【详解】证明:过点作交于点,
,
,
在和中,
20.(1)1.7米
(2)1米
【分析】本题考查全等三角形的应用,解题的关键是正确寻找全等三角形全等的条件,灵活运用所学知识解决问题,属于中考常考题型.
(1)过作于点,证明,得到米,即可求解;
(2)由(1)得米,再求解即可.
【详解】(1)过作于点,
在和中,
米
(2)由(1)知:米
故到地面距离为:米.
21.(1)“丰收号”小麦试验田的单位面积产量高;
(2)“丰收号”小麦试验田的边长为.
【分析】()根据题意可以求得两块试验田的面积,从而可以求得哪种小麦的单位面积产量高;
()根据“高的单位面积产量是低的单位面积产量的倍”列出分式方程,解方程即可求解;
本题考查分式的混合运算,分式方程的应用,掌握分式的运算及分式方程的解法是解题的关键.
【详解】(1)解:“丰收号”小麦试验田的单位面积产量为,
“丰收号”小麦试验田的单位面积产量为,
,
,,
∵,
∴,
∴,
答:“丰收号”小麦试验田的单位面积产量高;
(2)解:由题意可得,,
去分母,两边同乘,得,
解得,
经检验,是原方程的解,
∴,
答:“丰收号”小麦试验田的边长为.
22.(1);(2)1
【分析】(1)根据材料(a+b)2=a2+2ab+b2和(a+b)3=a3+3a2b+3ab2+b3展开式,可直接得出的展开式;
(2)根据材料的逆运算可得出答案.
【详解】(1)如图,
则(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
(2)25﹣5×24+10×23﹣10×22+5×2﹣1.
=25+5×24×(﹣1)+10×23×(﹣1)2+10×22×(﹣1)3+5×2×(﹣1)4+(﹣1)5.
=,
=1.
【点睛】本题考查了完全平方公式,学生的观察分析逻辑推理能力,读懂题意并根据所给的式子寻找规律,是快速解题的关键.
23.(1)=,详见解析
(2)=,详见解析
(3),详见解析
【分析】本题主要考查了等边三角形的判定与性质、全等三角形的判定与性质、等腰三角形的性质等知识,
(1)由等腰三角形的性质得,再由等边三角形的性质得,然后证,得,即可得出结论;
(2)过点E作,交于点F,证为等边三角形,得,再证,得,即可得出结论;
(3)过点E作,交的延长线于点F,同(2)得是等边三角形,,则,,即可得出答案;
熟练掌握等边三角形的判定与性质,证明三角形全等是解题的关键.
【详解】(1),理由如下:
∵,
∴,
∵是等边三角形,
∴,
∵点E为的中点,
∴,,
∴,
∵,
∴,
∴,
∴,
∴,
故答案为:;
(2),理由如下:
过点E作,交于点F,
∴,,,
∵是等边三角形,
∴,,
∴,,
∴为等边三角形,,
∴,
∵,
∴,
∴,
在和中,
,
∴,
∴,
∴;
故答案为:;
(3)的长为6;理由如下:
过点E作,交的延长线于点F,如图3所示:
同(2)得:是等边三角形,,
∴,,
∵,
∴,
故答案为:6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
安徽模式2024-2025学年八年级上学期期末数学试卷(二)
考试时间:100分钟 满分:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题
1.下列长度的三条线段能组成三角形的是( )
A.1,2,3.5 B.4,5,9
C.3,5,7 D.5,15,8
2.芜湖水稻种植历史悠久,素有“江南鱼米之乡”的美誉,也曾是“四大米市”之一,所产芜湖大米杍粒细长,晶莹剔透,蒸煮后清香扑鼻,柔韧可口.已知一粒米的重量约0.000021千克,将数据0.000021用科学记数法表示为( )
A. B. C. D.
3.下列运算正确的是( )
A. B.
C. D.
4.数学中有许多精美的曲线.以下是“笛卡尔叶形线”“阿基米德螺线”“三叶玫瑰线”和“星形线”,其中一定不是轴对称图形的是( )
A. B. C. D.
5.图中的两个三角形全等,则等于( )
A. B. C. D.
6.已知分式(,为常数)满足下列表格中的信息,则下列结论错误的是( )
的取值
分式的值 无意义 0 1
A. B.
C. D.
7.通过计算比较图中图①,图②中阴影部分的面积,可以验证的计算式子是( )
A.
B.
C.
D.
8.游戏时,3名同学分别站在三个顶点的位置上、要求在他们中间放一个凳子,谁先坐到凳子上谁获胜,为使游戏公平,则凳子应放置的最适当的位置是在的( )
A.三边垂直平分线的交点 B.三条角平分线的交点
C.三边中线的交点 D.三边上高的交点
9.植树节的起源可以追溯到中国古代“孟春之月,盛德在木”的传统观念,这体现了古人对树木的深深敬仰,某校在“植树节”期间带领学生开展植树活动,甲、乙两班同时开始植树,甲班比乙班每小时多植棵树,植树活动结束时,甲、乙两班同时停止植树,甲班共植棵树,乙班共植棵树,设乙班每小时植棵树,依题意可列方程为( )
A. B. C. D.
10.如图,在锐角三角形中,,的面积为18,平分,若、分别是、上的动点,则的最小值必( )
A.5 B.6 C.7 D.8
第II卷(非选择题)
二、填空题
11.点 P( 3,5)关于x 轴的对称点的坐标为 .
12.若,则多项式的值是 .
13.课本上的这幅插图直观验证了多边形的一条性质,它是: .
14.已知分式.
(1)如果,那么的取值范围是 .
(2)若,且,则的值为 .
三、解答题
15.(1)计算:;(2)解方程:
16.如图,在中,,,,、交于点.在不添加字母和辅助线的情况下,请你在图中找出一对全等三角形并证明.
17.如图,的顶点在正方形网格的格点上.
画关于直线的轴对称图形(不写画法);作中边上的中线(请用无刻度的直尺作图,保留作图痕迹)
18.下面是小彬同学进行分式化简的过程,请认真阅读并完成相应任务.
…………………………①
…………………………②
…………………………③
…………………………④
…………………………⑤
【任务一】填空:
①以上化简步骤中,第______步进行的是分式的通分,通分的依据是______;
②第______步开始出现错误.这一步错误的原因是______;
【任务二】③该分式化简后的正确结果为______
【任务三】④请你根据平时的学习经验,就分式化简时还需要注意的事项给其他同学提一条建议.
19.已知:如图,在中,,点在上,点在边的延长线上,与相交于点.若,求证:.
20.小球悬挂处点到地面的距离是4米,小球从静止状态处开始摆动,摆动到最高点时,测得到的距离为3米,距离地面2.3米.
(1)求小球摆动到垂直于位置时到的距离;
(2)求到地面的距离,写出必要的推理过程.
21.如图,“丰收号”小麦的试验田是边长为的正方形去掉一个边长为m的正方形蓄水池后余下的部分,“丰收号”小麦的试验田是边长为的正方形,两块试验田的小麦都收获了.
(1)哪种小麦的单位面积产量高
(2)若高的单位面积产量是低的单位面积产量的倍,求“丰收号”小麦的试验田的边长.
22.我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应展开式中的系数;第四行的四个数1,3,3,1,恰好对应着展开式中的系数等等.
(1)根据上面的规律,写出的展开式.
(2)利用上面的规律计算:
23.数学是一门充满乐趣、奥妙、又极具探索的学科,对一个人的思维也是一种“挑战”几何图形更是变幻无穷,但只要我们借助图形的直观、特殊情形出发,逐步“从特殊到一般”进行探索,思路和方法自然就会显现出来.下面是一道探索几何图形中线段与数量关系的例子:
已知,在等边三角形中,点E在上,点D 在的延长线上, 且
小星的思路是:
(1)【特殊情况,探索结论】如图1,当点E为的中点时,确定线段与的大小关系, 请你直接写出结论: (填“>”, “<”或“=”);
(2)【特例启发,解答题目】如图2,当点E为边上任意一点时,确定线段与 的大小关系, 请你写出结论: (填“>”,“<”或“=”); 理由如下:(请你将理由补充完整)
证明:过点 E作交于点 F.
(3)【拓展结论,设计新题】如图3,在等边三角形中,点E在直线上,点 D在线段的延长线上,且 ,若 的边长为2, ,求的长.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 C A D B D D D A D B
1.C
【分析】本题主要考查了三角形三边关系的判断,熟练掌握三角形三边的不等关系是解题关键.三角形任意一边小于其余两边之和,满足此关系则可组成三角形,据此进一步判断即可.
【详解】解:A:,不能组成三角形,故该选项不正确,不符合题意;
B:,不能组成三角形,故该选项不正确,不符合题意;
C:,能组成三角形,故该选项正确,符合题意;
D:,不能组成三角形,故该选项不正确,不符合题意.
故选:C.
2.A
【分析】本题考查科学记数法表示较小的数,关键是掌握用科学记数法表示数的方法.用科学记数法表示较小的数,一般形式为,其中,为由原数左边起第一个不为零的数字前面的0的个数所决定,由此即可得到答案.
【详解】解:.
故选:A.
3.D
【分析】本题考查了幂的运算,合并同类项;根据同底数幂的乘法,幂的乘方,同底数幂的除法,合并同类项,进行计算即可求解.
【详解】解:A. ,故该选项不正确,不符合题意;
B. ,故该选项不正确,不符合题意;
C. ,故该选项不正确,不符合题意;
D. ,故该选项正确,符合题意;
故选:D
4.B
【分析】根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴,这时,我们也可以说这个图形关于这条直线(成轴)对称,进行判断即可.
【详解】解:A,C,D选项中的图形都能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
B选项中的图形不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形.
故选:B.
【点睛】本题考查的是轴对称图形的概念,正确掌握相关定义是解题关键.
5.D
【分析】根据为边a和边c的夹角和全等三角形对应角相等解答即可.本题考查全等三角形的性质,掌握全等三角形对应角相等是解题关键.
【详解】解:∵图中的两个三角形全等,且为边a和边c的夹角,
∴.
故选D.
6.D
【分析】本题考查分式的值,解题的关键是正确理解分式有意义的条件、分式的值为零的条件,以及分式方程的解法,本题属于基础题型.把表格中的数据分别代入求解即可.
【详解】解:∵当时,分式无意义,
∴,
∴,故A正确;
当时,分式的值为0,
∴,
∴,故B正确;
当时,分式的值为1,
∴,
∴,
∴,故C正确,D错误.
故选D.
7.D
【分析】本题主要考查了多项式乘多项式、单项式乘多项式、整式运算等知识点,先根据图1和图2,分别用两种方法表示出阴影部分面积,然后列出等式即可;掌握数形结合思想成为解题的关键.
【详解】解:图1中的阴影部分的面积为,
图2中的阴影部分的面积为,
∴.
故选:D.
8.A
【分析】本题主要考查了线段垂直平分线的性质的应用;利用所学的数学知识解决实际问题是一种能力,要注意培养.想到要使凳子到三个人的距离相等是正确解答本题的关键.为使游戏公平,要使凳子到三个人的距离相等,于是利用线段垂直平分线上的点到线段两端的距离相等可知,要放在三边中垂线的交点上.
【详解】解:三角形的三条垂直平分线的交点到三角形各顶点的距离相等,
凳子应放在的三条垂直平分线的交点最适当.
故选:A.
9.D
【分析】本题考查分式方程的实际应用,解题的关键是正确找出等量关系.设乙班每小时植棵树,则甲班每小时植棵树,由甲班植棵树所用的时间与乙班植棵树所用的时间相等,列方程即可求解.
【详解】解:设乙班每小时植棵树,则甲班每小时植棵树,
根据题意可得:,
故选:D.
10.B
【分析】本题考查了轴对称-最短路线问题,关键是将的最小值为转化为.过点C作于点P,交于点E,过点E作于F,则即为的最小值,再根据三角形的面积公式求出的长,即为的最小值.
【详解】解:过点C作于点P,交于点E,过点E作于F,
∵平分,,,
∴,
∴,此时取最小值.
∵的面积为18,,
∴,
∴.
即的最小值为6,
故选B.
11.(-3,-5)
【分析】利用平面内两点关于x轴对称时:横坐标不变,纵坐标互为相反数,进行求解.
【详解】解:P(-3,5)关于x轴的对称点的坐标是(-3,-5),
故答案为:(-3,-5).
【点睛】本题考查了关于原点对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数;关于原点对称的点,横坐标与纵坐标都互为相反数.
12.
【分析】将代数式化为,将代入代数式并求出代数式的值.
【详解】解:∵,
∴,
∴,
故答案为:.
【点睛】此题考查了代数式的求值,解题的关键在于找出代数式与已知条件的关系,根据已知条件求出代数式中的未知项,代入求解.
13.多(五)边形的外角和为或五边形内角和为
【分析】本题考查多边形的内角和与外角和,正确作出辅助线是解题的关键.连接,利用三角形内角和可得出五边形的内角和,利用邻补角的定义可求出五边形的外角和.
【详解】解:如图,连接,
的内角和的内角和的内角和
.
∵,,,,,
∴
.
∴从图可得多(五)边形的外角和为或五边形内角和为.
故答案为:多(五)边形的外角和为或五边形内角和为.
14. ; .
【分析】()将代入根据分式分母不为即可得到答案;
()将代入根据分式方程,解方程即可;
此题考查了分式有意义的条件和解分式方程,解题的关键是熟练掌握知识点的应用.
【详解】()当时,分式为,
要使分式有意义,则,解得:,
故答案为:;
()当时,分式方程为,
则,
∴,
经检验,是原分式方程的解,
故答案为:.
15.(1);(2)无解
【分析】本题主要考查了整式混合运算,解分式方程,解题的关键是熟练掌握运算法则,准确计算.
(1)根据分式混合运算法则进行计算即可;
(2)先去分母,变分式方程为整式方程,然后解整式方程,最后进行检验即可.
【详解】解:(1)
;
(2),
解:去分母得:,
去括号得:,
移项,合并同类项得:,
解得:,
检验:把代入得:,
∴是原方程的增根,
∴原方程无解.
16.;证明见解析
【分析】本题主要考查了全等三角形的判定,解题的关键是熟练掌握三角形全等的判定方法,,,,,.先证明,然后根据证明即可.
【详解】证明:,理由如下
,
即,
在和中,
.
17.见解析
【分析】本题主要考查了轴对称作图,作三角形的中线,解题的关键是先作出点、B、C关于直线的对称点D、E、F,然后顺次连接即可;先作出的中点P,然后再连接即可.
【详解】解:如图,即为所求作的三角形,即为中边上的中线.
18.①:③;分式的基本性质;②:④;去括号时未改变1的符号;③;④分式化简时,若分子分母能因式分解,一定要先因式分解,再进行化简(答案不唯一)
【分析】本题考查分式的减法运算.掌握分式的性质和混合运算法则,是解题的关键.
任务一:①根据异分母加减时需要通分,通分运用的是分式的基本性质进行作答即可;
②去括号时,变号出现问题;
任务二:根据异分母的分式的减法法则,计算即可;
任务三:根据运算法则,提出合理建议即可.
【详解】解:任务一:①:第③步是通分,通分的依据是分式的基本性质;
故答案为:③;分式的基本性质;
②第④步开始出现错误,错误的原因是去括号时未改变1的符号;
故答案为:④;去括号时未改变1的符号;
任务二:③
;
故答案为:;
任务三:分式化简时,若分子分母能因式分解,一定要先因式分解,再进行化简(答案不唯一).
19.见解析
【分析】本题主要考查平行线的性质,等边对等角,全等三角形的判定与性质,过点作交于点,再证明,根据全等三角形的性质即可得到结论;
【详解】证明:过点作交于点,
,
,
在和中,
20.(1)1.7米
(2)1米
【分析】本题考查全等三角形的应用,解题的关键是正确寻找全等三角形全等的条件,灵活运用所学知识解决问题,属于中考常考题型.
(1)过作于点,证明,得到米,即可求解;
(2)由(1)得米,再求解即可.
【详解】(1)过作于点,
在和中,
米
(2)由(1)知:米
故到地面距离为:米.
21.(1)“丰收号”小麦试验田的单位面积产量高;
(2)“丰收号”小麦试验田的边长为.
【分析】()根据题意可以求得两块试验田的面积,从而可以求得哪种小麦的单位面积产量高;
()根据“高的单位面积产量是低的单位面积产量的倍”列出分式方程,解方程即可求解;
本题考查分式的混合运算,分式方程的应用,掌握分式的运算及分式方程的解法是解题的关键.
【详解】(1)解:“丰收号”小麦试验田的单位面积产量为,
“丰收号”小麦试验田的单位面积产量为,
,
,,
∵,
∴,
∴,
答:“丰收号”小麦试验田的单位面积产量高;
(2)解:由题意可得,,
去分母,两边同乘,得,
解得,
经检验,是原方程的解,
∴,
答:“丰收号”小麦试验田的边长为.
22.(1);(2)1
【分析】(1)根据材料(a+b)2=a2+2ab+b2和(a+b)3=a3+3a2b+3ab2+b3展开式,可直接得出的展开式;
(2)根据材料的逆运算可得出答案.
【详解】(1)如图,
则(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
(2)25﹣5×24+10×23﹣10×22+5×2﹣1.
=25+5×24×(﹣1)+10×23×(﹣1)2+10×22×(﹣1)3+5×2×(﹣1)4+(﹣1)5.
=,
=1.
【点睛】本题考查了完全平方公式,学生的观察分析逻辑推理能力,读懂题意并根据所给的式子寻找规律,是快速解题的关键.
23.(1)=,详见解析
(2)=,详见解析
(3),详见解析
【分析】本题主要考查了等边三角形的判定与性质、全等三角形的判定与性质、等腰三角形的性质等知识,
(1)由等腰三角形的性质得,再由等边三角形的性质得,然后证,得,即可得出结论;
(2)过点E作,交于点F,证为等边三角形,得,再证,得,即可得出结论;
(3)过点E作,交的延长线于点F,同(2)得是等边三角形,,则,,即可得出答案;
熟练掌握等边三角形的判定与性质,证明三角形全等是解题的关键.
【详解】(1),理由如下:
∵,
∴,
∵是等边三角形,
∴,
∵点E为的中点,
∴,,
∴,
∵,
∴,
∴,
∴,
∴,
故答案为:;
(2),理由如下:
过点E作,交于点F,
∴,,,
∵是等边三角形,
∴,,
∴,,
∴为等边三角形,,
∴,
∵,
∴,
∴,
在和中,
,
∴,
∴,
∴;
故答案为:;
(3)的长为6;理由如下:
过点E作,交的延长线于点F,如图3所示:
同(2)得:是等边三角形,,
∴,,
∵,
∴,
故答案为:6.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
