初中数学人教版九年级上册 24.1.2 垂直与弦的直径 教学设计
文档属性
| 名称 | 初中数学人教版九年级上册 24.1.2 垂直与弦的直径 教学设计 |

|
|
| 格式 | doc | ||
| 文件大小 | 74.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-12 10:17:10 | ||
图片预览

文档简介
24.1.2垂直与弦的直径
教材来源:初中九年级《数学(上册)》教科书/人民教育出版社
内容来源:初中九年级《数学(上册)》第24 章
主 题:垂直与弦的直径
课 时: 1课时
授课对象:九年级学生
目标确定的依据 :
1.课程标准相关要求:*探索并证明垂径定理。
2. 教材分析 :本节是《圆》这一章的重要内容,也是本章的基础。它揭示了垂直于弦的直径和这条弦及这条弦所对的弧之间的内在关系,是圆的轴对称性的具体化;也是今后证明线段相等、角 相等、 弧相等、 垂直关系的重要依据;同时也为进行圆的有关计算和作图提供了方法和依据。所 以它在教材中处于非常重要的位置。
3.学情分析: 由垂径定理的得出,使学生的认识从感性到理性,从具体到抽象,有助于培养学生思维的严谨性。同时,通过本节课的教学,对学生渗透类比、转化、数形结合、方程、建模等数学思 想和方法,培养学生实验、观察、猜想、抽象、概括、推理等逻辑思维能力和识图能力。
学习目标 :1.探索圆的对称性,进而得到垂直于弦的直径所具有的性质;
2.能够利用垂直于弦的直径的性质解决相关实际问题.
学习重点:垂直于弦的直径所具有的性质以及证明
学习难点:垂直于弦的直径所具有的性质以及证明
学习方法:观察法 演示法 讨论法 讲解法和启发式教学相结合
评价任务:掌握垂径定理及其推论,并会应用其解决实际问题。
学习过程:
一、创设问题情境,激发学生兴趣,引出本节内容
活动1:用纸剪一个圆,沿着圆的任意一条直径对折,重复做几次,你发现了什么?由此你能得到什么结论?(出示:探究圆的性质)
学生动手操作,观察操作结果,可以发现沿着圆的任意一条直径对折,直径两旁的部分能够完全重合,由此可以发现:圆是轴对称图形,任何一条直径所在直线都是它的对称轴.
二、问题引申,探究垂直于弦的直径的性质
活动2:按下面的步骤做一做:
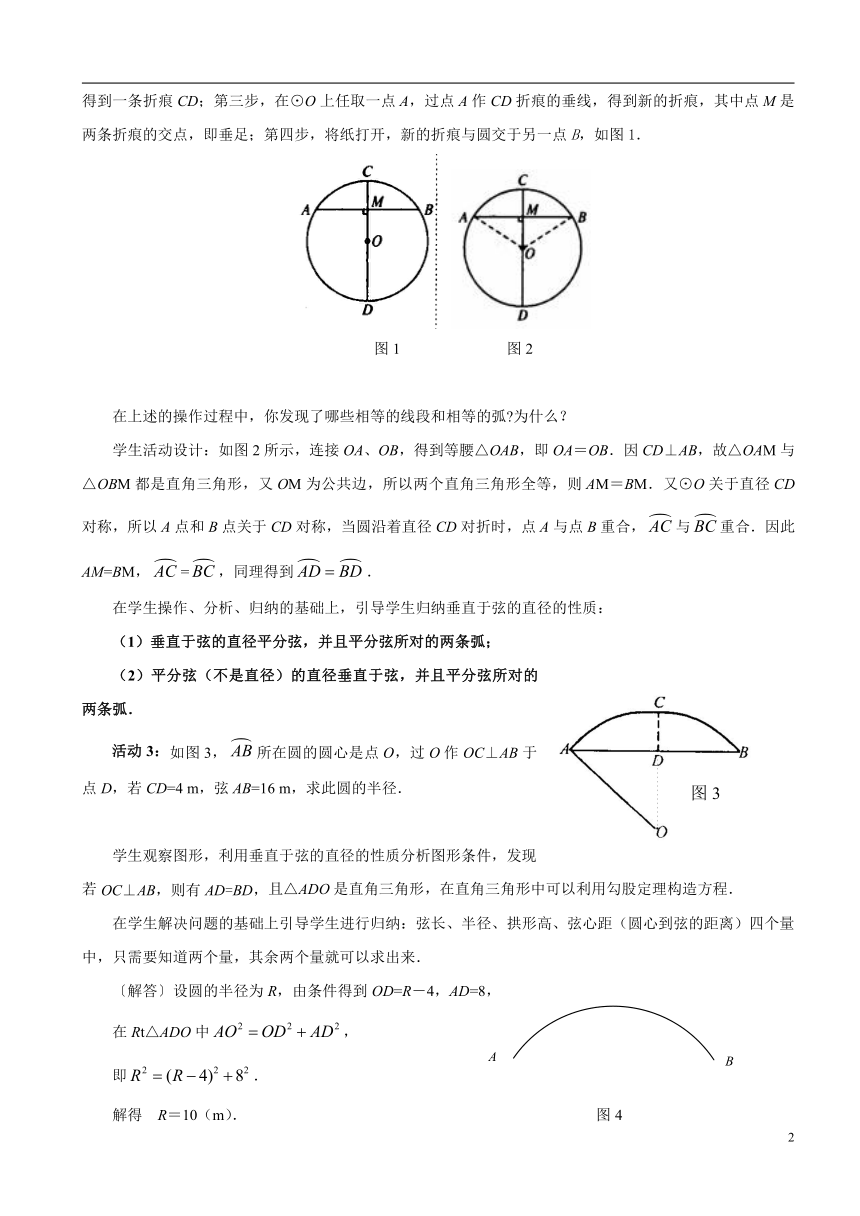
第一步,在一张纸上任意画一个⊙O,沿圆周将圆剪下,把这个圆对折,使圆的两半部分重合;第二步,得到一条折痕CD;第三步,在⊙O上任取一点A,过点A作CD折痕的垂线,得到新的折痕,其中点M是两条折痕的交点,即垂足;第四步,将纸打开,新的折痕与圆交于另一点B,如图1.
图1 图2
在上述的操作过程中,你发现了哪些相等的线段和相等的弧 为什么?
学生活动设计:如图2所示,连接OA、OB,得到等腰△OAB,即OA=OB.因CD⊥AB,故△OAM与△OBM都是直角三角形,又OM为公共边,所以两个直角三角形全等,则AM=BM.又⊙O关于直径CD对称,所以A点和B点关于CD对称,当圆沿着直径CD对折时,点A与点B重合,与重合.因此AM=BM,=,同理得到.
在学生操作、分析、归纳的基础上,引导学生归纳垂直于弦的直径的性质:
(1)垂直于弦的直径平分弦,并且平分弦所对的两条弧;
(2)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
活动3:如图3,所在圆的圆心是点O,过O作OC⊥AB于点D,若CD=4 m,弦AB=16 m,求此圆的半径.
学生观察图形,利用垂直于弦的直径的性质分析图形条件,发现若OC⊥AB,则有AD=BD,且△ADO是直角三角形,在直角三角形中可以利用勾股定理构造方程.
在学生解决问题的基础上引导学生进行归纳:弦长、半径、拱形高、弦心距(圆心到弦的距离)四个量中,只需要知道两个量,其余两个量就可以求出来.
〔解答〕设圆的半径为R,由条件得到OD=R-4,AD=8,
在Rt△ADO中,
即.
解得 R=10(m). 图4
答:此圆的半径是10 m.
活动4:如图4,已知,请你利用尺规作图的方法作出的中点,说出你的作法.
根据基本尺规作图可以发现不能直接作出弧的中点,但是利用垂径定理只需要作出弧所对的弦的垂直平分线,垂直平分线与弧的交点就是弧的中点.
〔解答〕1.连接AB;
2.作AB的中垂线,交 于点C,点C就是所求的点.
三、拓展创新,培养学生思维的灵活性以及创新意识.
活动5 解决下列问题
1.如图5,某条河上有一座圆弧形拱桥ACB,桥下面水面宽度AB为7.2米,桥的最高处点C离水面的高度2.4米.现在有一艘宽3米,船舱顶部为方形并高出水面2米的货船要经过这里,问:这艘船是否能够通过这座拱桥?说明理由.
图5 图6
学生活动:学生根据实际问题,首先分析题意,然后采取一定的策略来说明能否通过这座拱桥,这时要采取一定的比较量,才能说明能否通过,比如,计算一下在上述条件下,在宽度为3米的情况下的高度与2米作比较,若大于2米说明不能经过,否则就可以经过这座拱桥.
〔解答〕如图6,连接AO、GO、CO,由于弧的最高点C是弧AB的中点,所以得到
OC⊥AB,OC⊥GF,
根据勾股定理容易计算
OE=1.5米,
OM=3.6米.
所以ME=2.1米,因此可以通过这座拱桥.
2.银川市某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道.如图7所示,污水水面宽度为60 cm,水面至管道顶部距离为10 cm,问修理人员应准备内径多大的管道
图7 图8
师生活动设计:让学生在探究过程中,进一步把实际问题转化为数学问题,掌握通过作辅助线构造垂径定理的基本结构图,进而发展学生的思维.
〔解答〕
如图8所示,连接OA,过O作OE⊥AB,垂足为E,交圆于F,
则AE=AB = 30 cm.令⊙O的半径为R,
则OA=R,OE=OF-EF=R-10.
在Rt△AEO中,OA2=AE2+OE2,即R2=302+(R-10)2.
解得R =50 cm.
修理人员应准备内径为100 cm的管道.
四、归纳小结、布置作业
1、小结:垂直于弦的直径的性质,圆对称性.
2、作业:第88页练习,习题24.1 第1题,第8题,第9题.
图3
教材来源:初中九年级《数学(上册)》教科书/人民教育出版社
内容来源:初中九年级《数学(上册)》第24 章
主 题:垂直与弦的直径
课 时: 1课时
授课对象:九年级学生
目标确定的依据 :
1.课程标准相关要求:*探索并证明垂径定理。
2. 教材分析 :本节是《圆》这一章的重要内容,也是本章的基础。它揭示了垂直于弦的直径和这条弦及这条弦所对的弧之间的内在关系,是圆的轴对称性的具体化;也是今后证明线段相等、角 相等、 弧相等、 垂直关系的重要依据;同时也为进行圆的有关计算和作图提供了方法和依据。所 以它在教材中处于非常重要的位置。
3.学情分析: 由垂径定理的得出,使学生的认识从感性到理性,从具体到抽象,有助于培养学生思维的严谨性。同时,通过本节课的教学,对学生渗透类比、转化、数形结合、方程、建模等数学思 想和方法,培养学生实验、观察、猜想、抽象、概括、推理等逻辑思维能力和识图能力。
学习目标 :1.探索圆的对称性,进而得到垂直于弦的直径所具有的性质;
2.能够利用垂直于弦的直径的性质解决相关实际问题.
学习重点:垂直于弦的直径所具有的性质以及证明
学习难点:垂直于弦的直径所具有的性质以及证明
学习方法:观察法 演示法 讨论法 讲解法和启发式教学相结合
评价任务:掌握垂径定理及其推论,并会应用其解决实际问题。
学习过程:
一、创设问题情境,激发学生兴趣,引出本节内容
活动1:用纸剪一个圆,沿着圆的任意一条直径对折,重复做几次,你发现了什么?由此你能得到什么结论?(出示:探究圆的性质)
学生动手操作,观察操作结果,可以发现沿着圆的任意一条直径对折,直径两旁的部分能够完全重合,由此可以发现:圆是轴对称图形,任何一条直径所在直线都是它的对称轴.
二、问题引申,探究垂直于弦的直径的性质
活动2:按下面的步骤做一做:
第一步,在一张纸上任意画一个⊙O,沿圆周将圆剪下,把这个圆对折,使圆的两半部分重合;第二步,得到一条折痕CD;第三步,在⊙O上任取一点A,过点A作CD折痕的垂线,得到新的折痕,其中点M是两条折痕的交点,即垂足;第四步,将纸打开,新的折痕与圆交于另一点B,如图1.
图1 图2
在上述的操作过程中,你发现了哪些相等的线段和相等的弧 为什么?
学生活动设计:如图2所示,连接OA、OB,得到等腰△OAB,即OA=OB.因CD⊥AB,故△OAM与△OBM都是直角三角形,又OM为公共边,所以两个直角三角形全等,则AM=BM.又⊙O关于直径CD对称,所以A点和B点关于CD对称,当圆沿着直径CD对折时,点A与点B重合,与重合.因此AM=BM,=,同理得到.
在学生操作、分析、归纳的基础上,引导学生归纳垂直于弦的直径的性质:
(1)垂直于弦的直径平分弦,并且平分弦所对的两条弧;
(2)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.
活动3:如图3,所在圆的圆心是点O,过O作OC⊥AB于点D,若CD=4 m,弦AB=16 m,求此圆的半径.
学生观察图形,利用垂直于弦的直径的性质分析图形条件,发现若OC⊥AB,则有AD=BD,且△ADO是直角三角形,在直角三角形中可以利用勾股定理构造方程.
在学生解决问题的基础上引导学生进行归纳:弦长、半径、拱形高、弦心距(圆心到弦的距离)四个量中,只需要知道两个量,其余两个量就可以求出来.
〔解答〕设圆的半径为R,由条件得到OD=R-4,AD=8,
在Rt△ADO中,
即.
解得 R=10(m). 图4
答:此圆的半径是10 m.
活动4:如图4,已知,请你利用尺规作图的方法作出的中点,说出你的作法.
根据基本尺规作图可以发现不能直接作出弧的中点,但是利用垂径定理只需要作出弧所对的弦的垂直平分线,垂直平分线与弧的交点就是弧的中点.
〔解答〕1.连接AB;
2.作AB的中垂线,交 于点C,点C就是所求的点.
三、拓展创新,培养学生思维的灵活性以及创新意识.
活动5 解决下列问题
1.如图5,某条河上有一座圆弧形拱桥ACB,桥下面水面宽度AB为7.2米,桥的最高处点C离水面的高度2.4米.现在有一艘宽3米,船舱顶部为方形并高出水面2米的货船要经过这里,问:这艘船是否能够通过这座拱桥?说明理由.
图5 图6
学生活动:学生根据实际问题,首先分析题意,然后采取一定的策略来说明能否通过这座拱桥,这时要采取一定的比较量,才能说明能否通过,比如,计算一下在上述条件下,在宽度为3米的情况下的高度与2米作比较,若大于2米说明不能经过,否则就可以经过这座拱桥.
〔解答〕如图6,连接AO、GO、CO,由于弧的最高点C是弧AB的中点,所以得到
OC⊥AB,OC⊥GF,
根据勾股定理容易计算
OE=1.5米,
OM=3.6米.
所以ME=2.1米,因此可以通过这座拱桥.
2.银川市某居民区一处圆形下水管道破裂,修理人员准备更换一段新管道.如图7所示,污水水面宽度为60 cm,水面至管道顶部距离为10 cm,问修理人员应准备内径多大的管道
图7 图8
师生活动设计:让学生在探究过程中,进一步把实际问题转化为数学问题,掌握通过作辅助线构造垂径定理的基本结构图,进而发展学生的思维.
〔解答〕
如图8所示,连接OA,过O作OE⊥AB,垂足为E,交圆于F,
则AE=AB = 30 cm.令⊙O的半径为R,
则OA=R,OE=OF-EF=R-10.
在Rt△AEO中,OA2=AE2+OE2,即R2=302+(R-10)2.
解得R =50 cm.
修理人员应准备内径为100 cm的管道.
四、归纳小结、布置作业
1、小结:垂直于弦的直径的性质,圆对称性.
2、作业:第88页练习,习题24.1 第1题,第8题,第9题.
图3
同课章节目录
