7.1.1 两条直线相交(课件)2024-2025七年级下册数学人教(2024)版
文档属性
| 名称 | 7.1.1 两条直线相交(课件)2024-2025七年级下册数学人教(2024)版 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-02 09:27:20 | ||
图片预览







文档简介
(共22张PPT)
7.1.1 两条直线相交
任课教师:XXX
班级:XX年XX班
第7章 相交线与平行线
学习目标
1.理解对顶角和邻补角的概念,能够在图形中准确识别对顶角和邻补角。
2.掌握对顶角相等这一性质,并应用该性质进行角度的计算和推理。
3.通过对相交线相关问题的探究,学会观察图形中角与角之间的关系,提高识图能力
目录
贰
内容教学
叁
例题讲解
肆
课后作业
壹
新课导入
新课导入
新课导入
问题一:观察下列图片,你能否得到相交的直线。
新课导入
问题二:如果把剪刀抽象成一个几何图形,会得到一个什么几何图形?
动手画一画,讨论一下
新课导入
问题三:如图7.1-1、取两根本条a、b、将它们钉在一 起,并把它们想象成两条直线,就得到一个相交线的模型。在转动木条的过程中,它们所成的角也在变化、你能发现这些角之间不变的关系吗
内容教学
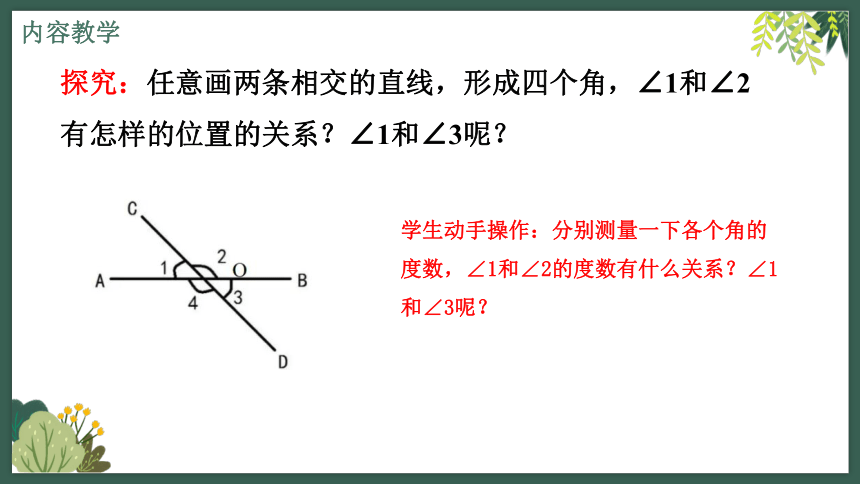
探究:任意画两条相交的直线,形成四个角,∠1和∠2有怎样的位置的关系?∠1和∠3呢?
学生动手操作:分别测量一下各个角的度数,∠1和∠2的度数有什么关系?∠1和∠3呢?
内容教学
探究:任意画两条相交的直线,形成四个角,∠1和∠2有怎样的位置的关系?∠1和∠3呢?
学生动手操作:分别测量一下各个角的度数,∠1和∠2的度数有什么关系?∠1和∠3呢?
探究:任意画两条相交的直线,形成四个角,∠1和∠2有怎样的位置的关系?∠1和∠3呢?
学生动手操作:分别测量一下各个角的度数,∠1和∠2的度数有什么关系?∠1和∠3呢?
内容教学
探究:任意画两条相交的直线,形成四个角,∠1和∠2有怎样的位置的关系?∠1和∠3呢?
课堂反思:利用信息技术工具,改变两条直线相交所成的角的大小,上述关系还保持吗?为什么?
思考:图中还有没有其他的邻补角和对顶角?
归纳总结:
1.∠1和∠2有一条公共边 OC ,它们的另一边互为 反向延长线 (∠1和∠2互补),具有这种位置关系的两个角,互为邻补角。
2.∠1和∠3有一个公共点O,并且∠1的两边分别是∠3两边的 反向延长线 ,具有这种位置关系的两个角,互为对顶角。
3.对顶角的性质:对顶角 相等 。
内容教学
归纳总结:
1.∠1和∠2有一条公共边OC,它们的另一边互为反向延长线 (∠1和∠2互补),具有这种位置关系的两个角,互为邻补角。
2.∠1和∠3有一个公共点O,并且∠1的两边分别是∠3两边的 反向延长线,具有这种位置关系的两个角,互为对顶角。
3.对顶角的性质:对顶角相等。
例题讲解
例题讲解
例1 如图所示,直线a、b相交,∠1=40°,求∠2,∠3,∠4的度数?
解:由∠1和∠2互为邻补角,得
∠2=180°-∠1=189°-40°=140°。
由对顶角相等,得
∠3=∠1=40°,∠2=∠4=140°
课堂练习
1.如图,与是对顶角的为( )
A、
B、
C、
D、
D
课堂练习
2.如图是一把剪刀,在使用过程中,若∠COD增加20°,则
( )
A.减少20° B.增加20° C.不变 D.增加40°
B
课堂练习
3.如图,直线AB、CD相交于点O,∠AOD=2∠BOD,若∠BOE=40°,则∠COE的度数为( )
A.40° B.50° C.60° D.80°
D
课堂练习
4.如图,直线AB、CD、EF相交于点O,∠BOE的对顶角是 ,∠COF的邻补角是 .若∠AOC:∠AOE=2:3,∠EOD=130°,则∠AOC= ,∠BOC= .
∠COF
∠COE、DOF
20°
160°
课堂练习
5.如图,两条直线AB,CD 交于点O,OF平分∠BOD,若∠1=46°,则∠2= .
23°
课堂练习
6.如图,直线AB,CD,EF相交于点O.
(1)写出∠AOC,∠BOE的邻补角;
(2)写出∠DOA,∠EOC的对顶角;
(3)如果∠AOC=50°,求∠BOD、∠COB..
(1)∠AOC的邻补角是∠COB,∠DOA;∠BOE的邻补角是:∠AOE,∠BOF
(2)∠DOA的对顶角是∠COB,∠EOC的对顶角是∠DOF
(3)∠BOD=50°,∠COB=130°;
课后作业布置
ENTER YOUR TITLE
课后作业布置
作业参考:
书籍汇编配套练习
感谢各位同学观看
TO FEEL THE FLAME OF DREAMING AND TO FEEL THE MOMENT OFDANCING,
WHEN ALL THE ROMANCE IS FAR AWAY,THE ETERNITY IS ALWAYS THERE.
任课教师:XXX
班级:XX年XX班
7.1.1 两条直线相交
任课教师:XXX
班级:XX年XX班
第7章 相交线与平行线
学习目标
1.理解对顶角和邻补角的概念,能够在图形中准确识别对顶角和邻补角。
2.掌握对顶角相等这一性质,并应用该性质进行角度的计算和推理。
3.通过对相交线相关问题的探究,学会观察图形中角与角之间的关系,提高识图能力
目录
贰
内容教学
叁
例题讲解
肆
课后作业
壹
新课导入
新课导入
新课导入
问题一:观察下列图片,你能否得到相交的直线。
新课导入
问题二:如果把剪刀抽象成一个几何图形,会得到一个什么几何图形?
动手画一画,讨论一下
新课导入
问题三:如图7.1-1、取两根本条a、b、将它们钉在一 起,并把它们想象成两条直线,就得到一个相交线的模型。在转动木条的过程中,它们所成的角也在变化、你能发现这些角之间不变的关系吗
内容教学
探究:任意画两条相交的直线,形成四个角,∠1和∠2有怎样的位置的关系?∠1和∠3呢?
学生动手操作:分别测量一下各个角的度数,∠1和∠2的度数有什么关系?∠1和∠3呢?
内容教学
探究:任意画两条相交的直线,形成四个角,∠1和∠2有怎样的位置的关系?∠1和∠3呢?
学生动手操作:分别测量一下各个角的度数,∠1和∠2的度数有什么关系?∠1和∠3呢?
探究:任意画两条相交的直线,形成四个角,∠1和∠2有怎样的位置的关系?∠1和∠3呢?
学生动手操作:分别测量一下各个角的度数,∠1和∠2的度数有什么关系?∠1和∠3呢?
内容教学
探究:任意画两条相交的直线,形成四个角,∠1和∠2有怎样的位置的关系?∠1和∠3呢?
课堂反思:利用信息技术工具,改变两条直线相交所成的角的大小,上述关系还保持吗?为什么?
思考:图中还有没有其他的邻补角和对顶角?
归纳总结:
1.∠1和∠2有一条公共边 OC ,它们的另一边互为 反向延长线 (∠1和∠2互补),具有这种位置关系的两个角,互为邻补角。
2.∠1和∠3有一个公共点O,并且∠1的两边分别是∠3两边的 反向延长线 ,具有这种位置关系的两个角,互为对顶角。
3.对顶角的性质:对顶角 相等 。
内容教学
归纳总结:
1.∠1和∠2有一条公共边OC,它们的另一边互为反向延长线 (∠1和∠2互补),具有这种位置关系的两个角,互为邻补角。
2.∠1和∠3有一个公共点O,并且∠1的两边分别是∠3两边的 反向延长线,具有这种位置关系的两个角,互为对顶角。
3.对顶角的性质:对顶角相等。
例题讲解
例题讲解
例1 如图所示,直线a、b相交,∠1=40°,求∠2,∠3,∠4的度数?
解:由∠1和∠2互为邻补角,得
∠2=180°-∠1=189°-40°=140°。
由对顶角相等,得
∠3=∠1=40°,∠2=∠4=140°
课堂练习
1.如图,与是对顶角的为( )
A、
B、
C、
D、
D
课堂练习
2.如图是一把剪刀,在使用过程中,若∠COD增加20°,则
( )
A.减少20° B.增加20° C.不变 D.增加40°
B
课堂练习
3.如图,直线AB、CD相交于点O,∠AOD=2∠BOD,若∠BOE=40°,则∠COE的度数为( )
A.40° B.50° C.60° D.80°
D
课堂练习
4.如图,直线AB、CD、EF相交于点O,∠BOE的对顶角是 ,∠COF的邻补角是 .若∠AOC:∠AOE=2:3,∠EOD=130°,则∠AOC= ,∠BOC= .
∠COF
∠COE、DOF
20°
160°
课堂练习
5.如图,两条直线AB,CD 交于点O,OF平分∠BOD,若∠1=46°,则∠2= .
23°
课堂练习
6.如图,直线AB,CD,EF相交于点O.
(1)写出∠AOC,∠BOE的邻补角;
(2)写出∠DOA,∠EOC的对顶角;
(3)如果∠AOC=50°,求∠BOD、∠COB..
(1)∠AOC的邻补角是∠COB,∠DOA;∠BOE的邻补角是:∠AOE,∠BOF
(2)∠DOA的对顶角是∠COB,∠EOC的对顶角是∠DOF
(3)∠BOD=50°,∠COB=130°;
课后作业布置
ENTER YOUR TITLE
课后作业布置
作业参考:
书籍汇编配套练习
感谢各位同学观看
TO FEEL THE FLAME OF DREAMING AND TO FEEL THE MOMENT OFDANCING,
WHEN ALL THE ROMANCE IS FAR AWAY,THE ETERNITY IS ALWAYS THERE.
任课教师:XXX
班级:XX年XX班
同课章节目录
