中位线的性质定理

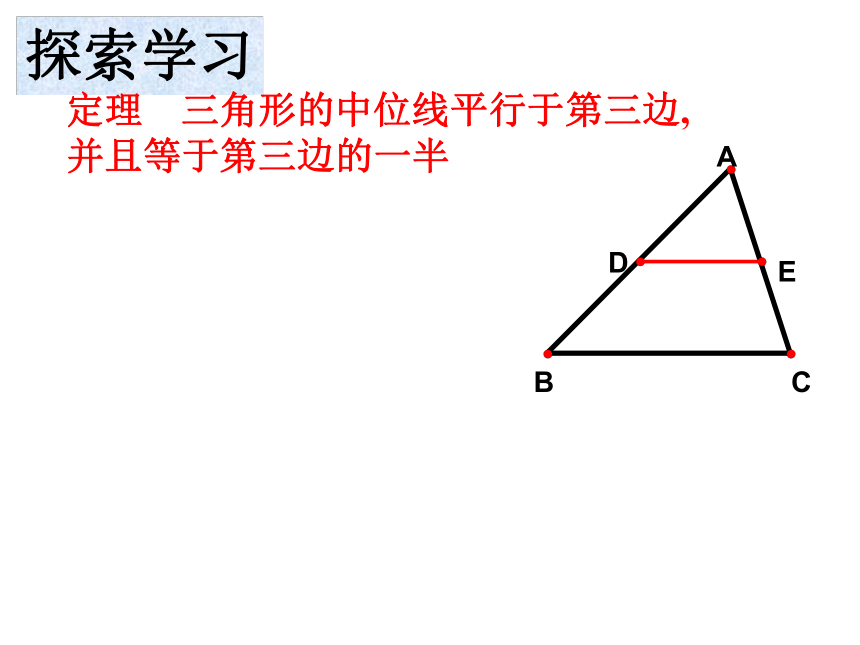
课件14张PPT。三角形中位线的性质定理内丘二中 崔月婷 应用与拓展ABCDE探索学习定理 三角形的中位线平行于第三边,
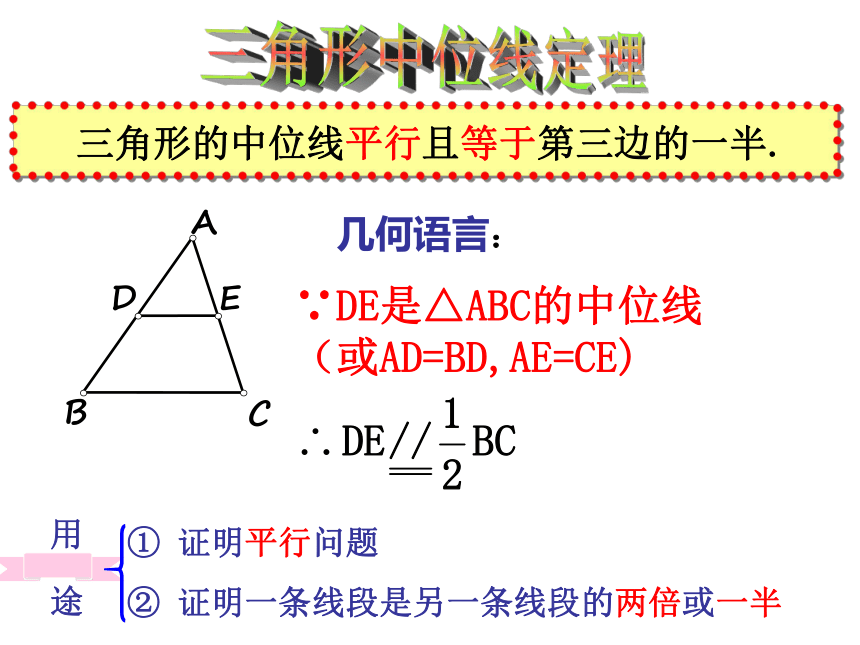
并且等于第三边的一半三角形中位线定理 三角形的中位线平行且等于第三边的一半.几何语言：∵DE是△ABC的中位线（或AD=BD,AE=CE)① 证明平行问题
② 证明一条线段是另一条线段的两倍或一半用 途课前热身------折纸游戏你能做到吗?

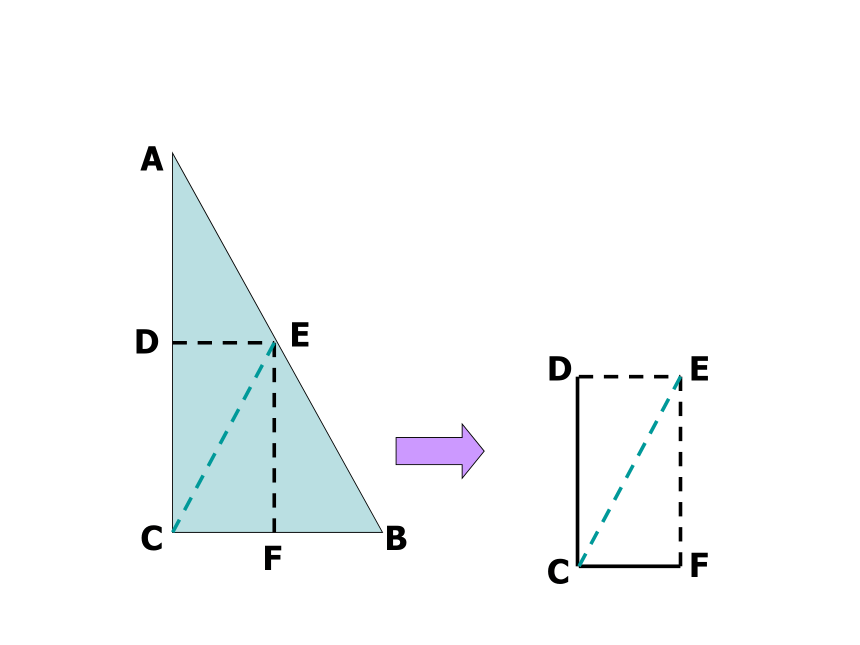
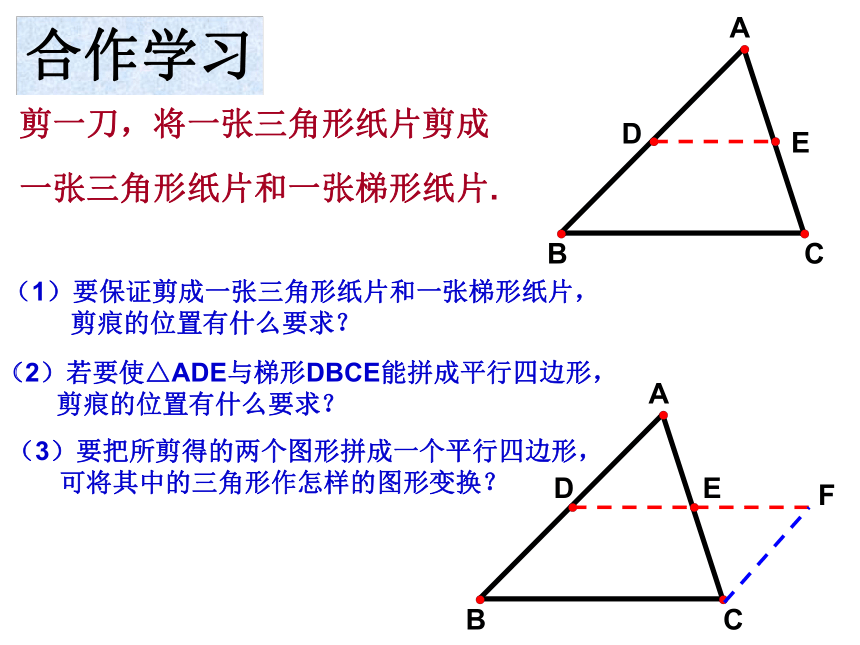
1. 用一张直角三角形形状的纸片,你能折叠成面积减半的长方形吗?ABCDE合作学习剪一刀，将一张三角形纸片剪成
一张三角形纸片和一张梯形纸片.（1）要保证剪成一张三角形纸片和一张梯形纸片，
剪痕的位置有什么要求？（2）若要使△ADE与梯形DBCE能拼成平行四边形，
剪痕的位置有什么要求？ （3）要把所剪得的两个图形拼成一个平行四边形，
可将其中的三角形作怎样的图形变换？ 已知：如图，DE是△ABC的中位线.
求证： 证明：如图，以点E为旋转中心，把⊿ADE绕点E，按顺时针方向旋转180゜，得到⊿CFE ABCDEF得到⊿CFE，⊿ADE≌⊿CFE.∴∠ADE=∠F，AD=CF，DE=EF∴AB∥CF 又∵BD=AD=CF, ∴四边形BCFD是平行四边形 已知：如图，DE是△ABC的中位线.
求证： 证明：如图，延长DE到F，使EF=DE，
连接CF∴∠ADE=∠F，AD=CF，∴AB∥CF 又∵BD=AD=CF, ∴四边形BCFD是平行四边形 ABCDEF∵DE=EF,AE=EC, ∠AED= ∠CEF∴⊿ADE≌⊿CFEEFABCDEF(1) △DEF的周长与 △ABC的周长有什么关系?(2) 面积呢?△DEF的周长是 △ABC周长的一半四分之一在三角形ＡＢＣ中，Ｄ、E、F为ＡＢ、ＡＣ、ＢＣ的中点，则合作学习证明：如图，连接AC∵EF是△ABC的中位线同理得： ∴四边形EFGH是平行四边形①有中点连线而无三角形,要作辅助线产生三角形②有三角形而无中位线,要连结两边中点得中位线合作学习从例题中你能得到什么结论？ 顺次连接四边形各边中点的线段组成一个平行四边形方法点拨：
在处理问题时,要求同时出现三角形及中位线
①有中点连线而无三角形,要作辅助线产生三角形
②有三角形而无中位线,要连结两边中点得中位线定 理 应 用：⑴定理为证明平行关系提供了新的工具
⑵定理为证明一条线段是另一条线段的2倍或 一半提供了一个新的途径