2025年中考数学专项复习-函数压轴题专项突破4 二次函数中的面积问题 课件(共46张PPT)
文档属性
| 名称 | 2025年中考数学专项复习-函数压轴题专项突破4 二次函数中的面积问题 课件(共46张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 13:44:03 | ||
图片预览





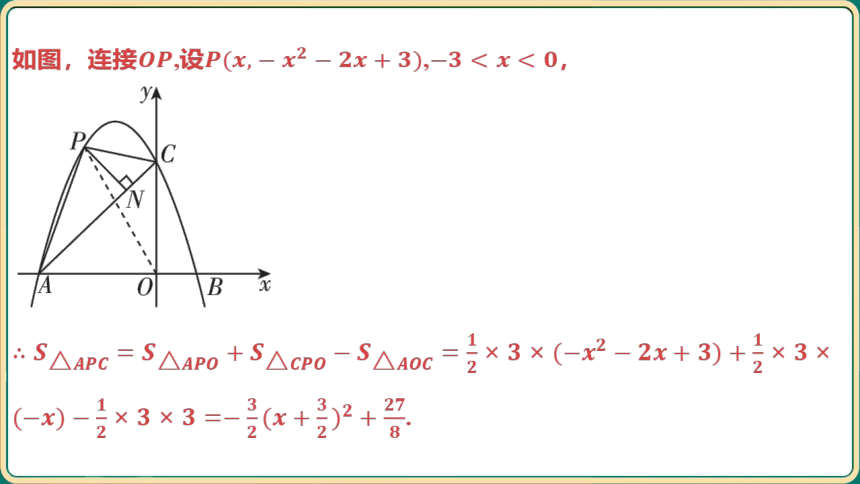
文档简介
(共46张PPT)
函数压轴题专项突破
中考压轴题专项突破
培优专项
二次函数中的面积问题
2025年中考数学一轮复习
例 如图,二次函数的图象与 轴交于
点,,顶点为,点在抛物线上(不与, 重
合),连接,, .
(1)二次函数的解析式为_____________,直线 的解
析式为__________;
(2)若的面积为,则点 的坐标为____________
_____.
或
提分特训
1.[2024福建中考] 如图,已知二次函数 的
图象与轴交于,两点,与轴交于点,其中 ,
.
(1)求二次函数的表达式;
[答案] 将,分别代入,得
解得
故二次函数的表达式为 .
(2)若是二次函数图象上的一点,且点在第二象限,线段交 轴于点
,的面积是的面积的2倍,求点 的坐标.
[答案] 设, 点在第二象限,, .
依题意,得,即, .
, .
由,解得, (舍去),
点的坐标为 .
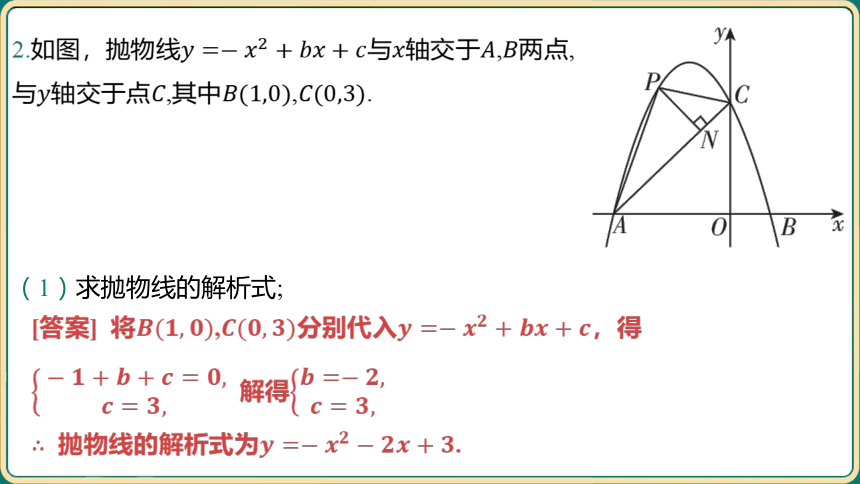
2.如图,抛物线与轴交于, 两点,
与轴交于点,其中, .
(1)求抛物线的解析式;
[答案] 将,分别代入 ,得
解得
抛物线的解析式为 .
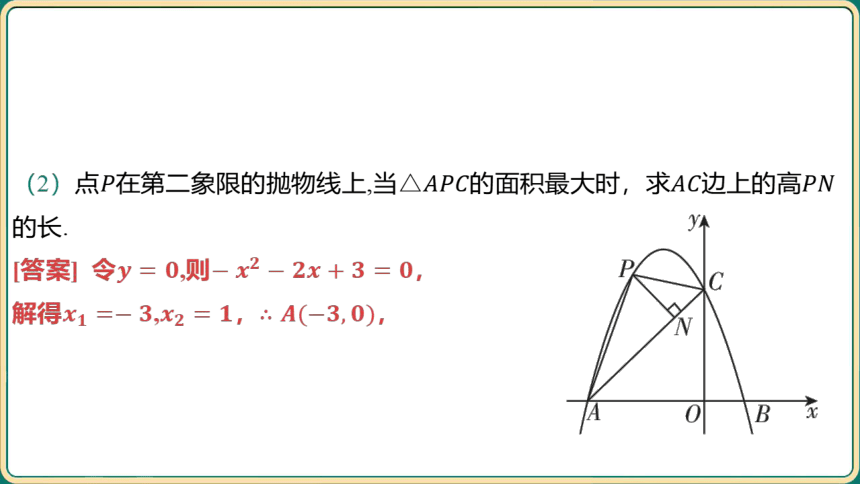
(2)点在第二象限的抛物线上,当的面积最大时,求边上的高
的长.
[答案] 令,则 ,
解得,, ,
如图,连接,设, ,
.
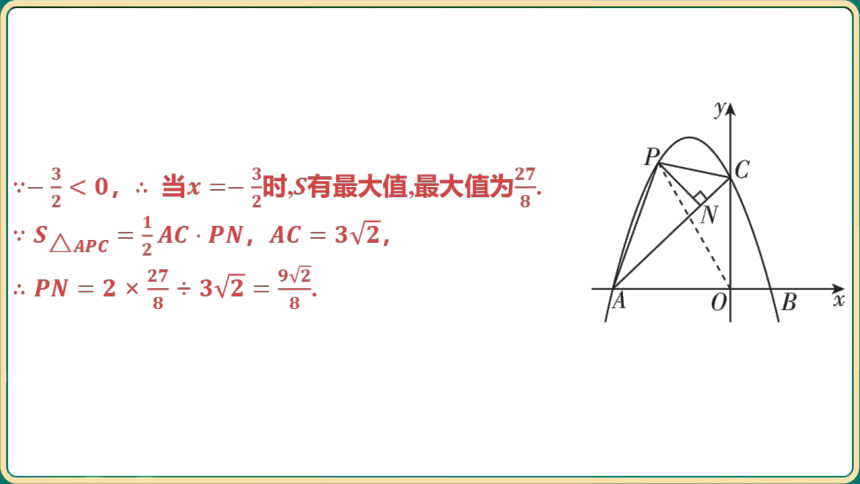
, 当时,有最大值,最大值为 .
, ,
.
3.如图,抛物线交轴于,两点,交轴于点 ,连接
,,点为抛物线上一动点,若,求点 的坐标.
[答案] 如图,过点作,交抛物线于点,交 轴
于点,则 .
在中,当时, ,
.
又 ,
直线的解析式为 .
,
设直线的解析式为 .
直线过点 ,
直线的解析式为 ,
.
联立,得解得或
.
把直线向上平移4个单位长度得到直线 ,并与抛物线
分别交于点,,由,可知,点, 符合题意.
联立,得
解得或
, ,
综上所述,点的坐标为, 或
.
4.如图,抛物线与 轴交
于,两点,与轴交于点,点
在抛物线上,点 是抛物线在第四象限内的一个动
点,过点作轴交直线于点,连接 ,
,,设点的横坐标为 .
(1)求抛物线的函数表达式;
[答案] 把,分别代入 ,
得
解得
抛物线的函数表达式为 .
(2)求四边形面积的最大值及此时点 的坐标.
[答案] ,解得, ,
点的坐标为 .
设直线的表达式为,把, 分别代入,
得解得
直线的表达式为 .
点是抛物线在第四象限内的一个动点,轴交直线于点 ,
设, ,
设交轴与点 .
.
易知 ,
,
.
,
当时, 有最大值,
.
此时 .
图(1)
5.如图(1),抛物线与轴交于点
和点(点在原点的左侧,点 在原点的右侧),且
.在轴上有一动点,过点
作直线轴,交抛物线于点 .
(1)求点 的坐标及抛物线的表达式;
[答案] 易知抛物线的对称轴为直线 ,
, .
将代入,得 ,
,
抛物线的表达式为 .
(2)如图(2),连接,若 ,求此时点 的坐标;
图(2)
[答案] 由题意,设点的坐标为 ,
则 .
, .
,
,
(舍去)或 ,
.
图(3)
(3)如图(3),连接并延长交轴于点,连接 ,
记的面积为,的面积为,若 ,求
此时点 的坐标.
[答案] 由题意,设点的坐标为 .
设直线的表达式为 ,
则解得
故直线的表达式为 ,
当时, ,
故点的坐标为,则, .
,
,
,
,
,即 或
.
当时,解得 ,不合题意,舍去;
当时,解得, (舍去).
综上所述,此时点的坐标为 .
6.抛物线与轴交于点,,与 轴交于
点 .
(1)求抛物线的表达式及顶点 的坐标.
[答案] 把,代入 ,
得解得
抛物线的表达式为 .
,
顶点的坐标为 .
(2)点为轴左侧抛物线上一点,以点为顶点且形状大小与抛物线 相同
的抛物线交轴于点,连接,,,是否存在点 ,使得
若存在,请求出点的坐标,并说明抛物线是抛物线 如何
进行图形变换得到的;若不存在,请说明理由.
[答案] 存在.
, .
将代入,得 ,
,即 ,
,
或 .
设 .
①当抛物线开口向下时,则 .
.将代入 ,
整理得 ,
解得(舍去)或 .
当时, ,
,
,由 先向左平移3个单位长度,
再向下平移9个单位长度得到.
.将代入 ,
整理得, ,
此方程无解,这种情况不存在.
②当抛物线开口向上时,则 .
.将代入 ,
整理得,解得 ,
当时, ,
,
,由关于 轴对称后,先向左平移7个单位长度,
再向下平移41个单位长度得到.
.将代入 ,
整理得,解得 (不合题意,舍去).
综上,,由 先向左平移3个单位长度,再向下平移9个单位长度
得到;,由关于 轴对称后,先向左平移7个单位长度,再向
下平移41个单位长度得到.
7.如图,在平面直角坐标系中,直线
与抛物线交于, 两
点,点在轴上,点的纵坐标为5,点 是直
线下方的抛物线上的一动点(不与点,
重合),过点作轴的垂线交直线于点 ,
作于点 .
(1)求抛物线的解析式.
[答案] 在中,当时,,当时, ,
, .
将,分别代入 中,
得解得
抛物线的解析式为 .
(2)设点的横坐标为 .
①用含的代数式表示线段的长,并求出线段 长的最大值.
[答案] 如图,设直线交轴于点,则点 ,
,
.
易得 轴,
,
.
点的横坐标为, 轴,
, ,
,
.
, ,
当时,取得最大值,且最大值为 .
②连接,线段把分成两个三角形,是否存在 的值,使这两个
三角形的面积比为 若存在,求出 的值;若不存在,请说明理由.
[答案] 如图,过点作于点,
过点作,交 的延长线
于点 ,
由①可知, , ,
在 中,
当时,解得 ;
当时,解得 .
综上,满足题意的 的值为0或3.
.
又 ,
,
8.已知二次函数的图象经过,两点,其中 ,
,为常数,且 .
(1)求, 的值.
[答案] 二次函数的图象经过点 ,
,
由题意知点,关于抛物线的对称轴(直线 )对称,
.
,
.
(2)若该二次函数的最小值是,且它的图象与轴交于点,
(点在点的左侧),与轴交于点 .
①求该二次函数的解析式,并直接写出点, 的坐标.
[答案] , ,
,
,解得 .
,, ,
,
该二次函数的解析式为 .
, .
②如图,在轴左侧该二次函数的图象上有一动点,过点作 轴的垂线,
垂足为,与直线交于点,连接,,.在点右侧是否存在点 ,
使?若存在,求此时点 的横坐标;若不存在,请说明理由.
[答案] 设直线的解析式为 ,
将, 分别代入,
得解得
直线的解析式为 .
如图,过点作于点 .
设,则, ,
则, ,
.
,, ,
.
,
,整理,得 ,
解得,,且满足 .
点的横坐标为或 .
函数压轴题专项突破
中考压轴题专项突破
培优专项
二次函数中的面积问题
2025年中考数学一轮复习
例 如图,二次函数的图象与 轴交于
点,,顶点为,点在抛物线上(不与, 重
合),连接,, .
(1)二次函数的解析式为_____________,直线 的解
析式为__________;
(2)若的面积为,则点 的坐标为____________
_____.
或
提分特训
1.[2024福建中考] 如图,已知二次函数 的
图象与轴交于,两点,与轴交于点,其中 ,
.
(1)求二次函数的表达式;
[答案] 将,分别代入,得
解得
故二次函数的表达式为 .
(2)若是二次函数图象上的一点,且点在第二象限,线段交 轴于点
,的面积是的面积的2倍,求点 的坐标.
[答案] 设, 点在第二象限,, .
依题意,得,即, .
, .
由,解得, (舍去),
点的坐标为 .
2.如图,抛物线与轴交于, 两点,
与轴交于点,其中, .
(1)求抛物线的解析式;
[答案] 将,分别代入 ,得
解得
抛物线的解析式为 .
(2)点在第二象限的抛物线上,当的面积最大时,求边上的高
的长.
[答案] 令,则 ,
解得,, ,
如图,连接,设, ,
.
, 当时,有最大值,最大值为 .
, ,
.
3.如图,抛物线交轴于,两点,交轴于点 ,连接
,,点为抛物线上一动点,若,求点 的坐标.
[答案] 如图,过点作,交抛物线于点,交 轴
于点,则 .
在中,当时, ,
.
又 ,
直线的解析式为 .
,
设直线的解析式为 .
直线过点 ,
直线的解析式为 ,
.
联立,得解得或
.
把直线向上平移4个单位长度得到直线 ,并与抛物线
分别交于点,,由,可知,点, 符合题意.
联立,得
解得或
, ,
综上所述,点的坐标为, 或
.
4.如图,抛物线与 轴交
于,两点,与轴交于点,点
在抛物线上,点 是抛物线在第四象限内的一个动
点,过点作轴交直线于点,连接 ,
,,设点的横坐标为 .
(1)求抛物线的函数表达式;
[答案] 把,分别代入 ,
得
解得
抛物线的函数表达式为 .
(2)求四边形面积的最大值及此时点 的坐标.
[答案] ,解得, ,
点的坐标为 .
设直线的表达式为,把, 分别代入,
得解得
直线的表达式为 .
点是抛物线在第四象限内的一个动点,轴交直线于点 ,
设, ,
设交轴与点 .
.
易知 ,
,
.
,
当时, 有最大值,
.
此时 .
图(1)
5.如图(1),抛物线与轴交于点
和点(点在原点的左侧,点 在原点的右侧),且
.在轴上有一动点,过点
作直线轴,交抛物线于点 .
(1)求点 的坐标及抛物线的表达式;
[答案] 易知抛物线的对称轴为直线 ,
, .
将代入,得 ,
,
抛物线的表达式为 .
(2)如图(2),连接,若 ,求此时点 的坐标;
图(2)
[答案] 由题意,设点的坐标为 ,
则 .
, .
,
,
(舍去)或 ,
.
图(3)
(3)如图(3),连接并延长交轴于点,连接 ,
记的面积为,的面积为,若 ,求
此时点 的坐标.
[答案] 由题意,设点的坐标为 .
设直线的表达式为 ,
则解得
故直线的表达式为 ,
当时, ,
故点的坐标为,则, .
,
,
,
,
,即 或
.
当时,解得 ,不合题意,舍去;
当时,解得, (舍去).
综上所述,此时点的坐标为 .
6.抛物线与轴交于点,,与 轴交于
点 .
(1)求抛物线的表达式及顶点 的坐标.
[答案] 把,代入 ,
得解得
抛物线的表达式为 .
,
顶点的坐标为 .
(2)点为轴左侧抛物线上一点,以点为顶点且形状大小与抛物线 相同
的抛物线交轴于点,连接,,,是否存在点 ,使得
若存在,请求出点的坐标,并说明抛物线是抛物线 如何
进行图形变换得到的;若不存在,请说明理由.
[答案] 存在.
, .
将代入,得 ,
,即 ,
,
或 .
设 .
①当抛物线开口向下时,则 .
.将代入 ,
整理得 ,
解得(舍去)或 .
当时, ,
,
,由 先向左平移3个单位长度,
再向下平移9个单位长度得到.
.将代入 ,
整理得, ,
此方程无解,这种情况不存在.
②当抛物线开口向上时,则 .
.将代入 ,
整理得,解得 ,
当时, ,
,
,由关于 轴对称后,先向左平移7个单位长度,
再向下平移41个单位长度得到.
.将代入 ,
整理得,解得 (不合题意,舍去).
综上,,由 先向左平移3个单位长度,再向下平移9个单位长度
得到;,由关于 轴对称后,先向左平移7个单位长度,再向
下平移41个单位长度得到.
7.如图,在平面直角坐标系中,直线
与抛物线交于, 两
点,点在轴上,点的纵坐标为5,点 是直
线下方的抛物线上的一动点(不与点,
重合),过点作轴的垂线交直线于点 ,
作于点 .
(1)求抛物线的解析式.
[答案] 在中,当时,,当时, ,
, .
将,分别代入 中,
得解得
抛物线的解析式为 .
(2)设点的横坐标为 .
①用含的代数式表示线段的长,并求出线段 长的最大值.
[答案] 如图,设直线交轴于点,则点 ,
,
.
易得 轴,
,
.
点的横坐标为, 轴,
, ,
,
.
, ,
当时,取得最大值,且最大值为 .
②连接,线段把分成两个三角形,是否存在 的值,使这两个
三角形的面积比为 若存在,求出 的值;若不存在,请说明理由.
[答案] 如图,过点作于点,
过点作,交 的延长线
于点 ,
由①可知, , ,
在 中,
当时,解得 ;
当时,解得 .
综上,满足题意的 的值为0或3.
.
又 ,
,
8.已知二次函数的图象经过,两点,其中 ,
,为常数,且 .
(1)求, 的值.
[答案] 二次函数的图象经过点 ,
,
由题意知点,关于抛物线的对称轴(直线 )对称,
.
,
.
(2)若该二次函数的最小值是,且它的图象与轴交于点,
(点在点的左侧),与轴交于点 .
①求该二次函数的解析式,并直接写出点, 的坐标.
[答案] , ,
,
,解得 .
,, ,
,
该二次函数的解析式为 .
, .
②如图,在轴左侧该二次函数的图象上有一动点,过点作 轴的垂线,
垂足为,与直线交于点,连接,,.在点右侧是否存在点 ,
使?若存在,求此时点 的横坐标;若不存在,请说明理由.
[答案] 设直线的解析式为 ,
将, 分别代入,
得解得
直线的解析式为 .
如图,过点作于点 .
设,则, ,
则, ,
.
,, ,
.
,
,整理,得 ,
解得,,且满足 .
点的横坐标为或 .
同课章节目录
