2025年中考数学专项复习-函数压轴题专项突破9 二次函数中的定点、定直线问题 课件(共36张PPT)
文档属性
| 名称 | 2025年中考数学专项复习-函数压轴题专项突破9 二次函数中的定点、定直线问题 课件(共36张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 00:00:00 | ||
图片预览






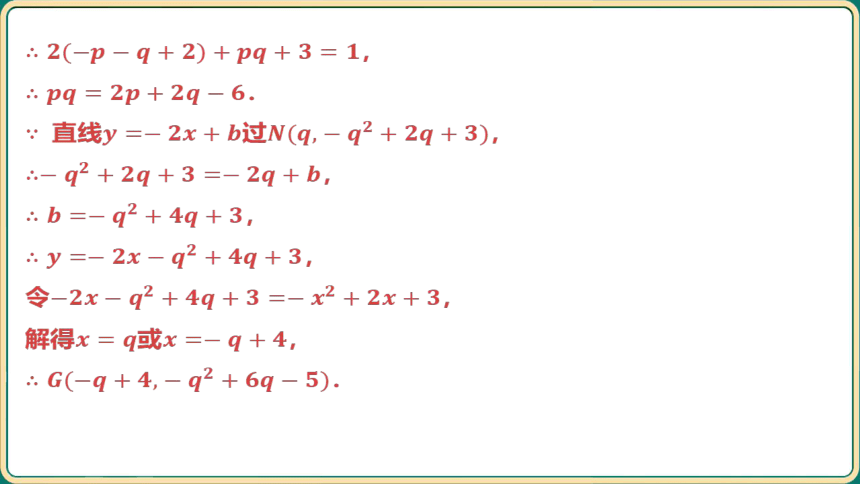



文档简介
(共36张PPT)
函数压轴题专项突破
中考压轴题专项突破
培优专项
二次函数中的定点、定直线问题
2025年中考数学一轮复习
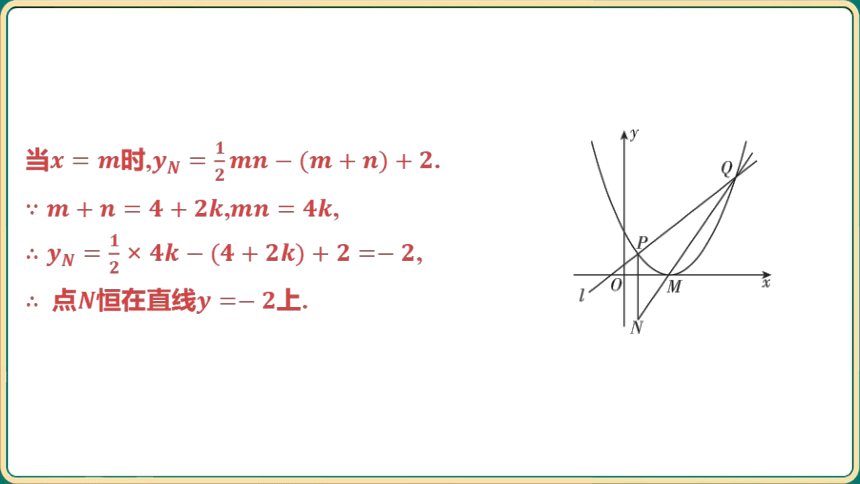
例1 如图,抛物线的顶点为 ,直线
与抛物线交于,两点(点在点 的
左侧),过点且与轴平行的直线与直线相交于点 ,
判断点 是否在一条定直线上,如果是,请求出该直线的
解析式;如果不是,请说明理由.
[答案] ,
设点, ,
由 ,
得 ,
, ,
由,,可得直线 的解析式为
,
当时, .
, ,
,
点恒在直线 上.
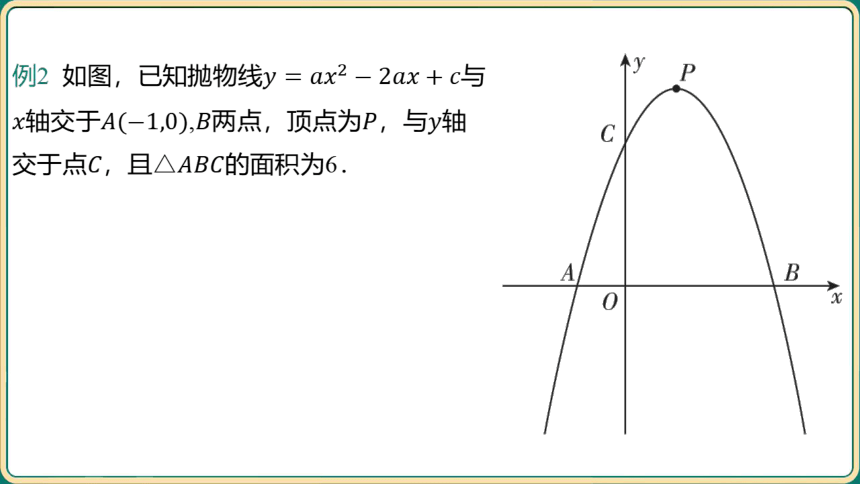
例2 如图,已知抛物线 与
轴交于,两点,顶点为,与 轴
交于点,且 的面积为6.
(1)求抛物线的对称轴和解析式;
[答案] ,
抛物线的对称轴为直线 .
把代入 ,
得 ,
,
.
令,得 ,
,
或 ,
,, .
的面积为6,
,
,
.
把代入,得 ,
解得 ,
抛物线的解析式为 .
(2)若过定点的直线交抛物线于,两点(点在点 右侧),过点
的直线与抛物线交于点,求证:直线 必过定点.
证明:设, .
设直线的解析式为 ,
解得
直线的解析式为 .
直线过定点 ,
,
.
直线过 ,
,
,
,
令 ,
解得或 ,
.
设直线的解析式为,把 ,
分别代入 ,
得
解得
直线的解析式为 .
,
直线的解析式为 ,
当时, ,
直线必过定点 .
提分特训
1.已知抛物线与轴交于点,对称轴是直线 .直线
与抛物线交于,两点(点在点的左侧),点是直线 下方
抛物线上的一个动点,点 在抛物线对称轴上.
(1)求抛物线的表达式;
[答案] 将代入 ,
可得 .
对称轴是直线 ,
,
,
抛物线的表达式是 .
(2)求证:当四边形是平行四边形时,不论为何值,点 的坐标不变.
证明: 直线与抛物线交于, 两点,
,
整理,得 ,
.
如图,连接,交于点 .
四边形 是平行四边形,
,
,
,
,
.
点在抛物线 上,
,
点的坐标为 ,
即不论为何值,点 的坐标不变.
2.我们不妨约定:在平面直角坐标系中,若某函数图象上至少存在不同的两
点关于轴对称,则把该函数称为“函数”,其图象上关于 轴对称的不同两
点叫做一对“ 点”.根据该约定,完成下列各题.
(1)关于的函数(,是常数)是“ 函数”吗?如果是,指出
它有多少对“ 点”;如果不是,请说明理由.
[答案] 当时,有 ,
此时图象上存在关于 轴对称的点,
时,是“函数”,且有无数对“ 点”.
当时,假设图象上存在关于 轴对称的点,
设其中一点为,则其关于轴的对称点为 ,
,
,与 矛盾,
不存在,
时,不是“ 函数”.
(注:“是”与“不是”“ 函数”,要辩证地去看待,不同条件会有不同的结论)
(2)若关于的“函数”(,且,, 是常数)的图
象经过坐标原点,且与直线(,,且, 是常
数)交于,两点,当,满足 时,
直线 是否总经过某一定点?若经过某一定点,求出该定点的坐标;否则,
请说明理由.
[答案] 直线总经过定点 .
函数的图象过原点, .
是“函数”,, .
联立直线和抛物线的表达式,得
整理,得 ,
则, .
由 ,
化简,得 ,
, ,
,
当时, ,
直线总经过定点 .
3.[2024漳州质检] 在平面直角坐标系中,点 在抛物线
上.
(1)求抛物线 的对称轴.
[答案] 点在抛物线 上,
,
,
,
抛物线的对称轴为直线 .
(2)若 ,
①不管取任何实数,抛物线上的三个点,, 中至
少有两个点在轴的上方,求 的取值范围.
[答案] 当时,抛物线 .
根据无论取任何实数,三个点中至少有两个点在 轴的上方,可分以下
两种情况进行讨论.
.当抛物线与 轴没有交点或只有一个交点时,符合题意.
此时 ,
,
.
.当抛物线与轴有两个不同的交点时, .
设两个交点的横坐标分别为, ,
当时,,,中至少有两个点在 轴
的上方,
, .
, ,
, .
综上所述,的取值范围是 .
②平移抛物线得到抛物线,过点,且其顶点为,过点 作直线
(不与直线重合)交抛物线于,两点(点在点 左侧),直线
与直线交于点.求证:点 在一条定直线上.
证明:由平移抛物线得到抛物线,抛物线的顶点为原点 可知抛物
线 ,
抛物线经过点,,, 抛物线 .
设,,直线的解析式为 ,
解得
直线的解析式为 .
直线经过点 ,
.
同理,直线的解析式为,直线的解析式为 .
直线与相交于点 ,如图,
.
联立得解得
,, .
,
点在定直线 上.
4.[2024成都中考] 如图,在平面直角坐标系 中,抛物线
与轴交于,两点(点在点 的左侧),其顶
点为, 是抛物线第四象限上一点.
备用图
(1)求线段 的长.
[答案] 令,得 ,
解得, ,
, ,
.
(2)当时,若的面积与的面积相等,求 的值.
[答案] 当时, .
.
如图,过点作轴于点 .
设 ,
则直线的解析式为 ,
.
过点作轴交于点,则 ,
.
,
,
,
解得(舍去), ,
, .
(3)延长交轴于点,当时,将沿 方向平移得到
.将抛物线平移得到抛物线,使得点,都落在抛物线 上.试判断
抛物线与 是否交于某个定点.若是,求出该定点的坐标;若不是,请说明理由.
[答案] 抛物线与抛物线 交于某个定点.
设 .
点在轴上,且, .
将沿方向平移得到,且点,在抛物线 上,
易知抛物线与的平移方式相同,即将抛物线向右平移 个
单位长度,向上平移个单位长度,得到抛物线 ,
抛物线的解析式为 .
令 ,其中
,
整理,得 ,
又, ,
,
,
.
故抛物线与交于定点 .
函数压轴题专项突破
中考压轴题专项突破
培优专项
二次函数中的定点、定直线问题
2025年中考数学一轮复习
例1 如图,抛物线的顶点为 ,直线
与抛物线交于,两点(点在点 的
左侧),过点且与轴平行的直线与直线相交于点 ,
判断点 是否在一条定直线上,如果是,请求出该直线的
解析式;如果不是,请说明理由.
[答案] ,
设点, ,
由 ,
得 ,
, ,
由,,可得直线 的解析式为
,
当时, .
, ,
,
点恒在直线 上.
例2 如图,已知抛物线 与
轴交于,两点,顶点为,与 轴
交于点,且 的面积为6.
(1)求抛物线的对称轴和解析式;
[答案] ,
抛物线的对称轴为直线 .
把代入 ,
得 ,
,
.
令,得 ,
,
或 ,
,, .
的面积为6,
,
,
.
把代入,得 ,
解得 ,
抛物线的解析式为 .
(2)若过定点的直线交抛物线于,两点(点在点 右侧),过点
的直线与抛物线交于点,求证:直线 必过定点.
证明:设, .
设直线的解析式为 ,
解得
直线的解析式为 .
直线过定点 ,
,
.
直线过 ,
,
,
,
令 ,
解得或 ,
.
设直线的解析式为,把 ,
分别代入 ,
得
解得
直线的解析式为 .
,
直线的解析式为 ,
当时, ,
直线必过定点 .
提分特训
1.已知抛物线与轴交于点,对称轴是直线 .直线
与抛物线交于,两点(点在点的左侧),点是直线 下方
抛物线上的一个动点,点 在抛物线对称轴上.
(1)求抛物线的表达式;
[答案] 将代入 ,
可得 .
对称轴是直线 ,
,
,
抛物线的表达式是 .
(2)求证:当四边形是平行四边形时,不论为何值,点 的坐标不变.
证明: 直线与抛物线交于, 两点,
,
整理,得 ,
.
如图,连接,交于点 .
四边形 是平行四边形,
,
,
,
,
.
点在抛物线 上,
,
点的坐标为 ,
即不论为何值,点 的坐标不变.
2.我们不妨约定:在平面直角坐标系中,若某函数图象上至少存在不同的两
点关于轴对称,则把该函数称为“函数”,其图象上关于 轴对称的不同两
点叫做一对“ 点”.根据该约定,完成下列各题.
(1)关于的函数(,是常数)是“ 函数”吗?如果是,指出
它有多少对“ 点”;如果不是,请说明理由.
[答案] 当时,有 ,
此时图象上存在关于 轴对称的点,
时,是“函数”,且有无数对“ 点”.
当时,假设图象上存在关于 轴对称的点,
设其中一点为,则其关于轴的对称点为 ,
,
,与 矛盾,
不存在,
时,不是“ 函数”.
(注:“是”与“不是”“ 函数”,要辩证地去看待,不同条件会有不同的结论)
(2)若关于的“函数”(,且,, 是常数)的图
象经过坐标原点,且与直线(,,且, 是常
数)交于,两点,当,满足 时,
直线 是否总经过某一定点?若经过某一定点,求出该定点的坐标;否则,
请说明理由.
[答案] 直线总经过定点 .
函数的图象过原点, .
是“函数”,, .
联立直线和抛物线的表达式,得
整理,得 ,
则, .
由 ,
化简,得 ,
, ,
,
当时, ,
直线总经过定点 .
3.[2024漳州质检] 在平面直角坐标系中,点 在抛物线
上.
(1)求抛物线 的对称轴.
[答案] 点在抛物线 上,
,
,
,
抛物线的对称轴为直线 .
(2)若 ,
①不管取任何实数,抛物线上的三个点,, 中至
少有两个点在轴的上方,求 的取值范围.
[答案] 当时,抛物线 .
根据无论取任何实数,三个点中至少有两个点在 轴的上方,可分以下
两种情况进行讨论.
.当抛物线与 轴没有交点或只有一个交点时,符合题意.
此时 ,
,
.
.当抛物线与轴有两个不同的交点时, .
设两个交点的横坐标分别为, ,
当时,,,中至少有两个点在 轴
的上方,
, .
, ,
, .
综上所述,的取值范围是 .
②平移抛物线得到抛物线,过点,且其顶点为,过点 作直线
(不与直线重合)交抛物线于,两点(点在点 左侧),直线
与直线交于点.求证:点 在一条定直线上.
证明:由平移抛物线得到抛物线,抛物线的顶点为原点 可知抛物
线 ,
抛物线经过点,,, 抛物线 .
设,,直线的解析式为 ,
解得
直线的解析式为 .
直线经过点 ,
.
同理,直线的解析式为,直线的解析式为 .
直线与相交于点 ,如图,
.
联立得解得
,, .
,
点在定直线 上.
4.[2024成都中考] 如图,在平面直角坐标系 中,抛物线
与轴交于,两点(点在点 的左侧),其顶
点为, 是抛物线第四象限上一点.
备用图
(1)求线段 的长.
[答案] 令,得 ,
解得, ,
, ,
.
(2)当时,若的面积与的面积相等,求 的值.
[答案] 当时, .
.
如图,过点作轴于点 .
设 ,
则直线的解析式为 ,
.
过点作轴交于点,则 ,
.
,
,
,
解得(舍去), ,
, .
(3)延长交轴于点,当时,将沿 方向平移得到
.将抛物线平移得到抛物线,使得点,都落在抛物线 上.试判断
抛物线与 是否交于某个定点.若是,求出该定点的坐标;若不是,请说明理由.
[答案] 抛物线与抛物线 交于某个定点.
设 .
点在轴上,且, .
将沿方向平移得到,且点,在抛物线 上,
易知抛物线与的平移方式相同,即将抛物线向右平移 个
单位长度,向上平移个单位长度,得到抛物线 ,
抛物线的解析式为 .
令 ,其中
,
整理,得 ,
又, ,
,
,
.
故抛物线与交于定点 .
同课章节目录
