2025年中考数学专项复习-几何压轴题专项突破12 “手拉手”模型 课件(共14张PPT)
文档属性
| 名称 | 2025年中考数学专项复习-几何压轴题专项突破12 “手拉手”模型 课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 13:54:28 | ||
图片预览



文档简介
(共14张PPT)
几何压轴题专项突破
中考压轴题专项突破
“手拉手”模型
2025年中考数学一轮复习
图示 说明 基本结论
全等 模型 情形1: ________________________________________________________________________________ 1., , ; 2.将绕点 旋转,直线 , 交于点 ,所 夹锐角为 . 1.点,, 不共
线时,有
(情形1中,
和
均为等腰三角
形);
图示 说明 基本结论
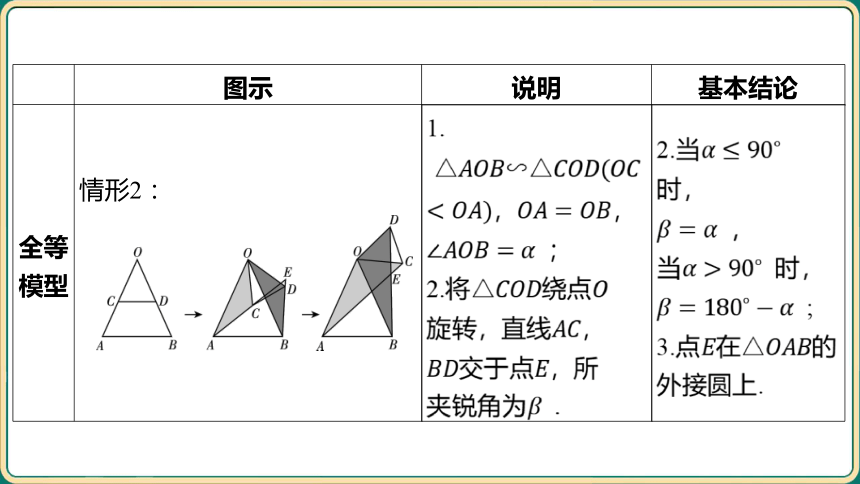
全等 模型 情形2: _________________________________________________________________________________ 1. , , ; 2.将绕点 旋转,直线 , 交于点 ,所 夹锐角为 . 2.当 时,
,
当 时,
;
3.点在 的
外接圆上.
图示 说明 基本结论
相似 模型 情形1: ______________________________________________________________________________________ 1. (两三角形重 合), , ; 2.将绕点 旋转,直线 , 交于点 ,所 夹锐角为 . 1.点,, 不共
线时,有
(情形1中,
和
均为等腰三角
形);
图示 说明 基本结论
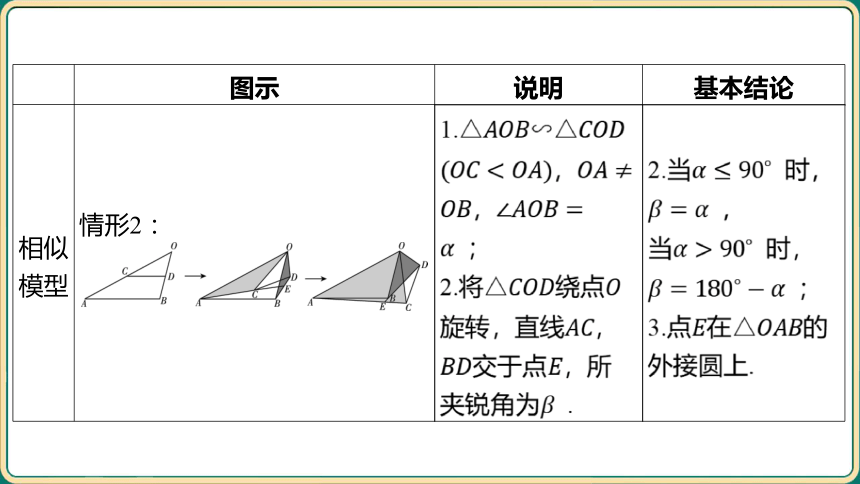
相似 模型 情形2: _______________________________________________________________________________________ 1. , , ; 2.将绕点 旋转,直线 , 交于点 ,所 夹锐角为 . 2.当 时,
,
当 时,
;
3.点在 的
外接圆上.
(第1题)
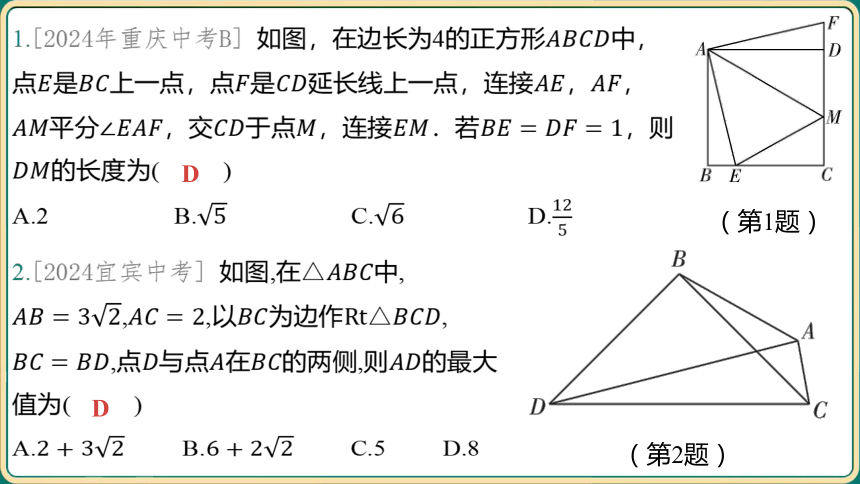
1.[2024年重庆中考B] 如图,在边长为4的正方形 中,
点是上一点,点是延长线上一点,连接, ,
平分,交于点,连接.若 ,则
的长度为( )
D
A.2 B. C. D.
(第2题)
2.[2024宜宾中考] 如图,在 中,
,,以为边作 ,
,点与点在的两侧,则 的最大
值为( )
D
A. B. C.5 D.8
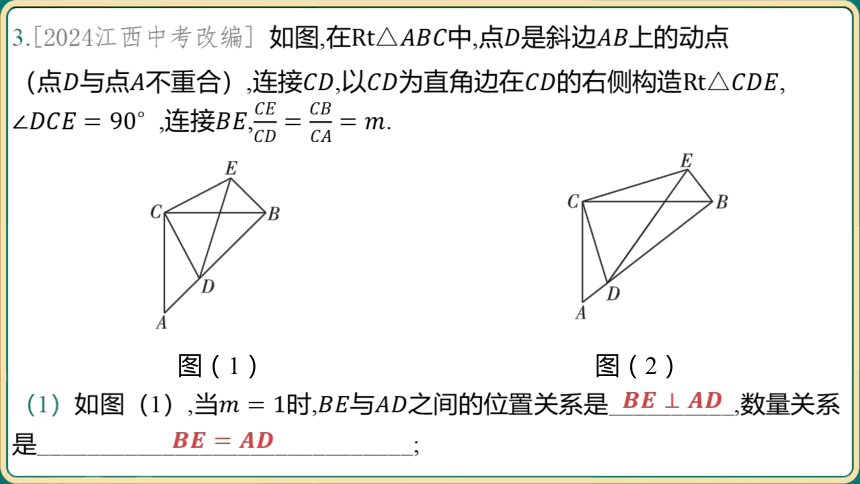
3.[2024江西中考改编] 如图,在中,点是斜边 上的动点
(点与点不重合),连接,以为直角边在的右侧构造 ,
,连接, .
图(1)
图(2)
(1)如图(1),当时,与 之间的位置关系是__________,数量关系
是______________________________;
(2)如图(2),当时,猜想与 之间的位置关系和数量关系,并证明
猜想.
图(2)
[答案] , .
证明: , ,
.
又 ,
,
, ,
.
,
,
即 ,
.
图(2)
4.在学习“旋转”这一重要的平面图形变换时,李老师设计了如下的问题,让同学
们进行探究.如图(1),在中, ,,点是边
上一点,,过点作交于点,将绕点 沿逆时针方向旋
转 .
图(1)
图(2)
备用图
(1)将旋转至如图(2)的位置时,连接,.求证: .
证明:在题图(1)中, 在中, , ,
,
,
,
, .
在题图(2)中, ,
,即 ,
,
, .
图(2)
(2)将旋转至,,三点在同一条直线上时,求线段 的长.
[答案] 由(1),得 ,
,, .
,
,
.
当将旋转至,,三点在同一条直线上时, .
图(2)
①如图(1),在中, ,, ,
图(1)
,
.
, ,
.
②如图(2),易求得, .
图(2)
, ,
.
综上所述,的长为或 .
几何压轴题专项突破
中考压轴题专项突破
“手拉手”模型
2025年中考数学一轮复习
图示 说明 基本结论
全等 模型 情形1: ________________________________________________________________________________ 1., , ; 2.将绕点 旋转,直线 , 交于点 ,所 夹锐角为 . 1.点,, 不共
线时,有
(情形1中,
和
均为等腰三角
形);
图示 说明 基本结论
全等 模型 情形2: _________________________________________________________________________________ 1. , , ; 2.将绕点 旋转,直线 , 交于点 ,所 夹锐角为 . 2.当 时,
,
当 时,
;
3.点在 的
外接圆上.
图示 说明 基本结论
相似 模型 情形1: ______________________________________________________________________________________ 1. (两三角形重 合), , ; 2.将绕点 旋转,直线 , 交于点 ,所 夹锐角为 . 1.点,, 不共
线时,有
(情形1中,
和
均为等腰三角
形);
图示 说明 基本结论
相似 模型 情形2: _______________________________________________________________________________________ 1. , , ; 2.将绕点 旋转,直线 , 交于点 ,所 夹锐角为 . 2.当 时,
,
当 时,
;
3.点在 的
外接圆上.
(第1题)
1.[2024年重庆中考B] 如图,在边长为4的正方形 中,
点是上一点,点是延长线上一点,连接, ,
平分,交于点,连接.若 ,则
的长度为( )
D
A.2 B. C. D.
(第2题)
2.[2024宜宾中考] 如图,在 中,
,,以为边作 ,
,点与点在的两侧,则 的最大
值为( )
D
A. B. C.5 D.8
3.[2024江西中考改编] 如图,在中,点是斜边 上的动点
(点与点不重合),连接,以为直角边在的右侧构造 ,
,连接, .
图(1)
图(2)
(1)如图(1),当时,与 之间的位置关系是__________,数量关系
是______________________________;
(2)如图(2),当时,猜想与 之间的位置关系和数量关系,并证明
猜想.
图(2)
[答案] , .
证明: , ,
.
又 ,
,
, ,
.
,
,
即 ,
.
图(2)
4.在学习“旋转”这一重要的平面图形变换时,李老师设计了如下的问题,让同学
们进行探究.如图(1),在中, ,,点是边
上一点,,过点作交于点,将绕点 沿逆时针方向旋
转 .
图(1)
图(2)
备用图
(1)将旋转至如图(2)的位置时,连接,.求证: .
证明:在题图(1)中, 在中, , ,
,
,
,
, .
在题图(2)中, ,
,即 ,
,
, .
图(2)
(2)将旋转至,,三点在同一条直线上时,求线段 的长.
[答案] 由(1),得 ,
,, .
,
,
.
当将旋转至,,三点在同一条直线上时, .
图(2)
①如图(1),在中, ,, ,
图(1)
,
.
, ,
.
②如图(2),易求得, .
图(2)
, ,
.
综上所述,的长为或 .
同课章节目录
