2025年中考数学专项复习-几何压轴题专项突破16 圆综合题 课件(共49张PPT)
文档属性
| 名称 | 2025年中考数学专项复习-几何压轴题专项突破16 圆综合题 课件(共49张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 13:53:43 | ||
图片预览


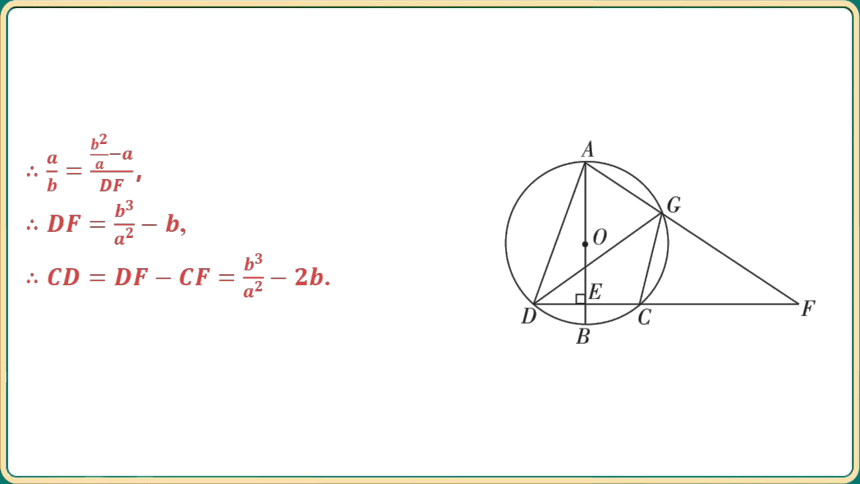

文档简介
(共49张PPT)
几何压轴题专项突破
中考压轴题专项突破
圆综合题
2025年中考数学一轮复习
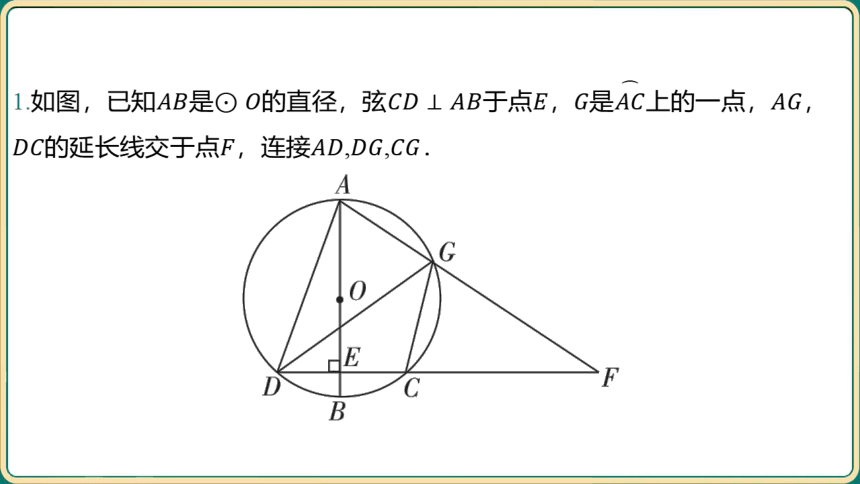
1.如图,已知是的直径,弦于点,是上的一点, ,
的延长线交于点,连接,, .
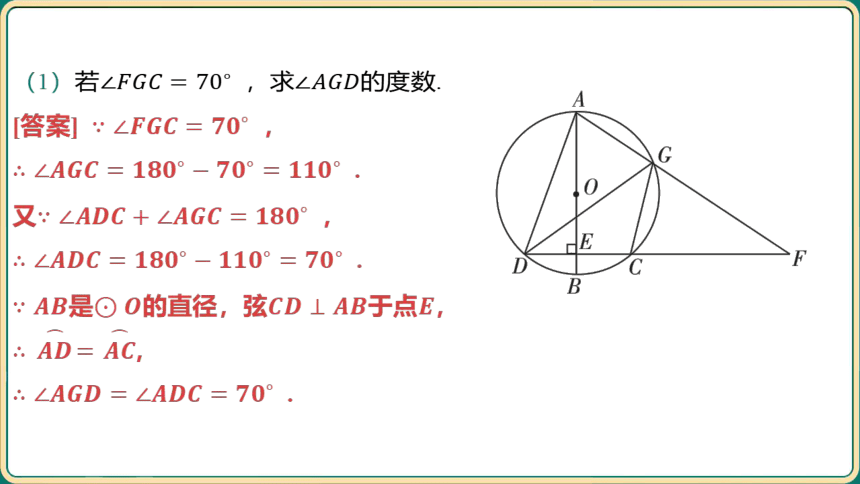
(1)若 ,求 的度数.
[答案] ,
.
又 ,
.
是的直径,弦于点 ,
,
.
(2)若点是 的中点.
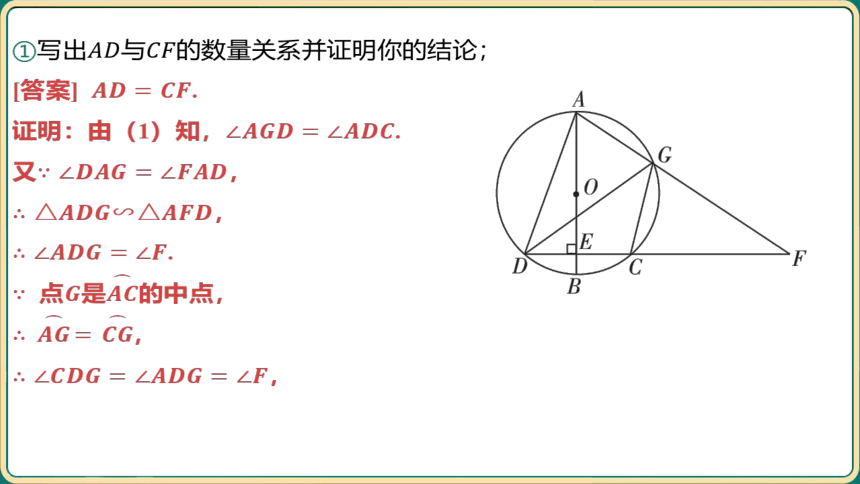
①写出与 的数量关系并证明你的结论;
[答案] .
证明:由(1)知, .
又 ,
,
.
点是 的中点,
,
,
.
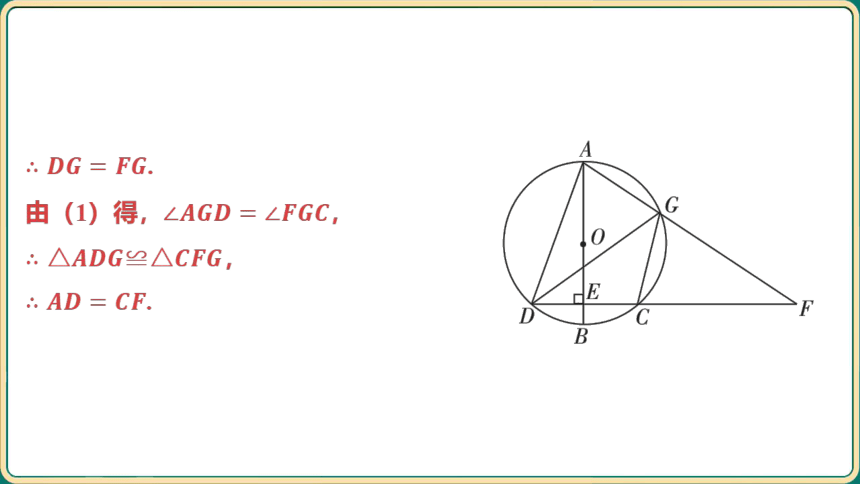
由(1)得, ,
,
.
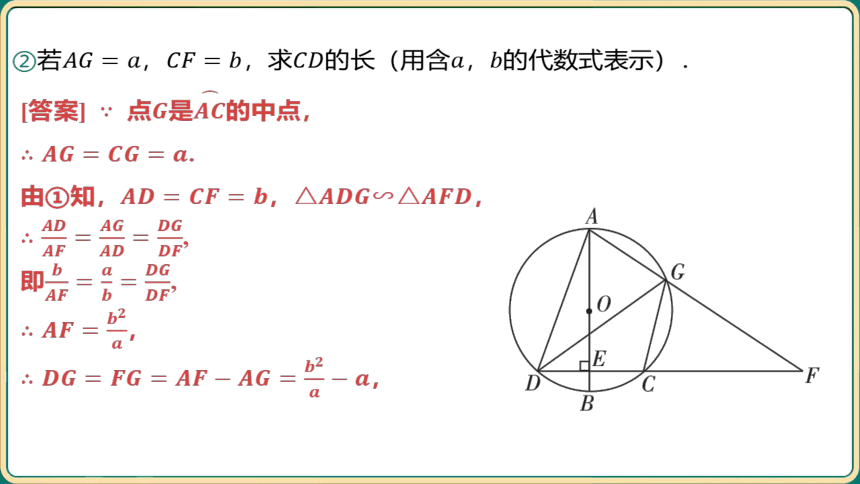
②若,,求的长(用含, 的代数式表示).
[答案] 点是 的中点,
.
由①知,, ,
,
即 ,
,
,
,
,
.
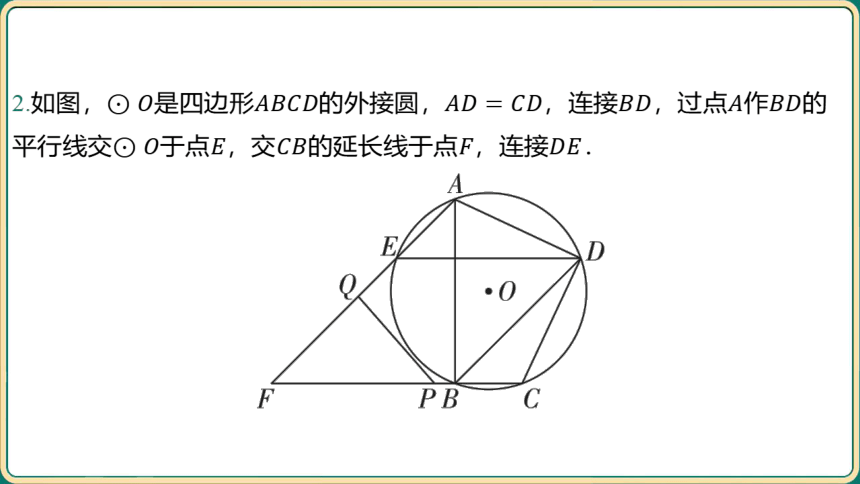
2.如图,是四边形的外接圆,,连接,过点作 的
平行线交于点,交的延长线于点,连接 .
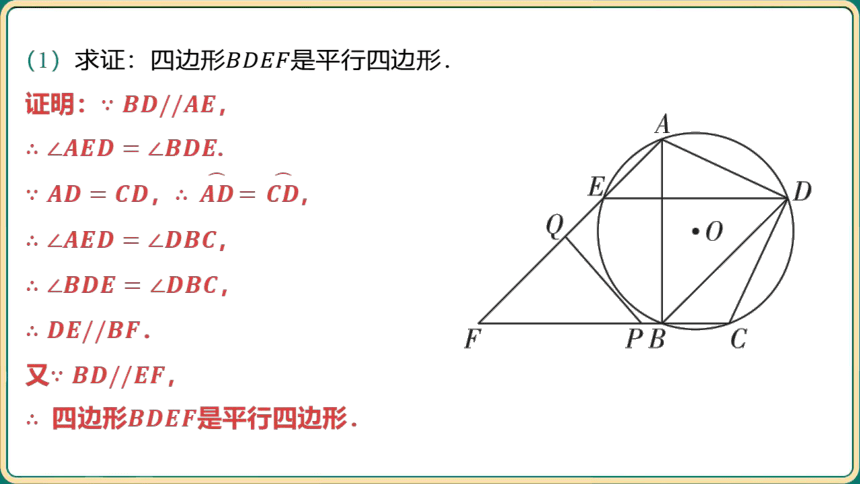
(1)求证:四边形 是平行四边形.
证明: ,
.
, ,
,
,
.
又 ,
四边形 是平行四边形.
(2)已知 , .
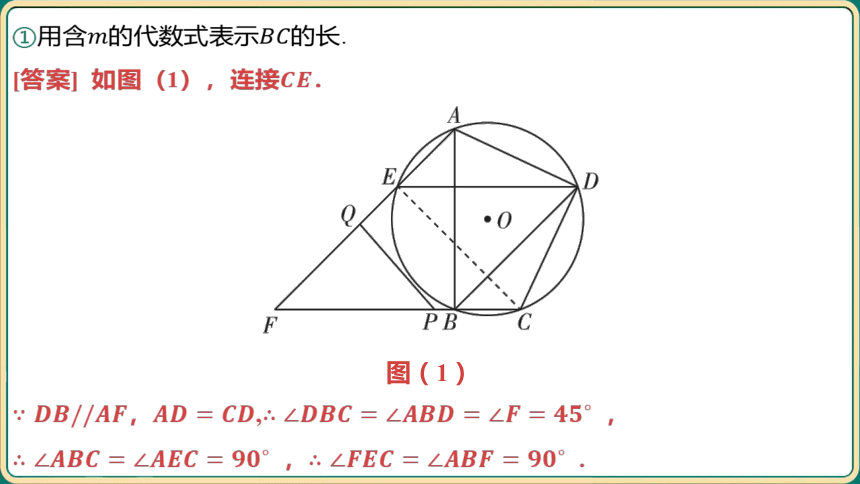
①用含的代数式表示 的长.
[答案] 如图(1),连接 .
图(1)
,, ,
, .
,
.
,
,
图(1)
②点,分别在线段,上,且.当与 相似时,
求 的值.
[答案] 四边形是平行四边形, .
又, .
令,则, .
由 可知,分以下两种情况讨论.
如图(2),当时, ,
图(2)
,
,
, ,
.
图(2)
如图(3),当时, ,
图(3)
,
.
, ,
.
综上所述,的值为 或4.
图(3)
3.如图,为的弦,点在上,平分,过点作 于
点,交于点,连接 .
(1)求 的值;
图(1)
[答案] 如图(1),过点作于点 ,
则 .
平分 ,
.
,
,
,
,
.
又 ,
四边形 为矩形,
,
.
图(1)
(2)求证: ;
[答案] 证法一:如图(1),连接 .
,
.
平分 ,
,
,
.
由(1)知,, ,
.
图(1)
证法二:如图(1),连接 .
由(1)知,四边形 为矩形,
,
.
, ,
.
又 ,
,
.
图(1)
,
,
,即 .
图(1)
(3)当时,判断 的形状,并说明理由.
[答案] 是等腰三角形.理由如下:
由(1)可知 .
又 ,
.
,
,
.
图(2)
如图(2),过点分别作,的垂线,垂足分别为, .
图(2)
设,则 ,
,
,
.
, ,
.
又 ,
,
,即 ,
,
.
图(2)
, ,
.
又 , ,
,
.
在中, ,
,
是等腰三角形.
图(2)
4.如图,在以线段为直径的上取一点,连接,,将 沿
翻折后得到 .
(1)试说明点在 上;
[答案] 如图,连接 ,
是 的直径,
.
由折叠的性质,得 .
又 ,
,
为 的半径,
即点在 上.
(2)在线段的延长线上取一点,使,求证:为 的
切线;
证明:由折叠的性质,可得 .
又 ,
,即 .
又 ,
,
,即 .
又是 的半径,
为 的切线.
(3)在(2)的条件下,分别延长线段,相交于点,若 ,
,求线段 的长.
[答案] 在中, ,, ,
.
由折叠的性质,可得 .
由(2)得,即 ,
,
.
, ,
,
.
设,,则, ,
,
, ,
.
5.如图,在的边上取一点,以为圆心,长为半径画 ,
与边相切于点,,连接交于点,连接 ,并延长
交线段于点 .
(1)求证:是 的切线;
证明:如图, 连接 ,
与边相切于点 ,
,即 .
在和中,
,
.
又是 的半径,
是 的切线.
(2)若,,求 的半径长;
[答案] 在中,, ,
, ,
.
在中, ,
,
解得 ,
的半径长为 .
(3)在(2)的条件下,若是的中点,求 的值.
[答案] 由(1)易得, .
是的中点, ,
,
.
,, .
,
,
,即 ,
,
.
6.如图,在中,是锐角,,,在射线 上取一
点,过点作于点,过,,三点作 .
(1)当 时,
①如图(1),若与相切于点,连接,求 的长;
图(1)
[答案] ,即 ,点,,在 上,
是 的直径.
与相切于点 ,
.
, ,
,
根据勾股定理,得 .
图(1)
②如图(2),若经过点,求 的半径长.
图(2)
[答案] 如图(1),连接, .
图(1)
,
是的直径, .
四边形 是平行四边形,
,,, ,
, , ,
,
.
根据勾股定理,得 ,
.
的半径长为 .
图(1)
(2)如图(3),已知与射线交于另一点,将沿 所在的直
线翻折,点的对应点记为,且恰好同时落在和边上,求此时
的长.
图(3)
图(2)
[答案] 如图(2),过点作 交
的延长线于点,连接, ,记
与的交点为 .
由折叠知,, .
,
.
,
.
,
是 的直径,
,
,
.
,
.
,
,
.
为平行四边形 边上的高,
图(2)
.
又 ,
.
设,则, .
,
.
根据勾股定理,得,即 ,
解得 ,
.
图(2)
几何压轴题专项突破
中考压轴题专项突破
圆综合题
2025年中考数学一轮复习
1.如图,已知是的直径,弦于点,是上的一点, ,
的延长线交于点,连接,, .
(1)若 ,求 的度数.
[答案] ,
.
又 ,
.
是的直径,弦于点 ,
,
.
(2)若点是 的中点.
①写出与 的数量关系并证明你的结论;
[答案] .
证明:由(1)知, .
又 ,
,
.
点是 的中点,
,
,
.
由(1)得, ,
,
.
②若,,求的长(用含, 的代数式表示).
[答案] 点是 的中点,
.
由①知,, ,
,
即 ,
,
,
,
,
.
2.如图,是四边形的外接圆,,连接,过点作 的
平行线交于点,交的延长线于点,连接 .
(1)求证:四边形 是平行四边形.
证明: ,
.
, ,
,
,
.
又 ,
四边形 是平行四边形.
(2)已知 , .
①用含的代数式表示 的长.
[答案] 如图(1),连接 .
图(1)
,, ,
, .
,
.
,
,
图(1)
②点,分别在线段,上,且.当与 相似时,
求 的值.
[答案] 四边形是平行四边形, .
又, .
令,则, .
由 可知,分以下两种情况讨论.
如图(2),当时, ,
图(2)
,
,
, ,
.
图(2)
如图(3),当时, ,
图(3)
,
.
, ,
.
综上所述,的值为 或4.
图(3)
3.如图,为的弦,点在上,平分,过点作 于
点,交于点,连接 .
(1)求 的值;
图(1)
[答案] 如图(1),过点作于点 ,
则 .
平分 ,
.
,
,
,
,
.
又 ,
四边形 为矩形,
,
.
图(1)
(2)求证: ;
[答案] 证法一:如图(1),连接 .
,
.
平分 ,
,
,
.
由(1)知,, ,
.
图(1)
证法二:如图(1),连接 .
由(1)知,四边形 为矩形,
,
.
, ,
.
又 ,
,
.
图(1)
,
,
,即 .
图(1)
(3)当时,判断 的形状,并说明理由.
[答案] 是等腰三角形.理由如下:
由(1)可知 .
又 ,
.
,
,
.
图(2)
如图(2),过点分别作,的垂线,垂足分别为, .
图(2)
设,则 ,
,
,
.
, ,
.
又 ,
,
,即 ,
,
.
图(2)
, ,
.
又 , ,
,
.
在中, ,
,
是等腰三角形.
图(2)
4.如图,在以线段为直径的上取一点,连接,,将 沿
翻折后得到 .
(1)试说明点在 上;
[答案] 如图,连接 ,
是 的直径,
.
由折叠的性质,得 .
又 ,
,
为 的半径,
即点在 上.
(2)在线段的延长线上取一点,使,求证:为 的
切线;
证明:由折叠的性质,可得 .
又 ,
,即 .
又 ,
,
,即 .
又是 的半径,
为 的切线.
(3)在(2)的条件下,分别延长线段,相交于点,若 ,
,求线段 的长.
[答案] 在中, ,, ,
.
由折叠的性质,可得 .
由(2)得,即 ,
,
.
, ,
,
.
设,,则, ,
,
, ,
.
5.如图,在的边上取一点,以为圆心,长为半径画 ,
与边相切于点,,连接交于点,连接 ,并延长
交线段于点 .
(1)求证:是 的切线;
证明:如图, 连接 ,
与边相切于点 ,
,即 .
在和中,
,
.
又是 的半径,
是 的切线.
(2)若,,求 的半径长;
[答案] 在中,, ,
, ,
.
在中, ,
,
解得 ,
的半径长为 .
(3)在(2)的条件下,若是的中点,求 的值.
[答案] 由(1)易得, .
是的中点, ,
,
.
,, .
,
,
,即 ,
,
.
6.如图,在中,是锐角,,,在射线 上取一
点,过点作于点,过,,三点作 .
(1)当 时,
①如图(1),若与相切于点,连接,求 的长;
图(1)
[答案] ,即 ,点,,在 上,
是 的直径.
与相切于点 ,
.
, ,
,
根据勾股定理,得 .
图(1)
②如图(2),若经过点,求 的半径长.
图(2)
[答案] 如图(1),连接, .
图(1)
,
是的直径, .
四边形 是平行四边形,
,,, ,
, , ,
,
.
根据勾股定理,得 ,
.
的半径长为 .
图(1)
(2)如图(3),已知与射线交于另一点,将沿 所在的直
线翻折,点的对应点记为,且恰好同时落在和边上,求此时
的长.
图(3)
图(2)
[答案] 如图(2),过点作 交
的延长线于点,连接, ,记
与的交点为 .
由折叠知,, .
,
.
,
.
,
是 的直径,
,
,
.
,
.
,
,
.
为平行四边形 边上的高,
图(2)
.
又 ,
.
设,则, .
,
.
根据勾股定理,得,即 ,
解得 ,
.
图(2)
同课章节目录
