2025年中考数学专项复习-几何压轴题专项突破18 图形变换问题 课件(共78张PPT)
文档属性
| 名称 | 2025年中考数学专项复习-几何压轴题专项突破18 图形变换问题 课件(共78张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 13:48:17 | ||
图片预览



文档简介
(共78张PPT)
几何压轴题专项突破
中考压轴题专项突破
图形变换问题
2025年中考数学一轮复习
类型1 平移
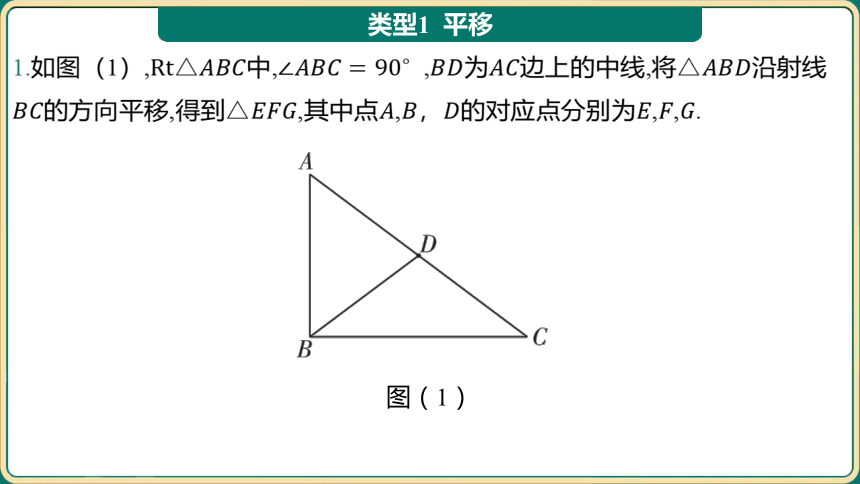
1.如图(1),中, ,为边上的中线,将 沿射线
的方向平移,得到,其中点,,的对应点分别为,, .
图(1)
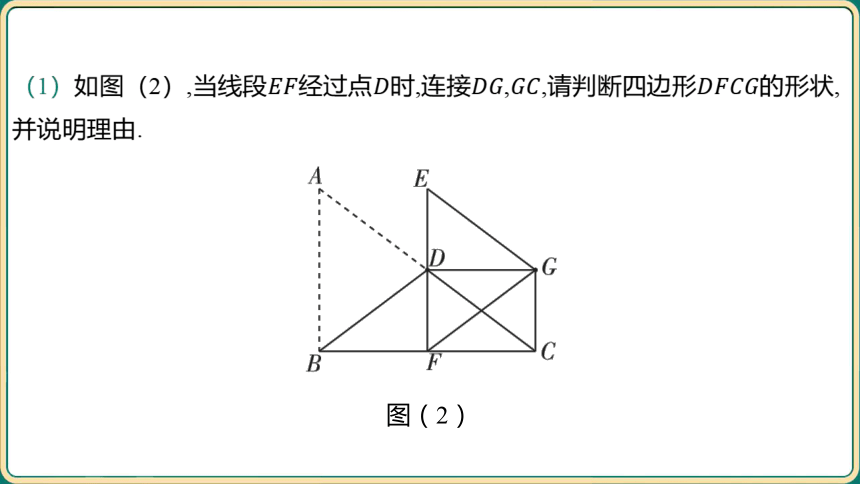
(1)如图(2),当线段经过点时,连接,,请判断四边形 的形状,
并说明理由.
图(2)
[答案] 四边形 是矩形.
理由如下: 平移得到 ,
,, ,
.
是中 边上的中线,
,
,
.
,
四边形 是平行四边形.
,
四边形 是矩形.
图(2)
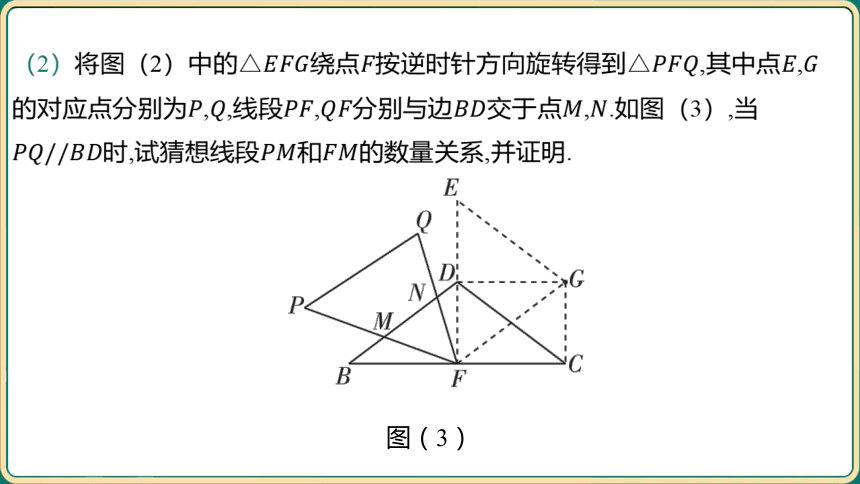
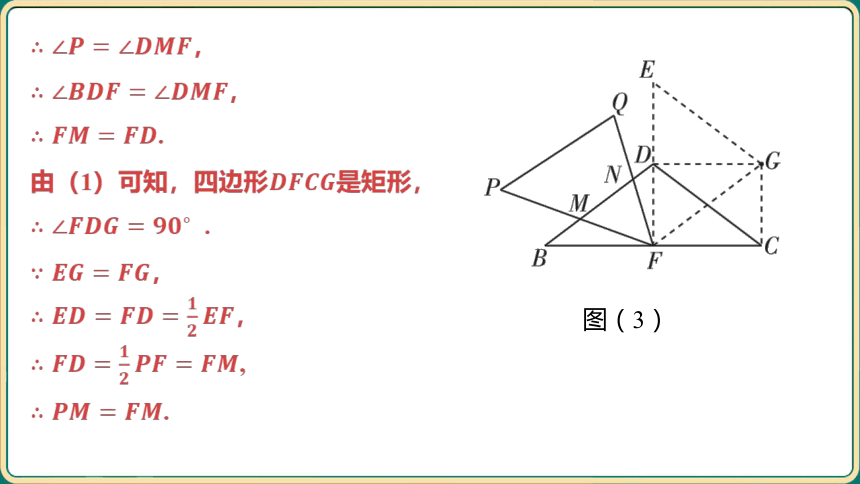
(2)将图(2)中的绕点按逆时针方向旋转得到,其中点,
的对应点分别为,,线段,分别与边交于点, .如图(3),当
时,试猜想线段和 的数量关系,并证明.
图(3)
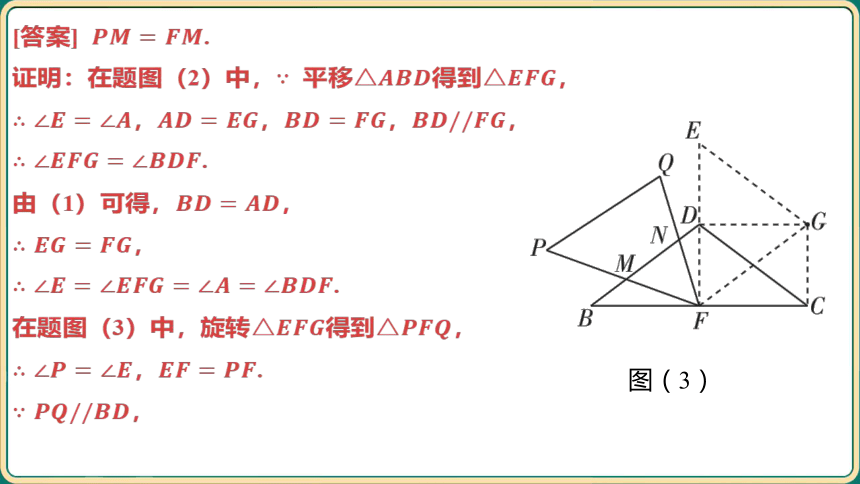
[答案] .
证明:在题图(2)中, 平移得到 ,
,,, ,
.
由(1)可得, ,
,
.
在题图(3)中,旋转得到 ,
, .
,
图(3)
,
,
.
由(1)可知,四边形 是矩形,
.
,
,
,
.
图(3)
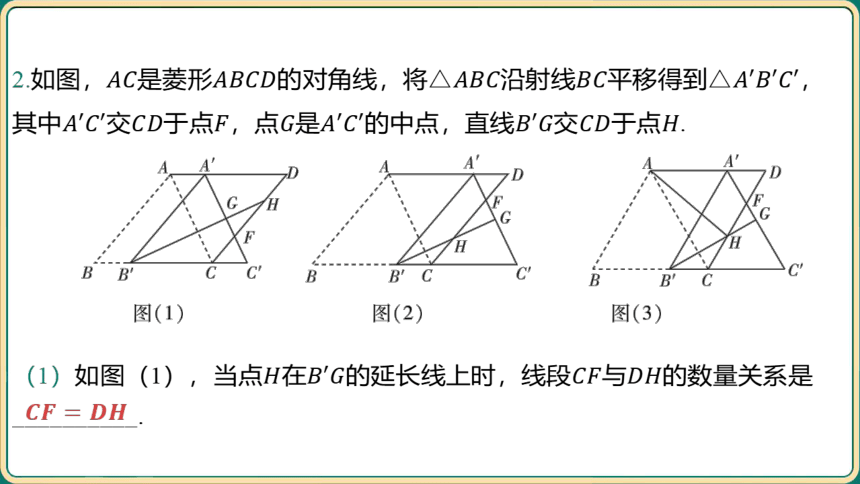
2.如图,是菱形的对角线,将沿射线平移得到 ,
其中交于点,点是的中点,直线交于点 .
(1)如图(1),当点在的延长线上时,线段与 的数量关系是
__________.
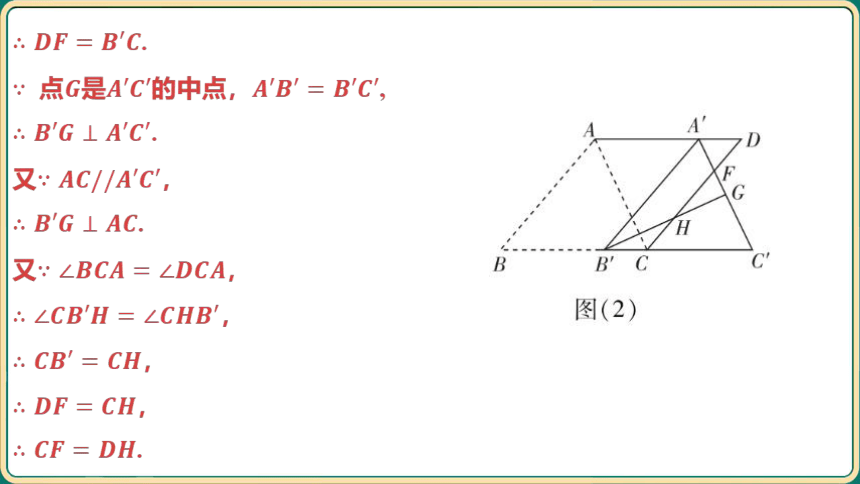
(2)如图(2),当点在线段上时,(1)中线段与 的数量关系
是否仍然成立?若成立,请加以证明;若不成立,请说明理由.
[答案] 成立.
证明: 四边形 是菱形,
,,, ,
.
由平移得,,, ,
,, ,
,四边形 是平行四边形,
, ,
.
点是的中点, ,
.
又 ,
.
又 ,
,
,
,
.
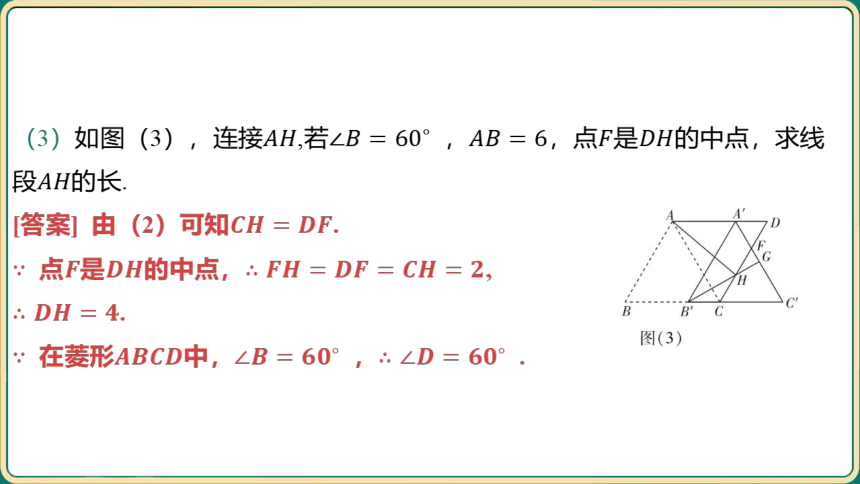
(3)如图(3),连接,若 ,,点是 的中点,求线
段 的长.
[答案] 由(2)可知 .
点是的中点, ,
.
在菱形中, , .
过点作于点 ,如图,则
, ,
,
.
类型2 对称
3.如图,在矩形纸片中,点是边上一动点,连接,将 沿
折叠得到 ,并展开铺平.
(1)在图中,过点作,垂足为点,交于点 ;(要求:尺规作
图,保留痕迹,不写作法)
[答案] 如图(1)所示.
图(1)
(2)在(1)所作的图形中连接,猜想并证明与 之间的关系.
[答案] , .
证明:如图(2).
图(2)
四边形是矩形, .
由折叠知, , ,
.
,
, ,
,
.
又 ,
,
图(2)
,
.
又 ,
四边形 是平行四边形,
, .
图(2)
4.[2024三明质检] 在中,点在上,将沿翻折得到 .
(1)如图(1),的延长线与的交点为点.求证: .
图(1)
证明: 四边形 是平行四边形,
,
.
由折叠可得 ,
,
.
图(1)
(2)如图(2),的延长线恰好经过点,若为的中点.求证: .
图(2)
[答案] 证法一:由(1)可得 .
由折叠可得, .
为 的中点,
,
,
,
,
,
.
图(2)
图(1)
证法二:如图(1),连接,交于点 .
沿翻折得到 ,
, .
垂直平分 ,
为 的中点.
为 的中点,
.
四边形 是平行四边形,
.
由(1)可得 ,
,
,
为 的中点.
是 的中位线,
.
图(1)
(3)如图(3),交于点,若, ,.求 的长.
图(3)
[答案] 如图(2),连接, .
图(2)
四边形是平行四边形, ,
是菱形,
, .
,
是等边三角形, ,
, .
沿翻折得到 ,
,, ,
, ,
,
,
即 ,
.
图(2)
过点作,交延长线于点,则 .
, .
在中, ,
.
整理,得 ,
解得 .
图(2)
5.综合与实践课上,伍老师带领学生们分小组进行折叠矩形纸片的探究活动.
【折叠实践】
第一步:如图(1),将矩形纸片对折,使边, 重合,再展开,
折痕与交于点 .
第二步:如图(2),在上取一点,沿折叠矩形,点 的对应点
为,延长交于点,将纸片沿过点的直线折叠,使点 的对应点落
在上,折痕与交于点 .
图(1)
图(2)
【初步发现】
(1)图(2)中和 的位置关系为_________.
[解析] 解法提示:, .
由折叠的性质,得, ,
, .
【深入探究】
(2)勤学小组的同学们选用了如图(3)所示的矩形纸片,选取的点 与点
重合,按步骤折叠后发现,点,,共线.请你帮他们求出 的值.
图(3)
图(1)
[答案] 设, .
如图(1),连接 ,
在和 中,
,, ,
, .
又, .
由(1)得, ,
, ,
,
.
在中, ,
,
,, .
图(1)
【拓展延伸】
(3)奋进小组的同学们选用了, 的矩形纸片,按步骤
进行多次折叠(选取不同位置的点),且第二步折叠中,折痕与 交于点
,把纸片展开后,连接 (图(4)是奋进小组的一次折叠样例).请你解
决:当为直角三角形时,直接写出 的长.
图(4)
[答案] 的长为或 .
图(2)
[解析] 解法提示:分两种情况讨论.
①当 时,如图(2),此时 .
又 , ,
四边形是正方形, .
图(3)
②当 时,如图(3),过点作 于
点 ,
则 .
在和 中,
,, ,
, .
又, ,
.
易证 ,
,即 ,
.
综上可知,的长为或 .
类型3 旋转
6.如图,已知和 都是等腰直角三角
形, ,, .将
绕点旋转,使得点落在 内部,连接
, .
(1)求证: ;
证明:和都是等腰直角三角形, ,
,
,即 ,
,即 ,
.
(2)当时,求 的值.
[答案] 如图,
当时, ,
又 ,
.
由(1)得 ,
,
,
即,, 三点共线.
在中, ,
, ,
,
.
7.[2024成都中考节选] 数学活动课上,同学们将两个全等的三角形纸片完全
重合放置,固定一个顶点,然后将其中一个纸片绕这个顶点旋转,来探究图形旋
转的性质.已知三角形纸片和中,, ,
.
图(1)
(1)如图(1),连接,,在纸片绕点
旋转的过程中,试探究 的值;
[答案] 由勾股定理,得
.
由旋转的性质,得 .
又 ,
, .
(2)如图(2),在纸片绕点旋转的过程中,当点恰好落在 的中
线的延长线上时,延长交于点,求 的长.
图(2)
[答案] 如图,连接,延长交于点,延长 交
于点,连接交于点 .
点为的中点, ,
, .
由旋转可知,, ,
,
,
.
,, ,
,
,
四边形 是平行四边形.
又 , 四边形 是矩形,
,, ,
,
,
.
连接 .
,, ,
, .
设,则, ,
.
由勾股定理,得 ,
,解得 ,
, ,
.
, ,
,
.
8.如图,在中,,将绕点逆时针旋转 度 得
到,与交于点,连接,, .
(1)如图(1),求证: ;
证明:设,的交点为 .
, .
又 ,
.
(2)如图(2),若 ,求证:四边形 是菱形;
证明:, .
又由(1)得 , ,
.
同理可得, 四边形 是平行四边形.
又, 四边形 是菱形.
(3)如图(3),若,且,求 的值.
[答案] , ,
又, ,
,, .
过点作于点,则 ,
.
方法一:, .
如图(1),过点作于点 ,
图(1)
则 .
设,则,, ,
.
方法二:如图(2),延长交的延长线于点 .
图(2)
设,则, .
,
, ,
, ,
,
.
图(2)
9.[2023福州质检] 如图(1),在中, ,, ,将
绕点顺时针旋转得到,其中点是点 的对应点,且
,连接, .
(1)求证: ;
证明:在中, ,, ,
.
绕点顺时针旋转得到 ,
,, ,
,, .
(2)如图(2),当点在线段上时,求 的面积;
[答案] 如图(1),过点作的垂线,垂足为 ,
图(1)
.
记 ,则, .
由(1)可得, ,
,
, .
,
, .
图(1)
(3)直线与直线交于点,是边的中点,连接 ,在旋转过程中,求
的最大值.
[答案] 由(2)得 .
当点,在 异侧时,如图(2),
图(2)
,
.
在四边形中, ,
,
.
图(2)
当点,在 同侧时,如图(3),
图(3)
,
,
即 ,
,
.
取中点,连接, ,
.
为的中点,为 的中位线,
,
,
即 的最大值为4.
图(3)
10.如图(1),正方形 与正方形
有公共点,点, 分别在
,上,点在正方形 的对
角线上.将正方形绕 点按逆
时针方向旋转,旋转角为
.
(1)如图(1),当 时, ____;
[解析] 解法提示: 四边形是正方形,四边形 是正方形,
, ,
,, .
(2)如图(2),当 时,连接,,求 的值;
[答案] 如图(1),连接 ,
图(1)
由旋转知 .
在和 中,
, ,
, ,
, .
图(1)
(3)若,,当,,三点共线时,求 的长度.
[答案] 同(2)可证 .
四边形 是正方形,
, .
四边形 是正方形,
, .
,,三点共线, .
分两种情况讨论:
①当点在线段的延长线上时,如图(2),连接 .
图(2)
,
.
②当点在线段上时,如图(3),连接 .
图(3)
, .
综上,当,,三点共线时,的长度为或 .
11.在中, .将绕点顺时针旋转得到 ,旋转
角小于,点的对应点为点,点的对应点为点,交于点 ,
延长交于点 .
(1)如图(1),求证: .
证明:如图(1),连接 .
图(1)
将绕点顺时针旋转得到 ,由旋转的性质可得
, ,
, ,
,即 ,
.
图(1)
(2)当 时,
①如图(2),若,,求线段 的长;
[答案] 在中, ,, ,
.
,
, .
由旋转的性质可得 ,
,
,, .
由旋转的性质可得 ,
.
由(1)知, .
②如图(3),连接,,延长交于点,判断是否为线段 的
中点,并说明理由.
图(2)
[答案] 是线段 的中点.
理由如下:如图(2),延长, 相交于点 .
, .
, ,
, .
由旋转的性质可得, .
又, ,
,即是线段 的中点.
12.已知矩形,,,把矩形绕点 顺时针旋转,得到矩形
,连接,交于点 .
(1)如图(1),若点落在边上,过点作,垂足为点,连接 ,求
证: .
证明: ,
.
四边形 是矩形,
, , ,
,
.
, ,
,
.
,
.
在与 中,
.
(2)如图(2),若点在上方,连接交于点,连接,若 ,
①求证: ;
证明:如图,过点作,垂足为点 .
四边形是矩形, ,
, ,
.
,
, .
, .
, ,
,, ,
(舍去), .
, ,
,
, .
, ,
可设,则 .
在中, ,
,
解得, (舍去).
,
.
②求 的长.
[答案] , ,
.
,
,
.
,, ,
.
几何压轴题专项突破
中考压轴题专项突破
图形变换问题
2025年中考数学一轮复习
类型1 平移
1.如图(1),中, ,为边上的中线,将 沿射线
的方向平移,得到,其中点,,的对应点分别为,, .
图(1)
(1)如图(2),当线段经过点时,连接,,请判断四边形 的形状,
并说明理由.
图(2)
[答案] 四边形 是矩形.
理由如下: 平移得到 ,
,, ,
.
是中 边上的中线,
,
,
.
,
四边形 是平行四边形.
,
四边形 是矩形.
图(2)
(2)将图(2)中的绕点按逆时针方向旋转得到,其中点,
的对应点分别为,,线段,分别与边交于点, .如图(3),当
时,试猜想线段和 的数量关系,并证明.
图(3)
[答案] .
证明:在题图(2)中, 平移得到 ,
,,, ,
.
由(1)可得, ,
,
.
在题图(3)中,旋转得到 ,
, .
,
图(3)
,
,
.
由(1)可知,四边形 是矩形,
.
,
,
,
.
图(3)
2.如图,是菱形的对角线,将沿射线平移得到 ,
其中交于点,点是的中点,直线交于点 .
(1)如图(1),当点在的延长线上时,线段与 的数量关系是
__________.
(2)如图(2),当点在线段上时,(1)中线段与 的数量关系
是否仍然成立?若成立,请加以证明;若不成立,请说明理由.
[答案] 成立.
证明: 四边形 是菱形,
,,, ,
.
由平移得,,, ,
,, ,
,四边形 是平行四边形,
, ,
.
点是的中点, ,
.
又 ,
.
又 ,
,
,
,
.
(3)如图(3),连接,若 ,,点是 的中点,求线
段 的长.
[答案] 由(2)可知 .
点是的中点, ,
.
在菱形中, , .
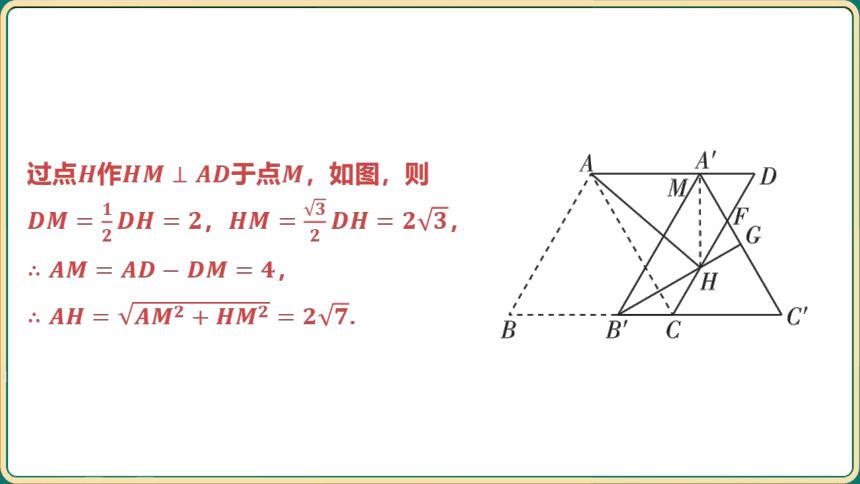
过点作于点 ,如图,则
, ,
,
.
类型2 对称
3.如图,在矩形纸片中,点是边上一动点,连接,将 沿
折叠得到 ,并展开铺平.
(1)在图中,过点作,垂足为点,交于点 ;(要求:尺规作
图,保留痕迹,不写作法)
[答案] 如图(1)所示.
图(1)
(2)在(1)所作的图形中连接,猜想并证明与 之间的关系.
[答案] , .
证明:如图(2).
图(2)
四边形是矩形, .
由折叠知, , ,
.
,
, ,
,
.
又 ,
,
图(2)
,
.
又 ,
四边形 是平行四边形,
, .
图(2)
4.[2024三明质检] 在中,点在上,将沿翻折得到 .
(1)如图(1),的延长线与的交点为点.求证: .
图(1)
证明: 四边形 是平行四边形,
,
.
由折叠可得 ,
,
.
图(1)
(2)如图(2),的延长线恰好经过点,若为的中点.求证: .
图(2)
[答案] 证法一:由(1)可得 .
由折叠可得, .
为 的中点,
,
,
,
,
,
.
图(2)
图(1)
证法二:如图(1),连接,交于点 .
沿翻折得到 ,
, .
垂直平分 ,
为 的中点.
为 的中点,
.
四边形 是平行四边形,
.
由(1)可得 ,
,
,
为 的中点.
是 的中位线,
.
图(1)
(3)如图(3),交于点,若, ,.求 的长.
图(3)
[答案] 如图(2),连接, .
图(2)
四边形是平行四边形, ,
是菱形,
, .
,
是等边三角形, ,
, .
沿翻折得到 ,
,, ,
, ,
,
,
即 ,
.
图(2)
过点作,交延长线于点,则 .
, .
在中, ,
.
整理,得 ,
解得 .
图(2)
5.综合与实践课上,伍老师带领学生们分小组进行折叠矩形纸片的探究活动.
【折叠实践】
第一步:如图(1),将矩形纸片对折,使边, 重合,再展开,
折痕与交于点 .
第二步:如图(2),在上取一点,沿折叠矩形,点 的对应点
为,延长交于点,将纸片沿过点的直线折叠,使点 的对应点落
在上,折痕与交于点 .
图(1)
图(2)
【初步发现】
(1)图(2)中和 的位置关系为_________.
[解析] 解法提示:, .
由折叠的性质,得, ,
, .
【深入探究】
(2)勤学小组的同学们选用了如图(3)所示的矩形纸片,选取的点 与点
重合,按步骤折叠后发现,点,,共线.请你帮他们求出 的值.
图(3)
图(1)
[答案] 设, .
如图(1),连接 ,
在和 中,
,, ,
, .
又, .
由(1)得, ,
, ,
,
.
在中, ,
,
,, .
图(1)
【拓展延伸】
(3)奋进小组的同学们选用了, 的矩形纸片,按步骤
进行多次折叠(选取不同位置的点),且第二步折叠中,折痕与 交于点
,把纸片展开后,连接 (图(4)是奋进小组的一次折叠样例).请你解
决:当为直角三角形时,直接写出 的长.
图(4)
[答案] 的长为或 .
图(2)
[解析] 解法提示:分两种情况讨论.
①当 时,如图(2),此时 .
又 , ,
四边形是正方形, .
图(3)
②当 时,如图(3),过点作 于
点 ,
则 .
在和 中,
,, ,
, .
又, ,
.
易证 ,
,即 ,
.
综上可知,的长为或 .
类型3 旋转
6.如图,已知和 都是等腰直角三角
形, ,, .将
绕点旋转,使得点落在 内部,连接
, .
(1)求证: ;
证明:和都是等腰直角三角形, ,
,
,即 ,
,即 ,
.
(2)当时,求 的值.
[答案] 如图,
当时, ,
又 ,
.
由(1)得 ,
,
,
即,, 三点共线.
在中, ,
, ,
,
.
7.[2024成都中考节选] 数学活动课上,同学们将两个全等的三角形纸片完全
重合放置,固定一个顶点,然后将其中一个纸片绕这个顶点旋转,来探究图形旋
转的性质.已知三角形纸片和中,, ,
.
图(1)
(1)如图(1),连接,,在纸片绕点
旋转的过程中,试探究 的值;
[答案] 由勾股定理,得
.
由旋转的性质,得 .
又 ,
, .
(2)如图(2),在纸片绕点旋转的过程中,当点恰好落在 的中
线的延长线上时,延长交于点,求 的长.
图(2)
[答案] 如图,连接,延长交于点,延长 交
于点,连接交于点 .
点为的中点, ,
, .
由旋转可知,, ,
,
,
.
,, ,
,
,
四边形 是平行四边形.
又 , 四边形 是矩形,
,, ,
,
,
.
连接 .
,, ,
, .
设,则, ,
.
由勾股定理,得 ,
,解得 ,
, ,
.
, ,
,
.
8.如图,在中,,将绕点逆时针旋转 度 得
到,与交于点,连接,, .
(1)如图(1),求证: ;
证明:设,的交点为 .
, .
又 ,
.
(2)如图(2),若 ,求证:四边形 是菱形;
证明:, .
又由(1)得 , ,
.
同理可得, 四边形 是平行四边形.
又, 四边形 是菱形.
(3)如图(3),若,且,求 的值.
[答案] , ,
又, ,
,, .
过点作于点,则 ,
.
方法一:, .
如图(1),过点作于点 ,
图(1)
则 .
设,则,, ,
.
方法二:如图(2),延长交的延长线于点 .
图(2)
设,则, .
,
, ,
, ,
,
.
图(2)
9.[2023福州质检] 如图(1),在中, ,, ,将
绕点顺时针旋转得到,其中点是点 的对应点,且
,连接, .
(1)求证: ;
证明:在中, ,, ,
.
绕点顺时针旋转得到 ,
,, ,
,, .
(2)如图(2),当点在线段上时,求 的面积;
[答案] 如图(1),过点作的垂线,垂足为 ,
图(1)
.
记 ,则, .
由(1)可得, ,
,
, .
,
, .
图(1)
(3)直线与直线交于点,是边的中点,连接 ,在旋转过程中,求
的最大值.
[答案] 由(2)得 .
当点,在 异侧时,如图(2),
图(2)
,
.
在四边形中, ,
,
.
图(2)
当点,在 同侧时,如图(3),
图(3)
,
,
即 ,
,
.
取中点,连接, ,
.
为的中点,为 的中位线,
,
,
即 的最大值为4.
图(3)
10.如图(1),正方形 与正方形
有公共点,点, 分别在
,上,点在正方形 的对
角线上.将正方形绕 点按逆
时针方向旋转,旋转角为
.
(1)如图(1),当 时, ____;
[解析] 解法提示: 四边形是正方形,四边形 是正方形,
, ,
,, .
(2)如图(2),当 时,连接,,求 的值;
[答案] 如图(1),连接 ,
图(1)
由旋转知 .
在和 中,
, ,
, ,
, .
图(1)
(3)若,,当,,三点共线时,求 的长度.
[答案] 同(2)可证 .
四边形 是正方形,
, .
四边形 是正方形,
, .
,,三点共线, .
分两种情况讨论:
①当点在线段的延长线上时,如图(2),连接 .
图(2)
,
.
②当点在线段上时,如图(3),连接 .
图(3)
, .
综上,当,,三点共线时,的长度为或 .
11.在中, .将绕点顺时针旋转得到 ,旋转
角小于,点的对应点为点,点的对应点为点,交于点 ,
延长交于点 .
(1)如图(1),求证: .
证明:如图(1),连接 .
图(1)
将绕点顺时针旋转得到 ,由旋转的性质可得
, ,
, ,
,即 ,
.
图(1)
(2)当 时,
①如图(2),若,,求线段 的长;
[答案] 在中, ,, ,
.
,
, .
由旋转的性质可得 ,
,
,, .
由旋转的性质可得 ,
.
由(1)知, .
②如图(3),连接,,延长交于点,判断是否为线段 的
中点,并说明理由.
图(2)
[答案] 是线段 的中点.
理由如下:如图(2),延长, 相交于点 .
, .
, ,
, .
由旋转的性质可得, .
又, ,
,即是线段 的中点.
12.已知矩形,,,把矩形绕点 顺时针旋转,得到矩形
,连接,交于点 .
(1)如图(1),若点落在边上,过点作,垂足为点,连接 ,求
证: .
证明: ,
.
四边形 是矩形,
, , ,
,
.
, ,
,
.
,
.
在与 中,
.
(2)如图(2),若点在上方,连接交于点,连接,若 ,
①求证: ;
证明:如图,过点作,垂足为点 .
四边形是矩形, ,
, ,
.
,
, .
, .
, ,
,, ,
(舍去), .
, ,
,
, .
, ,
可设,则 .
在中, ,
,
解得, (舍去).
,
.
②求 的长.
[答案] , ,
.
,
,
.
,, ,
.
同课章节目录
