2025年中考数学专项复习--题型二 实际应用题 课件(共35张PPT)
文档属性
| 名称 | 2025年中考数学专项复习--题型二 实际应用题 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 13:52:21 | ||
图片预览











文档简介
(共35张PPT)
题型二 实际应用题
中考题型专项突破
2025年中考数学一轮复习
类型1 利用方程(组)、不等式解决实际问题
1.小张周末到艺术公园参加销售文创产品的社会实践活动,销售A产品5个,B
产品5个,销售金额为125元;销售A产品2个,B产品5个,销售金额为80元.
(1)求A,B两种文创产品的销售单价分别是多少元.
[答案] 设A产品的销售单价是元,B产品的销售单价是 元,
根据题意,得解得
答:A产品的销售单价是15元,B产品的销售单价是10元.
(2)若A产品进价12元,B产品进价8元,小张用不超过980元购进两种产品
共100件,准备用销售这批产品的利润购买250元课外科普读物,请问小张的
目标能实现吗?若能,请给出相应的进货方案;若不能,请说明理由.
[答案] 小张的目标不能实现,理由如下:
设购进个A产品,则购进 个B产品.
根据题意,得,解得 .
若销售这批产品的利润为250元,
则,解得 ,
,即A产品最多只能购进45件,
小张的目标不能实现.
2.为充分发挥科技生产力对企业和产业发展的作
用,某镇计划引进无人机田间喷洒农药技术.无
人机喷洒农药时,平均每亩地用药量比常规喷药
壶用药量少,无人机用药 喷洒的农
田面积与常规喷药壶用药喷洒的农田面积相同.(注:1亩 )
(1)求无人机喷洒农药时,平均每亩地的用药量.
[答案] 设无人机喷洒农药时,平均每亩地的用药量为 .
根据题意,列方程为 ,
解得 .
经检验, 是原分式方程的根,且符合实际.
答:无人机喷洒农药时,平均每亩地的用药量为 .
(2)该镇计划采购A,B两种型号喷药无人机共20台.已知A型号喷药无人机
每台15 000元,B型号喷药无人机每台20 000元,若采购资金不超过360 000
元,则最少需采购A型号喷药无人机多少台
[答案] 设采购A型号喷药无人机 台.
根据题意,得 ,
解得 .
答:最少需采购A型号喷药无人机8台.
3.【新情境】健康中国,营养先行.2024年5月12日 日是第十届全民营养周,
社区食堂在全民营养周到来之际,推出系列营养套餐,其中营养套餐A的菜品如
下图所示.
_____________________________________________________________________________________________________________________________________________________________
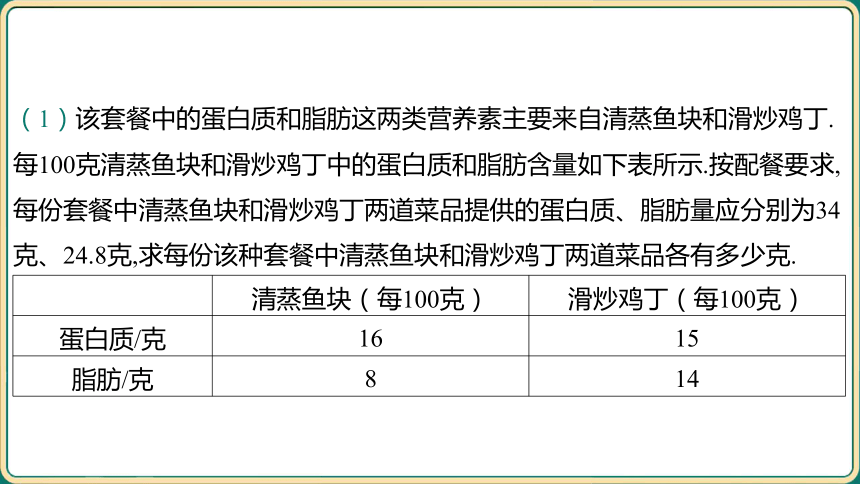
(1)该套餐中的蛋白质和脂肪这两类营养素主要来自清蒸鱼块和滑炒鸡丁.
每100克清蒸鱼块和滑炒鸡丁中的蛋白质和脂肪含量如下表所示.按配餐要求,
每份套餐中清蒸鱼块和滑炒鸡丁两道菜品提供的蛋白质、脂肪量应分别为34
克、24.8克,求每份该种套餐中清蒸鱼块和滑炒鸡丁两道菜品各有多少克.
清蒸鱼块(每100克) 滑炒鸡丁(每100克)
蛋白质/克 16 15
脂肪/克 8 14
[答案] 设每份该种套餐中清蒸鱼块有克,滑炒鸡丁有 克.
根据题意,得
解得
答:每份该种套餐中清蒸鱼块有100克,滑炒鸡丁有120克.
(2)按配餐要求,每份素炒时蔬中芹菜与西蓝花共260克,已知每100克芹菜
与每100克西蓝花分别含有1.5克、2.5克的膳食纤维.若要使每份素炒时蔬中所
含的膳食纤维不少于5克,则每份素炒时蔬中西蓝花至少有多少克
[答案] 设每份素炒时蔬中西蓝花有 克.
根据题意,得 ,
解得 ,
所以 的最小值为110.
答:每份素炒时蔬中西蓝花至少有110克.
类型2 利用函数解决实际问题
4.某学校计划一次性购买A,B两种类型的书架,用于建设班级读书角,方便
学生利用课余时间阅览图书.已知购买3个A型书架和4个B型书架共需640元,
购买5个A型书架和2个B型书架共需670元.
(1)求购买一个A型书架和一个B型书架各需多少元.
[答案] 设购买一个A型书架需要元,购买一个B型书架需要 元,
根据题意,得
解得
答:购买一个A型书架需要100元,购买一个B型书架需要85元.
(2)该学校打算购买A,B两种类型的书架共52个,且购买的总费用不超过4
700元.若A型书架的最大放书量为80册,B型书架的最大放书量为65册,请设
计出放书总量最大的购买方案,并说明理由.
[答案] 放书总量最大的购买方案为购买18个A型书架,34个B型书架.
理由:设购买个A型书架,则购买 个B型书架,
根据题意,得 ,
解得 .
设购买两种类型书架的放书总量为 册,
则 .
,随 的增大而增大.
又,且 为整数,
当时,取得最大值,此时 ,
放书总量最大的购买方案为:购买18个A型书架,34个B型书架.
5.某市为了科学处理垃圾,新建了A,B两类垃圾处理场共20个,其中A类垃
圾处理厂处理不可回收垃圾,B类垃圾处理厂处理可回收垃圾,已知每一个
A类垃圾处理场日处理量为30吨,每一个B类垃圾处理场日处理量为40吨,
该市新建的20个垃圾处理场每天处理城市垃圾总量为720吨.
(1)求该市新建的A,B两类垃圾处理场各有多少个.
[答案] 设A类垃圾处理场有个,B类垃圾处理场有 个,
根据题意,得
解得
答:A类垃圾处理场有8个,B类垃圾处理场有12个.
(2)为了环保要求,该市将不可回收垃圾再次细分为不可回收垃圾和有害
垃圾,致使A类垃圾处理场日处理量减少了5吨,市政府拟将 个B类
垃圾处理场改建成A类垃圾处理场,请给出两类垃圾处理场日处理垃圾总量
最大的改建方案,并求出日处理垃圾总量的最大值.
[答案] 若A类垃圾处理场增加个,则B类垃圾处理场为 个.
设两类垃圾处理场日处理垃圾总量为 吨,则
.
,随着 的增大而减小.
又 ,
当 时,改建后两类垃圾处理场日处理垃圾总量最大,
(吨).
答:将3个B类垃圾处理场改建成A类垃圾处理场,两类垃圾处理场日处理垃
圾总量最大,为635吨.
6.近年来,市民交通安全意识逐步增强,头盔需求量增大.某生产厂家销售甲、
乙两种头盔,已知甲种头盔比乙种头盔的单价多11元,购进甲种头盔10个,
乙种头盔20个,共需1 730元.
(1)求甲、乙两种头盔的单价.
[答案] 设甲、乙两种头盔的单价分别为元、 元.
由题意列方程组得解得
答:甲、乙两种头盔的单价分别为65元、54元.
(2)某商店欲购进两种头盔共100个,正好赶上厂家进行促销活动,促销方
式如下:甲种头盔按单价的8折出售,乙种头盔每个降价6元出售.如果此次购
买甲种头盔的数量不低于乙种头盔的数量,那么购买多少个甲种头盔可以使
此次购买头盔的总费用最少 最少费用是多少元
[答案] 设购买甲种头盔个,则购买乙种头盔 个,
根据题意,得,解得 .
设此次购买头盔的总费用为 元,
则 .
,随 的增大而增大.
当时, 有最小值,
.
答:购买50个甲种头盔可以使此次购买头盔的总费用最少,最少费用是
5 000元.
7.星期日上午 ,小明从家里出发步行
前往离家 的镇海书城参加读书会活
动,他以的速度步行了
后发现忘带入场券,于是他停下来,打电
话给家里的爸爸寻求帮助.9:15爸爸骑着自
行车从家里出发,沿着同一路线以
的速度行进,同一时刻小明继续按原速步行赶往目的地.爸爸追
上小明后载上他以相同的车速前往书城(停车载人时间忽略不计),到达书
城后爸爸原速返回家.爸爸和小明离家的路程与小明所用时间 的
函数关系如图所示.
(1)求爸爸在到达镇海书城前,他离开家的路程关于的函数表达式及 的
值.
[答案] 方法一:爸爸到达镇海书城所用时间为 ,
设爸爸在到达镇海书城前,他离开家的路程关于 的函数表达式为
,
把,分别代入 ,
得
解得
爸爸在到达镇海书城前,他离开家的路程关于 的函数表达式为
.
爸爸的速度不变,
他返回家的时间和到达书城的时间均为 ,
.
方法二:由题意知,爸爸在小明出发后出发,速度为 ,
爸爸在到达镇海书城前,他离开家的路程
.
又 爸爸的速度不变,
.
(2)爸爸出发多长时间后追上小明?此时距离镇海书城还有多远?
[答案] 设爸爸出发 后追上小明,
则 ,
解得 ,
.
答:爸爸出发后追上小明,此时距离镇海书城还有 .
8.近年来,直播带货成了一个火热的新兴职业.某主播带货图书《苏东坡传》,
他用双语直播,风趣幽默,点燃了观众的读书热情.已知这本书的进价为10元,
规定售价不低于进价,且不高于进价的3倍,通过前几天的销售发现,该书
每天的销售量(本)与售价 (元 /本)之间近似满足一次函数关系,部分
对应数据如下表所示:
(元/本) … 15 25 …
本 … 700 500 …
(1)根据表格提供的数据,求与的函数关系式,并写出 的取值范围.
[答案] 设与的函数关系式为 .
依题意,得
解得
与的函数关系式为 .
(2)若销售该书每天的利润为6 000元,求该书的售价.
[答案] 依题意,得 ,
整理,得 ,
解得, .
, .
若销售该书每天的利润为6 000元,则该书的售价为20元/本.
(3)销售该书每天的利润能否达到9 000元 请说明理由.
[答案] 不能.理由如下.
方法一:依题意,得 ,
整理,得 .
,
该方程没有实数根,
销售该书每天的利润不能达到9 000元.
方法二:设销售该书每天的利润为 元,则
.
当时,有最大值 ,即销售该书每天的最大利润为8 000元.
,
销售该书每天的利润不能达到9 000元.
9.【新考法】学科实践
驱动任务:“过水门”是国际民航中高级别的礼仪,因两辆(或以上)的消防车
在飞机两侧喷射水柱出现一个“水门”状的效果而得名(如图(1)).学校计
划在运动会开幕式上举行彩旗队“过水门”仪式,数学研习小组协助彩旗队进行
队列设计.
研究步骤:①如图(2),研习小组测得表演场地的宽度米,在, 处各
安装一个接通水源的喷泉喷头,将出水口高度, 都设为1米,调整出水速度
与角度,使喷出的两条抛物线形水柱形状相同,并在抛物线顶点 处相遇,组成
一条完整的抛物线形水门,且点 到地面的距离为5米;
②研习小组了解到彩旗队的队列设置要求,每两列之间保持相同的间距,队员
所持彩旗的顶端离地面的距离保持3.6米.
图(1)
图(2)
问题解决:请根据上述研究步骤与相关数据,完成下列任务.
(1)以线段所在直线为轴,的垂直平分线为 轴建立平面直角坐标系,
请在图中画出坐标系,并求出“过水门”仪式中水柱所在抛物线的函数表达式;
[答案] 建立如图所示的平面直角坐标系.
设所求抛物线的函数表达式为 ,
由题可知,米, ,
米, 米,
所以,点的坐标为,点的坐标为, .
将,代入 ,
得
解得
所以,所求抛物线的函数表达式为 .
(2)为保证“水门”的水柱不被破坏,要求队列最外侧的两列同学所持彩旗顶
端与水柱间的铅直距离为0.4米,若彩旗队要排成6列纵队,请你通过计算,确定
彩旗队“过水门”时,每相邻两列纵队的间距.
[答案] 如图,分别过最外侧队员彩旗顶端作 轴的
垂线,,垂足为点,,分别交抛物线于点, .
由题意可知, (米),
所以,点, 的纵坐标均为4.
当时, ,
解得 ,
点,的坐标分别为和 .
所以,最外侧两列彩旗队之间的距离为 (米).
所以, (米).
答:彩旗队每相邻两列纵队的间距为1.6米.
题型二 实际应用题
中考题型专项突破
2025年中考数学一轮复习
类型1 利用方程(组)、不等式解决实际问题
1.小张周末到艺术公园参加销售文创产品的社会实践活动,销售A产品5个,B
产品5个,销售金额为125元;销售A产品2个,B产品5个,销售金额为80元.
(1)求A,B两种文创产品的销售单价分别是多少元.
[答案] 设A产品的销售单价是元,B产品的销售单价是 元,
根据题意,得解得
答:A产品的销售单价是15元,B产品的销售单价是10元.
(2)若A产品进价12元,B产品进价8元,小张用不超过980元购进两种产品
共100件,准备用销售这批产品的利润购买250元课外科普读物,请问小张的
目标能实现吗?若能,请给出相应的进货方案;若不能,请说明理由.
[答案] 小张的目标不能实现,理由如下:
设购进个A产品,则购进 个B产品.
根据题意,得,解得 .
若销售这批产品的利润为250元,
则,解得 ,
,即A产品最多只能购进45件,
小张的目标不能实现.
2.为充分发挥科技生产力对企业和产业发展的作
用,某镇计划引进无人机田间喷洒农药技术.无
人机喷洒农药时,平均每亩地用药量比常规喷药
壶用药量少,无人机用药 喷洒的农
田面积与常规喷药壶用药喷洒的农田面积相同.(注:1亩 )
(1)求无人机喷洒农药时,平均每亩地的用药量.
[答案] 设无人机喷洒农药时,平均每亩地的用药量为 .
根据题意,列方程为 ,
解得 .
经检验, 是原分式方程的根,且符合实际.
答:无人机喷洒农药时,平均每亩地的用药量为 .
(2)该镇计划采购A,B两种型号喷药无人机共20台.已知A型号喷药无人机
每台15 000元,B型号喷药无人机每台20 000元,若采购资金不超过360 000
元,则最少需采购A型号喷药无人机多少台
[答案] 设采购A型号喷药无人机 台.
根据题意,得 ,
解得 .
答:最少需采购A型号喷药无人机8台.
3.【新情境】健康中国,营养先行.2024年5月12日 日是第十届全民营养周,
社区食堂在全民营养周到来之际,推出系列营养套餐,其中营养套餐A的菜品如
下图所示.
_____________________________________________________________________________________________________________________________________________________________
(1)该套餐中的蛋白质和脂肪这两类营养素主要来自清蒸鱼块和滑炒鸡丁.
每100克清蒸鱼块和滑炒鸡丁中的蛋白质和脂肪含量如下表所示.按配餐要求,
每份套餐中清蒸鱼块和滑炒鸡丁两道菜品提供的蛋白质、脂肪量应分别为34
克、24.8克,求每份该种套餐中清蒸鱼块和滑炒鸡丁两道菜品各有多少克.
清蒸鱼块(每100克) 滑炒鸡丁(每100克)
蛋白质/克 16 15
脂肪/克 8 14
[答案] 设每份该种套餐中清蒸鱼块有克,滑炒鸡丁有 克.
根据题意,得
解得
答:每份该种套餐中清蒸鱼块有100克,滑炒鸡丁有120克.
(2)按配餐要求,每份素炒时蔬中芹菜与西蓝花共260克,已知每100克芹菜
与每100克西蓝花分别含有1.5克、2.5克的膳食纤维.若要使每份素炒时蔬中所
含的膳食纤维不少于5克,则每份素炒时蔬中西蓝花至少有多少克
[答案] 设每份素炒时蔬中西蓝花有 克.
根据题意,得 ,
解得 ,
所以 的最小值为110.
答:每份素炒时蔬中西蓝花至少有110克.
类型2 利用函数解决实际问题
4.某学校计划一次性购买A,B两种类型的书架,用于建设班级读书角,方便
学生利用课余时间阅览图书.已知购买3个A型书架和4个B型书架共需640元,
购买5个A型书架和2个B型书架共需670元.
(1)求购买一个A型书架和一个B型书架各需多少元.
[答案] 设购买一个A型书架需要元,购买一个B型书架需要 元,
根据题意,得
解得
答:购买一个A型书架需要100元,购买一个B型书架需要85元.
(2)该学校打算购买A,B两种类型的书架共52个,且购买的总费用不超过4
700元.若A型书架的最大放书量为80册,B型书架的最大放书量为65册,请设
计出放书总量最大的购买方案,并说明理由.
[答案] 放书总量最大的购买方案为购买18个A型书架,34个B型书架.
理由:设购买个A型书架,则购买 个B型书架,
根据题意,得 ,
解得 .
设购买两种类型书架的放书总量为 册,
则 .
,随 的增大而增大.
又,且 为整数,
当时,取得最大值,此时 ,
放书总量最大的购买方案为:购买18个A型书架,34个B型书架.
5.某市为了科学处理垃圾,新建了A,B两类垃圾处理场共20个,其中A类垃
圾处理厂处理不可回收垃圾,B类垃圾处理厂处理可回收垃圾,已知每一个
A类垃圾处理场日处理量为30吨,每一个B类垃圾处理场日处理量为40吨,
该市新建的20个垃圾处理场每天处理城市垃圾总量为720吨.
(1)求该市新建的A,B两类垃圾处理场各有多少个.
[答案] 设A类垃圾处理场有个,B类垃圾处理场有 个,
根据题意,得
解得
答:A类垃圾处理场有8个,B类垃圾处理场有12个.
(2)为了环保要求,该市将不可回收垃圾再次细分为不可回收垃圾和有害
垃圾,致使A类垃圾处理场日处理量减少了5吨,市政府拟将 个B类
垃圾处理场改建成A类垃圾处理场,请给出两类垃圾处理场日处理垃圾总量
最大的改建方案,并求出日处理垃圾总量的最大值.
[答案] 若A类垃圾处理场增加个,则B类垃圾处理场为 个.
设两类垃圾处理场日处理垃圾总量为 吨,则
.
,随着 的增大而减小.
又 ,
当 时,改建后两类垃圾处理场日处理垃圾总量最大,
(吨).
答:将3个B类垃圾处理场改建成A类垃圾处理场,两类垃圾处理场日处理垃
圾总量最大,为635吨.
6.近年来,市民交通安全意识逐步增强,头盔需求量增大.某生产厂家销售甲、
乙两种头盔,已知甲种头盔比乙种头盔的单价多11元,购进甲种头盔10个,
乙种头盔20个,共需1 730元.
(1)求甲、乙两种头盔的单价.
[答案] 设甲、乙两种头盔的单价分别为元、 元.
由题意列方程组得解得
答:甲、乙两种头盔的单价分别为65元、54元.
(2)某商店欲购进两种头盔共100个,正好赶上厂家进行促销活动,促销方
式如下:甲种头盔按单价的8折出售,乙种头盔每个降价6元出售.如果此次购
买甲种头盔的数量不低于乙种头盔的数量,那么购买多少个甲种头盔可以使
此次购买头盔的总费用最少 最少费用是多少元
[答案] 设购买甲种头盔个,则购买乙种头盔 个,
根据题意,得,解得 .
设此次购买头盔的总费用为 元,
则 .
,随 的增大而增大.
当时, 有最小值,
.
答:购买50个甲种头盔可以使此次购买头盔的总费用最少,最少费用是
5 000元.
7.星期日上午 ,小明从家里出发步行
前往离家 的镇海书城参加读书会活
动,他以的速度步行了
后发现忘带入场券,于是他停下来,打电
话给家里的爸爸寻求帮助.9:15爸爸骑着自
行车从家里出发,沿着同一路线以
的速度行进,同一时刻小明继续按原速步行赶往目的地.爸爸追
上小明后载上他以相同的车速前往书城(停车载人时间忽略不计),到达书
城后爸爸原速返回家.爸爸和小明离家的路程与小明所用时间 的
函数关系如图所示.
(1)求爸爸在到达镇海书城前,他离开家的路程关于的函数表达式及 的
值.
[答案] 方法一:爸爸到达镇海书城所用时间为 ,
设爸爸在到达镇海书城前,他离开家的路程关于 的函数表达式为
,
把,分别代入 ,
得
解得
爸爸在到达镇海书城前,他离开家的路程关于 的函数表达式为
.
爸爸的速度不变,
他返回家的时间和到达书城的时间均为 ,
.
方法二:由题意知,爸爸在小明出发后出发,速度为 ,
爸爸在到达镇海书城前,他离开家的路程
.
又 爸爸的速度不变,
.
(2)爸爸出发多长时间后追上小明?此时距离镇海书城还有多远?
[答案] 设爸爸出发 后追上小明,
则 ,
解得 ,
.
答:爸爸出发后追上小明,此时距离镇海书城还有 .
8.近年来,直播带货成了一个火热的新兴职业.某主播带货图书《苏东坡传》,
他用双语直播,风趣幽默,点燃了观众的读书热情.已知这本书的进价为10元,
规定售价不低于进价,且不高于进价的3倍,通过前几天的销售发现,该书
每天的销售量(本)与售价 (元 /本)之间近似满足一次函数关系,部分
对应数据如下表所示:
(元/本) … 15 25 …
本 … 700 500 …
(1)根据表格提供的数据,求与的函数关系式,并写出 的取值范围.
[答案] 设与的函数关系式为 .
依题意,得
解得
与的函数关系式为 .
(2)若销售该书每天的利润为6 000元,求该书的售价.
[答案] 依题意,得 ,
整理,得 ,
解得, .
, .
若销售该书每天的利润为6 000元,则该书的售价为20元/本.
(3)销售该书每天的利润能否达到9 000元 请说明理由.
[答案] 不能.理由如下.
方法一:依题意,得 ,
整理,得 .
,
该方程没有实数根,
销售该书每天的利润不能达到9 000元.
方法二:设销售该书每天的利润为 元,则
.
当时,有最大值 ,即销售该书每天的最大利润为8 000元.
,
销售该书每天的利润不能达到9 000元.
9.【新考法】学科实践
驱动任务:“过水门”是国际民航中高级别的礼仪,因两辆(或以上)的消防车
在飞机两侧喷射水柱出现一个“水门”状的效果而得名(如图(1)).学校计
划在运动会开幕式上举行彩旗队“过水门”仪式,数学研习小组协助彩旗队进行
队列设计.
研究步骤:①如图(2),研习小组测得表演场地的宽度米,在, 处各
安装一个接通水源的喷泉喷头,将出水口高度, 都设为1米,调整出水速度
与角度,使喷出的两条抛物线形水柱形状相同,并在抛物线顶点 处相遇,组成
一条完整的抛物线形水门,且点 到地面的距离为5米;
②研习小组了解到彩旗队的队列设置要求,每两列之间保持相同的间距,队员
所持彩旗的顶端离地面的距离保持3.6米.
图(1)
图(2)
问题解决:请根据上述研究步骤与相关数据,完成下列任务.
(1)以线段所在直线为轴,的垂直平分线为 轴建立平面直角坐标系,
请在图中画出坐标系,并求出“过水门”仪式中水柱所在抛物线的函数表达式;
[答案] 建立如图所示的平面直角坐标系.
设所求抛物线的函数表达式为 ,
由题可知,米, ,
米, 米,
所以,点的坐标为,点的坐标为, .
将,代入 ,
得
解得
所以,所求抛物线的函数表达式为 .
(2)为保证“水门”的水柱不被破坏,要求队列最外侧的两列同学所持彩旗顶
端与水柱间的铅直距离为0.4米,若彩旗队要排成6列纵队,请你通过计算,确定
彩旗队“过水门”时,每相邻两列纵队的间距.
[答案] 如图,分别过最外侧队员彩旗顶端作 轴的
垂线,,垂足为点,,分别交抛物线于点, .
由题意可知, (米),
所以,点, 的纵坐标均为4.
当时, ,
解得 ,
点,的坐标分别为和 .
所以,最外侧两列彩旗队之间的距离为 (米).
所以, (米).
答:彩旗队每相邻两列纵队的间距为1.6米.
同课章节目录
