2025年中考数学专项复习--题型四 尺规作图题 课件(共43张PPT)
文档属性
| 名称 | 2025年中考数学专项复习--题型四 尺规作图题 课件(共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 13:56:36 | ||
图片预览

文档简介
(共43张PPT)
题型四 尺规作图题
中考题型专项突破
2025年中考数学一轮复习
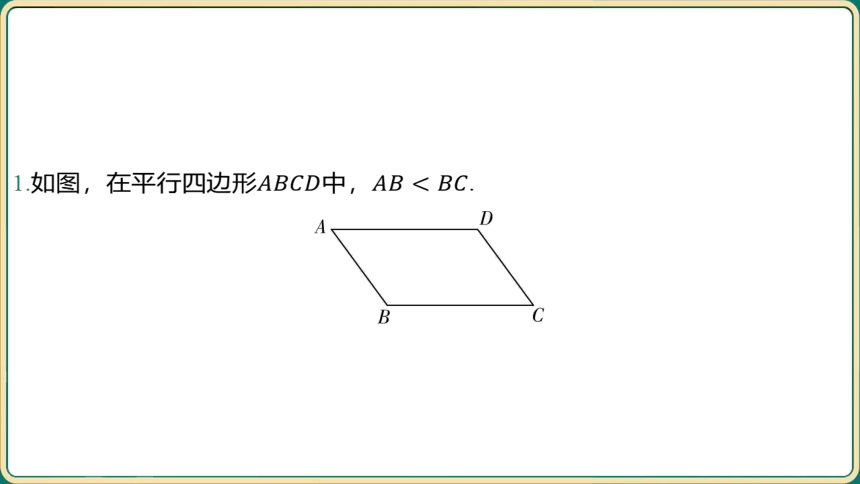
1.如图,在平行四边形中, .
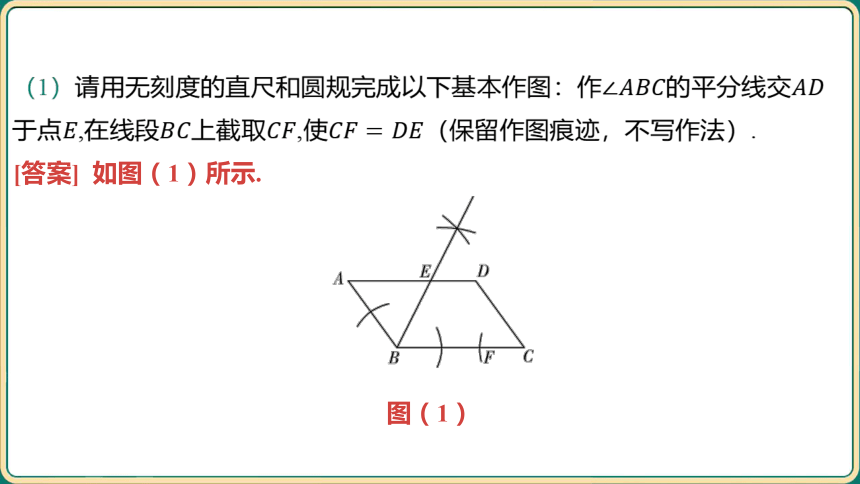
(1)请用无刻度的直尺和圆规完成以下基本作图:作的平分线交
于点,在线段上截取,使 (保留作图痕迹,不写作法).
[答案] 如图(1)所示.
图(1)
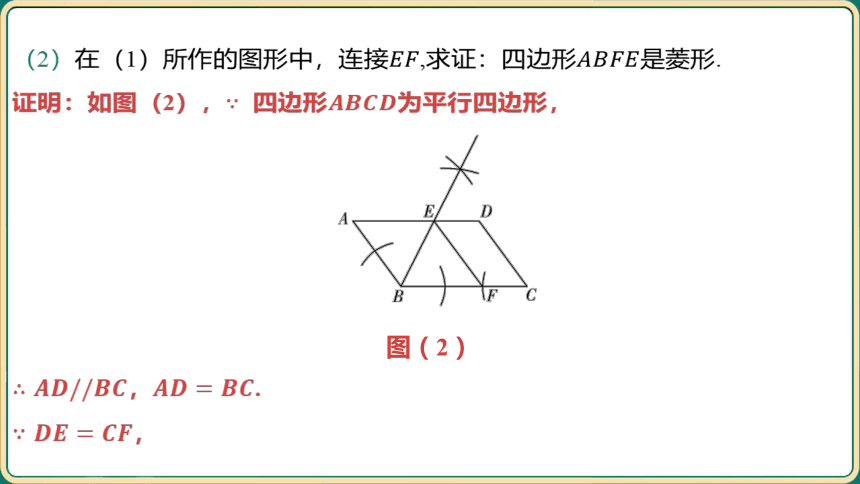
(2)在(1)所作的图形中,连接,求证:四边形 是菱形.
证明:如图(2), 四边形 为平行四边形,
图(2)
, .
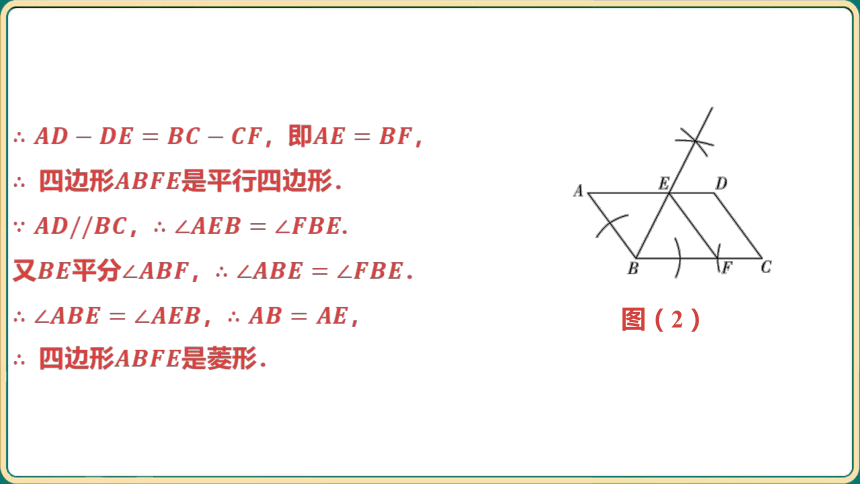
,
,即 ,
四边形 是平行四边形.
, .
又平分, .
, ,
四边形 是菱形.
图(2)
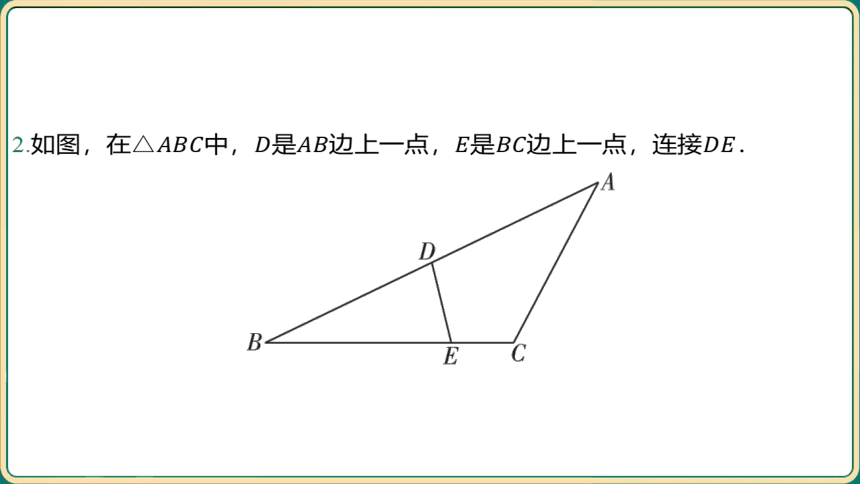
2.如图,在中,是边上一点,是边上一点,连接 .
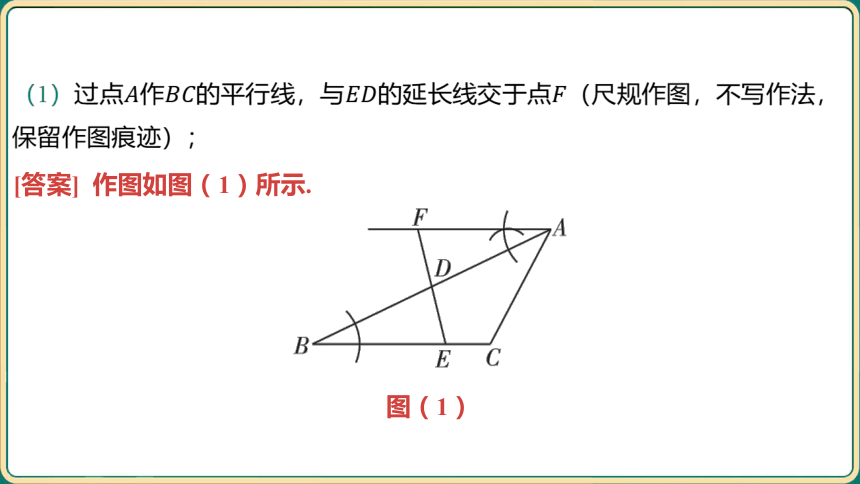
(1)过点作的平行线,与的延长线交于点 (尺规作图,不写作法,
保留作图痕迹);
[答案] 作图如图(1)所示.
图(1)
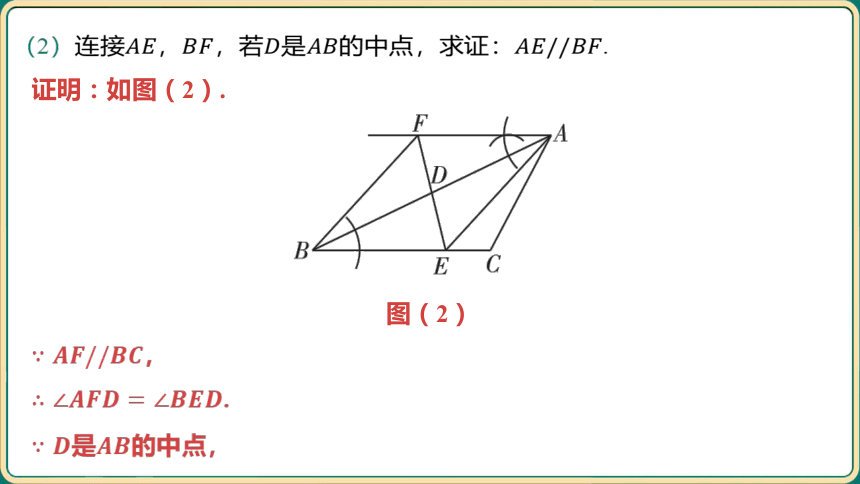
(2)连接,,若是的中点,求证: .
证明:如图(2).
图(2)
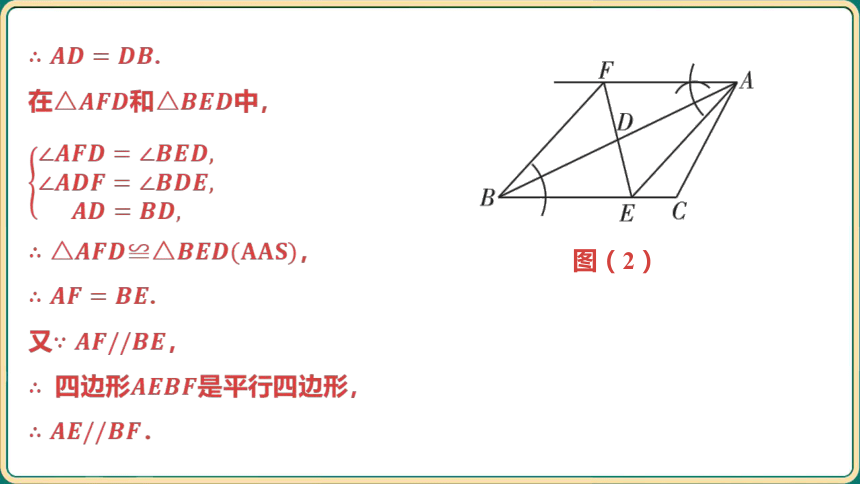
,
.
是 的中点,
.
在和 中,
,
.
又 ,
四边形 是平行四边形,
.
图(2)
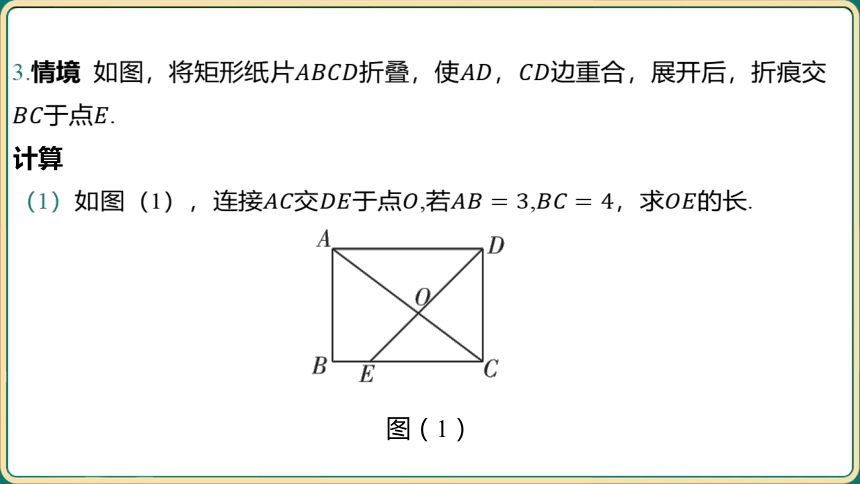
3.情境 如图,将矩形纸片折叠,使, 边重合,展开后,折痕交
于点 .
计算
(1)如图(1),连接交于点,若,,求 的长.
图(1)
[答案] 由题意知,,平分 ,
,
, .
, ,
,
.
图(1)
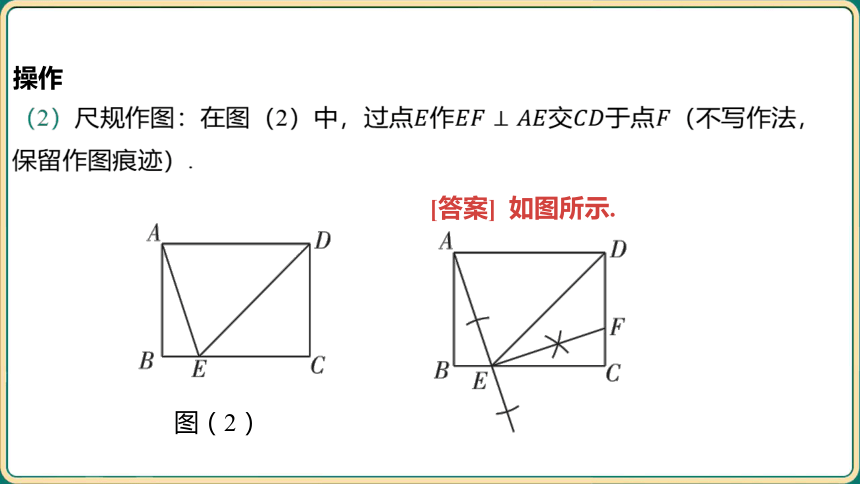
操作
(2)尺规作图:在图(2)中,过点作交于点 (不写作法,
保留作图痕迹).
图(2)
[答案] 如图所示.
证明
(3)求证: .
证明:由(1)可知 .
又, .
,
.
又 ,
.
又, ,
.
4.如图,点是正方形的边上一个动点,连接,点是 上一点,且
.
(1)请用无刻度的直尺和圆规作出点 (保留作图痕迹,不写作法).
[答案] 作图如图(1)所示(作法不唯一).
图(1)
(2)延长交于点,求证: .
证明:如图(1), 四边形 是正方形,
, .
由作图知, .
又 , ,
, .
图(1)
(3)随着点在边上运动,当时,求线段 长的最小值.
[答案] ,点在线段 上,
点在以 为直径的一段圆弧上运动,如图(2).
图(2)
设的中点为,连接,交圆弧于点 ,
此时 的长度最小.
在中, ,
,即线段长的最小值为 .
图(2)
5.【新情境】下面是某公众号发布的一篇数学短文,请你认真阅读,并完成相应
的任务.
用尺规实现相似图形的面积加倍
尺规作图是起源于古希腊的数学课题,只使用圆规和直尺,并且只准许使
用有限次,以解决不同的平面几何作图问题.我们可以利用尺规将一个图形的
面积加倍,并保持所得图形与原图形相似.
例如:如图(1),已知正方形 .
__________________________________________
图(1)
求作:正方形,使正方形的面积是正方形 面积的2倍,且
点,分别在, 的延长线上.
作法:①连接,作射线, ;
②以点为圆心,长为半径画弧,分别交射线,于点, ;
③分别以点,为圆心,长为半径画弧,两弧在内部交于点 ;
④连接,,则四边形 即为所求.
事实上,以正方形 的对角线的长为边长的正方形都符合要求!
……
任务:
(1)按照材料中的作法,在图(1)中作出正方形 ;
[答案] 如图,正方形 即为所求.
(2)如图(2),已知是的直径,求作:,使的面积是 面积
的2倍.(要求:尺规作图,保留作图痕迹,不写作法)
图(2)
[答案] 如图, 即为所求.
6.如图,四边形内接于,为的直径,,点 为劣弧
上一点,且 .
(1)求作点,连接,延长,交于点 (尺规作图,保留作图痕迹,
不写作法).
[答案] 作图如图(1)所示.
图(1)
①求证: 为等腰三角形;
图(2)
[答案] 证法一(借助全等三角形及等量代换求证):
如图(2),连接, .
,
.
,
, .
又 ,
,
,
,
为等腰三角形.
(2)在(1)所作的图中,连接 .
证法二(借助“等角对等边”求证):如图(3),连接, .
图(3)
为 的直径,
.
,
,
,
,
,
.
四边形内接于 ,
.
,
图(3)
.
,
,
,
,
,
为等腰三角形.
图(3)
②若,,求弦 的长.
[答案] 如图(3),连接, .
, ,
.
由①知 ,
.
, ,
.
,
图(3)
.
为 的直径,
,
.
,
,
.
,
图(3)
,
,
,
.
图(3)
7.为的内接三角形,其中 ,请完成以下探究.
(1)请在图(1)中用圆规和直尺画出满足条件的所有等腰三角形
(尺规作图,保留作图痕迹,不写作法).
图(1)
备用图
[答案] 如图(1),及 即为所求.
图(1)
图(2)
(2)如图(2),连接并延长交于点,交 于
点,过点作于点,记, .
①求关于 的函数表达式(不必写自变量的取值范围);
[答案] 如图(2),连接,过点作于点 ,
图(2)
, ,
.
又 ,
,
,
,
,
,
关于的函数表达式为 .
图(2)
②若点为的三等分点,求 的值.
[答案] 如图(3),连接并延长交于点,连接 ,
图(3)
易知, .
又为 的直径,
.
, ,
为 的中位线,
, ,
,
,即 .
点为 的三等分点,
可分两种情况讨论.
图(3)
当时, ,
,
此种情形不存在.
图(3)
当时,如图(4), ,
图(4)
,
.
在中, ,
方法一: ,
.
图(4)
方法二: ,
.
由①知, ,
,即 ,
.
,
,
,
.
图(4)
题型四 尺规作图题
中考题型专项突破
2025年中考数学一轮复习
1.如图,在平行四边形中, .
(1)请用无刻度的直尺和圆规完成以下基本作图:作的平分线交
于点,在线段上截取,使 (保留作图痕迹,不写作法).
[答案] 如图(1)所示.
图(1)
(2)在(1)所作的图形中,连接,求证:四边形 是菱形.
证明:如图(2), 四边形 为平行四边形,
图(2)
, .
,
,即 ,
四边形 是平行四边形.
, .
又平分, .
, ,
四边形 是菱形.
图(2)
2.如图,在中,是边上一点,是边上一点,连接 .
(1)过点作的平行线,与的延长线交于点 (尺规作图,不写作法,
保留作图痕迹);
[答案] 作图如图(1)所示.
图(1)
(2)连接,,若是的中点,求证: .
证明:如图(2).
图(2)
,
.
是 的中点,
.
在和 中,
,
.
又 ,
四边形 是平行四边形,
.
图(2)
3.情境 如图,将矩形纸片折叠,使, 边重合,展开后,折痕交
于点 .
计算
(1)如图(1),连接交于点,若,,求 的长.
图(1)
[答案] 由题意知,,平分 ,
,
, .
, ,
,
.
图(1)
操作
(2)尺规作图:在图(2)中,过点作交于点 (不写作法,
保留作图痕迹).
图(2)
[答案] 如图所示.
证明
(3)求证: .
证明:由(1)可知 .
又, .
,
.
又 ,
.
又, ,
.
4.如图,点是正方形的边上一个动点,连接,点是 上一点,且
.
(1)请用无刻度的直尺和圆规作出点 (保留作图痕迹,不写作法).
[答案] 作图如图(1)所示(作法不唯一).
图(1)
(2)延长交于点,求证: .
证明:如图(1), 四边形 是正方形,
, .
由作图知, .
又 , ,
, .
图(1)
(3)随着点在边上运动,当时,求线段 长的最小值.
[答案] ,点在线段 上,
点在以 为直径的一段圆弧上运动,如图(2).
图(2)
设的中点为,连接,交圆弧于点 ,
此时 的长度最小.
在中, ,
,即线段长的最小值为 .
图(2)
5.【新情境】下面是某公众号发布的一篇数学短文,请你认真阅读,并完成相应
的任务.
用尺规实现相似图形的面积加倍
尺规作图是起源于古希腊的数学课题,只使用圆规和直尺,并且只准许使
用有限次,以解决不同的平面几何作图问题.我们可以利用尺规将一个图形的
面积加倍,并保持所得图形与原图形相似.
例如:如图(1),已知正方形 .
__________________________________________
图(1)
求作:正方形,使正方形的面积是正方形 面积的2倍,且
点,分别在, 的延长线上.
作法:①连接,作射线, ;
②以点为圆心,长为半径画弧,分别交射线,于点, ;
③分别以点,为圆心,长为半径画弧,两弧在内部交于点 ;
④连接,,则四边形 即为所求.
事实上,以正方形 的对角线的长为边长的正方形都符合要求!
……
任务:
(1)按照材料中的作法,在图(1)中作出正方形 ;
[答案] 如图,正方形 即为所求.
(2)如图(2),已知是的直径,求作:,使的面积是 面积
的2倍.(要求:尺规作图,保留作图痕迹,不写作法)
图(2)
[答案] 如图, 即为所求.
6.如图,四边形内接于,为的直径,,点 为劣弧
上一点,且 .
(1)求作点,连接,延长,交于点 (尺规作图,保留作图痕迹,
不写作法).
[答案] 作图如图(1)所示.
图(1)
①求证: 为等腰三角形;
图(2)
[答案] 证法一(借助全等三角形及等量代换求证):
如图(2),连接, .
,
.
,
, .
又 ,
,
,
,
为等腰三角形.
(2)在(1)所作的图中,连接 .
证法二(借助“等角对等边”求证):如图(3),连接, .
图(3)
为 的直径,
.
,
,
,
,
,
.
四边形内接于 ,
.
,
图(3)
.
,
,
,
,
,
为等腰三角形.
图(3)
②若,,求弦 的长.
[答案] 如图(3),连接, .
, ,
.
由①知 ,
.
, ,
.
,
图(3)
.
为 的直径,
,
.
,
,
.
,
图(3)
,
,
,
.
图(3)
7.为的内接三角形,其中 ,请完成以下探究.
(1)请在图(1)中用圆规和直尺画出满足条件的所有等腰三角形
(尺规作图,保留作图痕迹,不写作法).
图(1)
备用图
[答案] 如图(1),及 即为所求.
图(1)
图(2)
(2)如图(2),连接并延长交于点,交 于
点,过点作于点,记, .
①求关于 的函数表达式(不必写自变量的取值范围);
[答案] 如图(2),连接,过点作于点 ,
图(2)
, ,
.
又 ,
,
,
,
,
,
关于的函数表达式为 .
图(2)
②若点为的三等分点,求 的值.
[答案] 如图(3),连接并延长交于点,连接 ,
图(3)
易知, .
又为 的直径,
.
, ,
为 的中位线,
, ,
,
,即 .
点为 的三等分点,
可分两种情况讨论.
图(3)
当时, ,
,
此种情形不存在.
图(3)
当时,如图(4), ,
图(4)
,
.
在中, ,
方法一: ,
.
图(4)
方法二: ,
.
由①知, ,
,即 ,
.
,
,
,
.
图(4)
同课章节目录
