2025年中考数学专项复习--题型一 统计与概率题 课件(共34张PPT)
文档属性
| 名称 | 2025年中考数学专项复习--题型一 统计与概率题 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 13:56:13 | ||
图片预览










文档简介
(共34张PPT)
题型一 统计与概率题
中考题型专项突破
2025年中考数学一轮复习
类型1 统计图表
1.【新角度】为了鼓励同学们多读书、读好书,某校开展了主题为“走进图书
馆·悦享书世界”的读书活动.综合实践小组的同学想要了解本校学生在这次
活动中借阅图书的情况,于是从全校1 200名学生中随机抽取200名学生,并
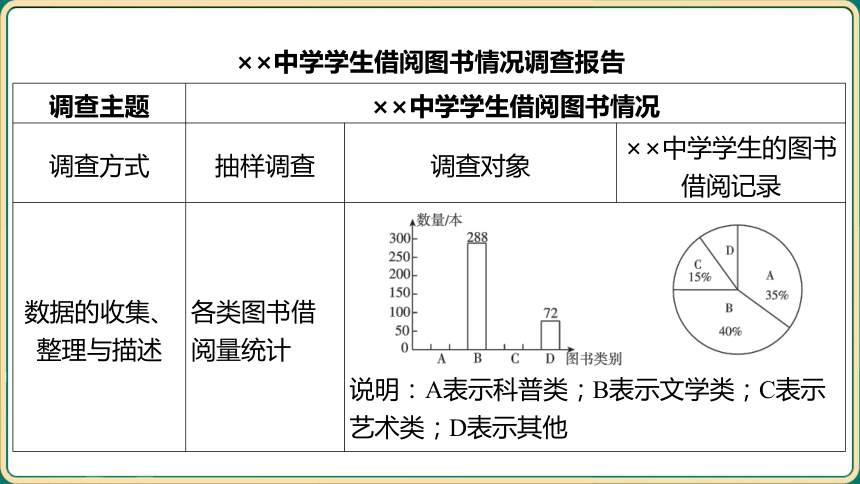
对这200名学生的图书借阅记录进行统计,形成了如下不完整的调查报告:
××中学学生借阅图书情况调查报告
调查主题 ××中学学生借阅图书情况 调查方式 抽样调查 调查对象 ××中学学生的图书
借阅记录
数据的收集、 整理与描述 各类图书借 阅量统计 __________________________________________________________________________________________________________ 说明:A表示科普类;B表示文学类;C表示 艺术类;D表示其他 调查主题 ××中学学生借阅图书情况 数据的收集、 整理与描述 学生个人借 阅量统计 __________________________________________________________________________________________________________
调查结论 …… 请根据以上调查报告,解答下列问题:
(1)求被调查的200名学生在本次活动中借阅图书的总数量,并将条形统计
图补充完整.
[答案] (本).
答:被调查的200名学生在本次活动中借阅图书的总数量为720本.
补全条形统计图如下:
(2)估计该校所有学生中,图书借阅数量为3本及以上的学生人数.
[答案] (名).
答:估计该校所有学生中,图书借阅数量为3本及以上的学生有582名.
(3)在制定方案时,小亮给出的初步方案是随机抽取200名九年级学生,并
对他们的图书借阅记录进行统计.但经过小组讨论,方案被否决了.请指出
该方案被否决的原因.
[答案] 小亮在选择样本时出现问题,小组想了解全校学生在读书活动中图书
的借阅情况,他只是在九年级学生中选择调查对象,因此样本的选择不具备
代表性.(写出一条,言之有理即可)
2.社会发展日新月异,企业唯有与时俱进,才能破茧成蝶、
破壳发展.某醋厂秉持科技创新的理念,不断推陈出
新.为开发一种新的风味醋,醋厂研发组采用甲、乙两种
技术方案进行实验,每种方案各设置100个实验样品.经
过一段时间后,研发组从两组实验样品中各随机抽取20个
作为样本,对每个样本的指标进行综合评分(满分100分,单位:分),并
对相关数据进行整理和分析(用 表示综合评分,数据分成5组:A.
;B.;C.;D.; .
.注:90分及以上为优等).
【数据收集与整理】
甲方案20个样本 的综合评分 59,86,77,87,78,73,79,69,84,91,85,91,6 4,85,59,78,64,70,75,86. 甲方案样本综合 评分统计 A. 2
B. 3
C. 7
D. 6
E.
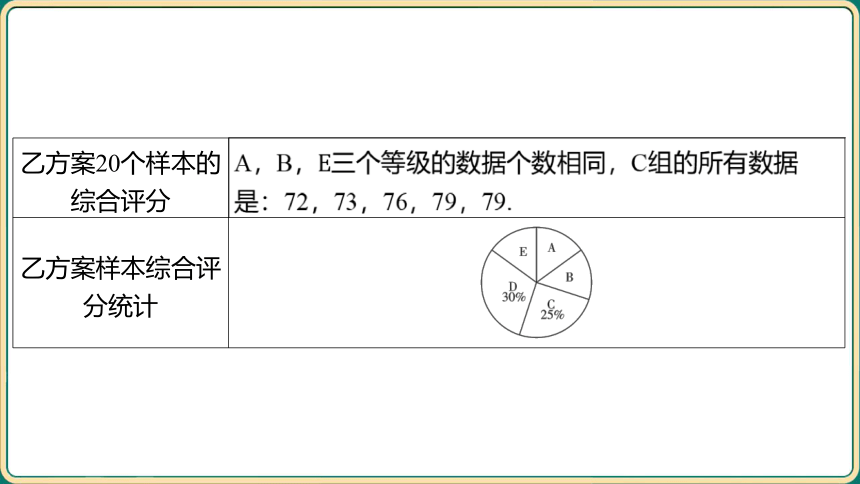
乙方案20个样本的 综合评分 A,B, 三个等级的数据个数相同,C组的所有数据
是:72,73,76,79,79.
乙方案样本综合评 分统计 _______________________________
【数据分析】
样本综合评分情况分析 平均数 中位数 方差 优等率
甲方案 77 78 97.8
乙方案 77 86.5
根据以上信息,解答下列问题:
(1)直接写出上述材料中空缺的数据:___,____, ______.
2
79
(2)经过评估,研发组认为乙方案优于甲方案,你认为他们的结论合理吗?
请结合“数据分析”中的四种数据说明理由.
[答案] 合理.
理由:根据统计表提供的信息,甲、乙两个方案的平均分相同,但是其他统
计量不同.从优等率看,乙方案为,甲方案为 ,乙方案中优等实验
样品的数量高于甲方案中优等实验样品的数量,乙方案优于甲方案;
从中位数看,乙方案的中位数为79分,甲方案的中位数为78分,乙方案样本
综合评分的中位数高于甲方案样本综合评分的中位数,乙方案优于甲方案;
从方差看,乙方案样本综合评分的方差小于甲方案样本综合评分的方差,说
明乙方案的实验样品品质更为稳定.
综上所述,乙方案优于甲方案.
(3)研发组计划对两种方案中综合评分为“优等”的实验样品进行第二阶段
的指标分析,请估计第二阶段指标分析的实验样品共有多少个.
[答案] (个).
答:估计第二阶段指标分析的实验样品共有25个.
3.【新考法】为更好推动数字化教育,某校组织七、八年级的学生开展为期
五天的信息素养提升实践活动,计划开设五场主题活动.为了解学生的活动
意向,学校在七、八年级各随机抽取40名同学进行问卷调查(调查问卷如图,
收回全部问卷且都有效),并将调查结果绘制成如下的条形统计图和扇形统
计图(均不完整).
信息素养提升实践活动意向调查问卷
请在下列选项中选择一项活动意向,并在其后“□”内打 (每位同学必须且
只能选择其中一项).
A.创意编程□B. 创意设计□C.智能博物□D.电脑绘图□ E.优创未来□
请根据以上信息,解答下列问题:
(1)补全条形统计图和扇形统计图空缺的部分;
[答案] 补全条形统计图和扇形统计图如下:
活动意向调查结果统计图
七、八年级学生活动意向分布情况
统计图
(2)已知该校七、八年级学生共有1 000人参加本次实践活动(每人只参加
一场主题活动),活动地点安排在两个多功能厅,学校根据调查结果给出五
场主题活动的具体时间和地点的预案,其中主题活动C,D的时间和地点已
确定,请你合理安排A,B, 三场主题活动的时间和地点,补全活动安排表
格(写出一种方案即可),并说明理由.
时间 星期一 星期二 星期三 星期四 星期五
地点 南院多功 能厅 (容纳 350人) 北院多功 能厅 (容纳 160人) 南院多功 能厅 (容纳 350人) 北院多功能厅 (容纳160人) 北院多功能厅
(容纳160人)
主题 活动 ___ ___ C ___ D
[答案] 活动安排为:
时间 星期一 星期二 星期三 星期四 星期五
地点 南院多功 能厅 (容纳 350人) 北院多功 能厅 (容纳 160人) 南院多功能厅 (容纳 350人) 北院多功能厅 (容纳160人) 北院多功能厅
(容纳160人)
主题 活动 A C B D
或
时间 星期一 星期二 星期三 星期四 星期五
地点 南院多功能厅 (容纳 350人) 北院多功能厅 (容纳 160人) 南院多功能厅 (容纳 350人) 北院多功能厅 (容纳160人) 北院多功能厅
(容纳160人)
主题 活动 B C A D
理由如下:根据统计图提供的信息,
参加主题活动A的学生人数约为 (人);
参加主题活动B的学生人数约为 (人);
参加主题活动的学生人数约为 (人);
所以主题活动 只能安排在南院多功能厅星期一进行;主题活动A和主题活
动B安排在北院多功能厅均可满足容纳人数的要求,星期二或星期四两天都
可以安排.
类型2 随机事件的概率
4.甲、乙两陌生人乘坐同一趟高铁列车从唐山前往北京.如图,网上购票时,购
票系统向两人都推送了第2车厢第13排的座位,其中座位D已有人预定,两人只
能在A,B,C, 四个座位选择一个座位,且选择这四个座位的可能性相同.
(1)求甲选择A座位的概率;
[答案] 由题意得甲可选择的座位有4个,且选择每个座位的可能性相同,
甲选择A座位的概率为 .
(2)用列表法或画树状图法求出甲、乙二人座位相邻的概率.
[答案] 根据题意,列表如下:
A B C
A
B
C
共有12种等可能的结果,甲、乙二人座位相邻的结果有4种,故所求概率
为 .
5.某超市为回馈广大消费者,在开业周年之际举行摸球抽奖活动.在一个不
透明的口袋中装有1个白球和2个红球,这些球除颜色外完全相同.
(1)从袋中随机摸出一个球,则摸出的这个球是红球的概率是__.
(2)活动设置了一等奖和二等奖两个奖项,一等奖的获奖率低于二等
奖.摸球规则如下:从袋中随机摸出一个球,不放回,再从袋中剩余的两个
球中随机摸出一个球.规定摸出颜色不同的两球和摸出颜色相同的两球分别
对应不同奖项,请写出它们分别对应的奖项,并说明理由.
[答案] 根据题意,画树状图如下.
由树状图可知,共有6种等可能的结果,其中摸出颜色不同的两球的结果有4种,
摸出颜色相同的两球的结果有2种,
摸出颜色不同的两球的概率为,摸出颜色相同的两球的概率为 .
一等奖的获奖率低于二等奖, ,
摸出颜色不同的两球对应的奖项为二等奖,摸出颜色相同的两球对应的奖
项为一等奖.
6.2024年巴黎奥运会新增霹雳舞、滑板、攀岩、冲浪四个项目.为了更好地观
赏这些项目,学校在四个场所开展了这四个项目的竞技知识讲座,要求每位学
生参与其中一场讲座.九(1)班在不透明的袋子中放置四个大小、质地一样
的小球,编号为1,2,3,4.
(1)若1号表示霹雳舞,2号表示滑板,3号表示攀岩,4号表示冲浪.第一位同学
从袋子中摸出一球,记录球号后放回袋子中,摇匀后让第二位同学摸出一
球……摸到球号是多少就去参加对应项目的讲座,求该班的小明和小华同学都
选中参加霹雳舞讲座的概率.
[答案] 根据题意画树状图如下:
由树状图可知,共有16种等可能的结果,其中两人都选中参加霹雳舞讲座的结
果有1种,所以小明和小华同学都选中参加霹雳舞讲座的概率是 .
(2)小明和小华同学都有霹雳舞基础,霹雳舞会场将从他们两人中选一人去
辅助教学.他俩都想去,于是商定:从袋子中一次性摸出两个球,若球号之和大于
5,则小明去辅助教学,否则小华去.他们商定的方案公平吗 若不公平,请修改游
戏规则使游戏公平.
[答案] 不公平.
理由:从袋子中随机摸出两球的结果有,,,,, ,
共6种等可能的结果,其中球号之和大于5的结果有2种, 小明去辅助教学的概
率为,而小华去辅助教学的概率为 .
, 他们商定的方案不公平.
游戏规则可以改为:从袋子中一次性摸出两个球,若球号之积大于5,则小明去
辅助教学,否则小华去.
类型3 统计与概率综合
7.某公司计划购入语音识别输入软件来提高办公效率.市面上有A,B两款语
音识别输入软件,该公司准备择优购买.为了解两款软件的性能,测试员小
敏随机选取了20个句子,其中每句都含10个字.她用标准普通话以相同的语
速朗读每个句子来测试这两款软件,并将语音识别结果进行了整理、描述和
分析,下面给出了部分信息:
A款软件每个句子中识别正确的 字数记录: 5,5,6,6,6, 6,6,6,7,7, 8,9,9,9,9, 10,10,10,10,10. B款软件每个句子中识别正确的字数的折
线统计图:
__________________________________________________
A,B两款软件每个句子中识别正确的字数的统计表如下.
软件 平均数 众数 中位数 识别正确达到10个字的句子所占百分比
A款 7.7 7.5
B款 7.7 8
根据以上信息.解答下列问题:
(1)上述表中的___,___, ______;
6
8
(2)若会议记录员用A,B两款软件各识别了500个句子,每个句子有10个
字,请估计两款软件一字不差地识别正确的句子共有多少个;
[答案] (个).
答:估计两款软件一字不差地识别正确的句子共有175个.
(3)该公司现派一个三人采购小组前去购进一批语音识别输入软件,若每
人从这两款软件中随机选择一款,求他们三人都选择A款软件的概率.
[答案] 将采购小组的三人分别记为甲、乙、丙.
根据题意,画树状图如下:
由树状图可知,共有8种等可能的结果,其中他们三人都选择A款软件的结果
有1种,所以他们三人都选择A款软件的概率是 .
题型一 统计与概率题
中考题型专项突破
2025年中考数学一轮复习
类型1 统计图表
1.【新角度】为了鼓励同学们多读书、读好书,某校开展了主题为“走进图书
馆·悦享书世界”的读书活动.综合实践小组的同学想要了解本校学生在这次
活动中借阅图书的情况,于是从全校1 200名学生中随机抽取200名学生,并
对这200名学生的图书借阅记录进行统计,形成了如下不完整的调查报告:
××中学学生借阅图书情况调查报告
调查主题 ××中学学生借阅图书情况 调查方式 抽样调查 调查对象 ××中学学生的图书
借阅记录
数据的收集、 整理与描述 各类图书借 阅量统计 __________________________________________________________________________________________________________ 说明:A表示科普类;B表示文学类;C表示 艺术类;D表示其他 调查主题 ××中学学生借阅图书情况 数据的收集、 整理与描述 学生个人借 阅量统计 __________________________________________________________________________________________________________
调查结论 …… 请根据以上调查报告,解答下列问题:
(1)求被调查的200名学生在本次活动中借阅图书的总数量,并将条形统计
图补充完整.
[答案] (本).
答:被调查的200名学生在本次活动中借阅图书的总数量为720本.
补全条形统计图如下:
(2)估计该校所有学生中,图书借阅数量为3本及以上的学生人数.
[答案] (名).
答:估计该校所有学生中,图书借阅数量为3本及以上的学生有582名.
(3)在制定方案时,小亮给出的初步方案是随机抽取200名九年级学生,并
对他们的图书借阅记录进行统计.但经过小组讨论,方案被否决了.请指出
该方案被否决的原因.
[答案] 小亮在选择样本时出现问题,小组想了解全校学生在读书活动中图书
的借阅情况,他只是在九年级学生中选择调查对象,因此样本的选择不具备
代表性.(写出一条,言之有理即可)
2.社会发展日新月异,企业唯有与时俱进,才能破茧成蝶、
破壳发展.某醋厂秉持科技创新的理念,不断推陈出
新.为开发一种新的风味醋,醋厂研发组采用甲、乙两种
技术方案进行实验,每种方案各设置100个实验样品.经
过一段时间后,研发组从两组实验样品中各随机抽取20个
作为样本,对每个样本的指标进行综合评分(满分100分,单位:分),并
对相关数据进行整理和分析(用 表示综合评分,数据分成5组:A.
;B.;C.;D.; .
.注:90分及以上为优等).
【数据收集与整理】
甲方案20个样本 的综合评分 59,86,77,87,78,73,79,69,84,91,85,91,6 4,85,59,78,64,70,75,86. 甲方案样本综合 评分统计 A. 2
B. 3
C. 7
D. 6
E.
乙方案20个样本的 综合评分 A,B, 三个等级的数据个数相同,C组的所有数据
是:72,73,76,79,79.
乙方案样本综合评 分统计 _______________________________
【数据分析】
样本综合评分情况分析 平均数 中位数 方差 优等率
甲方案 77 78 97.8
乙方案 77 86.5
根据以上信息,解答下列问题:
(1)直接写出上述材料中空缺的数据:___,____, ______.
2
79
(2)经过评估,研发组认为乙方案优于甲方案,你认为他们的结论合理吗?
请结合“数据分析”中的四种数据说明理由.
[答案] 合理.
理由:根据统计表提供的信息,甲、乙两个方案的平均分相同,但是其他统
计量不同.从优等率看,乙方案为,甲方案为 ,乙方案中优等实验
样品的数量高于甲方案中优等实验样品的数量,乙方案优于甲方案;
从中位数看,乙方案的中位数为79分,甲方案的中位数为78分,乙方案样本
综合评分的中位数高于甲方案样本综合评分的中位数,乙方案优于甲方案;
从方差看,乙方案样本综合评分的方差小于甲方案样本综合评分的方差,说
明乙方案的实验样品品质更为稳定.
综上所述,乙方案优于甲方案.
(3)研发组计划对两种方案中综合评分为“优等”的实验样品进行第二阶段
的指标分析,请估计第二阶段指标分析的实验样品共有多少个.
[答案] (个).
答:估计第二阶段指标分析的实验样品共有25个.
3.【新考法】为更好推动数字化教育,某校组织七、八年级的学生开展为期
五天的信息素养提升实践活动,计划开设五场主题活动.为了解学生的活动
意向,学校在七、八年级各随机抽取40名同学进行问卷调查(调查问卷如图,
收回全部问卷且都有效),并将调查结果绘制成如下的条形统计图和扇形统
计图(均不完整).
信息素养提升实践活动意向调查问卷
请在下列选项中选择一项活动意向,并在其后“□”内打 (每位同学必须且
只能选择其中一项).
A.创意编程□B. 创意设计□C.智能博物□D.电脑绘图□ E.优创未来□
请根据以上信息,解答下列问题:
(1)补全条形统计图和扇形统计图空缺的部分;
[答案] 补全条形统计图和扇形统计图如下:
活动意向调查结果统计图
七、八年级学生活动意向分布情况
统计图
(2)已知该校七、八年级学生共有1 000人参加本次实践活动(每人只参加
一场主题活动),活动地点安排在两个多功能厅,学校根据调查结果给出五
场主题活动的具体时间和地点的预案,其中主题活动C,D的时间和地点已
确定,请你合理安排A,B, 三场主题活动的时间和地点,补全活动安排表
格(写出一种方案即可),并说明理由.
时间 星期一 星期二 星期三 星期四 星期五
地点 南院多功 能厅 (容纳 350人) 北院多功 能厅 (容纳 160人) 南院多功 能厅 (容纳 350人) 北院多功能厅 (容纳160人) 北院多功能厅
(容纳160人)
主题 活动 ___ ___ C ___ D
[答案] 活动安排为:
时间 星期一 星期二 星期三 星期四 星期五
地点 南院多功 能厅 (容纳 350人) 北院多功 能厅 (容纳 160人) 南院多功能厅 (容纳 350人) 北院多功能厅 (容纳160人) 北院多功能厅
(容纳160人)
主题 活动 A C B D
或
时间 星期一 星期二 星期三 星期四 星期五
地点 南院多功能厅 (容纳 350人) 北院多功能厅 (容纳 160人) 南院多功能厅 (容纳 350人) 北院多功能厅 (容纳160人) 北院多功能厅
(容纳160人)
主题 活动 B C A D
理由如下:根据统计图提供的信息,
参加主题活动A的学生人数约为 (人);
参加主题活动B的学生人数约为 (人);
参加主题活动的学生人数约为 (人);
所以主题活动 只能安排在南院多功能厅星期一进行;主题活动A和主题活
动B安排在北院多功能厅均可满足容纳人数的要求,星期二或星期四两天都
可以安排.
类型2 随机事件的概率
4.甲、乙两陌生人乘坐同一趟高铁列车从唐山前往北京.如图,网上购票时,购
票系统向两人都推送了第2车厢第13排的座位,其中座位D已有人预定,两人只
能在A,B,C, 四个座位选择一个座位,且选择这四个座位的可能性相同.
(1)求甲选择A座位的概率;
[答案] 由题意得甲可选择的座位有4个,且选择每个座位的可能性相同,
甲选择A座位的概率为 .
(2)用列表法或画树状图法求出甲、乙二人座位相邻的概率.
[答案] 根据题意,列表如下:
A B C
A
B
C
共有12种等可能的结果,甲、乙二人座位相邻的结果有4种,故所求概率
为 .
5.某超市为回馈广大消费者,在开业周年之际举行摸球抽奖活动.在一个不
透明的口袋中装有1个白球和2个红球,这些球除颜色外完全相同.
(1)从袋中随机摸出一个球,则摸出的这个球是红球的概率是__.
(2)活动设置了一等奖和二等奖两个奖项,一等奖的获奖率低于二等
奖.摸球规则如下:从袋中随机摸出一个球,不放回,再从袋中剩余的两个
球中随机摸出一个球.规定摸出颜色不同的两球和摸出颜色相同的两球分别
对应不同奖项,请写出它们分别对应的奖项,并说明理由.
[答案] 根据题意,画树状图如下.
由树状图可知,共有6种等可能的结果,其中摸出颜色不同的两球的结果有4种,
摸出颜色相同的两球的结果有2种,
摸出颜色不同的两球的概率为,摸出颜色相同的两球的概率为 .
一等奖的获奖率低于二等奖, ,
摸出颜色不同的两球对应的奖项为二等奖,摸出颜色相同的两球对应的奖
项为一等奖.
6.2024年巴黎奥运会新增霹雳舞、滑板、攀岩、冲浪四个项目.为了更好地观
赏这些项目,学校在四个场所开展了这四个项目的竞技知识讲座,要求每位学
生参与其中一场讲座.九(1)班在不透明的袋子中放置四个大小、质地一样
的小球,编号为1,2,3,4.
(1)若1号表示霹雳舞,2号表示滑板,3号表示攀岩,4号表示冲浪.第一位同学
从袋子中摸出一球,记录球号后放回袋子中,摇匀后让第二位同学摸出一
球……摸到球号是多少就去参加对应项目的讲座,求该班的小明和小华同学都
选中参加霹雳舞讲座的概率.
[答案] 根据题意画树状图如下:
由树状图可知,共有16种等可能的结果,其中两人都选中参加霹雳舞讲座的结
果有1种,所以小明和小华同学都选中参加霹雳舞讲座的概率是 .
(2)小明和小华同学都有霹雳舞基础,霹雳舞会场将从他们两人中选一人去
辅助教学.他俩都想去,于是商定:从袋子中一次性摸出两个球,若球号之和大于
5,则小明去辅助教学,否则小华去.他们商定的方案公平吗 若不公平,请修改游
戏规则使游戏公平.
[答案] 不公平.
理由:从袋子中随机摸出两球的结果有,,,,, ,
共6种等可能的结果,其中球号之和大于5的结果有2种, 小明去辅助教学的概
率为,而小华去辅助教学的概率为 .
, 他们商定的方案不公平.
游戏规则可以改为:从袋子中一次性摸出两个球,若球号之积大于5,则小明去
辅助教学,否则小华去.
类型3 统计与概率综合
7.某公司计划购入语音识别输入软件来提高办公效率.市面上有A,B两款语
音识别输入软件,该公司准备择优购买.为了解两款软件的性能,测试员小
敏随机选取了20个句子,其中每句都含10个字.她用标准普通话以相同的语
速朗读每个句子来测试这两款软件,并将语音识别结果进行了整理、描述和
分析,下面给出了部分信息:
A款软件每个句子中识别正确的 字数记录: 5,5,6,6,6, 6,6,6,7,7, 8,9,9,9,9, 10,10,10,10,10. B款软件每个句子中识别正确的字数的折
线统计图:
__________________________________________________
A,B两款软件每个句子中识别正确的字数的统计表如下.
软件 平均数 众数 中位数 识别正确达到10个字的句子所占百分比
A款 7.7 7.5
B款 7.7 8
根据以上信息.解答下列问题:
(1)上述表中的___,___, ______;
6
8
(2)若会议记录员用A,B两款软件各识别了500个句子,每个句子有10个
字,请估计两款软件一字不差地识别正确的句子共有多少个;
[答案] (个).
答:估计两款软件一字不差地识别正确的句子共有175个.
(3)该公司现派一个三人采购小组前去购进一批语音识别输入软件,若每
人从这两款软件中随机选择一款,求他们三人都选择A款软件的概率.
[答案] 将采购小组的三人分别记为甲、乙、丙.
根据题意,画树状图如下:
由树状图可知,共有8种等可能的结果,其中他们三人都选择A款软件的结果
有1种,所以他们三人都选择A款软件的概率是 .
同课章节目录
