【集中培优】浙江省杭州市近2年各区九年级上册期末考试压轴题集中训练卷 含解析
文档属性
| 名称 | 【集中培优】浙江省杭州市近2年各区九年级上册期末考试压轴题集中训练卷 含解析 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-12 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙江省杭州市近2年各区期末考试压轴题集中训练卷
一.选择题(共13小题)
1.(2023秋 上城区期末)已知二次函数y=a(x+m﹣1)(x﹣m)(a≠0)的图象上有两点A(x1,y1)和B(x2,y2)(其中x1<x2),则( )
A.若a>0,当x1+x2<1时,a(y1﹣y2)<0
B.若a>0,当x1+x2<1时,a(y1﹣y2)>0
C.若a<0,当x1+x2>﹣1时,a(y1﹣y2)<0
D.若a<0,当x1+x2>﹣1时,a(y1﹣y2)>0
2.(2023秋 西湖区期末)已知二次函数y=a(x﹣h)2+k(a≠0)的图象与一次函数y=px+q(p≠0)的图象交于(x1,y1)和(x2,y2)两点,则下列结论正确的是( )
A.若a>0,p<0,则x1+x2>2h
B.若x1+x2>2h,则a>0,p<0
C.若a<0,p<0,则x1+x2>2h
D.若x1+x2>2h,则a<0,p<0
3.(2023秋 拱墅区期末)如图,四边形ABCD内接于⊙O,其中AD>CD,已知对角线AC过点O,对角线BD与CO相交于点E,且AD=BD.若∠BDC=2∠DBC,则( )
A.1 B. C.2 D.3
4.(2023秋 滨江区期末)在平面直角坐标系中,已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0),当y≥t时,x≤m﹣1或x≥m+3.若该函数图象过点A(m,5)和B(m+4,q),则q的值可能是( )
A.3 B.4 C.5 D.6
5.(2023秋 拱墅区校级期末)如图,AB是⊙O的直径,点C,D在⊙O上,且∠OAC=30°,OD绕着点O顺时针旋转,连接CD交直线AB于点E,当DE=OD时,∠OCE的大小不可能为( )
A.20° B.40° C.70° D.80°
6.(2023秋 杭州期末)如图,正△ABC纸片,E为AC边上的一点,连结BE.将△BAE沿BE翻折得到△BFE,过点C作AB的平行线交EF的延长线于点M,若∠EMC=90° 则的比为( )
A. B. C. D.
7.(2023秋 杭州期末)如图,△ABC内接于⊙O,∠ABC>90°,它的外角∠EAC的平分线交⊙O于点D,连接DB,DC,DB交AC于点F.若DA=DF,∠ABC=α,∠DFC=β,则下列结论正确的是( )
A.α+4β=540° B.α+4β=450° C.α+2β=360° D.α+2β=270°
8.(2022秋 滨江区期末)二次函数y=ax2+4x+1(a为实数,且a<0),对于满足0≤x≤m的任意一个x的值,都有﹣2≤y≤2,则m的最大值为( )
A. B. C.2 D.
9.(2022秋 杭州期末)计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图:
当任务完成的百分比为x时,线段MN的长度记为d(x).下列描述正确的是( )
A.当x1>x2时,d(x1)>d(x2)
B.当d(x1)>d(x2)时,x1>x2
C.当x1+x2=1时,d(x1)=d(x2)
D.当x1=2x2时,d(x1)=2d(x2)
10.(2022秋 杭州期末)已知点P(m,n),Q(3,0)都在一次函数y=kx+b(k,b是常数,k≠0)的图象上,( )
A.若mn有最大值4,则k的值为﹣9
B.若mn有最小值4,则k的值为﹣9
C.若mn有最大值﹣9,则k的值为4
D.若mn有最小值﹣9,则k的值为4
11.(2022秋 上城区期末)如图,AD是△ABC的外角平分线,与△ABC的外接圆交于点D,连结BD交AC于点F,且BC=CF,则下列结论错误的是( )
A.∠ADB=∠CDB B.3∠ACB+∠ACD=180°
C.3∠BDC+2∠ABD=180° D.3∠BAD+∠ABD=360°
12.(2022秋 西湖区期末)设函数y1=﹣(x﹣a1)2,y2=﹣(x﹣a2)2.直线x=1的图象与函数y1,y2的图象分别交于点A(1,c1),B(1,c2),得( )
A.若1<a1<a2,则c1<c2 B.若a1<1<a2,则c1<c2
C.若a1<a2<1,则c1<c2 D.若a1<a2<1,则c2<c1
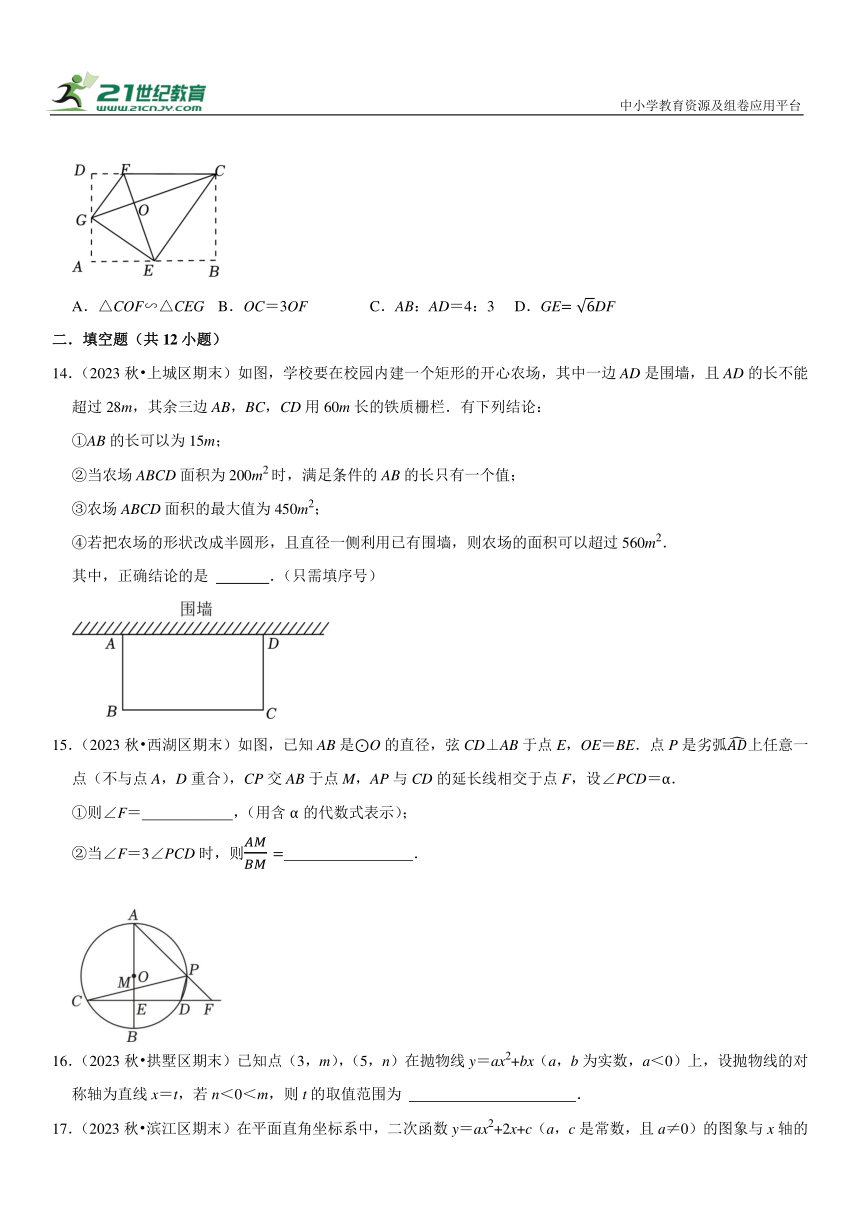
13.(2022秋 西湖区校级期末)如图,将矩形ABCD沿着GE,EC,GF翻折,使得点A,B,D恰好都落在点O处,且点G,O,C在同一条直线上,点E,O,F在另一条直线上.以下结论正确的是( )
A.△COF∽△CEG B.OC=3OF C.AB:AD=4:3 D.GEDF
二.填空题(共12小题)
14.(2023秋 上城区期末)如图,学校要在校园内建一个矩形的开心农场,其中一边AD是围墙,且AD的长不能超过28m,其余三边AB,BC,CD用60m长的铁质栅栏.有下列结论:
①AB的长可以为15m;
②当农场ABCD面积为200m2时,满足条件的AB的长只有一个值;
③农场ABCD面积的最大值为450m2;
④若把农场的形状改成半圆形,且直径一侧利用已有围墙,则农场的面积可以超过560m2.
其中,正确结论的是 .(只需填序号)
15.(2023秋 西湖区期末)如图,已知AB是⊙O的直径,弦CD⊥AB于点E,OE=BE.点P是劣弧上任意一点(不与点A,D重合),CP交AB于点M,AP与CD的延长线相交于点F,设∠PCD=α.
①则∠F= ,(用含α的代数式表示);
②当∠F=3∠PCD时,则 .
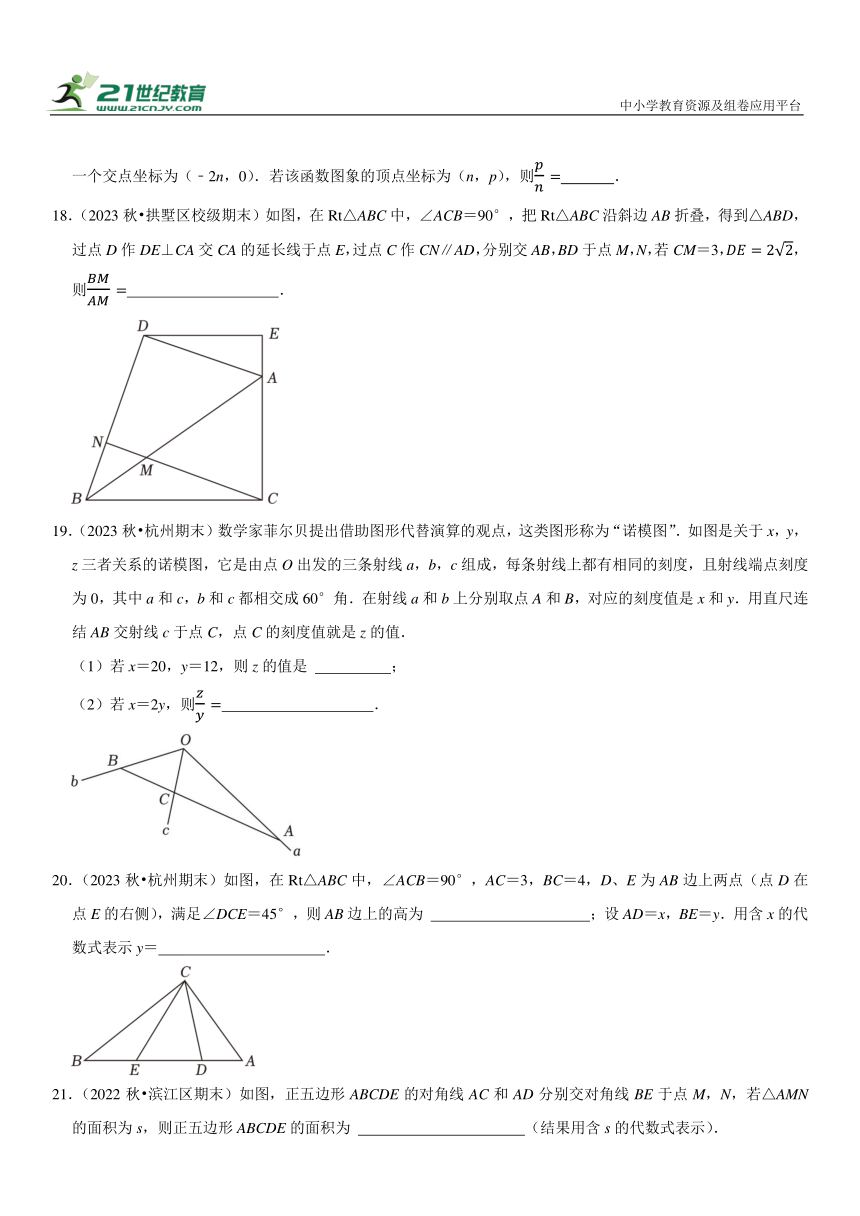
16.(2023秋 拱墅区期末)已知点(3,m),(5,n)在抛物线y=ax2+bx(a,b为实数,a<0)上,设抛物线的对称轴为直线x=t,若n<0<m,则t的取值范围为 .
17.(2023秋 滨江区期末)在平面直角坐标系中,二次函数y=ax2+2x+c(a,c是常数,且a≠0)的图象与x轴的一个交点坐标为(﹣2n,0).若该函数图象的顶点坐标为(n,p),则 .
18.(2023秋 拱墅区校级期末)如图,在Rt△ABC中,∠ACB=90°,把Rt△ABC沿斜边AB折叠,得到△ABD,过点D作DE⊥CA交CA的延长线于点E,过点C作CN∥AD,分别交AB,BD于点M,N,若CM=3,,则 .
19.(2023秋 杭州期末)数学家菲尔贝提出借助图形代替演算的观点,这类图形称为“诺模图”.如图是关于x,y,z三者关系的诺模图,它是由点O出发的三条射线a,b,c组成,每条射线上都有相同的刻度,且射线端点刻度为0,其中a和c,b和c都相交成60°角.在射线a和b上分别取点A和B,对应的刻度值是x和y.用直尺连结AB交射线c于点C,点C的刻度值就是z的值.
(1)若x=20,y=12,则z的值是 ;
(2)若x=2y,则 .
20.(2023秋 杭州期末)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,D、E为AB边上两点(点D在点E的右侧),满足∠DCE=45°,则AB边上的高为 ;设AD=x,BE=y.用含x的代数式表示y= .
21.(2022秋 滨江区期末)如图,正五边形ABCDE的对角线AC和AD分别交对角线BE于点M,N,若△AMN的面积为s,则正五边形ABCDE的面积为 (结果用含s的代数式表示).
22.(2022秋 杭州期末)如图,在正方形ABCD中,点E在边BC上(不与点B,C重合),点F在边CD的延长线上,DF=BE,连接EF交AD于点G,过点A作AN⊥EF于点M,交边CD于点N.若DN=2CN,BE=3.则CN= ,AM= .
23.(2022秋 上城区期末)如图,在矩形ABCD中,AD=4AB.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G,则 .
24.(2022秋 西湖区期末)如图,线段AB是⊙O的直径,弦CD⊥AB于点H,点M是弧BC上任意一点(不与B,C重合),AH=1,CH=2.延长线段BM交DC的延长线于点E,直线MH交⊙O于点N,连结BN交CE于点F,则OC= ,HE HF= .
25.(2022秋 西湖区校级期末)已知关于x的一元二次方程(x﹣2)(x﹣3)=m有实根x1,x2,且x1<x2,现有下列说法:①当m=0时,x1=2,x2=3;②当m>0时,2<x1<x2<3;③m;④二次函数y=(x﹣x1)(x﹣x2)﹣m的图象与x轴的交点坐标为(2,0)和(3,0).其中正确的有 .
三.解答题(共26小题)
26.(2023秋 上城区期末)如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.
(1)求证:△DOE∽△ABC;
(2)求证:∠ODF=∠BDE;
(3)连接OC,设△DOE的面积为S1,四边形OCBD的面积为S2,若,用含n的代数式表示.
27.(2023秋 西湖区期末)如图,E是正方形ABCD边BC上一个动点(不与B,C重合),F是CD延长线上一点,且DF=BE,连接AE,AF,EF.
(1)求证:△AEF为等腰直角三角形.
(2)过点A作EF的垂线,与直线EF,BC分别交于G,H两点,记∠DFE=α,EF交AD于点I.
①当α=30°,AI=2,求线段AE的长.
②设,△AGI的面积记作S1,△HGE的面积记作S2,用含k的代数式表示.
28.(2023秋 拱墅区期末)如图,四边形ABCD内接于⊙O,对角线AC平分∠BAD,连接BD交AC于点E.
(1)求证:△ABC∽△BEC.
(2)若AB=AC,设△ABD的面积为S1,△BCD的面积为S2,BE=6,EC=4,求的值.
(3)求证:AC2=BC2+AB AD.
29.(2023秋 滨江区期末)如图,在⊙O中,弦AB是直径,点C,D是⊙O上的两点,连结AC,OD,且满足AC∥OD.
(1)若的度数为80°,求∠A的度数.
(2)求证:.
(3)连结BD,若AC=6,AB=10,求BD的长.
30.(2023秋 拱墅区校级期末)如图,已知正方形ABCD的边长为12,点E是射线BC上一点(点E不与点B、C重合),过点A作AF⊥AE,交边CD的延长线于点F,直线EF分别交射线AC、射线AD于点M、N.
(1)求证:△ABE≌△ADF;
(2)当点E在边BC上时,如果AN=5DN,求∠BAE的正切值.
(3)当点E在边BC延长线上时,设线段BE=x,y=EN MF,求y关于x的函数解析式.
31.(2023秋 杭州期末)如图,⊙O是Rt△ABC的外接圆,点D是弧AB的中点,过点D作AB的平行线交CA的延长线于点E,连结BD,BE.
(1)求证:∠EDC=∠DBC;
(2)当CD=2时,求S△BCE的值;
(3)设BC=nAC.
①求的值;(用含n的代数式表示)
②若3CE=8AC,DE=6,求AB的长.
32.(2023秋 杭州期末)如图1,在△ABC中,AB=AC,∠A=90°,点P是△ABC内一个动点,且∠BPC=135°.
(1)试找出与∠ACP相等的角,并说明理由;
(2)如图2,连接AP并延长交△BPC的外接圆⊙O于点Q,交BC于点D,连接CQ.
①求证△ACP∽△AQC;
②求的最小值;
(3)在如图2的条件下,若BP=PC,求证:.
33.(2022秋 滨江区期末)如图1,在⊙O中,AB为弦,CD为直径,且AB⊥CD于点E,过点B作BF⊥AD,交AD的延长线于点F.连接AC,BO.
(1)求证:∠CAE=∠ADC.
(2)若DE=2OE,求的值.
(3)如图2,若BO的延长线与AC的交点G恰好为AC的中点,若⊙O的半径为r.求图中阴影部分的面积(结果用含r的代数式表示).
34.(2022秋 杭州期末)如图,⊙O的半径为1,直径AB,CD的夹角∠AOD=60°,点P是上一点,连接PA,PC分别交CD,AB于点M,N.
(1)若PC⊥AB,求证:PA⊥CD.
(2)当点P在上运动时,
①猜想:线段AM与CN有怎样的数量关系,并给出证明.
②求证:PA+PC.
35.(2022秋 杭州期末)如图,BD是矩形ABCD的对角线,,点E,F分别在边AD,BC上,把△ABE和△CDF分别沿直线BE,DF折叠,使点A,C分别落在对角线BD上的点G,H处,连接FG.
(1)求证:BH=DG.
(2)若AB=6,AD=8,求线段FG的长.
(3)若FG∥CD,求的值.
36.(2022秋 上城区期末)如图,E是矩形ABCD边BC上的一点,作DF⊥DE交BA的延长线于点F,连结EF交AD于点G.
(1)求证:△DCE∽△DAF;
(2)已知DC=1,BC=3,
①若G为AD中点,求FG:GE的值;
②若△DGE为等腰三角形,求CE的长.
37.(2022秋 西湖区期末)如图,△ABC内接于⊙O,∠ABC>90°,△ABC的外角∠EAC的平分线交⊙O于点D,连接DB,DC,DB交AC于点F.
(1)求证:△DBC是等腰三角形.
(2)若DA=DF.
①求证:BC2=DC BF.
②若⊙O的半径为5,BC=6,求的值.
38.(2022秋 西湖区校级期末)如图,AB、AC、AD是⊙O中的三条弦,点E在AD上,且AB=AC=AE.连结BC,BD,CD,其中BC交AD于点G.
(1)求证:△ABG∽△ADB.
(2)若∠DBE=α,求∠CAD的度数(用含α的代数式表示).
(3)若AD=15,AB=12,BD=6,求线段CD的长.
39.(2022秋 西湖区校级期末)已知二次函数y=ax2﹣2(a+1)x+4(a≠0).
(1)证明:二次函数的图象与x轴总有交点.
(2)若点P(,b)和点Q(n,b)在该二次函数图象上,求(b)2+n2的值.
(3)将该二次函数图象向下平移2个单位,令新函数图象与x轴的交点横坐标为x1,x2.证明:|x1﹣x2|>2.
40.(2022秋 西湖区期末)在直角坐标系中,设函数y=m(x+1)2+4n(m≠0,且m,n为实数),
(1)求函数图象的对称轴.
(2)若m,n异号,求证:函数y的图象与x轴有两个不同的交点.
(3)已知当x=0,3,4时,对应的函数值分别为p,q,r,若2q<p+r,求证:m<0.
41.(2022秋 上城区期末)二次函数y1=2(x﹣x1)(x﹣x2)(x1,x2是常数)的图象与x轴交于A,B两点.
(1)若A,B两点的坐标分别为(1,0),(2,0),求函数y1的表达式及其图象的对称轴;
(2)若函数y1的图象经过点(2,m),且x1+x2=2时,求m的最大值;
(3)若一次函数y2=kx+b(k,b是常数,k≠0),它的图象与y1的图象都经过x轴上同一点,且x1﹣x2=2.当函数y=y1+y2的图象与x轴仅有一个交点时,求k的值.
42.(2022秋 杭州期末)在平面直角坐标系中,点(1,m),(2,n)在函数y=x2+bx+c(b,c是常数)的图象上.
(1)若m=2,n=3,求该函数的表达式.
(2)若n=3m,求证:该函数的图象经过点.
(3)已知点(3,0),(﹣1,y1),(4,y2)在该函数图象上,若m>0,n<0,试比较y1,y2的大小,并说明理由.
43.(2022秋 杭州期末)已知二次函数y=ax2+bx+c(a>0)的图象经过点A(﹣1,1)和B(2,4).
(1)求a,b满足的关系式.
(2)当自变量x的值满足﹣1≤x≤2时,y随x的增大而增大,求a的取值范围.
(3)若函数图象与x轴无交点,求a2+b2的取值范围.
44.(2022秋 滨江区期末)二次函数y=x2﹣bx+c的图象经过(﹣2,y1),(1,y2)两点.
(1)当b=1时,判断y1与y2的大小.
(2)当y1<y2时,求b的取值范围.
(3)若此函数图象还经过点(m,y1),且1<b<2,求证:3<m<4.
45.(2023秋 杭州期末)综合与实践:问题情境:求方程x2+x﹣1=0的解,就是求二次函数y=x2+x﹣1的图象与x轴交点的横坐标.为了估计这个方程的解,圆圆先取了6个自变量满足x1<x2<x3<x4<x5<x6且x1﹣x2=x2﹣x3=x3﹣x4=x4﹣x5=x5﹣x6,再分别算出相应的y值.列表得:
x的值 x1 x2 x3 x4 x5 x6
y=x2+x﹣1的值 1 0.71 0.44 0.19 0.04 ﹣0.25
操作判断:(1)求x1的值;
实践探究:(2)为了分析函数值的变化规律,圆圆将表格中得到的函数值逐个作差.如:0.71﹣1=﹣0.29,0.44﹣0.71=﹣0.27,得到如下数据:﹣0.29,﹣0.27,﹣0.25,﹣0.15,﹣0.29,通过计算,圆圆发现自己由于粗心算错了其中的一个函数值,请指出算错的是哪一个值,正确的是多少?
问题解决:(3)对于一般的二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的函数值变化进行如表研究:(d≠0)
x的值 x x+d x+2d x+3d x+4d x+5d
y=ax2+bx+c的值 y1 y2 y3 y4 y5 y6
将表格中得到的函数值逐个作差,发现函数值的差与自变量满足某种函数关系,请写出你的发现过程以及发现结论.
46.(2023秋 杭州期末)已知二次函数y=ax2﹣2ax+1(a≠0),图象经过点(﹣1,m),(1,n),(3,p).
(1)当m=﹣2时.
①求二次函数的表达式;
②写出一个符合条件的x的取值范围,使得y随x的增大而增大;
(2)若在m,n,p这三个实数中,只有一个是正数,求证:.
47.(2023秋 拱墅区校级期末)已知二次函数y=x2﹣4x﹣5,点P1(x1,y1)与P2(x2,y2)都在该函数的图象上,且x1+x2=2.
(1)求函数图象的顶点;
(2)若点P1(x1,y1)与P2(x2,y2)与直线x=m的距离恒相等,求m的值;
(3)若y1≥y2,求y1的最小值.
48.(2023秋 滨江区期末)【综合与实践】
【认识研究对象】教材121页给出了如下定义:如图1,如果点P把线段AB分成两条线段AP和PB(AP>PB),且,则我们称点P为线段AB的黄金分割点.类似,我们可以定义:如果一个三角形中,其最长边的长度和最短边的长度的乘积等于第三边长度的平方,那么就称该三角形为“类黄金三角形”.
如图2,已知△ABC是“类黄金三角形”,且AC<AB<BC.若AC=3,BC=5,求AB的长.
【探索研究方法】如图3,已知△ABC是“类黄金三角形”,且AC<AB<BC.
若∠BAC=90°,小滨同学过点A作AD⊥BC于点D,发现了两个结论:
①AB2=BD×BC;
②点D是边BC的黄金分割点;
请给出证明.
【尝试问题解决】小滨同学经历以上探索过程发现:类似问题,可以通过构造相似三角形等方法解决.于是开展新的探究,请解决以下问题:
如图4,已知△ABC是“类黄金三角形”,且AC<AB<BC.若BC=2,∠A=90°∠C,求AB的长.
49.(2023秋 拱墅区期末)综合与实践:
问题背景:借助三角形的中位线可构造一组相似三角形,若将它们绕公共顶点旋转,对应顶点连线的长度存在特殊的数量关系,数学小组对此进行了研究.
如图1,在△ABC中,∠B=90°,AB=BC=4,分别取AB,AC的中点D,E,作△ADE.如图2所示,将△ADE绕点A逆时针旋转,连结BD,CE.
(1)探究发现
旋转过程中,线段BD和CE的长度存在怎样的数量关系?写出你的猜想,并证明.
(2)性质应用
如图3,当DE所在直线首次经过点B时,求CE的长.
(3)延伸思考
如图4,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,分别取AB,BC的中点D,E、作△BDE.将△BDE绕点B逆时针旋转,连接AD,CE.当边AB平分线段DE时,求tan∠ECB的值.
50.(2023秋 上城区期末)综合与实践
探究主题 直角三角板与圆
探究背景 学习了《圆周角》中的推论:“直径所对的圆周角等于90°”后,全班各研究小组用直角三角板开启了数学探究之旅——研究直角三角板的直角顶点在圆上、圆外和圆内三种情况(如图1),具体研究如图1.
探究任务1 找到画直径的简单方法:把直角顶点放在圆上,连接两直角边与圆的两个交点,连两交点的连线是直径.请你说出其中原理: .
探究任务2 用电脑作图工具,对直角顶点在圆外的情况进行动态模拟,发现:无论直角顶点在圆外如何运动,只要两直角边与圆有两个交点,两条直角边所夹的两段弧的度数差不变,为180°.如图2,若∠P=90°,则180°,研究小组对提出的结论进行证明: 证:如图3,连接AC ∵∠ACD,∠CAB, 又∵∠P=∠ACD﹣∠CAB=90°, ∴90°. ∴180°. 探究任务:运用以上研究结论,请用没有刻度的直尺,在图2的圆上截取一段弧等于,根据作图写出结论: .
探究任务3 当直角顶点运动到圆内时如图4,直角∠APD并反向延长两边交圆于B,C两点,形成互相垂直的弦.请观察图4类比探究任务2,对直角及其对顶角所对两段弧的数量关系,提出自己的猜想,并证明. 你的猜想: .(可以用文字描述,也可以结合图形用几何语言描述) 证明:…
探究任务4 各研究小组进行拓展研究比赛,其中高斯研究小组提出问题:如图5,若弦CD⊥AB,BP=3,DP=6,CP=2,求圆的直径. 比赛评分标准如表: 等级评价标准得分☆☆根据条件求出3条以上线段长,但没有求出直径2分☆☆☆☆根据条件求出直径,但没有运用以上探究结论4分☆☆☆☆☆创新运用探究任务4的结论,根据条件求出直径5分
你的解答是:…
51.(2023秋 西湖区期末)定义:由两条与x轴有相同的交点,并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”.
【概念理解】
抛物线y1=2(x﹣1)(x﹣2)与抛物线y2=x2﹣3x+2是否围成“月牙线”?说明理由.
【尝试应用】
抛物线y1(x﹣1)2﹣2与抛物线组成一个如图所示的“月牙线”,与x轴有相同的交点M,N(点M在点N的左侧),与y轴的交点分别为A,B.
①求a:b:c的值.
②已知点P(x0,m)和点Q(x0,n)在“月牙线”上,m>n,且m﹣n的值始终不大于2,求线段AB长的取值范围.
浙江省杭州市近2年各区期末考试压轴题集中训练卷
参考答案与试题解析
一.选择题(共13小题)
1.(2023秋 上城区期末)已知二次函数y=a(x+m﹣1)(x﹣m)(a≠0)的图象上有两点A(x1,y1)和B(x2,y2)(其中x1<x2),则( )
A.若a>0,当x1+x2<1时,a(y1﹣y2)<0
B.若a>0,当x1+x2<1时,a(y1﹣y2)>0
C.若a<0,当x1+x2>﹣1时,a(y1﹣y2)<0
D.若a<0,当x1+x2>﹣1时,a(y1﹣y2)>0
【分析】由二次函数的解析式求得对称轴为直线x,然后判断y1与y2的大小,即可判断每个选项正误.
【解答】解:∵二次函数y=a(x+m﹣1)(x﹣m)(a≠0),
∴y=0时,x1=1﹣m,x2=m,
∴二次函数y=a(x+m﹣1)(x﹣m)的对称轴为直线x,
当a>0时,当x1+x2<1时,
∴,
∴y1>y2,
∴y1﹣y2>0,
∴a(y1﹣y2)>0;
当a<0时,当x1+x2>﹣1时,
∴,
∴当时,y1<y2,
则a(y1﹣y2)>0;
当时,y1>y2,
则a(y1﹣y2)<0;
故选:B.
2.(2023秋 西湖区期末)已知二次函数y=a(x﹣h)2+k(a≠0)的图象与一次函数y=px+q(p≠0)的图象交于(x1,y1)和(x2,y2)两点,则下列结论正确的是( )
A.若a>0,p<0,则x1+x2>2h
B.若x1+x2>2h,则a>0,p<0
C.若a<0,p<0,则x1+x2>2h
D.若x1+x2>2h,则a<0,p<0
【分析】由二次函数解析式可得抛物线对称轴为直线x=h,由函数图象与系数的关系讨论(x1,y1)和(x2,y2)两点中x1+x2与2h的关系.
【解答】解:∵y=a(x﹣h)2+k,
∴抛物线对称轴为直线x=h,
∵a<0,p<0,
∴抛物线开口向下,一次函数中y随x增大而减小,
设x1<x2,则y1>y2,
∴h,
∴x1+x2>2h.
故选:C.
3.(2023秋 拱墅区期末)如图,四边形ABCD内接于⊙O,其中AD>CD,已知对角线AC过点O,对角线BD与CO相交于点E,且AD=BD.若∠BDC=2∠DBC,则( )
A.1 B. C.2 D.3
【分析】令∠DBC的度数为x,进一步表示出∠BDC、∠BAC和∠CAD的度数,利用等边对等角及直径所对的圆周角为90°,可求出x的值,进而发现△ABC是等腰直角三角形及AB与AE相等,即可解决问题.
【解答】解:令∠DBC的度数为x,则∠BDC的度数为2x,
∵,
∴∠BAC=∠BDC=2x,
∵,
∴∠CAD=∠CBD=x,
∴∠BAD=3x.
∵AD=BD,
∴∠DBA=∠DAB=3x.
∵AC为⊙O的直径,
∴∠ABC=90°,
则3x+x=90°,
解得x=22.5°.
∴∠BAC=∠BCA=45°,∠ABE=67.5°,
∴∠AEB=180°﹣45°﹣67.5°=67.5°,
∴AE=AB.
令⊙O的半径为R,
则AB2+CB2=(2R)2,
∵AB=CB,
∴AB,
∴AE=AB,
又∵CE=2R,
∴.
故选:A.
4.(2023秋 滨江区期末)在平面直角坐标系中,已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0),当y≥t时,x≤m﹣1或x≥m+3.若该函数图象过点A(m,5)和B(m+4,q),则q的值可能是( )
A.3 B.4 C.5 D.6
【分析】根据二次函数的性质得出抛物线的开口向上,对称轴为直线x=m+1,然后根据两点到对称轴的距离判断即可.
【解答】解:∵二次函数y=ax2+bx+c(a,b,c是常数,且a≠0),当y≥t时,x≤m﹣1或x≥m+3,
∴抛物线的开口向上,对称轴为直线xm+1,
∵该函数图象过点A(m,5)和B(m+4,q),且m+1﹣m<m+4﹣(m+1),
∴q>5,
故选:D.
5.(2023秋 拱墅区校级期末)如图,AB是⊙O的直径,点C,D在⊙O上,且∠OAC=30°,OD绕着点O顺时针旋转,连接CD交直线AB于点E,当DE=OD时,∠OCE的大小不可能为( )
A.20° B.40° C.70° D.80°
【分析】根据OD绕着点O顺时针旋转,连接CD交直线AB于点E,DE=OD,分三种情况画图进行计算即可.
【解答】解:
连接OC,
①如图1,OD绕着点O顺时针旋转,连接CD交直线AB于点E,
设∠OCE=x,
∵OC=OD,
∴∠OCE=∠D=x,
∵OA=OC,
∴∠OCA=∠A=30°,
∵DE=OD,
∴∠DOE=∠DEO=30°+x+30°=60°+x
∴2(60°+x)+x=180°
解得x=20°.
∴∠OCE的大小为20°;
②如图2,
设∠OEC=x,
∵DE=OD,
∴∠EOD=∠E=x,
∵DO=CO,
∴∠ODC=∠OCD=2x,
∠EOC=2∠A=60°
∴在△OCE中,
x+60°+2x=180°,
解得x=40°,
∴∠OCE=2x=80°;
③如图3,
设∠ACE=x,
∵OA=OC,
∴∠OCA=∠OAC=30°,
∵OC=OD,
∴∠OCD=∠ODC=30°+x,
∵OD=DE
∴∠EODC=15°x,
∴15°x+x=30°
解得x=10°,
∴∠OCE=30°+x=40°.
综上:∠OCE的大小为:20°、40°、80°.
故选:C.
6.(2023秋 杭州期末)如图,正△ABC纸片,E为AC边上的一点,连结BE.将△BAE沿BE翻折得到△BFE,过点C作AB的平行线交EF的延长线于点M,若∠EMC=90° 则的比为( )
A. B. C. D.
【分析】延长ME交AB于点G,设BF交AC于点H,由△ABC是正三角形得∠A=60°,由翻折得∠HFE=∠A=60°,FE=AE,因为CM∥AB,所以∠AGE=∠EMC=90°,可证明△FEH≌△AEG,得∠FHE=∠AGE=90°,则BF⊥AC,∠HEF=30°,则AH=CH,FE=AE=2FH,所以EHFH,可求得EC=(2+2)FH,即可求得,于是得到问题的答案.
【解答】解:延长ME交AB于点G,设BF交AC于点H,
∵△ABC是正三角形,
∴∠A=60°,
由翻折得∠HFE=∠A=60°,FE=AE,
∵CM∥AB,∠EMC=90°,
∴∠AGE=∠EMC=90°,
在△FEH和△AEG中,
,
∴△FEH≌△AEG(ASA),
∴∠FHE=∠AGE=90°,
∴BF⊥AC,∠HEF=90°﹣∠HFE=30°,
∴AH=CH,FE=AE=2FH,
∴EHFH,
∴AH=CH=AE+EH=2FHFH,
∴EC=CH+EH=2FHFHFH=(2+2)FH,
∴,
故选:D.
7.(2023秋 杭州期末)如图,△ABC内接于⊙O,∠ABC>90°,它的外角∠EAC的平分线交⊙O于点D,连接DB,DC,DB交AC于点F.若DA=DF,∠ABC=α,∠DFC=β,则下列结论正确的是( )
A.α+4β=540° B.α+4β=450° C.α+2β=360° D.α+2β=270°
【分析】由∠DAE+∠DAB=180°,∠DCB+∠DAB=180°,得∠DAE=∠DCB,所以∠DAE=∠DAC=∠DBC,则∠DAC=∠DBC=∠DCB,因为DA=DF,所以∠BFC=∠DFA=∠DAC=∠DBC=∠DCB,可证明△DAF∽△DBC,得∠ADB=∠BDC,再由∠ADB=∠ACB,∠BDC=∠BAC,推导出∠ACB=∠BAC,所以∠BDC=∠BAC(180°﹣α),则∠DBC=∠DCB(180°﹣∠BDC)=45°α,因为∠DFC=180°﹣∠BFC=180°﹣∠DBC=135°α,所以β=135°α,则α+4β=540°,可判断A正确,于是得到问题的答案.
【解答】解:∵∠DAE+∠DAB=180°,∠DCB+∠DAB=180°,
∴∠DAE=∠DCB,
∵AD平分∠EAC,
∴∠DAE=∠DAC=∠DBC,
∴∠DAC=∠DBC=∠DCB,
∵DA=DF,
∴∠BFC=∠DFA=∠DAC=∠DBC=∠DCB,
∵∠DAC=∠DBC,∠DFA=∠DCB,
∴△DAF∽△DBC,
∴∠ADB=∠BDC,
∴∠ADB=∠ACB,∠BDC=∠BAC,
∴∠ACB=∠BAC,
∵∠ABC=α,∠DFC=β,
∴∠BDC=∠BAC(180°﹣∠ABC)(180°﹣α),
∴∠DBC=∠DCB(180°﹣∠BDC)=90°(180°﹣α)=45°α,
∵∠DFC=180°﹣∠BFC=180°﹣∠DBC=180°﹣(45°α)=135°α,
∴β=135°α,
∴α+4β=540°,
故A正确,
故选:A.
8.(2022秋 滨江区期末)二次函数y=ax2+4x+1(a为实数,且a<0),对于满足0≤x≤m的任意一个x的值,都有﹣2≤y≤2,则m的最大值为( )
A. B. C.2 D.
【分析】由该二次函数解析式可知,该函数图象的开口方向向下,对称轴为,该函数的最大值为,由题意可解得a≤﹣4,根据函数图象可知a的值越小,其对称轴越靠左,满足y≥﹣2的x的值越小,故令a=﹣4即可求得m的最大值.
【解答】解:∵函数,且a<0,
∴该函数图象的开口方向向下,对称轴为,该函数有最大值,其最大值为,
若要满足0≤x≤m的任意一个x的值,都有﹣2≤y≤2,
则有,解得a≤﹣4,
对于该函数图象的对称轴,a的值越小,其对称轴越靠左,
a的值越小,满足y≥﹣2的x的值越小,
∴当取a的最大值,即a=﹣4时,令y=﹣4x2+4x+1=﹣2,
解得,,
∴满足y≥﹣2的x的最大值为,
即m的最大值为.
故选:D.
9.(2022秋 杭州期末)计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图:
当任务完成的百分比为x时,线段MN的长度记为d(x).下列描述正确的是( )
A.当x1>x2时,d(x1)>d(x2)
B.当d(x1)>d(x2)时,x1>x2
C.当x1+x2=1时,d(x1)=d(x2)
D.当x1=2x2时,d(x1)=2d(x2)
【分析】根据弧,弦和圆心角的关系,利用图象判断即可.
【解答】解:A、当x1>x2时,d(x1)与d(x2)可能相等,可能不等,本选项不符合题意.
B、当d(x1)>d(x2)时,x1>x2或x1<x2,本选项不符合题意.
A、当x1+x2=1时,d(x1)=d(x2),正确,本选项符合题意.
D、当x1=2x2时,d(x1)<2 d(x2)本选项不符合题意.
故选:C.
10.(2022秋 杭州期末)已知点P(m,n),Q(3,0)都在一次函数y=kx+b(k,b是常数,k≠0)的图象上,( )
A.若mn有最大值4,则k的值为﹣9
B.若mn有最小值4,则k的值为﹣9
C.若mn有最大值﹣9,则k的值为4
D.若mn有最小值﹣9,则k的值为4
【分析】由题意得到mn=m(km﹣3k)=k(m2﹣3m)=kk,当k>0mn有最小值,求出k的值,当k<0,mn有最大值,求出k的值,即可解决问题.
【解答】解:∵点P(m,n),Q(3,0)都在一次函数y=kx+b(k,b是常数,k≠0)的图象上,
∴km+b=n,3k+b=0,
∴b=﹣3k,
∴n=km+b=km﹣3k,
∴mn=m(km﹣3k)=k(m2﹣3m)=kk,
当k<0时,mn有最大值k,
若mn有最大值4,k=4,则k,故A不符合题意;
若mn有最大值﹣9,k=﹣9,则k=4,此时k>0,故C不符合题意;
当k>0时,mn有最小值k,
若mn有最小值4,k=4,则k,故B不符合题意;
若mn有最小值﹣9,k=﹣9,则k=4,故D符合题意.
故选:D.
11.(2022秋 上城区期末)如图,AD是△ABC的外角平分线,与△ABC的外接圆交于点D,连结BD交AC于点F,且BC=CF,则下列结论错误的是( )
A.∠ADB=∠CDB B.3∠ACB+∠ACD=180°
C.3∠BDC+2∠ABD=180° D.3∠BAD+∠ABD=360°
【分析】设∠DCB=α,∠BDC=β,表示出有关的角,由圆周角定理,圆内接四边形的性质,可以解决问题.
【解答】解:AD是△ABC的外角平分线,
∴∠EAD=∠DAC,
∵∠EAD=∠DCB,∠DAC=∠DBC,
∴∠DBC=∠DCB,
∵BC=CF,
∴∠FBC=∠CFB,
∴∠BDC=∠BCF,
∵∠ADB=∠BCF,
∴∠ADB=∠BDC.
故A正确,
设∠DCB=α,∠BDC=β,则∠ADB=∠ACB=β,
∴2α+β=180°,
∴3∠ACB+∠ACD=3β+(α﹣β)=α+2β≠180°,
故B错误;
3∠BDC+2∠ABD=3β+2∠ACD=3β+2(α﹣β)=2α+β=180°,
故C正确;
3∠BAD+∠ABD=3(180°﹣α)+(α﹣β)=540°﹣(2α+β)=540°﹣180°=360°,
故D正确;
故选:B.
12.(2022秋 西湖区期末)设函数y1=﹣(x﹣a1)2,y2=﹣(x﹣a2)2.直线x=1的图象与函数y1,y2的图象分别交于点A(1,c1),B(1,c2),得( )
A.若1<a1<a2,则c1<c2 B.若a1<1<a2,则c1<c2
C.若a1<a2<1,则c1<c2 D.若a1<a2<1,则c2<c1
【分析】根据题意分别画出y1,y2的图象,继而根据图象即可求解.
【解答】解:∵直线x=1的图象与函数y1,y2的图象分别交于点A(1,c1),B(1,c2),
A.若1<a1<a2,如图所示,
则c1>c2
B.若a1<1<a2,如图所示,
则c1>c2
则c1<c2,
故B选项不合题意,
C.若a1<a2<1,如图所示,
∴c1<c2,故C选项正确,D选项不正确;
故选:C.
13.(2022秋 西湖区校级期末)如图,将矩形ABCD沿着GE,EC,GF翻折,使得点A,B,D恰好都落在点O处,且点G,O,C在同一条直线上,点E,O,F在另一条直线上.以下结论正确的是( )
A.△COF∽△CEG B.OC=3OF C.AB:AD=4:3 D.GEDF
【分析】先证明GF∥CE,再根据平行线的性质与相似三角形的性质可得FG=FC,可判断A.由矩形的性质设AD=BC=2a,AB=DC=2b,可得,可得,可判断C,设OF=DF=x,可得:,从而可判断D,B,从而可得答案.
【解答】解:由折叠性质可得:DG=OG=AG,AE=OE=BE,OC=BC,∠DGF=∠OGF,∠AGE=∠OGE,∠AEG=∠OEG,∠OEC=∠BEC,
∴∠FGE=∠FGO+∠OGE=90°,∠GEC=∠OEG+∠OEC=90°,
∴∠FGE+∠GEC=180°,
∴GF∥CE,
∴∠FGC=∠GCE,
若△COF∽△CEG,则∠FCO=∠GCE,
∴∠FGC=∠FCO,
∴FG=FC,与题干条件矛盾,故A不符合题意;
由矩形的性质设AD=BC=2a,AB=DC=2b,
由对折可得DG=OG=AG=a,AE=OE=BE=b,
∴CG=OG+OC=OG+BC=3a,
在Rt△CGE中,CG2=GE2+CE2,
∴(3a)2=a2+b2+b2+(2a)2,
解得:,
∴;
∴,故C不符合题意;
在Rt△COF中,设OF=DF=x,
则,
由∠D=∠GOF=90°,
∴,
解得:,
∴,,
在Rt△AGE中,,
∴,故D符合题意;
∴,故B不符合题意;
故选:D.
二.填空题(共12小题)
14.(2023秋 上城区期末)如图,学校要在校园内建一个矩形的开心农场,其中一边AD是围墙,且AD的长不能超过28m,其余三边AB,BC,CD用60m长的铁质栅栏.有下列结论:
①AB的长可以为15m;
②当农场ABCD面积为200m2时,满足条件的AB的长只有一个值;
③农场ABCD面积的最大值为450m2;
④若把农场的形状改成半圆形,且直径一侧利用已有围墙,则农场的面积可以超过560m2.
其中,正确结论的是 ② .(只需填序号)
【分析】依据题意,设AD边长为x m,则AB边长为长为m,当AB=15时,15,解得x=30,故可判断①;当菜园ABCD面积为200m2,由题意得x 200,从而x=30±10,又x≤28,故可判断②;又设矩形菜园的面积为y m2,从而y=x (x﹣30)2+450,结合0,x≤28,从而当x=28时,y有最大值,最大值为448m2不可能为450m2,故可判断③;依据题意,直径一侧是围墙,当直径取最大值28时,半圆的弧长为π×28<60,进而设沿AD方向栅栏延伸a米,则π(28+a)=60﹣a.求得a≈6.2,最后得农场的最大面积为π()2≈459.1<560,故可判断④.
【解答】解:设AD边长为x m,则AB边长为长为m,
当AB=15时,15,
解得x=30,
∵AD的长不能超过28m,
∴x≤28,
故①不正确.
∵菜园ABCD面积为200m2,
∴x 200.
∴x=30±10.
又x≤28,
∴x=30﹣10.
∴满足条件的AB的长只有一个值,故②正确.
由题意,设矩形菜园的面积为y m2,
根据题意得:y=x (x﹣30)2+450,
∵0,x≤28,
∴当x=28时,y有最大值,最大值为448m2不可能为450m2.
故③不正确.
∵直径一侧是围墙,当直径取最大值28时,半圆的弧长为π×28<60,
∴设沿AD方向栅栏延伸a米,则π(28+a)=60﹣a.
∴a≈6.2.
∴农场的最大面积为π()2≈459.1<560.
∴农场的面积不超过560m2.
故④错误.
故答案为:②.
15.(2023秋 西湖区期末)如图,已知AB是⊙O的直径,弦CD⊥AB于点E,OE=BE.点P是劣弧上任意一点(不与点A,D重合),CP交AB于点M,AP与CD的延长线相交于点F,设∠PCD=α.
①则∠F= 60°﹣α ,(用含α的代数式表示);
②当∠F=3∠PCD时,则 .
【分析】①连接OD,BD,PO,由线段垂直平分线的性质得到△ODB是等边三角形,由圆周角定理得到∠A∠POB=30°+α,由直角三角形的性质即可求出∠PFE=60°﹣α.
②设圆的半径是r,OM=x,由∠AFE=3∠PCD,求出α=15°,得到∠POB=90°,因此OP∥CE,推出△POM∽△CEM,得到OM:EM=OP:CE,代入有关数据即可求出OM的长,得到AM,BM的长,即可得到答案.
【解答】解:①连接OD,BD,PO,
∵弦CD⊥AB于点E,OE=BE,
∴OD=BD,
∵OD=OB,
∴△ODB是等边三角形,
∴∠BOD=60°,
∵∠PCD=α,
∴∠POD=2α,
∴∠POB=60°+2α,
∴∠A∠POB=30°+α,
∴∠PFE=90°﹣∠A=60°﹣α.
故答案为:60°﹣α;
②∵∠AFE=3∠PCD,
∴60°﹣α=3α,
∴α=15°,
∴∠POD=2∠PCD=30°,
∴∠POB=90°,
∴OP∥CE,
∴△POM∽△CEM,
∴OM:EM=OP:CE,
∵直径AB⊥CD,
∴DE=CE,
∴OM:EM=OP:ED,
设圆的半径是r,OM=x,
∴EMr﹣x,DEr,
∴x:(r﹣x)=r:r,
∴x=(2)r,
∴OM=(2)r,
∴AM=AO+OM=3rr,BM=OB﹣OMr﹣r,
∴.
故答案为:.
16.(2023秋 拱墅区期末)已知点(3,m),(5,n)在抛物线y=ax2+bx(a,b为实数,a<0)上,设抛物线的对称轴为直线x=t,若n<0<m,则t的取值范围为 t .
【分析】先根据题意得出抛物线与x轴的交点坐标,再由n<0<m即可得出结论.
【解答】解:由题意可知,抛物线与x轴的交点坐标为(0,0),(2t,0),
∵a<0,
∴抛物线开口向下,
∵点(3,m),(5,n)在抛物线y=ax2+bx(a,b为实数,a<0)上,n<0<m,
∴3<2t<5,
∴t.
故答案为:t.
17.(2023秋 滨江区期末)在平面直角坐标系中,二次函数y=ax2+2x+c(a,c是常数,且a≠0)的图象与x轴的一个交点坐标为(﹣2n,0).若该函数图象的顶点坐标为(n,p),则 9 .
【分析】根据抛物线的对称性求得二次函数y=ax2+2x+c(a,c是常数,且a≠0)的图象与x轴的另一个交点坐标为(4n,0),则y=a(x+2n)(x﹣4n)=a(x﹣n)2﹣9an2,由该函数图象的顶点坐标为(n,p)可知n,p=﹣9an2,代入求得即可.
【解答】解:∵函数图象的顶点坐标为(n,p),
∴对称轴为直线x=n,
∵二次函数y=ax2+2x+c(a,c是常数,且a≠0)的图象与x轴的一个交点坐标为(﹣2n,0).
∴二次函数y=ax2+2x+c(a,c是常数,且a≠0)的图象与x轴的另一个交点坐标为(4n,0).
∴y=a(x+2n)(x﹣4n)=a(x﹣n)2﹣9an2,
∴p=﹣9an2,
∴9an,
∴n,
∴9,
故答案为:9.
18.(2023秋 拱墅区校级期末)如图,在Rt△ABC中,∠ACB=90°,把Rt△ABC沿斜边AB折叠,得到△ABD,过点D作DE⊥CA交CA的延长线于点E,过点C作CN∥AD,分别交AB,BD于点M,N,若CM=3,,则 .
【分析】连接DM并延长交BC于点F,首先证明四边形ACMD为平行四边形,AD=CM=3,再证明四边形DFCE为矩形,用勾股定理计算出FM=1,由折叠图形性质、平行线性质及角平分线性质定理可得NM=FM=1,最后证明△BNM∽△BDA,然后根据相似三角形的性质求解.
【解答】解:如图所示,连接DM并延长交BC于点F,
∵CM∥AD,
∴∠DAM=∠CMA,
又由折叠性质可得CA=AD,∠DAM=∠CAM,
∴∠CAM=∠CMA,
∴CA=CM,
∴CM=AD,
∴四边形ACMD为平行四边形,AD=CM=3,
∴DM∥EC,DF∥EC,
又∵∠ECB=90°,
∴∠DFC=90°,
又∵∠E=90°,
∴四边形DFCE为矩形.
∴DE=FC=2,
∴FM1,
由折叠性质可得∠ADB=∠ACB=90°,
又CM∥AD,
∴∠BNM=∠ADB=90°.
又MF⊥BC,BA为∠DBC的角平分线,
∴NM=FM=1,
由MN∥AD,
∴△BNM∽△BDA,
∴,
设BM=k,BA=3k,则AM=3k﹣k=2k,
∴.
故答案为:.
19.(2023秋 杭州期末)数学家菲尔贝提出借助图形代替演算的观点,这类图形称为“诺模图”.如图是关于x,y,z三者关系的诺模图,它是由点O出发的三条射线a,b,c组成,每条射线上都有相同的刻度,且射线端点刻度为0,其中a和c,b和c都相交成60°角.在射线a和b上分别取点A和B,对应的刻度值是x和y.用直尺连结AB交射线c于点C,点C的刻度值就是z的值.
(1)若x=20,y=12,则z的值是 7.5 ;
(2)若x=2y,则 .
【分析】方法一(利用相似三角形):过点C作CD∥OB交OA于点D,先证△OCD为等边三角形得CD=OD=OC=z,进而得AD=x﹣z,再证△ACD和△ABO相似得AD:OA=CD:OB,由此得(x﹣z):x=z:y,然后整理得xz+yz=xy.
(1)将x=20,y=12代入xz+yz=xy之中即可求出z的值;
(2)将x=2y代入xz+yz=xy之中即可求出的值.
解法二(面积法):过点C作CE⊥OA于E,OF⊥OB于F,过B作BH⊥AO交AO的延长线于H,利用三角函数分别求出CE,CF,BH,进而可得S△AOC,S△BOC,S△AOB,然后根据S△AOC+S△BOC=S△AOB,得xz+yz=xy.
(1)将x=20,y=12代入xz+yz=xy之中即可求出z的值;
(2)将x=2y代入xz+yz=xy之中即可求出的值.
【解答】解法一(利用相似三角形):过点C作CD∥OB交OA于点D,如图1所示:
依题意得:∠BOC=∠AOC=60°,OA=x,OB=y,OC=z,
∵CD∥OB,
∴∠OCD=∠BOC=60°,
∴∠OCD=∠AOC=60°,
∴△OCD为等边三角形,
∴CD=OD=OC=z,
∴AD=OA﹣OD=x﹣z,
∵CD∥OB,
∴△ACD∽△ABO,
∴AD:OA=CD:OB,
∴(x﹣z):x=z:y,
整理得:xz+yz=xy,
(1)当x=20,y=12时,20z+12z=20×12,
解得:z=7.5;
故答案为:7.5.
(2)当x=2y时,2yz+yz=2y2,
即3yz=2y2,
∵y≠0,
∴3z=2y,
∴.
故答案为:.
解法二(面积法):过点C作CE⊥OA于E,OF⊥OB于F,过B作BH⊥AO交AO的延长线于H,如图2所示:
依题意得:∠BOC=∠AOC=60°,OA=x,OB=y,OC=z,
在Rt△OCE中,sin∠AOC,
∴CE=OC sin∠AOC=z sin60°,
在Rt△OCF中,sin∠BOC,
∴CF=OC sin∠BOC=z sin60°,
∵∠BOC=∠AOC=60°,
∴∠AOB=120°,
∴∠BOH=180°﹣∠AOB=60°,
在Rt△BOH中,sin∠BOH,
∴BH=OB sin∠BOH=y sin60°,
∴S△AOCOA CE,S△BOCOB CF,S△AOBOA BH,
∵S△AOC+S△BOC=S△AOB,
∴,
∴xz+yz=xy,
(1)当x=20,y=12时,20z+12z=20×12,
z=7.5;
故答案为:7.5.
(2)当x=2y时,2yz+yz=2y2,
即3yz=2y2,
∵y≠0,
∴3z=2y,
∴.
故答案为:.
20.(2023秋 杭州期末)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,D、E为AB边上两点(点D在点E的右侧),满足∠DCE=45°,则AB边上的高为 ;设AD=x,BE=y.用含x的代数式表示y= .
【分析】利用面积法可求出AB边上的高,旋转△ACD,利用“角含半角”模型构造出全等三角形,再借助于勾股定理即可解决问题.
【解答】解:过点C作AB的垂线,垂足为M,
∵∠ACB=90°,AC=3,BC=4,
∴AB.
又∵,
∴.
即AB边上的高为.
将△ACD绕点C顺时针旋转90°,点A的对应点为点F,点D的对应点为H,延长HF交AB于点G,连接EH,
由旋转可知,
△CHF≌△CDA,
∴∠HCF=∠DCA,HF=AD=x,CF=AC=3,∠HFC=∠A,CH=CD.
又∵∠HFC=∠BFG,∠A+∠B=90°,
∴∠B+∠BFG=90°,
则FG⊥BE.
又∵BF=4﹣3=1.
∴sinB,
则FG.
同理可得,BG.
∴HG=x,EG=y.
∵∠DCE=45°,
∴∠ACD+∠BCE=45°,
∴∠HCE=∠HCF+∠BCE=45°,
∴∠HCE=∠DCE.
在△HCE和△DCE中,
,
∴△HCE≌△DCE(SAS),
∴HE=DE=5﹣x﹣y.
在Rt△HGE中,
(x)2+(y)2=(5﹣x﹣y)2,
整理得,
y.
故答案为:,.
21.(2022秋 滨江区期末)如图,正五边形ABCDE的对角线AC和AD分别交对角线BE于点M,N,若△AMN的面积为s,则正五边形ABCDE的面积为 (结果用含s的代数式表示).
【分析】由正五边形的性质可得,△AMN∽△BAN∽△ACD,设AB=a,表示出解得AMa,则MN=aaa,得出S△ABMs,同理求出S△ACDs,从而解决问题.
【解答】解:由正五边形的性质可知,AB=BC=CD=DE=AE,AM=AN=BM=NE,
由正五边形的性质可得,△AMN∽△BAN∽△ACD,
设AB=a,
∵△AMN∽△BAN,
∴,
即,
解得AMa,
∴MN=aaa,
∴,
∴S△ABMs,
∵△AMN∽△ACD,
∴()2,
∴S△ACDs,
∴S正五边形ABCDE=S△ACD+4S△ABM+2S△AMN
s+4s+2s
,
故答案为:.
22.(2022秋 杭州期末)如图,在正方形ABCD中,点E在边BC上(不与点B,C重合),点F在边CD的延长线上,DF=BE,连接EF交AD于点G,过点A作AN⊥EF于点M,交边CD于点N.若DN=2CN,BE=3.则CN= 5 ,AM= 3 .
【分析】连接AE,AF,EN,由正方形的性质可得AB=AD,BC=CD,∠ABE=∠BCD=∠ADF=90°,可证得△ABE≌△ADF(SAS),可得∠BAE=∠DAF,AE=AF,从而可得∠EAF=90°,根据等腰三角形三线合一可得点M为EF中点,由AN⊥EF可证得△AEM≌△AFM(SAS),△EMN≌△FMN(SAS),可得EN=FN,设CN=x,构建方程求解.
【解答】解:如图,连接AE,AF,EN,
∵四边形ABCD为正方形,
∴AB=AD,BC=CD,∠ABE=∠BCD=∠ADF=90°,
∵BE=DF,
∴△ABE≌△ADF(SAS),
∴∠BAE=∠DAF,AE=AF,
∴∠EAF=90°,
∴△EAF为等腰直角三角形,
∵AN⊥EF,
∴EM=FM,∠EAM=∠FAM=45°,
∴△AEM≌△AFM(SAS),△EMN≌△FMN(SAS),
∴EN=FN,
设CN=x,则DN=2x,BC=CD=3x,
∴EN=FN=DN+DF=2x+3,CE=BC﹣BE=3x﹣3,
在Rt△ECN中,由勾股定理可得:
CN2+CE2=EN2,
即x2+(3x﹣3)2=(2x+3)2,
解得x=5,
∴CN=5,EC=12,CF=18,
∴EF6,
∴AMEF=3.
故答案为:5,3.
23.(2022秋 上城区期末)如图,在矩形ABCD中,AD=4AB.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G,则 .
【分析】由矩形及折叠的性质得∠MNC=∠PNM=90°,CN=DM=2DC=2MN,由∠PME∠AME,∠CME∠DME,可推导出∠PMC=90°,则∠MCN=∠PMN=90°﹣∠CMN,即可证明△MNC∽△PNM,得2,即可证明PNPC,再证明∠FMP=∠AMP=∠FPM,∠FMC=∠DMC=∠FCM,则PF=MF=CFPC,所以NF=PF﹣PNPC,即可求得.
【解答】解:∵四边形ABCD是矩形,
∴AB=DC,∠D=∠DCN=90°,AD∥BC,
∴AD=4AB=4DC,
∵将矩形ABCD对折,得到折痕MN,
∴DM=AMAD4DC=2DC,∠MNC=∠PNM=90°,
∴四边形CDMN是矩形,
∴DC=MN,
∴CN=DM=2DC=2MN,
∴∠PME=∠PMA∠AME,∠CME=∠CMD∠DME,
∴∠PMC=∠PME+∠CME(∠AME+∠DME)180°=90°,
∴∠MCN=∠PMN=90°﹣∠CMN,
∴△MNC∽△PNM,
∴2,
∴MN=2PN,CN=2MN,
∴CN=4PN,
∴PNPC,
∵∠FMP=∠AMP=∠FPM,∠FMC=∠DMC=∠FCM,
∴PF=MF=CFPC,
∴NF=PF﹣PNPCPCPC,
∴,
故答案为:.
24.(2022秋 西湖区期末)如图,线段AB是⊙O的直径,弦CD⊥AB于点H,点M是弧BC上任意一点(不与B,C重合),AH=1,CH=2.延长线段BM交DC的延长线于点E,直线MH交⊙O于点N,连结BN交CE于点F,则OC= 2.5 ,HE HF= 4 .
【分析】连接OC,设OC=r,在Rt△COH中,利用勾股定理求出OC;由△EHM∽△NHF,推出,推出HE HF=HM HN,又HM HN=AH HB,推出HE HF=AH HB,由此即可解决问题.
【解答】解:连接OC.
∵CD⊥AB,
∴∠CHO=90°,
设OC=r,则OH=r﹣1,
在Rt△COH中,
∵CH=2,
∴r2=22+(r﹣1)2,
∴r=2.5,即OC=2.5;
连接AM.
∵AB是直径,
∴∠AMB=90°,
∴∠MAB+∠ABM=90°,
∵∠E+∠ABM=90°,
∴∠E=∠MAB,
∴∠MAB=∠MNB=∠E,
∵∠EHM=∠NHF,
∴△EHM∽△NHF,
∴,
∴HE HF=HM HN,
∵HM HN=AH HB,
∴HE HF=AH HB=1×(5﹣1)=4,
故答案为:2.5,4.
25.(2022秋 西湖区校级期末)已知关于x的一元二次方程(x﹣2)(x﹣3)=m有实根x1,x2,且x1<x2,现有下列说法:①当m=0时,x1=2,x2=3;②当m>0时,2<x1<x2<3;③m;④二次函数y=(x﹣x1)(x﹣x2)﹣m的图象与x轴的交点坐标为(2,0)和(3,0).其中正确的有 ①③ .
【分析】解一元二次方程(x﹣2)(x﹣3)=0,根据一元二次方程根与系数的关系即可求解.
【解答】解:①当m=0时,一元二次方程为(x﹣2)(x﹣3)=0,
∴x1=2,x2=3,故①正确;
②当m>0时,
∵一元二次方程(x﹣2)(x﹣3)=m有实根x1,x2,且x1<x2,
∴原方程转化为x2﹣5x+6﹣m=0,
根据根与系数的关系得,,,
若2<x1<x2<3,则|x2﹣x1|<1,
∵,且m>0,
∴|x2﹣x1|<1错误,即2<x1<x2<3错误,故②错误;
∴当m>0时,x<2或x>3,故②错误;
③(x﹣2)(x﹣3)=m转化为x2﹣5x+6﹣m=0,有实根x1,x2,且x1<x2,
∴Δ=b2﹣4ac=(﹣5)2﹣4(6﹣m)>0,即1+4m>0,
∴,故③正确;
④∵一元二次方程(x﹣2)(x﹣3)=m有实根x1,x2,且x1<x2,
∴原方程转化为x2﹣5x+6﹣m=0,
根据根与系数的关系得,,,
∴,即y=x2﹣5x+6﹣2m,
∴由二次函数y=(x﹣x1)(x﹣x2)﹣m的图象与x轴的交点坐标不是(2,0)和(3,0),故④错误.
综上所述,正确的有①③,
故答案为:①③.
三.解答题(共26小题)
26.(2023秋 上城区期末)如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.
(1)求证:△DOE∽△ABC;
(2)求证:∠ODF=∠BDE;
(3)连接OC,设△DOE的面积为S1,四边形OCBD的面积为S2,若,用含n的代数式表示.
【分析】(1)根据圆周角定理和垂直求出∠DEO=∠ACB,根据平行得出∠DOE=∠ABC,根据相似三角形的判定得△DOE∽△ABC,根据圆周角定理得出∠A=∠BDC,推出∠ODE=∠BDC即可;
(2)根据圆周角定理和垂直求出∠DEO=∠ACB,根据平行得出∠DOE=∠ABC,根据相似三角形的判定得出结论;
(3)根据△DOE∽△ABC,求出S△ABC=4S△DOE=4S1,进而求解.
【解答】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD∥BC,
∴∠DOE=∠ABC,
∴△DOE∽△ABC;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD∥BC,
∴∠DOE=∠ABC,
∴△DOE∽△ABC;
∴∠ODE=∠A,
∵∠A和∠BDC是所对的圆周角,
∴∠A=∠BDC,
∴∠ODE=∠BDC,
∴∠ODF=∠BDE;
(3)解:∵△DOE∽△ABC,
∴()2,
即S△ABC=4S△DOE=4S1,
∵OA=OB,
∴S△BOCS△ABC,即S△BOC=2S1,
∵,S2=S△BOC+S△DOE+S△DBE=2S1+S1+S△DBE,
∴S△DBES1,
∴BE=()OE,
即OEOBDO,
∴sinA=sin∠ODE.
27.(2023秋 西湖区期末)如图,E是正方形ABCD边BC上一个动点(不与B,C重合),F是CD延长线上一点,且DF=BE,连接AE,AF,EF.
(1)求证:△AEF为等腰直角三角形.
(2)过点A作EF的垂线,与直线EF,BC分别交于G,H两点,记∠DFE=α,EF交AD于点I.
①当α=30°,AI=2,求线段AE的长.
②设,△AGI的面积记作S1,△HGE的面积记作S2,用含k的代数式表示.
【分析】(1)证明Rt△ADF≌△ABE,从而∠DAF=∠BAE,AF=AE,进一步得出结论;
(2)①可得出∠GAI=∠DFE=30°,解直角三角形AGI求得AG,解直角三角形AGF求得AF,进而得出AE;
②根据tan∠GAI=tan∠DFE得出,进而得出,可证得△AGI∽△HGE,进而求得结果.
【解答】(1)证明:∵正方形ABCD边,
∴AD=AB,∠ADF=∠ADC=∠B=90°,
∵DF=BE,
∴Rt△ADF≌△ABE(HL),
∴∠DAF=∠BAE,AF=AE,
∴∠DAF+∠DAE=∠BAE+∠DAE=∠ABC=90°,
∴∠EAF=90°,
∴△AEF为等腰直角三角形;
(2)解:①∵AH⊥EF,
∴∠AGF=90°,
∵∠ADF=90°,
∴∠AGF=∠ADF,
∵∠GIA=∠DIF,
∴∠GAI=∠DFE=30°,
∴GI=AI cos30°=2,
由(1)知:△AEF是等腰直角三角形,
∴∠AEF=∠AFE=45°,
∴AF;
②由①知:∠GAI=∠DFE,
∴tan∠GAI=tan∠DFE,
∴,
由①知:∠AEF=45°,
∴tan∠AEF,
∴AG=EG,
∴,
∵四边形ABCD是正方形,
∴AD∥CB,
∴△AGI∽△HGE,
∴.
28.(2023秋 拱墅区期末)如图,四边形ABCD内接于⊙O,对角线AC平分∠BAD,连接BD交AC于点E.
(1)求证:△ABC∽△BEC.
(2)若AB=AC,设△ABD的面积为S1,△BCD的面积为S2,BE=6,EC=4,求的值.
(3)求证:AC2=BC2+AB AD.
【分析】(1)根据圆周角定理可得∠CBD=∠CAD,由角平分线定义得∠BAC=∠CAD,即可证得结论;
(2)过点A作AF⊥BD于点F,过点C作CG⊥BD于点G,可证得△CAB∽△CBE,可得,即,求得AE=5,再证得△AEF∽△CEG,即可求得答案;
(3)先证明△ACB∽△ADE,可得AC AE=AB AD,即AC2﹣AC CE=AB AD,再证得△CBE∽△CAB,可得AC CE=BC2,即可证得结论.
【解答】(1)证明:∵四边形ABCD是圆内接四边形,
∴∠CBD=∠CAD,
∵AC平分∠BAD,
∴∠BAC=∠CAD,
∴∠CBD=∠BAC,
∴△ABC∽△BEC.
(2)解:如图,过点A作AF⊥BD于点F,过点C作CG⊥BD于点G,
∵AB=AC,
∴∠ABC=∠ACB,
∵AC平分∠BAD,
∴∠BAC=∠CAD,
∴,
∴∠BAC=∠CBD,
∴△CAB∽△CBE,
∴∠BEC=∠ABC=∠ACB,,
又∵BE=6,EC=4,
∴BC=BE=6,
∴,
∴AE=5,
∵AF⊥BD,CG⊥BD,
∴∠AFE=∠CGE=90°,
∵∠AEF=∠CEG,
∴△AEF∽△CEG,
∴,
∴.
(3)证明:∵AC平分∠BAD,
∴∠BAC=∠CAD,
∵,
∴∠ACB=∠ADB,
∴△ACB∽△ADE,
∴,
∴AC AE=AB AD,
∴AC (AC﹣CE)=AB AD,
∴AC2﹣AC CE=AB AD,
∵,
∴∠CBD=∠BAC,
∵∠BCE=∠ACB,
∴△CBE∽△CAB,
∴,
∴AC CE=BC2,
∴AC2﹣BC2=AB AD,
即AC2=BC2+AB AD.
29.(2023秋 滨江区期末)如图,在⊙O中,弦AB是直径,点C,D是⊙O上的两点,连结AC,OD,且满足AC∥OD.
(1)若的度数为80°,求∠A的度数.
(2)求证:.
(3)连结BD,若AC=6,AB=10,求BD的长.
【分析】(1)连接OC,根据弧AC的度数求出∠AOC,利用三角形内角和求出∠A;
(2)利用平行线的性质求得∠BOD=∠A=50°,∠COD=∠OCA=50°,得出∠COD=∠BOD,进而得出弧相等;
(3)先根据勾股定理求出BC,然后利用勾股定理求出OE,再利用勾股定理求出BD即可.
【解答】(1)解:连接OC,
∵的度数为80°,
∴∠AOC=80°,
∵OA=OC,
∴∠A=∠OCA=50°;
(2)证明:∵AC∥OD,
∴∠BOD=∠A,∠COD=∠OCA,
∵OA=OC,
∴∠A=∠OCA,
∴∠COD=∠BOD,
∴;
(3)解:连接BC,交OD于点E,
∵弦AB是直径,
∴∠ACB=90°,
∵AC=6,AB=10,
∴BC8,
∵,
∴OD⊥BC,
∴CE=BE=4,
∴OE3,
∴DE=OD﹣OE=2,
∴BD2.
30.(2023秋 拱墅区校级期末)如图,已知正方形ABCD的边长为12,点E是射线BC上一点(点E不与点B、C重合),过点A作AF⊥AE,交边CD的延长线于点F,直线EF分别交射线AC、射线AD于点M、N.
(1)求证:△ABE≌△ADF;
(2)当点E在边BC上时,如果AN=5DN,求∠BAE的正切值.
(3)当点E在边BC延长线上时,设线段BE=x,y=EN MF,求y关于x的函数解析式.
【分析】(1)根据正方形的性质得AB=AD,∠B=∠ADC=90°=∠ADF,根据同角的与角相等得∠BAE=∠DAF,利用ASA即可得△ABE≌△ADF;
(2)根据全等三角形、相似三角形的性质以及锐角三角函数的定义进行计算即可;
(3)利用等腰三角形的性质,相似三角形的性质得出EN MF=AE2,再根据勾股定理得出AE2=36+x2即可.
【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=AD=12,∠B=∠ADC=90°=∠ADF,
∵AE⊥AF,
∴∠EAF=90°=∠DAF+∠DAE,
∵∠BAE+∠DAE=∠BAD=90°,
∴∠BAE=∠DAF,
∴△ABE≌△ADF(ASA);
(2)解:∵△ABE≌△ADF,
∴AE=AF,DF=BE,
∵AN=5DN,AD=12=DN+AN,
∴DN=2,AN=10,
∵DN∥EC,
∴,
设BE=x,则DF=x,EC=12﹣x,
∴,
解得x=4或x=6,
经检验,x=4,x=6都是原方程的根,
∴BE=4或BE=6,
在Rt△ABE中,
tan∠BAE或tan∠BAE,
∴∠BAE的正切值为或;
(3)如图,
由(1)得AE=AF,
∵AE⊥AF,
∴△AEF是等腰直角三角形,
∴∠AEF=∠AFE=45°,
∵∠AEF=45°=∠MAN,∠M=∠M,
∴△MAN∽△MFA,
∴∠ANE=∠MAF,
∴△ANE∽△MAF,
∴,
∴EN MF=AE AF=AE2,
在Rt△ABE中,AB=12,BE=x,
∴AE2=AB2+BE2=144+x2,
∴y=EN MF,
∴y=144+x2(x>12).
31.(2023秋 杭州期末)如图,⊙O是Rt△ABC的外接圆,点D是弧AB的中点,过点D作AB的平行线交CA的延长线于点E,连结BD,BE.
(1)求证:∠EDC=∠DBC;
(2)当CD=2时,求S△BCE的值;
(3)设BC=nAC.
①求的值;(用含n的代数式表示)
②若3CE=8AC,DE=6,求AB的长.
【分析】(1)连接AD,利用平行线的性质,同弧作对的圆周角相等,通过等量代换证明即可;
(2)通过证明△CDE∽△CBD,求出BC CE=4,即可求三角形的面积;
(3)①过D点作DG⊥AE交于G点,由题可得tan∠CAB=n,设GE=a,则GD=na,分别求出CDna,CE=a+na,BC,再由△CDE∽△CBD,得到,;
②由①可知BC,则AC,则AB,根据题意分别得到36=a2(1+n2),3(a+na)=8 ,求出n=3或n,再求AB的长即可.
【解答】(1)证明:连接AD,
∵ED∥AB,
∴∠ADE=∠BAD,
∵点D是弧AB的中点,
∴∠CDB=∠ECD,
∵∠ACB=90°,
∴∠BCD=45°,
∵,
∴∠BCD=∠BAD,
∵,
∴∠ACD=∠CBA,
∴∠EDC=∠CBD;
(2)解:∵∠ECD=∠BCD,∠EDC=∠CBD,
∴△CDE∽△CBD,
∴CD2=BC CE,
∵CD=2,
∴BC CE=4,
∴S△BCEBC CE=2;
(3)①解:过D点作DG⊥AE交于G点,
∵BC⊥AE,
∴DG∥BC,
∴∠CED=∠ACB,
∵BC=nAC,
∴tan∠CAB=n,
设GE=a,则GD=na,
∵∠ACB=45°,
∴CG=GD=na,
∴CDna,CE=a+na,
∵CD2=BC CE,
∴2n2a2=(a+na)BC,
解得BC,
∵△CDE∽△CBD,
∴,
∴;
②解:由①可知BC,则AC,
∴AB,
∵DE6,
∴36=a2(1+n2),
∵3CE=8AC,
∴3(a+na)=8 ,
解得n=3或n,
当n=3时,a,则AB=9;
当n时,a,则AB=3;
综上所述:AB=9或3.
32.(2023秋 杭州期末)如图1,在△ABC中,AB=AC,∠A=90°,点P是△ABC内一个动点,且∠BPC=135°.
(1)试找出与∠ACP相等的角,并说明理由;
(2)如图2,连接AP并延长交△BPC的外接圆⊙O于点Q,交BC于点D,连接CQ.
①求证△ACP∽△AQC;
②求的最小值;
(3)在如图2的条件下,若BP=PC,求证:.
【分析】(1)根据∠ACB=∠ACP+∠BCP=45°,∠PBC+∠PCB=45°,等量代换即可得到∠ACP=∠PBC;
(2)①根据同弧所对的圆周角相等,结合(1)能得到∠Q=∠APC,即可证明;
②连接OB、CO,由△ACP∽△AQC,得到,当CQ经过圆心O时,的值最小,过点O作OM⊥BC交于M点,则M是BC的中点,连接AM,则A、O、M三点共线,则AO是BC的垂直平分线,再由CO=AC,得到CQ=2AC,即可求的最小值为;
(3)由题意可知P点AM上,则∠PBC=∠PCB=∠ACP,过点P作PH⊥AC交于H点,设PM=x,则PH=x,分别求出APx,AM=(1)x,AC(1)x,PC2=(4+2)x2,再由,即可证明.
【解答】(1)解:∵∠BPC=135°,
∴∠PBC+∠PCB=45°,
∵AB=AC,∠A=90°,
∴∠ACB=∠ACP+∠BCP=45°,
∴∠ACP=∠PBC;
(2)①证明:∵,
∴∠Q=∠PBC,
∵∠ACP=∠PBC,
∴∠Q=∠APC,
∴△ACP∽△AQC;
②连接OB、CO,
∵∠BPC=135°,
∴∠BOC=90°,
∵△ACP∽△AQC,
∴,
∴,
当CQ经过圆心O时,的值最小,
过点O作OM⊥BC交于M点,则M是BC的中点,连接AM,则A、O、M三点共线,
∴AO是BC的垂直平分线,
∵AM=BM=OM,
∴CO=AC,
∴CQ=2AC,
∴的最小值为;
(3)证明:∵BP=PC,
∴P点AM上,
∴∠PBC=∠PCB=∠ACP,
过点P作PH⊥AC交于H点,
∴PH=PM,
设PM=x,则PH=x,
∵∠PAH=45°,
∴APx,
∴AM=(1)x,AC(1)x,PC2=(4+2)x2,
∵,
∴()2,
∴CQ2=(2)AC2.
33.(2022秋 滨江区期末)如图1,在⊙O中,AB为弦,CD为直径,且AB⊥CD于点E,过点B作BF⊥AD,交AD的延长线于点F.连接AC,BO.
(1)求证:∠CAE=∠ADC.
(2)若DE=2OE,求的值.
(3)如图2,若BO的延长线与AC的交点G恰好为AC的中点,若⊙O的半径为r.求图中阴影部分的面积(结果用含r的代数式表示).
【分析】(1)由圆周角定理可得∠CAD=∠CAE+∠DAE=90°,再根据AB⊥CD,易得∠ADC+∠DAE=90°,即可证明∠CAE=∠ADC;
(2)连接BD,设OE=a,则DE=2a,OB=OD=3a,由勾股定理可得,,再证明△BOE∽△BDF,由相似三角形的性质可得,代入数值可求得,即可获得答案;
(3)连接BD,首先证明△OBE≌△DAE,结合全等三角形的性质进一步证明△OBD为等边三角形,即有∠BOD=60°;利用勾股定理、等边三角形的性质以及含30度角的直角三角形的性质依次求得OE、BE、AB、BF、AF等的值,然后由S阴影=S△ABF﹣S△DAE﹣(S扇形OBD﹣S△OBE)即可获得答案.
【解答】解:(1)∵CD为⊙O直径,
∴∠CAD=90°,即∠CAE+∠DAE=90°,
又∵AB⊥CD,
∴∠ADC+∠DAE=90°,
∴∠CAE=∠ADC;
(2)如图,连接BD,
∵AB⊥CD,DE=2OE,
∴OD=DE+OE=3OE,
设OE=a,则DE=2a,OB=OD=3a,
∴在Rt△OBE中,,
∴在Rt△DBE中,,
∵CD为⊙O直径,且AB⊥CD,
∴BE=AE,
∴AD=BD,
∴∠DAB=∠DBA,
∴∠BDF=∠DAB+∠DBA=2∠DAB,
又∵,
∴∠DOB=2∠DAB=∠BDF,
∵∠OEB=∠DFB=90°,
∴△BOE∽△BDF,
∴,即,
解得,
∴;
(3)如图,连接BD,
∵BO的延长线与AC的交点G恰好为AC的中点,
∴OG⊥AC,即∠OGC=∠CAD=90°,
∴BG∥AD,
∴∠OBE=∠DAE,
又∵BE=AE,∠OEB=∠DEA,
∴△OBE≌△DAE(ASA),
∴OB=DA,
∵CD为⊙O直径,AB⊥CD,
∴,
∴DA=DB,
∴OD=OB=DB,即△OBD为等边三角形,∠BOD=60°,
∵⊙O的半径为r,
∴OB=r,,
∴,
∴,
∵,
∴,
∴,
∴,
∵△OBE≌△DAE,
∴S△OBE=S△DAE,
∴S阴影=S△ABF﹣S△DAE﹣(S扇形OBD﹣S△OBE)
=S△ABF﹣S扇形OBD
.
34.(2022秋 杭州期末)如图,⊙O的半径为1,直径AB,CD的夹角∠AOD=60°,点P是上一点,连接PA,PC分别交CD,AB于点M,N.
(1)若PC⊥AB,求证:PA⊥CD.
(2)当点P在上运动时,
①猜想:线段AM与CN有怎样的数量关系,并给出证明.
②求证:PA+PC.
【分析】(1)由圆周角定理得出∠BAP=30°,由三角形内角和定理可求出∠AMO=90°,则可得出结论;
(2)①连接AD,证出∠D=60°,OA=AD=OD,证明△ADM≌△CON(ASA),由全等三角形的性质得出AM=CN;
②证明△AOM∽△APN,由相似三角形的性质得出,证明△CON∽△CPM,由相似三角形的性质得出,由全等三角形的性质得出AM=CN,DM=ON,代入PA+PC并化简整理可得出答案.
【解答】(1)证明:∵∠AOD=∠BOC=60°,PC⊥AB,
∴60°,
∴∠BAP=30°,
∴∠AMO=180°﹣∠MAO﹣∠AOM=180°﹣30°﹣60°=90°,
∴PA⊥CD;
(2)解:①AM=CN.
证明:连接AD,
∵OA=OD,∠AOD=60°,
∴△OAD是等边三角形,
∴∠D=60°,OA=AD=OD,
∵OC=OD,∠BOC=∠AOD=60°,
∴AD=OC,∠D=∠BOC=60°,
又∵∠DAP=∠DCP,
∴△ADM≌△CON(ASA),
∴AM=CN;
②证明:∵⊙O的半径为1,
∴OA=OB=OC=OD=1,
∵∠P=∠D=60°,∠AOD=60°,
∴∠P=∠AOD,
又∵∠BAP=∠BAP,
∴△AOM∽△APN,
∴,
∴,即PA,
∵∠BOC=∠CPM=60°,∠C=∠C,
∴△CON∽△CPM,
∴,
∴PC,
∵△ADM≌△CON,
∴AM=CN,DM=ON,
又∵DM+OM=OD=1,
∴PA+PC.
35.(2022秋 杭州期末)如图,BD是矩形ABCD的对角线,,点E,F分别在边AD,BC上,把△ABE和△CDF分别沿直线BE,DF折叠,使点A,C分别落在对角线BD上的点G,H处,连接FG.
(1)求证:BH=DG.
(2)若AB=6,AD=8,求线段FG的长.
(3)若FG∥CD,求的值.
【分析】(1)根据矩形性质可得AB=CD,由折叠得:BG=AB,DH=CD,推出BG=DH,即可证得结论;
(2)利用勾股定理可得BD=10,设FH=CF=x,利用S△CDF+S△BDF=S△BCD,建立方程可求得x=3,再利用勾股定理即可求得答案;
(3)由相似三角形性质可得出,设k,AB=a,则BC=k AB=ka,AD=BC=ka,利用勾股定理可得BDa,再利用折叠性质可得DG,由BG+DG=BD,可得aa,解得:k2,即可求得答案.
【解答】(1)证明:∵四边形ABCD是矩形,
∴AB=CD,
由折叠得:BG=AB,DH=CD,
∴BG=DH,
∴BD﹣DH=BD﹣BG,
即BH=DG.
(2)解:∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB=CD,AD=BC,
∵AB=6,AD=8,
∴BD10,
∵BG=DH=AB=6,
∴GH=BG+DH﹣BD=6+6﹣10=2,
由折叠得:∠DHF=∠C=90°,FH=CF,设FH=CF=x,
∵S△CDF+S△BDF=S△BCD,
∴6x10x6×8,
解得:x=3,
∴FH=3,
在Rt△FGH中,FG,
∴线段FG的长为.
(3)解:∵FG∥CD,
∴△BFG∽△BCD,
∴,
∵AB=CD=BG,
∴,
设k,AB=a,则BC=k AB=ka,AD=BC=ka,
∵,
∴1<k,
∴BDa,
∵FG∥CD,
由折叠得∠FDG=∠FDC,BG=AB=a,
∴∠DFG=∠FDG,
∴DG=FG,
∵,
∴,
∴FG,
∴DG,
∵BG+DG=BD,
∴aa,
解得:k2,
∴,
故的值为.
36.(2022秋 上城区期末)如图,E是矩形ABCD边BC上的一点,作DF⊥DE交BA的延长线于点F,连结EF交AD于点G.
(1)求证:△DCE∽△DAF;
(2)已知DC=1,BC=3,
①若G为AD中点,求FG:GE的值;
②若△DGE为等腰三角形,求CE的长.
【分析】(1)根据矩形的性质、垂直的定义得到∠DAB=∠ADC=∠C=90°=∠DAF,结合邻补角定义推出∠ADF=∠CDE,即可判定△DCE∽△DAF;
(2)①根据相似三角形的性质得出AF=3CE,过点G作GM⊥BC于点M,根据矩形的判定与性质、平行线分线段成比例推出,,据此求解即可;
②分三种情况根据等腰三角形的性质求解即可.
【解答】(1)证明:∵四边形ABCD是矩形,
∴∠DAB=∠ADC=∠C=90°,
∵∠DAF+∠DAB=180°,
∴∠DAF=90°=∠C,
∵DF⊥DE,∠ADC=90°,
∴∠ADF+∠GDE=∠GDE+∠CDE=90°,
∴∠ADF=∠CDE,
∴△DCE∽△DAF;
(2)解:①∵△DCE∽△DAF,
∴,
∵DC=1,BC=AD=3,
∴,
∴AF=3CE,
过点G作GM⊥BC于点M,
∵四边形ABCD是矩形,GM⊥BC,
∴四边形GMCD是矩形,
∴DG=CM,GM=CD=1,
∵G为AD中点,AD=BC,
∴CM=BMBC,
∵∠EMG=∠B=90°,
∴GM∥BF,
∴,
∴,
∴CE或1,
∴EM=1或,
∴或3,,
∴FG:GE的值为或3;
②分以下三种情况:
若DG=GE时,△DGE为等腰三角形,则DG=GE=FG,如图,过点G作GM⊥BC于点M,
∵,
∴1,
∴BM=EM,
∴,
∴,
∴CE;
若DE=GE时,△DGE为等腰三角形,如图,过点G作GM⊥BC于点M,
∵DE=GE,GM=CD,
∴Rt△CDE≌Rt△MGE,
∴EM=CE,
∴BE=3﹣CE,AG=BM=3﹣2CE,
∵AD∥BC,
∴△AFG∽△BFE,
∴,
∴,
∴CE或(舍去);
若DG=DE时,△DGE为等腰三角形,如图,连接BG,
∵DG=DE,
∴∠DGE=∠DEG,
∴AD∥BC,
∴∠DGE=∠GEB=∠DEG,
又∠FDE=∠FBE=90°,EF=EF,
∴△FDE≌△FBE(AAS),
∴DE=BE,
∴DG=DE=BE,
又∵DG∥BE,
∴四边形DGBE是菱形,
∴AG=CE,DG=3﹣CE,
在Rt△CDE中,DE2=CD2+CE2,
∴(3﹣CE)2=12+CE2,
∴CE;
综上,若△DGE为等腰三角形,CE的长为或或.
37.(2022秋 西湖区期末)如图,△ABC内接于⊙O,∠ABC>90°,△ABC的外角∠EAC的平分线交⊙O于点D,连接DB,DC,DB交AC于点F.
(1)求证:△DBC是等腰三角形.
(2)若DA=DF.
①求证:BC2=DC BF.
②若⊙O的半径为5,BC=6,求的值.
【分析】(1)由题意易得∠BCD+∠BAD=180°,则有∠EAD=∠BCD,进而可得∠EAD=∠DAC,则∠BCD=∠CBD,然后问题可求证;
(2)①由题意易证△DAF∽△DBC,则有∠ADF=∠BDC,进而可得∠DFA=∠DCB,再由相似三角形的判定得出△FBC∽△BCD,利用其性质即可证明;
②连接DO交BC于G,由题意易得D、O都在中垂线上,即D、O、G共线,进而可得DO⊥BC且BG=GC=3,则有DG=4+OD=9,由①得,根据相似三角形的性质得出,再由相似三角形的判定得出△AFD∽△BFC,利用其性质即可求解.
【解答】(1)证明:∵四边形ABCD内接于⊙O,
∴∠BCD+∠BAD=180°,
∵∠DAB+∠EAD=180°,
∴∠EAD=∠BCD,
∴∠CAD=∠CBD,
∵AD平分∠EAC,
∴∠EAD=∠DAC,
∴∠BCD=∠CBD,
∴DB=DC,
∴△DBC是等腰三角形;
(2)①证明:∵DA=DF,
∴∠DAF=∠DFA,
∴∠DAF=∠DFA=∠CBD=∠BCD,
∴△DAF∽△DBC,
∴∠ADF=∠BDC,
∴∠DFA=∠DCB,
∵∠DBC=∠FBC,
∴△FBC∽△BCD,
∴,
∴BC2=BD BF,
∵DB=DC,
∴BC2=DC BF;
②解:连接DO交BC于G,
∵BD=DC,OB=OC,
∴D、O都在中垂线上,即D、O、G共线,
∴DO⊥BC且BG=GC=3,
∵OB=5,
∴在Rt△BOG中,OG=4,
∴DG=4+OD=9,
∴在Rt△BDG中,,
∵△FBC∽△BCD,
∴,
∴,
解得:,
∴,
∴,
∵∠DAC=∠DBC,∠DFA=∠BFC,
∴△AFD∽△BFC,
∴,
∴.
38.(2022秋 西湖区校级期末)如图,AB、AC、AD是⊙O中的三条弦,点E在AD上,且AB=AC=AE.连结BC,BD,CD,其中BC交AD于点G.
(1)求证:△ABG∽△ADB.
(2)若∠DBE=α,求∠CAD的度数(用含α的代数式表示).
(3)若AD=15,AB=12,BD=6,求线段CD的长.
【分析】(1)由等弦所对弧相等,再由等弧所对圆周角相等得出∠ABC=∠ADB,又∠BAG=∠DAB,即可得出结论;
(2)由等边对等角的性质与圆周角性质得出∠DBE=∠CBE=α,即可由∠CAD=∠CBD=∠DBE+∠CBE求解;
(3)由△ABG∽△ADB,得,从而可求出,,从而求出,再证△BDG∽△ADC,得,代入即可求解.
【解答】(1)证明:∵AB=AC,
∴,
∴∠ABC=∠ADB,
又∵∠BAG=∠DAB,
∴△ABG∽△ADB;
(2)解:∵AB=AE,
∴∠AEB=∠ABE,
∴∠DBE+∠ADB=∠ABC+∠CBE,
∵AB=AC,,
∴∠ABC=∠ACB=∠ADB,
∴∠DBE=∠CBE=α,
∵,
∴∠CAD=∠CBD=∠DBE+∠CBE=2α;
(3)解:∵△ABG∽△ADB,
∴,
∵AD=15,AB=12,BD=6,
∴,
∴,,
∴,
∵∠CAD=∠CBD=2α,∠ADC=∠GDB,
∴△BDG∽△ADC,
∴,即,
∴.
39.(2022秋 西湖区校级期末)已知二次函数y=ax2﹣2(a+1)x+4(a≠0).
(1)证明:二次函数的图象与x轴总有交点.
(2)若点P(,b)和点Q(n,b)在该二次函数图象上,求(b)2+n2的值.
(3)将该二次函数图象向下平移2个单位,令新函数图象与x轴的交点横坐标为x1,x2.证明:|x1﹣x2|>2.
【分析】(1)计算出△,可以证明△大于等于0,即可说明图象与x轴总有交点;
(2)先求出抛物线对称轴,在根据P,Q关于对称轴对称求出n=2,再把点P坐标代入抛物线求出b=2,再求出(b)2+n2的值;
(3)求出平移后的新函数解析式,再由二次函数与方程的关系证明即可.
【解答】(1)证明:∵Δ=[﹣2(a+1)]2﹣4a×4=4a2+8a+4﹣16a=4a2﹣8a+4=4(a﹣1)2≥0,
∴二次函数的图象与x轴总有交点;
(2)解:∵y=ax2﹣2(a+1)x+4(a≠0),
∴抛物线对称轴为直线x1,
∵点P(,b)和点Q(n,b)关于对称轴对称,
∴1,
∴n=2,
把P(,b)代入函数解析式得:a2(a+1)4=b,
解得b=2,
∴(b)2+n2=(2)2+22=8;
(3)证明:∵将二次函数y=ax2﹣2(a+1)x+4(a≠0)的图象向下平移2个单位,
平移后的解析式为y=ax2﹣2(a+1)x+2,
∵平移后函数图象与x轴的交点横坐标为x1,x2,
∴ax2﹣2(a+1)x+2=0的两个根为x1,x2,
∴x1+x2,x1 x2,
∴|x1﹣x2|2.
40.(2022秋 西湖区期末)在直角坐标系中,设函数y=m(x+1)2+4n(m≠0,且m,n为实数),
(1)求函数图象的对称轴.
(2)若m,n异号,求证:函数y的图象与x轴有两个不同的交点.
(3)已知当x=0,3,4时,对应的函数值分别为p,q,r,若2q<p+r,求证:m<0.
【分析】(1)根据对称轴的定义解答即可;
(2)令y=0,则有,由m,n异号,可知一元二次方程有两个实数根,即函数y的图象与x轴有两个不同的交点;
(3)把x=0,3,4代入y=m(x+1)2+4n表示出p,q,r,再利用2q﹣(p+r)<0,解题即可.
【解答】(1)解:∵函数y=m(x+1)2+4n(m≠0,且m,n为实数),
∴函数图象的对称轴为x=﹣1;
(2)证明:令y=0,则0=m(x+1)2+4n,
即,
∵m,n异号,
∴,
∴一元二次方程有两个不相等的实数根,即函数y的图象与x轴有两个不同的交点;
(3)证明:由题可知p=m+4n,q=16m+4n,r=25m+4n,
∵2q﹣(p+r)=2(16m+4n)﹣(m+4n+25m+4n)=6m<0,
∴m<0.
41.(2022秋 上城区期末)二次函数y1=2(x﹣x1)(x﹣x2)(x1,x2是常数)的图象与x轴交于A,B两点.
(1)若A,B两点的坐标分别为(1,0),(2,0),求函数y1的表达式及其图象的对称轴;
(2)若函数y1的图象经过点(2,m),且x1+x2=2时,求m的最大值;
(3)若一次函数y2=kx+b(k,b是常数,k≠0),它的图象与y1的图象都经过x轴上同一点,且x1﹣x2=2.当函数y=y1+y2的图象与x轴仅有一个交点时,求k的值.
【分析】(1)利用待定系数法解答即可;
(2)将已知条件代入解析式中,得到m关于x1的函数关系式,利用二次函数的性质,配方法解答即可得出结论;
(3)利用分类讨论的思想方法分别得到y关于x1,x2的解析式,再利用待定系数法和已知条件解答即可.
【解答】解:二次函数y1=2(x﹣x1)(x﹣x2)=2x2﹣2(x1+x2)x+2x1x2,
∵二次函数y1=2(x﹣x1)(x﹣x2)经过(1,0),(2,0),
∴,
解得:,
∴函数y1的表达式为y1=2x2﹣6x+4.
∵y1=2x2﹣6x+4=2,
∴函数y1的对称轴为直线x;
(2)∵函数y1的图象经过点(2,m),
∴m=2×22﹣4(x1+x2)+2x1x2=8﹣4(x1+x2)+2x1x2,
∵x1+x2=2,
∴x2=2﹣x1,
∴m=8﹣4×2+2x1 (2﹣x1)
=﹣24x1
=﹣22,
∵﹣2<0,
∴当x1=1时,m有最大值为2.
∴m的最大值为2;
(3)由题意:二次函数y1=2(x﹣x1)(x﹣x2)(x1,x2是常数)的图象与x轴交于(x1,0),(x2,0)两点,
①若两函数的图象都经过x轴上同一点(x1,0),
∴0=kx1+b,
∴b=﹣kx1,
∴y2=kx﹣kx1.
∵y=y1+y2,
∴y=2x2﹣2(x1+x2)x+2x1x2+kx﹣kx1
=2x2﹣(2x1+2x2﹣k)x+2x1x2﹣kx1.
∵函数y=y1+y2的图象与x轴仅有一个交点,
∴Δ=0.
即0,
整理得:0,
∴k=﹣2(x1﹣x2).
∵x1﹣x2=2,
∴k=﹣2×2=﹣4;
②若两函数的图象都经过x轴上同一点(x2,0),
∴0=kx2+b,
∴b=﹣kx2,
∴y2=kx﹣kx2.
∵y=y1+y2,
∴y=2x2﹣2(x1+x2)x+2x1x2+kx﹣kx2
=2x2﹣(2x1+2x2﹣k)x+2x1x2﹣kx2.
∵函数y=y1+y2的图象与x轴仅有一个交点,
∴Δ=0.
即4×2(2x1x2﹣kx2)=0,
整理得:0,
∴k=2(x1﹣x2).
∵x1﹣x2=2,
∴k=2×2=4.
综上,当函数y=y1+y2的图象与x轴仅有一个交点时,k的值为4或﹣4.
42.(2022秋 杭州期末)在平面直角坐标系中,点(1,m),(2,n)在函数y=x2+bx+c(b,c是常数)的图象上.
(1)若m=2,n=3,求该函数的表达式.
(2)若n=3m,求证:该函数的图象经过点.
(3)已知点(3,0),(﹣1,y1),(4,y2)在该函数图象上,若m>0,n<0,试比较y1,y2的大小,并说明理由.
【分析】(1)把(1,2),(2,3)分别代入y=x2+bx+c中得到关于b、c的方程组,然后解方程组即可;
(2)把(1,m),(2,3m)分别代入y=x2+bx+c中得到关于b、c的方程组,解方程组得到抛物线解析式为y=x2+(2m﹣3)x+2﹣m,然后计算x时,y,从而可判断抛物线经过点(,);
(3)如图,由于x=1时,y>0;x=2时,y<0,抛物线经过点(3,0),则可判断抛物线的对称轴在直线x=2的右侧,在直线x=3的左侧,然后利用点(﹣1,y1)到对称轴的距离大于点(4,y2)到对称轴的距离,从而得到y1>y2.
【解答】(1)解:把(1,2),(2,3)分别代入y=x2+bx+c得,
解得,
∴抛物线解析式为y=x2﹣2x+3;
(2)证明:把(1,2),(2,3)分别代入y=x2+bx+c得,
解得,
∴抛物线解析式为y=x2+(2m﹣3)x+2﹣m,
∵当x时,y(2m﹣3)+2﹣m,
∴抛物线经过点(,);
(3)y1>y2.
理由如下:
如图,
∵m>0,n<0,
∴x=1时,y>0;x=2时,y<0,
∵抛物线经过点(3,0),
∴抛物线的对称轴在直线x=2的右侧,在直线x=3的左侧,
∴点(﹣1,y1)到对称轴的距离大于点(4,y2)到对称轴的距离,
而抛物线开口向上,
∴y1>y2.
43.(2022秋 杭州期末)已知二次函数y=ax2+bx+c(a>0)的图象经过点A(﹣1,1)和B(2,4).
(1)求a,b满足的关系式.
(2)当自变量x的值满足﹣1≤x≤2时,y随x的增大而增大,求a的取值范围.
(3)若函数图象与x轴无交点,求a2+b2的取值范围.
【分析】(1)把点A(﹣1,1)和B(2,4)代入解析式得到,两式相减即可得到结论;
(2)由题意可知1,代入b=1﹣a,解得a,即可得到a的取值范围是0<a;
(3)由b=1﹣a得到a2+b2=2(a)2,即可根据二次函数的性质得到a2+b2的最值.
【解答】解:(1)∵二次函数y=ax2+bx+c(a>0)的图象经过点A(﹣1,1)和B(2,4),
∴,
②﹣①得,3a+3b=3,即a+b=1,
∴b=1﹣a;
(2)由题意可知1,
∵b=1﹣a,
∴1,
∴a>0,
∴1﹣a≥2a,
∴a,
∴a的取值范围是0<a;
(3)∵函数图象与x轴无交点,
∴b2﹣4ac<0,即(1﹣a)2﹣4a(2﹣2a)<0,
∴(1﹣a)(1﹣9a)<0,
解得a<1,
∵b=1﹣a,
∴a2+b2
=a2+(1﹣a)2
=a2+a2﹣2a+1
=2a2﹣2a+1
=2(a)2,
∴当a时,a2+b2的最小值为,
当a=1时,a2+b2的最大值为1,
∴a2+b2<1.
44.(2022秋 滨江区期末)二次函数y=x2﹣bx+c的图象经过(﹣2,y1),(1,y2)两点.
(1)当b=1时,判断y1与y2的大小.
(2)当y1<y2时,求b的取值范围.
(3)若此函数图象还经过点(m,y1),且1<b<2,求证:3<m<4.
【分析】(1)当b=1时,分别把x=﹣2,x=1代入解析式,计算出y1,y2,比较即可;
(2)先求出y1=4+2b+c,y2=1﹣b+c,再根据y1<y2,解不等式即可;
(3)先求出二次函数y=x2﹣bx+c的对称轴为直线x,m得由1<b<2,计算可得答案.
【解答】解:(1)当b=1时,
∴,
∵6+c>c,
∴y1>y2;
(2)∵y1=4+2b+c,y2=1﹣b+c,
又∵y1<y2,
∴4+2b+c<1﹣b+c,
∴b<﹣1;
(3)二次函数y=x2﹣bx+c的对称轴为直线,
∵二次函数经过(﹣2,y1),(m,y1)两点,
∴m得,即m=2+b,
∵1<b<2,
∴3<m<4.
45.(2023秋 杭州期末)综合与实践:问题情境:求方程x2+x﹣1=0的解,就是求二次函数y=x2+x﹣1的图象与x轴交点的横坐标.为了估计这个方程的解,圆圆先取了6个自变量满足x1<x2<x3<x4<x5<x6且x1﹣x2=x2﹣x3=x3﹣x4=x4﹣x5=x5﹣x6,再分别算出相应的y值.列表得:
x的值 x1 x2 x3 x4 x5 x6
y=x2+x﹣1的值 1 0.71 0.44 0.19 0.04 ﹣0.25
操作判断:(1)求x1的值;
实践探究:(2)为了分析函数值的变化规律,圆圆将表格中得到的函数值逐个作差.如:0.71﹣1=﹣0.29,0.44﹣0.71=﹣0.27,得到如下数据:﹣0.29,﹣0.27,﹣0.25,﹣0.15,﹣0.29,通过计算,圆圆发现自己由于粗心算错了其中的一个函数值,请指出算错的是哪一个值,正确的是多少?
问题解决:(3)对于一般的二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的函数值变化进行如表研究:(d≠0)
x的值 x x+d x+2d x+3d x+4d x+5d
y=ax2+bx+c的值 y1 y2 y3 y4 y5 y6
将表格中得到的函数值逐个作差,发现函数值的差与自变量满足某种函数关系,请写出你的发现过程以及发现结论.
【分析】(1)把y=1代入y=x2+x﹣1,求得相应的x的值,根据函数值的变化选取合适的x的值;
(2)作差后的前三个数据分别是前一个数据的基础上增加0.02,第四个不是,所以猜测第五个函数值错了,设出第五个函数值为m,根据第五个函数值减去第四个函数值的值为﹣0.25+0.02列式计算即可;
(3)可设函数值的差为w,若自变量为x,那么和它相邻的自变量为x+d,分别求得它们的函数值,相减即可得到w.
【解答】解:(1)把y=1代入y=x2+x﹣1,得:
x2+x﹣1=1,
解得x1=﹣2,x2=1.
∵二次函数y=x2+x﹣1的对称轴为直线x,
∴当x时,y随着x的增大而减小.观察图表可得y随x的增大而减小.
∴.
∴x1=﹣2.
(2)作差后的前三个数据﹣0.29,﹣0.27,﹣0.25分别是前一个数的基础上增加0.02,第四个不是.
∴猜测第五个函数值错了.
设第5个函数值为m.
∴m﹣0.19=﹣0.25+0.02.
解得:m=﹣0.04.
答:第五个函数值错了,应该是﹣0.04.
(3)设函数值的差为w,
猜测:函数值的差与自变量满足一次函数关系,
若自变量为x,则函数值为:yn=ax2+bx+c;
和x相邻的自变量为x+d,则函数值为:yn+1=a(x+d)2+b(x+d)+c.
∴w=[a(x+d)2+b(x+d)+c]﹣(ax2+bx+c)
=2adx+(ad2+bd).
∵a,b,c,d为常数,且a≠0,d≠0,
∴函数值的差与自变量满足一次函数关系.w=2adx+(ad2+bd)(a≠0,d≠0,a、b、c、d为常数).
46.(2023秋 杭州期末)已知二次函数y=ax2﹣2ax+1(a≠0),图象经过点(﹣1,m),(1,n),(3,p).
(1)当m=﹣2时.
①求二次函数的表达式;
②写出一个符合条件的x的取值范围,使得y随x的增大而增大;
(2)若在m,n,p这三个实数中,只有一个是正数,求证:.
【分析】(1)①利用待定系数法即可解决问题.
②根据所得二次函数的图象和性质即可解决问题.
(2)由这三个点在抛物线上的位置即可解决问题.
【解答】解:(1)①当m=﹣2时,
将点(﹣1,﹣2)代入函数解析式得,
a+2a+1=﹣2,
解得a=﹣1.
所以二次函数的表达式为y=﹣x2+2x+1.
②因为抛物线的对称轴为直线x,且开口向下,
所以当x<1时,y随x的增大而增大.
故一个符合条件的x的取值范围是:x<1.
证明:(2)因为抛物线的对称轴为直线x,
又因为1﹣(﹣1)=3﹣1,
所以点(﹣1,m)和点(3,p)关于抛物线的对称轴对称,
则m=p.
又因为m,n,p这三个实数中,只有一个是正数,
所以m和p都是非正数,n是正数,
则,
解得.
所以a.
47.(2023秋 拱墅区校级期末)已知二次函数y=x2﹣4x﹣5,点P1(x1,y1)与P2(x2,y2)都在该函数的图象上,且x1+x2=2.
(1)求函数图象的顶点;
(2)若点P1(x1,y1)与P2(x2,y2)与直线x=m的距离恒相等,求m的值;
(3)若y1≥y2,求y1的最小值.
【分析】(1)把解析式化成顶点式即可求解;
(2)根据题意,列出方程,化简后将x1+x2=2代入即可求解;
(3)根据题意,由(1)(2)可得,P1在直线x=1的左侧,P2在直线x=1的右侧或重合在直线x=1上,根据二次函数的增减性即可求解.
【解答】解(1)∵二次函数y=x2﹣4x﹣5=(x﹣2)2﹣9,
∴函数图象的顶点为(2,﹣9).
(2)∵点P1(x1,y1)与P2(x2,y2)与直线x=m的距离恒相等,
∴|x1﹣m|=|x2﹣m|,
∴(x1﹣m)2=(x2﹣m)2,
化简得(x1﹣x2)[(x1+x2)﹣2m]=0,
又∵x1+x2=2,x1≠x2,
∴m=1.
故m的值为1.
(3)∵y1≥y2,
由(1)(2)可得,P1在直线x=1的左侧,P2在直线x=1的右侧或重合在直线x=1上,
∴x1≤1,
∵y1随x1的增大而减小,
∴当x1=1时,y1的最小值为﹣8.
故y1≥y2时,y1的最小值为﹣8.
48.(2023秋 滨江区期末)【综合与实践】
【认识研究对象】教材121页给出了如下定义:如图1,如果点P把线段AB分成两条线段AP和PB(AP>PB),且,则我们称点P为线段AB的黄金分割点.类似,我们可以定义:如果一个三角形中,其最长边的长度和最短边的长度的乘积等于第三边长度的平方,那么就称该三角形为“类黄金三角形”.
如图2,已知△ABC是“类黄金三角形”,且AC<AB<BC.若AC=3,BC=5,求AB的长.
【探索研究方法】如图3,已知△ABC是“类黄金三角形”,且AC<AB<BC.
若∠BAC=90°,小滨同学过点A作AD⊥BC于点D,发现了两个结论:
①AB2=BD×BC;
②点D是边BC的黄金分割点;
请给出证明.
【尝试问题解决】小滨同学经历以上探索过程发现:类似问题,可以通过构造相似三角形等方法解决.于是开展新的探
浙江省杭州市近2年各区期末考试压轴题集中训练卷
一.选择题(共13小题)
1.(2023秋 上城区期末)已知二次函数y=a(x+m﹣1)(x﹣m)(a≠0)的图象上有两点A(x1,y1)和B(x2,y2)(其中x1<x2),则( )
A.若a>0,当x1+x2<1时,a(y1﹣y2)<0
B.若a>0,当x1+x2<1时,a(y1﹣y2)>0
C.若a<0,当x1+x2>﹣1时,a(y1﹣y2)<0
D.若a<0,当x1+x2>﹣1时,a(y1﹣y2)>0
2.(2023秋 西湖区期末)已知二次函数y=a(x﹣h)2+k(a≠0)的图象与一次函数y=px+q(p≠0)的图象交于(x1,y1)和(x2,y2)两点,则下列结论正确的是( )
A.若a>0,p<0,则x1+x2>2h
B.若x1+x2>2h,则a>0,p<0
C.若a<0,p<0,则x1+x2>2h
D.若x1+x2>2h,则a<0,p<0
3.(2023秋 拱墅区期末)如图,四边形ABCD内接于⊙O,其中AD>CD,已知对角线AC过点O,对角线BD与CO相交于点E,且AD=BD.若∠BDC=2∠DBC,则( )
A.1 B. C.2 D.3
4.(2023秋 滨江区期末)在平面直角坐标系中,已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0),当y≥t时,x≤m﹣1或x≥m+3.若该函数图象过点A(m,5)和B(m+4,q),则q的值可能是( )
A.3 B.4 C.5 D.6
5.(2023秋 拱墅区校级期末)如图,AB是⊙O的直径,点C,D在⊙O上,且∠OAC=30°,OD绕着点O顺时针旋转,连接CD交直线AB于点E,当DE=OD时,∠OCE的大小不可能为( )
A.20° B.40° C.70° D.80°
6.(2023秋 杭州期末)如图,正△ABC纸片,E为AC边上的一点,连结BE.将△BAE沿BE翻折得到△BFE,过点C作AB的平行线交EF的延长线于点M,若∠EMC=90° 则的比为( )
A. B. C. D.
7.(2023秋 杭州期末)如图,△ABC内接于⊙O,∠ABC>90°,它的外角∠EAC的平分线交⊙O于点D,连接DB,DC,DB交AC于点F.若DA=DF,∠ABC=α,∠DFC=β,则下列结论正确的是( )
A.α+4β=540° B.α+4β=450° C.α+2β=360° D.α+2β=270°
8.(2022秋 滨江区期末)二次函数y=ax2+4x+1(a为实数,且a<0),对于满足0≤x≤m的任意一个x的值,都有﹣2≤y≤2,则m的最大值为( )
A. B. C.2 D.
9.(2022秋 杭州期末)计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图:
当任务完成的百分比为x时,线段MN的长度记为d(x).下列描述正确的是( )
A.当x1>x2时,d(x1)>d(x2)
B.当d(x1)>d(x2)时,x1>x2
C.当x1+x2=1时,d(x1)=d(x2)
D.当x1=2x2时,d(x1)=2d(x2)
10.(2022秋 杭州期末)已知点P(m,n),Q(3,0)都在一次函数y=kx+b(k,b是常数,k≠0)的图象上,( )
A.若mn有最大值4,则k的值为﹣9
B.若mn有最小值4,则k的值为﹣9
C.若mn有最大值﹣9,则k的值为4
D.若mn有最小值﹣9,则k的值为4
11.(2022秋 上城区期末)如图,AD是△ABC的外角平分线,与△ABC的外接圆交于点D,连结BD交AC于点F,且BC=CF,则下列结论错误的是( )
A.∠ADB=∠CDB B.3∠ACB+∠ACD=180°
C.3∠BDC+2∠ABD=180° D.3∠BAD+∠ABD=360°
12.(2022秋 西湖区期末)设函数y1=﹣(x﹣a1)2,y2=﹣(x﹣a2)2.直线x=1的图象与函数y1,y2的图象分别交于点A(1,c1),B(1,c2),得( )
A.若1<a1<a2,则c1<c2 B.若a1<1<a2,则c1<c2
C.若a1<a2<1,则c1<c2 D.若a1<a2<1,则c2<c1
13.(2022秋 西湖区校级期末)如图,将矩形ABCD沿着GE,EC,GF翻折,使得点A,B,D恰好都落在点O处,且点G,O,C在同一条直线上,点E,O,F在另一条直线上.以下结论正确的是( )
A.△COF∽△CEG B.OC=3OF C.AB:AD=4:3 D.GEDF
二.填空题(共12小题)
14.(2023秋 上城区期末)如图,学校要在校园内建一个矩形的开心农场,其中一边AD是围墙,且AD的长不能超过28m,其余三边AB,BC,CD用60m长的铁质栅栏.有下列结论:
①AB的长可以为15m;
②当农场ABCD面积为200m2时,满足条件的AB的长只有一个值;
③农场ABCD面积的最大值为450m2;
④若把农场的形状改成半圆形,且直径一侧利用已有围墙,则农场的面积可以超过560m2.
其中,正确结论的是 .(只需填序号)
15.(2023秋 西湖区期末)如图,已知AB是⊙O的直径,弦CD⊥AB于点E,OE=BE.点P是劣弧上任意一点(不与点A,D重合),CP交AB于点M,AP与CD的延长线相交于点F,设∠PCD=α.
①则∠F= ,(用含α的代数式表示);
②当∠F=3∠PCD时,则 .
16.(2023秋 拱墅区期末)已知点(3,m),(5,n)在抛物线y=ax2+bx(a,b为实数,a<0)上,设抛物线的对称轴为直线x=t,若n<0<m,则t的取值范围为 .
17.(2023秋 滨江区期末)在平面直角坐标系中,二次函数y=ax2+2x+c(a,c是常数,且a≠0)的图象与x轴的一个交点坐标为(﹣2n,0).若该函数图象的顶点坐标为(n,p),则 .
18.(2023秋 拱墅区校级期末)如图,在Rt△ABC中,∠ACB=90°,把Rt△ABC沿斜边AB折叠,得到△ABD,过点D作DE⊥CA交CA的延长线于点E,过点C作CN∥AD,分别交AB,BD于点M,N,若CM=3,,则 .
19.(2023秋 杭州期末)数学家菲尔贝提出借助图形代替演算的观点,这类图形称为“诺模图”.如图是关于x,y,z三者关系的诺模图,它是由点O出发的三条射线a,b,c组成,每条射线上都有相同的刻度,且射线端点刻度为0,其中a和c,b和c都相交成60°角.在射线a和b上分别取点A和B,对应的刻度值是x和y.用直尺连结AB交射线c于点C,点C的刻度值就是z的值.
(1)若x=20,y=12,则z的值是 ;
(2)若x=2y,则 .
20.(2023秋 杭州期末)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,D、E为AB边上两点(点D在点E的右侧),满足∠DCE=45°,则AB边上的高为 ;设AD=x,BE=y.用含x的代数式表示y= .
21.(2022秋 滨江区期末)如图,正五边形ABCDE的对角线AC和AD分别交对角线BE于点M,N,若△AMN的面积为s,则正五边形ABCDE的面积为 (结果用含s的代数式表示).
22.(2022秋 杭州期末)如图,在正方形ABCD中,点E在边BC上(不与点B,C重合),点F在边CD的延长线上,DF=BE,连接EF交AD于点G,过点A作AN⊥EF于点M,交边CD于点N.若DN=2CN,BE=3.则CN= ,AM= .
23.(2022秋 上城区期末)如图,在矩形ABCD中,AD=4AB.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G,则 .
24.(2022秋 西湖区期末)如图,线段AB是⊙O的直径,弦CD⊥AB于点H,点M是弧BC上任意一点(不与B,C重合),AH=1,CH=2.延长线段BM交DC的延长线于点E,直线MH交⊙O于点N,连结BN交CE于点F,则OC= ,HE HF= .
25.(2022秋 西湖区校级期末)已知关于x的一元二次方程(x﹣2)(x﹣3)=m有实根x1,x2,且x1<x2,现有下列说法:①当m=0时,x1=2,x2=3;②当m>0时,2<x1<x2<3;③m;④二次函数y=(x﹣x1)(x﹣x2)﹣m的图象与x轴的交点坐标为(2,0)和(3,0).其中正确的有 .
三.解答题(共26小题)
26.(2023秋 上城区期末)如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.
(1)求证:△DOE∽△ABC;
(2)求证:∠ODF=∠BDE;
(3)连接OC,设△DOE的面积为S1,四边形OCBD的面积为S2,若,用含n的代数式表示.
27.(2023秋 西湖区期末)如图,E是正方形ABCD边BC上一个动点(不与B,C重合),F是CD延长线上一点,且DF=BE,连接AE,AF,EF.
(1)求证:△AEF为等腰直角三角形.
(2)过点A作EF的垂线,与直线EF,BC分别交于G,H两点,记∠DFE=α,EF交AD于点I.
①当α=30°,AI=2,求线段AE的长.
②设,△AGI的面积记作S1,△HGE的面积记作S2,用含k的代数式表示.
28.(2023秋 拱墅区期末)如图,四边形ABCD内接于⊙O,对角线AC平分∠BAD,连接BD交AC于点E.
(1)求证:△ABC∽△BEC.
(2)若AB=AC,设△ABD的面积为S1,△BCD的面积为S2,BE=6,EC=4,求的值.
(3)求证:AC2=BC2+AB AD.
29.(2023秋 滨江区期末)如图,在⊙O中,弦AB是直径,点C,D是⊙O上的两点,连结AC,OD,且满足AC∥OD.
(1)若的度数为80°,求∠A的度数.
(2)求证:.
(3)连结BD,若AC=6,AB=10,求BD的长.
30.(2023秋 拱墅区校级期末)如图,已知正方形ABCD的边长为12,点E是射线BC上一点(点E不与点B、C重合),过点A作AF⊥AE,交边CD的延长线于点F,直线EF分别交射线AC、射线AD于点M、N.
(1)求证:△ABE≌△ADF;
(2)当点E在边BC上时,如果AN=5DN,求∠BAE的正切值.
(3)当点E在边BC延长线上时,设线段BE=x,y=EN MF,求y关于x的函数解析式.
31.(2023秋 杭州期末)如图,⊙O是Rt△ABC的外接圆,点D是弧AB的中点,过点D作AB的平行线交CA的延长线于点E,连结BD,BE.
(1)求证:∠EDC=∠DBC;
(2)当CD=2时,求S△BCE的值;
(3)设BC=nAC.
①求的值;(用含n的代数式表示)
②若3CE=8AC,DE=6,求AB的长.
32.(2023秋 杭州期末)如图1,在△ABC中,AB=AC,∠A=90°,点P是△ABC内一个动点,且∠BPC=135°.
(1)试找出与∠ACP相等的角,并说明理由;
(2)如图2,连接AP并延长交△BPC的外接圆⊙O于点Q,交BC于点D,连接CQ.
①求证△ACP∽△AQC;
②求的最小值;
(3)在如图2的条件下,若BP=PC,求证:.
33.(2022秋 滨江区期末)如图1,在⊙O中,AB为弦,CD为直径,且AB⊥CD于点E,过点B作BF⊥AD,交AD的延长线于点F.连接AC,BO.
(1)求证:∠CAE=∠ADC.
(2)若DE=2OE,求的值.
(3)如图2,若BO的延长线与AC的交点G恰好为AC的中点,若⊙O的半径为r.求图中阴影部分的面积(结果用含r的代数式表示).
34.(2022秋 杭州期末)如图,⊙O的半径为1,直径AB,CD的夹角∠AOD=60°,点P是上一点,连接PA,PC分别交CD,AB于点M,N.
(1)若PC⊥AB,求证:PA⊥CD.
(2)当点P在上运动时,
①猜想:线段AM与CN有怎样的数量关系,并给出证明.
②求证:PA+PC.
35.(2022秋 杭州期末)如图,BD是矩形ABCD的对角线,,点E,F分别在边AD,BC上,把△ABE和△CDF分别沿直线BE,DF折叠,使点A,C分别落在对角线BD上的点G,H处,连接FG.
(1)求证:BH=DG.
(2)若AB=6,AD=8,求线段FG的长.
(3)若FG∥CD,求的值.
36.(2022秋 上城区期末)如图,E是矩形ABCD边BC上的一点,作DF⊥DE交BA的延长线于点F,连结EF交AD于点G.
(1)求证:△DCE∽△DAF;
(2)已知DC=1,BC=3,
①若G为AD中点,求FG:GE的值;
②若△DGE为等腰三角形,求CE的长.
37.(2022秋 西湖区期末)如图,△ABC内接于⊙O,∠ABC>90°,△ABC的外角∠EAC的平分线交⊙O于点D,连接DB,DC,DB交AC于点F.
(1)求证:△DBC是等腰三角形.
(2)若DA=DF.
①求证:BC2=DC BF.
②若⊙O的半径为5,BC=6,求的值.
38.(2022秋 西湖区校级期末)如图,AB、AC、AD是⊙O中的三条弦,点E在AD上,且AB=AC=AE.连结BC,BD,CD,其中BC交AD于点G.
(1)求证:△ABG∽△ADB.
(2)若∠DBE=α,求∠CAD的度数(用含α的代数式表示).
(3)若AD=15,AB=12,BD=6,求线段CD的长.
39.(2022秋 西湖区校级期末)已知二次函数y=ax2﹣2(a+1)x+4(a≠0).
(1)证明:二次函数的图象与x轴总有交点.
(2)若点P(,b)和点Q(n,b)在该二次函数图象上,求(b)2+n2的值.
(3)将该二次函数图象向下平移2个单位,令新函数图象与x轴的交点横坐标为x1,x2.证明:|x1﹣x2|>2.
40.(2022秋 西湖区期末)在直角坐标系中,设函数y=m(x+1)2+4n(m≠0,且m,n为实数),
(1)求函数图象的对称轴.
(2)若m,n异号,求证:函数y的图象与x轴有两个不同的交点.
(3)已知当x=0,3,4时,对应的函数值分别为p,q,r,若2q<p+r,求证:m<0.
41.(2022秋 上城区期末)二次函数y1=2(x﹣x1)(x﹣x2)(x1,x2是常数)的图象与x轴交于A,B两点.
(1)若A,B两点的坐标分别为(1,0),(2,0),求函数y1的表达式及其图象的对称轴;
(2)若函数y1的图象经过点(2,m),且x1+x2=2时,求m的最大值;
(3)若一次函数y2=kx+b(k,b是常数,k≠0),它的图象与y1的图象都经过x轴上同一点,且x1﹣x2=2.当函数y=y1+y2的图象与x轴仅有一个交点时,求k的值.
42.(2022秋 杭州期末)在平面直角坐标系中,点(1,m),(2,n)在函数y=x2+bx+c(b,c是常数)的图象上.
(1)若m=2,n=3,求该函数的表达式.
(2)若n=3m,求证:该函数的图象经过点.
(3)已知点(3,0),(﹣1,y1),(4,y2)在该函数图象上,若m>0,n<0,试比较y1,y2的大小,并说明理由.
43.(2022秋 杭州期末)已知二次函数y=ax2+bx+c(a>0)的图象经过点A(﹣1,1)和B(2,4).
(1)求a,b满足的关系式.
(2)当自变量x的值满足﹣1≤x≤2时,y随x的增大而增大,求a的取值范围.
(3)若函数图象与x轴无交点,求a2+b2的取值范围.
44.(2022秋 滨江区期末)二次函数y=x2﹣bx+c的图象经过(﹣2,y1),(1,y2)两点.
(1)当b=1时,判断y1与y2的大小.
(2)当y1<y2时,求b的取值范围.
(3)若此函数图象还经过点(m,y1),且1<b<2,求证:3<m<4.
45.(2023秋 杭州期末)综合与实践:问题情境:求方程x2+x﹣1=0的解,就是求二次函数y=x2+x﹣1的图象与x轴交点的横坐标.为了估计这个方程的解,圆圆先取了6个自变量满足x1<x2<x3<x4<x5<x6且x1﹣x2=x2﹣x3=x3﹣x4=x4﹣x5=x5﹣x6,再分别算出相应的y值.列表得:
x的值 x1 x2 x3 x4 x5 x6
y=x2+x﹣1的值 1 0.71 0.44 0.19 0.04 ﹣0.25
操作判断:(1)求x1的值;
实践探究:(2)为了分析函数值的变化规律,圆圆将表格中得到的函数值逐个作差.如:0.71﹣1=﹣0.29,0.44﹣0.71=﹣0.27,得到如下数据:﹣0.29,﹣0.27,﹣0.25,﹣0.15,﹣0.29,通过计算,圆圆发现自己由于粗心算错了其中的一个函数值,请指出算错的是哪一个值,正确的是多少?
问题解决:(3)对于一般的二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的函数值变化进行如表研究:(d≠0)
x的值 x x+d x+2d x+3d x+4d x+5d
y=ax2+bx+c的值 y1 y2 y3 y4 y5 y6
将表格中得到的函数值逐个作差,发现函数值的差与自变量满足某种函数关系,请写出你的发现过程以及发现结论.
46.(2023秋 杭州期末)已知二次函数y=ax2﹣2ax+1(a≠0),图象经过点(﹣1,m),(1,n),(3,p).
(1)当m=﹣2时.
①求二次函数的表达式;
②写出一个符合条件的x的取值范围,使得y随x的增大而增大;
(2)若在m,n,p这三个实数中,只有一个是正数,求证:.
47.(2023秋 拱墅区校级期末)已知二次函数y=x2﹣4x﹣5,点P1(x1,y1)与P2(x2,y2)都在该函数的图象上,且x1+x2=2.
(1)求函数图象的顶点;
(2)若点P1(x1,y1)与P2(x2,y2)与直线x=m的距离恒相等,求m的值;
(3)若y1≥y2,求y1的最小值.
48.(2023秋 滨江区期末)【综合与实践】
【认识研究对象】教材121页给出了如下定义:如图1,如果点P把线段AB分成两条线段AP和PB(AP>PB),且,则我们称点P为线段AB的黄金分割点.类似,我们可以定义:如果一个三角形中,其最长边的长度和最短边的长度的乘积等于第三边长度的平方,那么就称该三角形为“类黄金三角形”.
如图2,已知△ABC是“类黄金三角形”,且AC<AB<BC.若AC=3,BC=5,求AB的长.
【探索研究方法】如图3,已知△ABC是“类黄金三角形”,且AC<AB<BC.
若∠BAC=90°,小滨同学过点A作AD⊥BC于点D,发现了两个结论:
①AB2=BD×BC;
②点D是边BC的黄金分割点;
请给出证明.
【尝试问题解决】小滨同学经历以上探索过程发现:类似问题,可以通过构造相似三角形等方法解决.于是开展新的探究,请解决以下问题:
如图4,已知△ABC是“类黄金三角形”,且AC<AB<BC.若BC=2,∠A=90°∠C,求AB的长.
49.(2023秋 拱墅区期末)综合与实践:
问题背景:借助三角形的中位线可构造一组相似三角形,若将它们绕公共顶点旋转,对应顶点连线的长度存在特殊的数量关系,数学小组对此进行了研究.
如图1,在△ABC中,∠B=90°,AB=BC=4,分别取AB,AC的中点D,E,作△ADE.如图2所示,将△ADE绕点A逆时针旋转,连结BD,CE.
(1)探究发现
旋转过程中,线段BD和CE的长度存在怎样的数量关系?写出你的猜想,并证明.
(2)性质应用
如图3,当DE所在直线首次经过点B时,求CE的长.
(3)延伸思考
如图4,在Rt△ABC中,∠ABC=90°,AB=8,BC=6,分别取AB,BC的中点D,E、作△BDE.将△BDE绕点B逆时针旋转,连接AD,CE.当边AB平分线段DE时,求tan∠ECB的值.
50.(2023秋 上城区期末)综合与实践
探究主题 直角三角板与圆
探究背景 学习了《圆周角》中的推论:“直径所对的圆周角等于90°”后,全班各研究小组用直角三角板开启了数学探究之旅——研究直角三角板的直角顶点在圆上、圆外和圆内三种情况(如图1),具体研究如图1.
探究任务1 找到画直径的简单方法:把直角顶点放在圆上,连接两直角边与圆的两个交点,连两交点的连线是直径.请你说出其中原理: .
探究任务2 用电脑作图工具,对直角顶点在圆外的情况进行动态模拟,发现:无论直角顶点在圆外如何运动,只要两直角边与圆有两个交点,两条直角边所夹的两段弧的度数差不变,为180°.如图2,若∠P=90°,则180°,研究小组对提出的结论进行证明: 证:如图3,连接AC ∵∠ACD,∠CAB, 又∵∠P=∠ACD﹣∠CAB=90°, ∴90°. ∴180°. 探究任务:运用以上研究结论,请用没有刻度的直尺,在图2的圆上截取一段弧等于,根据作图写出结论: .
探究任务3 当直角顶点运动到圆内时如图4,直角∠APD并反向延长两边交圆于B,C两点,形成互相垂直的弦.请观察图4类比探究任务2,对直角及其对顶角所对两段弧的数量关系,提出自己的猜想,并证明. 你的猜想: .(可以用文字描述,也可以结合图形用几何语言描述) 证明:…
探究任务4 各研究小组进行拓展研究比赛,其中高斯研究小组提出问题:如图5,若弦CD⊥AB,BP=3,DP=6,CP=2,求圆的直径. 比赛评分标准如表: 等级评价标准得分☆☆根据条件求出3条以上线段长,但没有求出直径2分☆☆☆☆根据条件求出直径,但没有运用以上探究结论4分☆☆☆☆☆创新运用探究任务4的结论,根据条件求出直径5分
你的解答是:…
51.(2023秋 西湖区期末)定义:由两条与x轴有相同的交点,并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”.
【概念理解】
抛物线y1=2(x﹣1)(x﹣2)与抛物线y2=x2﹣3x+2是否围成“月牙线”?说明理由.
【尝试应用】
抛物线y1(x﹣1)2﹣2与抛物线组成一个如图所示的“月牙线”,与x轴有相同的交点M,N(点M在点N的左侧),与y轴的交点分别为A,B.
①求a:b:c的值.
②已知点P(x0,m)和点Q(x0,n)在“月牙线”上,m>n,且m﹣n的值始终不大于2,求线段AB长的取值范围.
浙江省杭州市近2年各区期末考试压轴题集中训练卷
参考答案与试题解析
一.选择题(共13小题)
1.(2023秋 上城区期末)已知二次函数y=a(x+m﹣1)(x﹣m)(a≠0)的图象上有两点A(x1,y1)和B(x2,y2)(其中x1<x2),则( )
A.若a>0,当x1+x2<1时,a(y1﹣y2)<0
B.若a>0,当x1+x2<1时,a(y1﹣y2)>0
C.若a<0,当x1+x2>﹣1时,a(y1﹣y2)<0
D.若a<0,当x1+x2>﹣1时,a(y1﹣y2)>0
【分析】由二次函数的解析式求得对称轴为直线x,然后判断y1与y2的大小,即可判断每个选项正误.
【解答】解:∵二次函数y=a(x+m﹣1)(x﹣m)(a≠0),
∴y=0时,x1=1﹣m,x2=m,
∴二次函数y=a(x+m﹣1)(x﹣m)的对称轴为直线x,
当a>0时,当x1+x2<1时,
∴,
∴y1>y2,
∴y1﹣y2>0,
∴a(y1﹣y2)>0;
当a<0时,当x1+x2>﹣1时,
∴,
∴当时,y1<y2,
则a(y1﹣y2)>0;
当时,y1>y2,
则a(y1﹣y2)<0;
故选:B.
2.(2023秋 西湖区期末)已知二次函数y=a(x﹣h)2+k(a≠0)的图象与一次函数y=px+q(p≠0)的图象交于(x1,y1)和(x2,y2)两点,则下列结论正确的是( )
A.若a>0,p<0,则x1+x2>2h
B.若x1+x2>2h,则a>0,p<0
C.若a<0,p<0,则x1+x2>2h
D.若x1+x2>2h,则a<0,p<0
【分析】由二次函数解析式可得抛物线对称轴为直线x=h,由函数图象与系数的关系讨论(x1,y1)和(x2,y2)两点中x1+x2与2h的关系.
【解答】解:∵y=a(x﹣h)2+k,
∴抛物线对称轴为直线x=h,
∵a<0,p<0,
∴抛物线开口向下,一次函数中y随x增大而减小,
设x1<x2,则y1>y2,
∴h,
∴x1+x2>2h.
故选:C.
3.(2023秋 拱墅区期末)如图,四边形ABCD内接于⊙O,其中AD>CD,已知对角线AC过点O,对角线BD与CO相交于点E,且AD=BD.若∠BDC=2∠DBC,则( )
A.1 B. C.2 D.3
【分析】令∠DBC的度数为x,进一步表示出∠BDC、∠BAC和∠CAD的度数,利用等边对等角及直径所对的圆周角为90°,可求出x的值,进而发现△ABC是等腰直角三角形及AB与AE相等,即可解决问题.
【解答】解:令∠DBC的度数为x,则∠BDC的度数为2x,
∵,
∴∠BAC=∠BDC=2x,
∵,
∴∠CAD=∠CBD=x,
∴∠BAD=3x.
∵AD=BD,
∴∠DBA=∠DAB=3x.
∵AC为⊙O的直径,
∴∠ABC=90°,
则3x+x=90°,
解得x=22.5°.
∴∠BAC=∠BCA=45°,∠ABE=67.5°,
∴∠AEB=180°﹣45°﹣67.5°=67.5°,
∴AE=AB.
令⊙O的半径为R,
则AB2+CB2=(2R)2,
∵AB=CB,
∴AB,
∴AE=AB,
又∵CE=2R,
∴.
故选:A.
4.(2023秋 滨江区期末)在平面直角坐标系中,已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0),当y≥t时,x≤m﹣1或x≥m+3.若该函数图象过点A(m,5)和B(m+4,q),则q的值可能是( )
A.3 B.4 C.5 D.6
【分析】根据二次函数的性质得出抛物线的开口向上,对称轴为直线x=m+1,然后根据两点到对称轴的距离判断即可.
【解答】解:∵二次函数y=ax2+bx+c(a,b,c是常数,且a≠0),当y≥t时,x≤m﹣1或x≥m+3,
∴抛物线的开口向上,对称轴为直线xm+1,
∵该函数图象过点A(m,5)和B(m+4,q),且m+1﹣m<m+4﹣(m+1),
∴q>5,
故选:D.
5.(2023秋 拱墅区校级期末)如图,AB是⊙O的直径,点C,D在⊙O上,且∠OAC=30°,OD绕着点O顺时针旋转,连接CD交直线AB于点E,当DE=OD时,∠OCE的大小不可能为( )
A.20° B.40° C.70° D.80°
【分析】根据OD绕着点O顺时针旋转,连接CD交直线AB于点E,DE=OD,分三种情况画图进行计算即可.
【解答】解:
连接OC,
①如图1,OD绕着点O顺时针旋转,连接CD交直线AB于点E,
设∠OCE=x,
∵OC=OD,
∴∠OCE=∠D=x,
∵OA=OC,
∴∠OCA=∠A=30°,
∵DE=OD,
∴∠DOE=∠DEO=30°+x+30°=60°+x
∴2(60°+x)+x=180°
解得x=20°.
∴∠OCE的大小为20°;
②如图2,
设∠OEC=x,
∵DE=OD,
∴∠EOD=∠E=x,
∵DO=CO,
∴∠ODC=∠OCD=2x,
∠EOC=2∠A=60°
∴在△OCE中,
x+60°+2x=180°,
解得x=40°,
∴∠OCE=2x=80°;
③如图3,
设∠ACE=x,
∵OA=OC,
∴∠OCA=∠OAC=30°,
∵OC=OD,
∴∠OCD=∠ODC=30°+x,
∵OD=DE
∴∠EODC=15°x,
∴15°x+x=30°
解得x=10°,
∴∠OCE=30°+x=40°.
综上:∠OCE的大小为:20°、40°、80°.
故选:C.
6.(2023秋 杭州期末)如图,正△ABC纸片,E为AC边上的一点,连结BE.将△BAE沿BE翻折得到△BFE,过点C作AB的平行线交EF的延长线于点M,若∠EMC=90° 则的比为( )
A. B. C. D.
【分析】延长ME交AB于点G,设BF交AC于点H,由△ABC是正三角形得∠A=60°,由翻折得∠HFE=∠A=60°,FE=AE,因为CM∥AB,所以∠AGE=∠EMC=90°,可证明△FEH≌△AEG,得∠FHE=∠AGE=90°,则BF⊥AC,∠HEF=30°,则AH=CH,FE=AE=2FH,所以EHFH,可求得EC=(2+2)FH,即可求得,于是得到问题的答案.
【解答】解:延长ME交AB于点G,设BF交AC于点H,
∵△ABC是正三角形,
∴∠A=60°,
由翻折得∠HFE=∠A=60°,FE=AE,
∵CM∥AB,∠EMC=90°,
∴∠AGE=∠EMC=90°,
在△FEH和△AEG中,
,
∴△FEH≌△AEG(ASA),
∴∠FHE=∠AGE=90°,
∴BF⊥AC,∠HEF=90°﹣∠HFE=30°,
∴AH=CH,FE=AE=2FH,
∴EHFH,
∴AH=CH=AE+EH=2FHFH,
∴EC=CH+EH=2FHFHFH=(2+2)FH,
∴,
故选:D.
7.(2023秋 杭州期末)如图,△ABC内接于⊙O,∠ABC>90°,它的外角∠EAC的平分线交⊙O于点D,连接DB,DC,DB交AC于点F.若DA=DF,∠ABC=α,∠DFC=β,则下列结论正确的是( )
A.α+4β=540° B.α+4β=450° C.α+2β=360° D.α+2β=270°
【分析】由∠DAE+∠DAB=180°,∠DCB+∠DAB=180°,得∠DAE=∠DCB,所以∠DAE=∠DAC=∠DBC,则∠DAC=∠DBC=∠DCB,因为DA=DF,所以∠BFC=∠DFA=∠DAC=∠DBC=∠DCB,可证明△DAF∽△DBC,得∠ADB=∠BDC,再由∠ADB=∠ACB,∠BDC=∠BAC,推导出∠ACB=∠BAC,所以∠BDC=∠BAC(180°﹣α),则∠DBC=∠DCB(180°﹣∠BDC)=45°α,因为∠DFC=180°﹣∠BFC=180°﹣∠DBC=135°α,所以β=135°α,则α+4β=540°,可判断A正确,于是得到问题的答案.
【解答】解:∵∠DAE+∠DAB=180°,∠DCB+∠DAB=180°,
∴∠DAE=∠DCB,
∵AD平分∠EAC,
∴∠DAE=∠DAC=∠DBC,
∴∠DAC=∠DBC=∠DCB,
∵DA=DF,
∴∠BFC=∠DFA=∠DAC=∠DBC=∠DCB,
∵∠DAC=∠DBC,∠DFA=∠DCB,
∴△DAF∽△DBC,
∴∠ADB=∠BDC,
∴∠ADB=∠ACB,∠BDC=∠BAC,
∴∠ACB=∠BAC,
∵∠ABC=α,∠DFC=β,
∴∠BDC=∠BAC(180°﹣∠ABC)(180°﹣α),
∴∠DBC=∠DCB(180°﹣∠BDC)=90°(180°﹣α)=45°α,
∵∠DFC=180°﹣∠BFC=180°﹣∠DBC=180°﹣(45°α)=135°α,
∴β=135°α,
∴α+4β=540°,
故A正确,
故选:A.
8.(2022秋 滨江区期末)二次函数y=ax2+4x+1(a为实数,且a<0),对于满足0≤x≤m的任意一个x的值,都有﹣2≤y≤2,则m的最大值为( )
A. B. C.2 D.
【分析】由该二次函数解析式可知,该函数图象的开口方向向下,对称轴为,该函数的最大值为,由题意可解得a≤﹣4,根据函数图象可知a的值越小,其对称轴越靠左,满足y≥﹣2的x的值越小,故令a=﹣4即可求得m的最大值.
【解答】解:∵函数,且a<0,
∴该函数图象的开口方向向下,对称轴为,该函数有最大值,其最大值为,
若要满足0≤x≤m的任意一个x的值,都有﹣2≤y≤2,
则有,解得a≤﹣4,
对于该函数图象的对称轴,a的值越小,其对称轴越靠左,
a的值越小,满足y≥﹣2的x的值越小,
∴当取a的最大值,即a=﹣4时,令y=﹣4x2+4x+1=﹣2,
解得,,
∴满足y≥﹣2的x的最大值为,
即m的最大值为.
故选:D.
9.(2022秋 杭州期末)计算机处理任务时,经常会以圆形进度条的形式显示任务完成的百分比.下面是同一个任务进行到不同阶段时进度条的示意图:
当任务完成的百分比为x时,线段MN的长度记为d(x).下列描述正确的是( )
A.当x1>x2时,d(x1)>d(x2)
B.当d(x1)>d(x2)时,x1>x2
C.当x1+x2=1时,d(x1)=d(x2)
D.当x1=2x2时,d(x1)=2d(x2)
【分析】根据弧,弦和圆心角的关系,利用图象判断即可.
【解答】解:A、当x1>x2时,d(x1)与d(x2)可能相等,可能不等,本选项不符合题意.
B、当d(x1)>d(x2)时,x1>x2或x1<x2,本选项不符合题意.
A、当x1+x2=1时,d(x1)=d(x2),正确,本选项符合题意.
D、当x1=2x2时,d(x1)<2 d(x2)本选项不符合题意.
故选:C.
10.(2022秋 杭州期末)已知点P(m,n),Q(3,0)都在一次函数y=kx+b(k,b是常数,k≠0)的图象上,( )
A.若mn有最大值4,则k的值为﹣9
B.若mn有最小值4,则k的值为﹣9
C.若mn有最大值﹣9,则k的值为4
D.若mn有最小值﹣9,则k的值为4
【分析】由题意得到mn=m(km﹣3k)=k(m2﹣3m)=kk,当k>0mn有最小值,求出k的值,当k<0,mn有最大值,求出k的值,即可解决问题.
【解答】解:∵点P(m,n),Q(3,0)都在一次函数y=kx+b(k,b是常数,k≠0)的图象上,
∴km+b=n,3k+b=0,
∴b=﹣3k,
∴n=km+b=km﹣3k,
∴mn=m(km﹣3k)=k(m2﹣3m)=kk,
当k<0时,mn有最大值k,
若mn有最大值4,k=4,则k,故A不符合题意;
若mn有最大值﹣9,k=﹣9,则k=4,此时k>0,故C不符合题意;
当k>0时,mn有最小值k,
若mn有最小值4,k=4,则k,故B不符合题意;
若mn有最小值﹣9,k=﹣9,则k=4,故D符合题意.
故选:D.
11.(2022秋 上城区期末)如图,AD是△ABC的外角平分线,与△ABC的外接圆交于点D,连结BD交AC于点F,且BC=CF,则下列结论错误的是( )
A.∠ADB=∠CDB B.3∠ACB+∠ACD=180°
C.3∠BDC+2∠ABD=180° D.3∠BAD+∠ABD=360°
【分析】设∠DCB=α,∠BDC=β,表示出有关的角,由圆周角定理,圆内接四边形的性质,可以解决问题.
【解答】解:AD是△ABC的外角平分线,
∴∠EAD=∠DAC,
∵∠EAD=∠DCB,∠DAC=∠DBC,
∴∠DBC=∠DCB,
∵BC=CF,
∴∠FBC=∠CFB,
∴∠BDC=∠BCF,
∵∠ADB=∠BCF,
∴∠ADB=∠BDC.
故A正确,
设∠DCB=α,∠BDC=β,则∠ADB=∠ACB=β,
∴2α+β=180°,
∴3∠ACB+∠ACD=3β+(α﹣β)=α+2β≠180°,
故B错误;
3∠BDC+2∠ABD=3β+2∠ACD=3β+2(α﹣β)=2α+β=180°,
故C正确;
3∠BAD+∠ABD=3(180°﹣α)+(α﹣β)=540°﹣(2α+β)=540°﹣180°=360°,
故D正确;
故选:B.
12.(2022秋 西湖区期末)设函数y1=﹣(x﹣a1)2,y2=﹣(x﹣a2)2.直线x=1的图象与函数y1,y2的图象分别交于点A(1,c1),B(1,c2),得( )
A.若1<a1<a2,则c1<c2 B.若a1<1<a2,则c1<c2
C.若a1<a2<1,则c1<c2 D.若a1<a2<1,则c2<c1
【分析】根据题意分别画出y1,y2的图象,继而根据图象即可求解.
【解答】解:∵直线x=1的图象与函数y1,y2的图象分别交于点A(1,c1),B(1,c2),
A.若1<a1<a2,如图所示,
则c1>c2
B.若a1<1<a2,如图所示,
则c1>c2
则c1<c2,
故B选项不合题意,
C.若a1<a2<1,如图所示,
∴c1<c2,故C选项正确,D选项不正确;
故选:C.
13.(2022秋 西湖区校级期末)如图,将矩形ABCD沿着GE,EC,GF翻折,使得点A,B,D恰好都落在点O处,且点G,O,C在同一条直线上,点E,O,F在另一条直线上.以下结论正确的是( )
A.△COF∽△CEG B.OC=3OF C.AB:AD=4:3 D.GEDF
【分析】先证明GF∥CE,再根据平行线的性质与相似三角形的性质可得FG=FC,可判断A.由矩形的性质设AD=BC=2a,AB=DC=2b,可得,可得,可判断C,设OF=DF=x,可得:,从而可判断D,B,从而可得答案.
【解答】解:由折叠性质可得:DG=OG=AG,AE=OE=BE,OC=BC,∠DGF=∠OGF,∠AGE=∠OGE,∠AEG=∠OEG,∠OEC=∠BEC,
∴∠FGE=∠FGO+∠OGE=90°,∠GEC=∠OEG+∠OEC=90°,
∴∠FGE+∠GEC=180°,
∴GF∥CE,
∴∠FGC=∠GCE,
若△COF∽△CEG,则∠FCO=∠GCE,
∴∠FGC=∠FCO,
∴FG=FC,与题干条件矛盾,故A不符合题意;
由矩形的性质设AD=BC=2a,AB=DC=2b,
由对折可得DG=OG=AG=a,AE=OE=BE=b,
∴CG=OG+OC=OG+BC=3a,
在Rt△CGE中,CG2=GE2+CE2,
∴(3a)2=a2+b2+b2+(2a)2,
解得:,
∴;
∴,故C不符合题意;
在Rt△COF中,设OF=DF=x,
则,
由∠D=∠GOF=90°,
∴,
解得:,
∴,,
在Rt△AGE中,,
∴,故D符合题意;
∴,故B不符合题意;
故选:D.
二.填空题(共12小题)
14.(2023秋 上城区期末)如图,学校要在校园内建一个矩形的开心农场,其中一边AD是围墙,且AD的长不能超过28m,其余三边AB,BC,CD用60m长的铁质栅栏.有下列结论:
①AB的长可以为15m;
②当农场ABCD面积为200m2时,满足条件的AB的长只有一个值;
③农场ABCD面积的最大值为450m2;
④若把农场的形状改成半圆形,且直径一侧利用已有围墙,则农场的面积可以超过560m2.
其中,正确结论的是 ② .(只需填序号)
【分析】依据题意,设AD边长为x m,则AB边长为长为m,当AB=15时,15,解得x=30,故可判断①;当菜园ABCD面积为200m2,由题意得x 200,从而x=30±10,又x≤28,故可判断②;又设矩形菜园的面积为y m2,从而y=x (x﹣30)2+450,结合0,x≤28,从而当x=28时,y有最大值,最大值为448m2不可能为450m2,故可判断③;依据题意,直径一侧是围墙,当直径取最大值28时,半圆的弧长为π×28<60,进而设沿AD方向栅栏延伸a米,则π(28+a)=60﹣a.求得a≈6.2,最后得农场的最大面积为π()2≈459.1<560,故可判断④.
【解答】解:设AD边长为x m,则AB边长为长为m,
当AB=15时,15,
解得x=30,
∵AD的长不能超过28m,
∴x≤28,
故①不正确.
∵菜园ABCD面积为200m2,
∴x 200.
∴x=30±10.
又x≤28,
∴x=30﹣10.
∴满足条件的AB的长只有一个值,故②正确.
由题意,设矩形菜园的面积为y m2,
根据题意得:y=x (x﹣30)2+450,
∵0,x≤28,
∴当x=28时,y有最大值,最大值为448m2不可能为450m2.
故③不正确.
∵直径一侧是围墙,当直径取最大值28时,半圆的弧长为π×28<60,
∴设沿AD方向栅栏延伸a米,则π(28+a)=60﹣a.
∴a≈6.2.
∴农场的最大面积为π()2≈459.1<560.
∴农场的面积不超过560m2.
故④错误.
故答案为:②.
15.(2023秋 西湖区期末)如图,已知AB是⊙O的直径,弦CD⊥AB于点E,OE=BE.点P是劣弧上任意一点(不与点A,D重合),CP交AB于点M,AP与CD的延长线相交于点F,设∠PCD=α.
①则∠F= 60°﹣α ,(用含α的代数式表示);
②当∠F=3∠PCD时,则 .
【分析】①连接OD,BD,PO,由线段垂直平分线的性质得到△ODB是等边三角形,由圆周角定理得到∠A∠POB=30°+α,由直角三角形的性质即可求出∠PFE=60°﹣α.
②设圆的半径是r,OM=x,由∠AFE=3∠PCD,求出α=15°,得到∠POB=90°,因此OP∥CE,推出△POM∽△CEM,得到OM:EM=OP:CE,代入有关数据即可求出OM的长,得到AM,BM的长,即可得到答案.
【解答】解:①连接OD,BD,PO,
∵弦CD⊥AB于点E,OE=BE,
∴OD=BD,
∵OD=OB,
∴△ODB是等边三角形,
∴∠BOD=60°,
∵∠PCD=α,
∴∠POD=2α,
∴∠POB=60°+2α,
∴∠A∠POB=30°+α,
∴∠PFE=90°﹣∠A=60°﹣α.
故答案为:60°﹣α;
②∵∠AFE=3∠PCD,
∴60°﹣α=3α,
∴α=15°,
∴∠POD=2∠PCD=30°,
∴∠POB=90°,
∴OP∥CE,
∴△POM∽△CEM,
∴OM:EM=OP:CE,
∵直径AB⊥CD,
∴DE=CE,
∴OM:EM=OP:ED,
设圆的半径是r,OM=x,
∴EMr﹣x,DEr,
∴x:(r﹣x)=r:r,
∴x=(2)r,
∴OM=(2)r,
∴AM=AO+OM=3rr,BM=OB﹣OMr﹣r,
∴.
故答案为:.
16.(2023秋 拱墅区期末)已知点(3,m),(5,n)在抛物线y=ax2+bx(a,b为实数,a<0)上,设抛物线的对称轴为直线x=t,若n<0<m,则t的取值范围为 t .
【分析】先根据题意得出抛物线与x轴的交点坐标,再由n<0<m即可得出结论.
【解答】解:由题意可知,抛物线与x轴的交点坐标为(0,0),(2t,0),
∵a<0,
∴抛物线开口向下,
∵点(3,m),(5,n)在抛物线y=ax2+bx(a,b为实数,a<0)上,n<0<m,
∴3<2t<5,
∴t.
故答案为:t.
17.(2023秋 滨江区期末)在平面直角坐标系中,二次函数y=ax2+2x+c(a,c是常数,且a≠0)的图象与x轴的一个交点坐标为(﹣2n,0).若该函数图象的顶点坐标为(n,p),则 9 .
【分析】根据抛物线的对称性求得二次函数y=ax2+2x+c(a,c是常数,且a≠0)的图象与x轴的另一个交点坐标为(4n,0),则y=a(x+2n)(x﹣4n)=a(x﹣n)2﹣9an2,由该函数图象的顶点坐标为(n,p)可知n,p=﹣9an2,代入求得即可.
【解答】解:∵函数图象的顶点坐标为(n,p),
∴对称轴为直线x=n,
∵二次函数y=ax2+2x+c(a,c是常数,且a≠0)的图象与x轴的一个交点坐标为(﹣2n,0).
∴二次函数y=ax2+2x+c(a,c是常数,且a≠0)的图象与x轴的另一个交点坐标为(4n,0).
∴y=a(x+2n)(x﹣4n)=a(x﹣n)2﹣9an2,
∴p=﹣9an2,
∴9an,
∴n,
∴9,
故答案为:9.
18.(2023秋 拱墅区校级期末)如图,在Rt△ABC中,∠ACB=90°,把Rt△ABC沿斜边AB折叠,得到△ABD,过点D作DE⊥CA交CA的延长线于点E,过点C作CN∥AD,分别交AB,BD于点M,N,若CM=3,,则 .
【分析】连接DM并延长交BC于点F,首先证明四边形ACMD为平行四边形,AD=CM=3,再证明四边形DFCE为矩形,用勾股定理计算出FM=1,由折叠图形性质、平行线性质及角平分线性质定理可得NM=FM=1,最后证明△BNM∽△BDA,然后根据相似三角形的性质求解.
【解答】解:如图所示,连接DM并延长交BC于点F,
∵CM∥AD,
∴∠DAM=∠CMA,
又由折叠性质可得CA=AD,∠DAM=∠CAM,
∴∠CAM=∠CMA,
∴CA=CM,
∴CM=AD,
∴四边形ACMD为平行四边形,AD=CM=3,
∴DM∥EC,DF∥EC,
又∵∠ECB=90°,
∴∠DFC=90°,
又∵∠E=90°,
∴四边形DFCE为矩形.
∴DE=FC=2,
∴FM1,
由折叠性质可得∠ADB=∠ACB=90°,
又CM∥AD,
∴∠BNM=∠ADB=90°.
又MF⊥BC,BA为∠DBC的角平分线,
∴NM=FM=1,
由MN∥AD,
∴△BNM∽△BDA,
∴,
设BM=k,BA=3k,则AM=3k﹣k=2k,
∴.
故答案为:.
19.(2023秋 杭州期末)数学家菲尔贝提出借助图形代替演算的观点,这类图形称为“诺模图”.如图是关于x,y,z三者关系的诺模图,它是由点O出发的三条射线a,b,c组成,每条射线上都有相同的刻度,且射线端点刻度为0,其中a和c,b和c都相交成60°角.在射线a和b上分别取点A和B,对应的刻度值是x和y.用直尺连结AB交射线c于点C,点C的刻度值就是z的值.
(1)若x=20,y=12,则z的值是 7.5 ;
(2)若x=2y,则 .
【分析】方法一(利用相似三角形):过点C作CD∥OB交OA于点D,先证△OCD为等边三角形得CD=OD=OC=z,进而得AD=x﹣z,再证△ACD和△ABO相似得AD:OA=CD:OB,由此得(x﹣z):x=z:y,然后整理得xz+yz=xy.
(1)将x=20,y=12代入xz+yz=xy之中即可求出z的值;
(2)将x=2y代入xz+yz=xy之中即可求出的值.
解法二(面积法):过点C作CE⊥OA于E,OF⊥OB于F,过B作BH⊥AO交AO的延长线于H,利用三角函数分别求出CE,CF,BH,进而可得S△AOC,S△BOC,S△AOB,然后根据S△AOC+S△BOC=S△AOB,得xz+yz=xy.
(1)将x=20,y=12代入xz+yz=xy之中即可求出z的值;
(2)将x=2y代入xz+yz=xy之中即可求出的值.
【解答】解法一(利用相似三角形):过点C作CD∥OB交OA于点D,如图1所示:
依题意得:∠BOC=∠AOC=60°,OA=x,OB=y,OC=z,
∵CD∥OB,
∴∠OCD=∠BOC=60°,
∴∠OCD=∠AOC=60°,
∴△OCD为等边三角形,
∴CD=OD=OC=z,
∴AD=OA﹣OD=x﹣z,
∵CD∥OB,
∴△ACD∽△ABO,
∴AD:OA=CD:OB,
∴(x﹣z):x=z:y,
整理得:xz+yz=xy,
(1)当x=20,y=12时,20z+12z=20×12,
解得:z=7.5;
故答案为:7.5.
(2)当x=2y时,2yz+yz=2y2,
即3yz=2y2,
∵y≠0,
∴3z=2y,
∴.
故答案为:.
解法二(面积法):过点C作CE⊥OA于E,OF⊥OB于F,过B作BH⊥AO交AO的延长线于H,如图2所示:
依题意得:∠BOC=∠AOC=60°,OA=x,OB=y,OC=z,
在Rt△OCE中,sin∠AOC,
∴CE=OC sin∠AOC=z sin60°,
在Rt△OCF中,sin∠BOC,
∴CF=OC sin∠BOC=z sin60°,
∵∠BOC=∠AOC=60°,
∴∠AOB=120°,
∴∠BOH=180°﹣∠AOB=60°,
在Rt△BOH中,sin∠BOH,
∴BH=OB sin∠BOH=y sin60°,
∴S△AOCOA CE,S△BOCOB CF,S△AOBOA BH,
∵S△AOC+S△BOC=S△AOB,
∴,
∴xz+yz=xy,
(1)当x=20,y=12时,20z+12z=20×12,
z=7.5;
故答案为:7.5.
(2)当x=2y时,2yz+yz=2y2,
即3yz=2y2,
∵y≠0,
∴3z=2y,
∴.
故答案为:.
20.(2023秋 杭州期末)如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,D、E为AB边上两点(点D在点E的右侧),满足∠DCE=45°,则AB边上的高为 ;设AD=x,BE=y.用含x的代数式表示y= .
【分析】利用面积法可求出AB边上的高,旋转△ACD,利用“角含半角”模型构造出全等三角形,再借助于勾股定理即可解决问题.
【解答】解:过点C作AB的垂线,垂足为M,
∵∠ACB=90°,AC=3,BC=4,
∴AB.
又∵,
∴.
即AB边上的高为.
将△ACD绕点C顺时针旋转90°,点A的对应点为点F,点D的对应点为H,延长HF交AB于点G,连接EH,
由旋转可知,
△CHF≌△CDA,
∴∠HCF=∠DCA,HF=AD=x,CF=AC=3,∠HFC=∠A,CH=CD.
又∵∠HFC=∠BFG,∠A+∠B=90°,
∴∠B+∠BFG=90°,
则FG⊥BE.
又∵BF=4﹣3=1.
∴sinB,
则FG.
同理可得,BG.
∴HG=x,EG=y.
∵∠DCE=45°,
∴∠ACD+∠BCE=45°,
∴∠HCE=∠HCF+∠BCE=45°,
∴∠HCE=∠DCE.
在△HCE和△DCE中,
,
∴△HCE≌△DCE(SAS),
∴HE=DE=5﹣x﹣y.
在Rt△HGE中,
(x)2+(y)2=(5﹣x﹣y)2,
整理得,
y.
故答案为:,.
21.(2022秋 滨江区期末)如图,正五边形ABCDE的对角线AC和AD分别交对角线BE于点M,N,若△AMN的面积为s,则正五边形ABCDE的面积为 (结果用含s的代数式表示).
【分析】由正五边形的性质可得,△AMN∽△BAN∽△ACD,设AB=a,表示出解得AMa,则MN=aaa,得出S△ABMs,同理求出S△ACDs,从而解决问题.
【解答】解:由正五边形的性质可知,AB=BC=CD=DE=AE,AM=AN=BM=NE,
由正五边形的性质可得,△AMN∽△BAN∽△ACD,
设AB=a,
∵△AMN∽△BAN,
∴,
即,
解得AMa,
∴MN=aaa,
∴,
∴S△ABMs,
∵△AMN∽△ACD,
∴()2,
∴S△ACDs,
∴S正五边形ABCDE=S△ACD+4S△ABM+2S△AMN
s+4s+2s
,
故答案为:.
22.(2022秋 杭州期末)如图,在正方形ABCD中,点E在边BC上(不与点B,C重合),点F在边CD的延长线上,DF=BE,连接EF交AD于点G,过点A作AN⊥EF于点M,交边CD于点N.若DN=2CN,BE=3.则CN= 5 ,AM= 3 .
【分析】连接AE,AF,EN,由正方形的性质可得AB=AD,BC=CD,∠ABE=∠BCD=∠ADF=90°,可证得△ABE≌△ADF(SAS),可得∠BAE=∠DAF,AE=AF,从而可得∠EAF=90°,根据等腰三角形三线合一可得点M为EF中点,由AN⊥EF可证得△AEM≌△AFM(SAS),△EMN≌△FMN(SAS),可得EN=FN,设CN=x,构建方程求解.
【解答】解:如图,连接AE,AF,EN,
∵四边形ABCD为正方形,
∴AB=AD,BC=CD,∠ABE=∠BCD=∠ADF=90°,
∵BE=DF,
∴△ABE≌△ADF(SAS),
∴∠BAE=∠DAF,AE=AF,
∴∠EAF=90°,
∴△EAF为等腰直角三角形,
∵AN⊥EF,
∴EM=FM,∠EAM=∠FAM=45°,
∴△AEM≌△AFM(SAS),△EMN≌△FMN(SAS),
∴EN=FN,
设CN=x,则DN=2x,BC=CD=3x,
∴EN=FN=DN+DF=2x+3,CE=BC﹣BE=3x﹣3,
在Rt△ECN中,由勾股定理可得:
CN2+CE2=EN2,
即x2+(3x﹣3)2=(2x+3)2,
解得x=5,
∴CN=5,EC=12,CF=18,
∴EF6,
∴AMEF=3.
故答案为:5,3.
23.(2022秋 上城区期末)如图,在矩形ABCD中,AD=4AB.将矩形ABCD对折,得到折痕MN;沿着CM折叠,点D的对应点为E,ME与BC的交点为F;再沿着MP折叠,使得AM与EM重合,折痕为MP,此时点B的对应点为G,则 .
【分析】由矩形及折叠的性质得∠MNC=∠PNM=90°,CN=DM=2DC=2MN,由∠PME∠AME,∠CME∠DME,可推导出∠PMC=90°,则∠MCN=∠PMN=90°﹣∠CMN,即可证明△MNC∽△PNM,得2,即可证明PNPC,再证明∠FMP=∠AMP=∠FPM,∠FMC=∠DMC=∠FCM,则PF=MF=CFPC,所以NF=PF﹣PNPC,即可求得.
【解答】解:∵四边形ABCD是矩形,
∴AB=DC,∠D=∠DCN=90°,AD∥BC,
∴AD=4AB=4DC,
∵将矩形ABCD对折,得到折痕MN,
∴DM=AMAD4DC=2DC,∠MNC=∠PNM=90°,
∴四边形CDMN是矩形,
∴DC=MN,
∴CN=DM=2DC=2MN,
∴∠PME=∠PMA∠AME,∠CME=∠CMD∠DME,
∴∠PMC=∠PME+∠CME(∠AME+∠DME)180°=90°,
∴∠MCN=∠PMN=90°﹣∠CMN,
∴△MNC∽△PNM,
∴2,
∴MN=2PN,CN=2MN,
∴CN=4PN,
∴PNPC,
∵∠FMP=∠AMP=∠FPM,∠FMC=∠DMC=∠FCM,
∴PF=MF=CFPC,
∴NF=PF﹣PNPCPCPC,
∴,
故答案为:.
24.(2022秋 西湖区期末)如图,线段AB是⊙O的直径,弦CD⊥AB于点H,点M是弧BC上任意一点(不与B,C重合),AH=1,CH=2.延长线段BM交DC的延长线于点E,直线MH交⊙O于点N,连结BN交CE于点F,则OC= 2.5 ,HE HF= 4 .
【分析】连接OC,设OC=r,在Rt△COH中,利用勾股定理求出OC;由△EHM∽△NHF,推出,推出HE HF=HM HN,又HM HN=AH HB,推出HE HF=AH HB,由此即可解决问题.
【解答】解:连接OC.
∵CD⊥AB,
∴∠CHO=90°,
设OC=r,则OH=r﹣1,
在Rt△COH中,
∵CH=2,
∴r2=22+(r﹣1)2,
∴r=2.5,即OC=2.5;
连接AM.
∵AB是直径,
∴∠AMB=90°,
∴∠MAB+∠ABM=90°,
∵∠E+∠ABM=90°,
∴∠E=∠MAB,
∴∠MAB=∠MNB=∠E,
∵∠EHM=∠NHF,
∴△EHM∽△NHF,
∴,
∴HE HF=HM HN,
∵HM HN=AH HB,
∴HE HF=AH HB=1×(5﹣1)=4,
故答案为:2.5,4.
25.(2022秋 西湖区校级期末)已知关于x的一元二次方程(x﹣2)(x﹣3)=m有实根x1,x2,且x1<x2,现有下列说法:①当m=0时,x1=2,x2=3;②当m>0时,2<x1<x2<3;③m;④二次函数y=(x﹣x1)(x﹣x2)﹣m的图象与x轴的交点坐标为(2,0)和(3,0).其中正确的有 ①③ .
【分析】解一元二次方程(x﹣2)(x﹣3)=0,根据一元二次方程根与系数的关系即可求解.
【解答】解:①当m=0时,一元二次方程为(x﹣2)(x﹣3)=0,
∴x1=2,x2=3,故①正确;
②当m>0时,
∵一元二次方程(x﹣2)(x﹣3)=m有实根x1,x2,且x1<x2,
∴原方程转化为x2﹣5x+6﹣m=0,
根据根与系数的关系得,,,
若2<x1<x2<3,则|x2﹣x1|<1,
∵,且m>0,
∴|x2﹣x1|<1错误,即2<x1<x2<3错误,故②错误;
∴当m>0时,x<2或x>3,故②错误;
③(x﹣2)(x﹣3)=m转化为x2﹣5x+6﹣m=0,有实根x1,x2,且x1<x2,
∴Δ=b2﹣4ac=(﹣5)2﹣4(6﹣m)>0,即1+4m>0,
∴,故③正确;
④∵一元二次方程(x﹣2)(x﹣3)=m有实根x1,x2,且x1<x2,
∴原方程转化为x2﹣5x+6﹣m=0,
根据根与系数的关系得,,,
∴,即y=x2﹣5x+6﹣2m,
∴由二次函数y=(x﹣x1)(x﹣x2)﹣m的图象与x轴的交点坐标不是(2,0)和(3,0),故④错误.
综上所述,正确的有①③,
故答案为:①③.
三.解答题(共26小题)
26.(2023秋 上城区期末)如图,已知△ABC内接于⊙O,AB是直径,点D在⊙O上,OD∥BC,过点D作DE⊥AB,垂足为E,连接CD交OE边于点F.
(1)求证:△DOE∽△ABC;
(2)求证:∠ODF=∠BDE;
(3)连接OC,设△DOE的面积为S1,四边形OCBD的面积为S2,若,用含n的代数式表示.
【分析】(1)根据圆周角定理和垂直求出∠DEO=∠ACB,根据平行得出∠DOE=∠ABC,根据相似三角形的判定得△DOE∽△ABC,根据圆周角定理得出∠A=∠BDC,推出∠ODE=∠BDC即可;
(2)根据圆周角定理和垂直求出∠DEO=∠ACB,根据平行得出∠DOE=∠ABC,根据相似三角形的判定得出结论;
(3)根据△DOE∽△ABC,求出S△ABC=4S△DOE=4S1,进而求解.
【解答】(1)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD∥BC,
∴∠DOE=∠ABC,
∴△DOE∽△ABC;
(2)证明:∵AB是⊙O的直径,
∴∠ACB=90°,
∵DE⊥AB,
∴∠DEO=90°,
∴∠DEO=∠ACB,
∵OD∥BC,
∴∠DOE=∠ABC,
∴△DOE∽△ABC;
∴∠ODE=∠A,
∵∠A和∠BDC是所对的圆周角,
∴∠A=∠BDC,
∴∠ODE=∠BDC,
∴∠ODF=∠BDE;
(3)解:∵△DOE∽△ABC,
∴()2,
即S△ABC=4S△DOE=4S1,
∵OA=OB,
∴S△BOCS△ABC,即S△BOC=2S1,
∵,S2=S△BOC+S△DOE+S△DBE=2S1+S1+S△DBE,
∴S△DBES1,
∴BE=()OE,
即OEOBDO,
∴sinA=sin∠ODE.
27.(2023秋 西湖区期末)如图,E是正方形ABCD边BC上一个动点(不与B,C重合),F是CD延长线上一点,且DF=BE,连接AE,AF,EF.
(1)求证:△AEF为等腰直角三角形.
(2)过点A作EF的垂线,与直线EF,BC分别交于G,H两点,记∠DFE=α,EF交AD于点I.
①当α=30°,AI=2,求线段AE的长.
②设,△AGI的面积记作S1,△HGE的面积记作S2,用含k的代数式表示.
【分析】(1)证明Rt△ADF≌△ABE,从而∠DAF=∠BAE,AF=AE,进一步得出结论;
(2)①可得出∠GAI=∠DFE=30°,解直角三角形AGI求得AG,解直角三角形AGF求得AF,进而得出AE;
②根据tan∠GAI=tan∠DFE得出,进而得出,可证得△AGI∽△HGE,进而求得结果.
【解答】(1)证明:∵正方形ABCD边,
∴AD=AB,∠ADF=∠ADC=∠B=90°,
∵DF=BE,
∴Rt△ADF≌△ABE(HL),
∴∠DAF=∠BAE,AF=AE,
∴∠DAF+∠DAE=∠BAE+∠DAE=∠ABC=90°,
∴∠EAF=90°,
∴△AEF为等腰直角三角形;
(2)解:①∵AH⊥EF,
∴∠AGF=90°,
∵∠ADF=90°,
∴∠AGF=∠ADF,
∵∠GIA=∠DIF,
∴∠GAI=∠DFE=30°,
∴GI=AI cos30°=2,
由(1)知:△AEF是等腰直角三角形,
∴∠AEF=∠AFE=45°,
∴AF;
②由①知:∠GAI=∠DFE,
∴tan∠GAI=tan∠DFE,
∴,
由①知:∠AEF=45°,
∴tan∠AEF,
∴AG=EG,
∴,
∵四边形ABCD是正方形,
∴AD∥CB,
∴△AGI∽△HGE,
∴.
28.(2023秋 拱墅区期末)如图,四边形ABCD内接于⊙O,对角线AC平分∠BAD,连接BD交AC于点E.
(1)求证:△ABC∽△BEC.
(2)若AB=AC,设△ABD的面积为S1,△BCD的面积为S2,BE=6,EC=4,求的值.
(3)求证:AC2=BC2+AB AD.
【分析】(1)根据圆周角定理可得∠CBD=∠CAD,由角平分线定义得∠BAC=∠CAD,即可证得结论;
(2)过点A作AF⊥BD于点F,过点C作CG⊥BD于点G,可证得△CAB∽△CBE,可得,即,求得AE=5,再证得△AEF∽△CEG,即可求得答案;
(3)先证明△ACB∽△ADE,可得AC AE=AB AD,即AC2﹣AC CE=AB AD,再证得△CBE∽△CAB,可得AC CE=BC2,即可证得结论.
【解答】(1)证明:∵四边形ABCD是圆内接四边形,
∴∠CBD=∠CAD,
∵AC平分∠BAD,
∴∠BAC=∠CAD,
∴∠CBD=∠BAC,
∴△ABC∽△BEC.
(2)解:如图,过点A作AF⊥BD于点F,过点C作CG⊥BD于点G,
∵AB=AC,
∴∠ABC=∠ACB,
∵AC平分∠BAD,
∴∠BAC=∠CAD,
∴,
∴∠BAC=∠CBD,
∴△CAB∽△CBE,
∴∠BEC=∠ABC=∠ACB,,
又∵BE=6,EC=4,
∴BC=BE=6,
∴,
∴AE=5,
∵AF⊥BD,CG⊥BD,
∴∠AFE=∠CGE=90°,
∵∠AEF=∠CEG,
∴△AEF∽△CEG,
∴,
∴.
(3)证明:∵AC平分∠BAD,
∴∠BAC=∠CAD,
∵,
∴∠ACB=∠ADB,
∴△ACB∽△ADE,
∴,
∴AC AE=AB AD,
∴AC (AC﹣CE)=AB AD,
∴AC2﹣AC CE=AB AD,
∵,
∴∠CBD=∠BAC,
∵∠BCE=∠ACB,
∴△CBE∽△CAB,
∴,
∴AC CE=BC2,
∴AC2﹣BC2=AB AD,
即AC2=BC2+AB AD.
29.(2023秋 滨江区期末)如图,在⊙O中,弦AB是直径,点C,D是⊙O上的两点,连结AC,OD,且满足AC∥OD.
(1)若的度数为80°,求∠A的度数.
(2)求证:.
(3)连结BD,若AC=6,AB=10,求BD的长.
【分析】(1)连接OC,根据弧AC的度数求出∠AOC,利用三角形内角和求出∠A;
(2)利用平行线的性质求得∠BOD=∠A=50°,∠COD=∠OCA=50°,得出∠COD=∠BOD,进而得出弧相等;
(3)先根据勾股定理求出BC,然后利用勾股定理求出OE,再利用勾股定理求出BD即可.
【解答】(1)解:连接OC,
∵的度数为80°,
∴∠AOC=80°,
∵OA=OC,
∴∠A=∠OCA=50°;
(2)证明:∵AC∥OD,
∴∠BOD=∠A,∠COD=∠OCA,
∵OA=OC,
∴∠A=∠OCA,
∴∠COD=∠BOD,
∴;
(3)解:连接BC,交OD于点E,
∵弦AB是直径,
∴∠ACB=90°,
∵AC=6,AB=10,
∴BC8,
∵,
∴OD⊥BC,
∴CE=BE=4,
∴OE3,
∴DE=OD﹣OE=2,
∴BD2.
30.(2023秋 拱墅区校级期末)如图,已知正方形ABCD的边长为12,点E是射线BC上一点(点E不与点B、C重合),过点A作AF⊥AE,交边CD的延长线于点F,直线EF分别交射线AC、射线AD于点M、N.
(1)求证:△ABE≌△ADF;
(2)当点E在边BC上时,如果AN=5DN,求∠BAE的正切值.
(3)当点E在边BC延长线上时,设线段BE=x,y=EN MF,求y关于x的函数解析式.
【分析】(1)根据正方形的性质得AB=AD,∠B=∠ADC=90°=∠ADF,根据同角的与角相等得∠BAE=∠DAF,利用ASA即可得△ABE≌△ADF;
(2)根据全等三角形、相似三角形的性质以及锐角三角函数的定义进行计算即可;
(3)利用等腰三角形的性质,相似三角形的性质得出EN MF=AE2,再根据勾股定理得出AE2=36+x2即可.
【解答】(1)证明:∵四边形ABCD是正方形,
∴AB=AD=12,∠B=∠ADC=90°=∠ADF,
∵AE⊥AF,
∴∠EAF=90°=∠DAF+∠DAE,
∵∠BAE+∠DAE=∠BAD=90°,
∴∠BAE=∠DAF,
∴△ABE≌△ADF(ASA);
(2)解:∵△ABE≌△ADF,
∴AE=AF,DF=BE,
∵AN=5DN,AD=12=DN+AN,
∴DN=2,AN=10,
∵DN∥EC,
∴,
设BE=x,则DF=x,EC=12﹣x,
∴,
解得x=4或x=6,
经检验,x=4,x=6都是原方程的根,
∴BE=4或BE=6,
在Rt△ABE中,
tan∠BAE或tan∠BAE,
∴∠BAE的正切值为或;
(3)如图,
由(1)得AE=AF,
∵AE⊥AF,
∴△AEF是等腰直角三角形,
∴∠AEF=∠AFE=45°,
∵∠AEF=45°=∠MAN,∠M=∠M,
∴△MAN∽△MFA,
∴∠ANE=∠MAF,
∴△ANE∽△MAF,
∴,
∴EN MF=AE AF=AE2,
在Rt△ABE中,AB=12,BE=x,
∴AE2=AB2+BE2=144+x2,
∴y=EN MF,
∴y=144+x2(x>12).
31.(2023秋 杭州期末)如图,⊙O是Rt△ABC的外接圆,点D是弧AB的中点,过点D作AB的平行线交CA的延长线于点E,连结BD,BE.
(1)求证:∠EDC=∠DBC;
(2)当CD=2时,求S△BCE的值;
(3)设BC=nAC.
①求的值;(用含n的代数式表示)
②若3CE=8AC,DE=6,求AB的长.
【分析】(1)连接AD,利用平行线的性质,同弧作对的圆周角相等,通过等量代换证明即可;
(2)通过证明△CDE∽△CBD,求出BC CE=4,即可求三角形的面积;
(3)①过D点作DG⊥AE交于G点,由题可得tan∠CAB=n,设GE=a,则GD=na,分别求出CDna,CE=a+na,BC,再由△CDE∽△CBD,得到,;
②由①可知BC,则AC,则AB,根据题意分别得到36=a2(1+n2),3(a+na)=8 ,求出n=3或n,再求AB的长即可.
【解答】(1)证明:连接AD,
∵ED∥AB,
∴∠ADE=∠BAD,
∵点D是弧AB的中点,
∴∠CDB=∠ECD,
∵∠ACB=90°,
∴∠BCD=45°,
∵,
∴∠BCD=∠BAD,
∵,
∴∠ACD=∠CBA,
∴∠EDC=∠CBD;
(2)解:∵∠ECD=∠BCD,∠EDC=∠CBD,
∴△CDE∽△CBD,
∴CD2=BC CE,
∵CD=2,
∴BC CE=4,
∴S△BCEBC CE=2;
(3)①解:过D点作DG⊥AE交于G点,
∵BC⊥AE,
∴DG∥BC,
∴∠CED=∠ACB,
∵BC=nAC,
∴tan∠CAB=n,
设GE=a,则GD=na,
∵∠ACB=45°,
∴CG=GD=na,
∴CDna,CE=a+na,
∵CD2=BC CE,
∴2n2a2=(a+na)BC,
解得BC,
∵△CDE∽△CBD,
∴,
∴;
②解:由①可知BC,则AC,
∴AB,
∵DE6,
∴36=a2(1+n2),
∵3CE=8AC,
∴3(a+na)=8 ,
解得n=3或n,
当n=3时,a,则AB=9;
当n时,a,则AB=3;
综上所述:AB=9或3.
32.(2023秋 杭州期末)如图1,在△ABC中,AB=AC,∠A=90°,点P是△ABC内一个动点,且∠BPC=135°.
(1)试找出与∠ACP相等的角,并说明理由;
(2)如图2,连接AP并延长交△BPC的外接圆⊙O于点Q,交BC于点D,连接CQ.
①求证△ACP∽△AQC;
②求的最小值;
(3)在如图2的条件下,若BP=PC,求证:.
【分析】(1)根据∠ACB=∠ACP+∠BCP=45°,∠PBC+∠PCB=45°,等量代换即可得到∠ACP=∠PBC;
(2)①根据同弧所对的圆周角相等,结合(1)能得到∠Q=∠APC,即可证明;
②连接OB、CO,由△ACP∽△AQC,得到,当CQ经过圆心O时,的值最小,过点O作OM⊥BC交于M点,则M是BC的中点,连接AM,则A、O、M三点共线,则AO是BC的垂直平分线,再由CO=AC,得到CQ=2AC,即可求的最小值为;
(3)由题意可知P点AM上,则∠PBC=∠PCB=∠ACP,过点P作PH⊥AC交于H点,设PM=x,则PH=x,分别求出APx,AM=(1)x,AC(1)x,PC2=(4+2)x2,再由,即可证明.
【解答】(1)解:∵∠BPC=135°,
∴∠PBC+∠PCB=45°,
∵AB=AC,∠A=90°,
∴∠ACB=∠ACP+∠BCP=45°,
∴∠ACP=∠PBC;
(2)①证明:∵,
∴∠Q=∠PBC,
∵∠ACP=∠PBC,
∴∠Q=∠APC,
∴△ACP∽△AQC;
②连接OB、CO,
∵∠BPC=135°,
∴∠BOC=90°,
∵△ACP∽△AQC,
∴,
∴,
当CQ经过圆心O时,的值最小,
过点O作OM⊥BC交于M点,则M是BC的中点,连接AM,则A、O、M三点共线,
∴AO是BC的垂直平分线,
∵AM=BM=OM,
∴CO=AC,
∴CQ=2AC,
∴的最小值为;
(3)证明:∵BP=PC,
∴P点AM上,
∴∠PBC=∠PCB=∠ACP,
过点P作PH⊥AC交于H点,
∴PH=PM,
设PM=x,则PH=x,
∵∠PAH=45°,
∴APx,
∴AM=(1)x,AC(1)x,PC2=(4+2)x2,
∵,
∴()2,
∴CQ2=(2)AC2.
33.(2022秋 滨江区期末)如图1,在⊙O中,AB为弦,CD为直径,且AB⊥CD于点E,过点B作BF⊥AD,交AD的延长线于点F.连接AC,BO.
(1)求证:∠CAE=∠ADC.
(2)若DE=2OE,求的值.
(3)如图2,若BO的延长线与AC的交点G恰好为AC的中点,若⊙O的半径为r.求图中阴影部分的面积(结果用含r的代数式表示).
【分析】(1)由圆周角定理可得∠CAD=∠CAE+∠DAE=90°,再根据AB⊥CD,易得∠ADC+∠DAE=90°,即可证明∠CAE=∠ADC;
(2)连接BD,设OE=a,则DE=2a,OB=OD=3a,由勾股定理可得,,再证明△BOE∽△BDF,由相似三角形的性质可得,代入数值可求得,即可获得答案;
(3)连接BD,首先证明△OBE≌△DAE,结合全等三角形的性质进一步证明△OBD为等边三角形,即有∠BOD=60°;利用勾股定理、等边三角形的性质以及含30度角的直角三角形的性质依次求得OE、BE、AB、BF、AF等的值,然后由S阴影=S△ABF﹣S△DAE﹣(S扇形OBD﹣S△OBE)即可获得答案.
【解答】解:(1)∵CD为⊙O直径,
∴∠CAD=90°,即∠CAE+∠DAE=90°,
又∵AB⊥CD,
∴∠ADC+∠DAE=90°,
∴∠CAE=∠ADC;
(2)如图,连接BD,
∵AB⊥CD,DE=2OE,
∴OD=DE+OE=3OE,
设OE=a,则DE=2a,OB=OD=3a,
∴在Rt△OBE中,,
∴在Rt△DBE中,,
∵CD为⊙O直径,且AB⊥CD,
∴BE=AE,
∴AD=BD,
∴∠DAB=∠DBA,
∴∠BDF=∠DAB+∠DBA=2∠DAB,
又∵,
∴∠DOB=2∠DAB=∠BDF,
∵∠OEB=∠DFB=90°,
∴△BOE∽△BDF,
∴,即,
解得,
∴;
(3)如图,连接BD,
∵BO的延长线与AC的交点G恰好为AC的中点,
∴OG⊥AC,即∠OGC=∠CAD=90°,
∴BG∥AD,
∴∠OBE=∠DAE,
又∵BE=AE,∠OEB=∠DEA,
∴△OBE≌△DAE(ASA),
∴OB=DA,
∵CD为⊙O直径,AB⊥CD,
∴,
∴DA=DB,
∴OD=OB=DB,即△OBD为等边三角形,∠BOD=60°,
∵⊙O的半径为r,
∴OB=r,,
∴,
∴,
∵,
∴,
∴,
∴,
∵△OBE≌△DAE,
∴S△OBE=S△DAE,
∴S阴影=S△ABF﹣S△DAE﹣(S扇形OBD﹣S△OBE)
=S△ABF﹣S扇形OBD
.
34.(2022秋 杭州期末)如图,⊙O的半径为1,直径AB,CD的夹角∠AOD=60°,点P是上一点,连接PA,PC分别交CD,AB于点M,N.
(1)若PC⊥AB,求证:PA⊥CD.
(2)当点P在上运动时,
①猜想:线段AM与CN有怎样的数量关系,并给出证明.
②求证:PA+PC.
【分析】(1)由圆周角定理得出∠BAP=30°,由三角形内角和定理可求出∠AMO=90°,则可得出结论;
(2)①连接AD,证出∠D=60°,OA=AD=OD,证明△ADM≌△CON(ASA),由全等三角形的性质得出AM=CN;
②证明△AOM∽△APN,由相似三角形的性质得出,证明△CON∽△CPM,由相似三角形的性质得出,由全等三角形的性质得出AM=CN,DM=ON,代入PA+PC并化简整理可得出答案.
【解答】(1)证明:∵∠AOD=∠BOC=60°,PC⊥AB,
∴60°,
∴∠BAP=30°,
∴∠AMO=180°﹣∠MAO﹣∠AOM=180°﹣30°﹣60°=90°,
∴PA⊥CD;
(2)解:①AM=CN.
证明:连接AD,
∵OA=OD,∠AOD=60°,
∴△OAD是等边三角形,
∴∠D=60°,OA=AD=OD,
∵OC=OD,∠BOC=∠AOD=60°,
∴AD=OC,∠D=∠BOC=60°,
又∵∠DAP=∠DCP,
∴△ADM≌△CON(ASA),
∴AM=CN;
②证明:∵⊙O的半径为1,
∴OA=OB=OC=OD=1,
∵∠P=∠D=60°,∠AOD=60°,
∴∠P=∠AOD,
又∵∠BAP=∠BAP,
∴△AOM∽△APN,
∴,
∴,即PA,
∵∠BOC=∠CPM=60°,∠C=∠C,
∴△CON∽△CPM,
∴,
∴PC,
∵△ADM≌△CON,
∴AM=CN,DM=ON,
又∵DM+OM=OD=1,
∴PA+PC.
35.(2022秋 杭州期末)如图,BD是矩形ABCD的对角线,,点E,F分别在边AD,BC上,把△ABE和△CDF分别沿直线BE,DF折叠,使点A,C分别落在对角线BD上的点G,H处,连接FG.
(1)求证:BH=DG.
(2)若AB=6,AD=8,求线段FG的长.
(3)若FG∥CD,求的值.
【分析】(1)根据矩形性质可得AB=CD,由折叠得:BG=AB,DH=CD,推出BG=DH,即可证得结论;
(2)利用勾股定理可得BD=10,设FH=CF=x,利用S△CDF+S△BDF=S△BCD,建立方程可求得x=3,再利用勾股定理即可求得答案;
(3)由相似三角形性质可得出,设k,AB=a,则BC=k AB=ka,AD=BC=ka,利用勾股定理可得BDa,再利用折叠性质可得DG,由BG+DG=BD,可得aa,解得:k2,即可求得答案.
【解答】(1)证明:∵四边形ABCD是矩形,
∴AB=CD,
由折叠得:BG=AB,DH=CD,
∴BG=DH,
∴BD﹣DH=BD﹣BG,
即BH=DG.
(2)解:∵四边形ABCD是矩形,
∴∠A=∠C=90°,AB=CD,AD=BC,
∵AB=6,AD=8,
∴BD10,
∵BG=DH=AB=6,
∴GH=BG+DH﹣BD=6+6﹣10=2,
由折叠得:∠DHF=∠C=90°,FH=CF,设FH=CF=x,
∵S△CDF+S△BDF=S△BCD,
∴6x10x6×8,
解得:x=3,
∴FH=3,
在Rt△FGH中,FG,
∴线段FG的长为.
(3)解:∵FG∥CD,
∴△BFG∽△BCD,
∴,
∵AB=CD=BG,
∴,
设k,AB=a,则BC=k AB=ka,AD=BC=ka,
∵,
∴1<k,
∴BDa,
∵FG∥CD,
由折叠得∠FDG=∠FDC,BG=AB=a,
∴∠DFG=∠FDG,
∴DG=FG,
∵,
∴,
∴FG,
∴DG,
∵BG+DG=BD,
∴aa,
解得:k2,
∴,
故的值为.
36.(2022秋 上城区期末)如图,E是矩形ABCD边BC上的一点,作DF⊥DE交BA的延长线于点F,连结EF交AD于点G.
(1)求证:△DCE∽△DAF;
(2)已知DC=1,BC=3,
①若G为AD中点,求FG:GE的值;
②若△DGE为等腰三角形,求CE的长.
【分析】(1)根据矩形的性质、垂直的定义得到∠DAB=∠ADC=∠C=90°=∠DAF,结合邻补角定义推出∠ADF=∠CDE,即可判定△DCE∽△DAF;
(2)①根据相似三角形的性质得出AF=3CE,过点G作GM⊥BC于点M,根据矩形的判定与性质、平行线分线段成比例推出,,据此求解即可;
②分三种情况根据等腰三角形的性质求解即可.
【解答】(1)证明:∵四边形ABCD是矩形,
∴∠DAB=∠ADC=∠C=90°,
∵∠DAF+∠DAB=180°,
∴∠DAF=90°=∠C,
∵DF⊥DE,∠ADC=90°,
∴∠ADF+∠GDE=∠GDE+∠CDE=90°,
∴∠ADF=∠CDE,
∴△DCE∽△DAF;
(2)解:①∵△DCE∽△DAF,
∴,
∵DC=1,BC=AD=3,
∴,
∴AF=3CE,
过点G作GM⊥BC于点M,
∵四边形ABCD是矩形,GM⊥BC,
∴四边形GMCD是矩形,
∴DG=CM,GM=CD=1,
∵G为AD中点,AD=BC,
∴CM=BMBC,
∵∠EMG=∠B=90°,
∴GM∥BF,
∴,
∴,
∴CE或1,
∴EM=1或,
∴或3,,
∴FG:GE的值为或3;
②分以下三种情况:
若DG=GE时,△DGE为等腰三角形,则DG=GE=FG,如图,过点G作GM⊥BC于点M,
∵,
∴1,
∴BM=EM,
∴,
∴,
∴CE;
若DE=GE时,△DGE为等腰三角形,如图,过点G作GM⊥BC于点M,
∵DE=GE,GM=CD,
∴Rt△CDE≌Rt△MGE,
∴EM=CE,
∴BE=3﹣CE,AG=BM=3﹣2CE,
∵AD∥BC,
∴△AFG∽△BFE,
∴,
∴,
∴CE或(舍去);
若DG=DE时,△DGE为等腰三角形,如图,连接BG,
∵DG=DE,
∴∠DGE=∠DEG,
∴AD∥BC,
∴∠DGE=∠GEB=∠DEG,
又∠FDE=∠FBE=90°,EF=EF,
∴△FDE≌△FBE(AAS),
∴DE=BE,
∴DG=DE=BE,
又∵DG∥BE,
∴四边形DGBE是菱形,
∴AG=CE,DG=3﹣CE,
在Rt△CDE中,DE2=CD2+CE2,
∴(3﹣CE)2=12+CE2,
∴CE;
综上,若△DGE为等腰三角形,CE的长为或或.
37.(2022秋 西湖区期末)如图,△ABC内接于⊙O,∠ABC>90°,△ABC的外角∠EAC的平分线交⊙O于点D,连接DB,DC,DB交AC于点F.
(1)求证:△DBC是等腰三角形.
(2)若DA=DF.
①求证:BC2=DC BF.
②若⊙O的半径为5,BC=6,求的值.
【分析】(1)由题意易得∠BCD+∠BAD=180°,则有∠EAD=∠BCD,进而可得∠EAD=∠DAC,则∠BCD=∠CBD,然后问题可求证;
(2)①由题意易证△DAF∽△DBC,则有∠ADF=∠BDC,进而可得∠DFA=∠DCB,再由相似三角形的判定得出△FBC∽△BCD,利用其性质即可证明;
②连接DO交BC于G,由题意易得D、O都在中垂线上,即D、O、G共线,进而可得DO⊥BC且BG=GC=3,则有DG=4+OD=9,由①得,根据相似三角形的性质得出,再由相似三角形的判定得出△AFD∽△BFC,利用其性质即可求解.
【解答】(1)证明:∵四边形ABCD内接于⊙O,
∴∠BCD+∠BAD=180°,
∵∠DAB+∠EAD=180°,
∴∠EAD=∠BCD,
∴∠CAD=∠CBD,
∵AD平分∠EAC,
∴∠EAD=∠DAC,
∴∠BCD=∠CBD,
∴DB=DC,
∴△DBC是等腰三角形;
(2)①证明:∵DA=DF,
∴∠DAF=∠DFA,
∴∠DAF=∠DFA=∠CBD=∠BCD,
∴△DAF∽△DBC,
∴∠ADF=∠BDC,
∴∠DFA=∠DCB,
∵∠DBC=∠FBC,
∴△FBC∽△BCD,
∴,
∴BC2=BD BF,
∵DB=DC,
∴BC2=DC BF;
②解:连接DO交BC于G,
∵BD=DC,OB=OC,
∴D、O都在中垂线上,即D、O、G共线,
∴DO⊥BC且BG=GC=3,
∵OB=5,
∴在Rt△BOG中,OG=4,
∴DG=4+OD=9,
∴在Rt△BDG中,,
∵△FBC∽△BCD,
∴,
∴,
解得:,
∴,
∴,
∵∠DAC=∠DBC,∠DFA=∠BFC,
∴△AFD∽△BFC,
∴,
∴.
38.(2022秋 西湖区校级期末)如图,AB、AC、AD是⊙O中的三条弦,点E在AD上,且AB=AC=AE.连结BC,BD,CD,其中BC交AD于点G.
(1)求证:△ABG∽△ADB.
(2)若∠DBE=α,求∠CAD的度数(用含α的代数式表示).
(3)若AD=15,AB=12,BD=6,求线段CD的长.
【分析】(1)由等弦所对弧相等,再由等弧所对圆周角相等得出∠ABC=∠ADB,又∠BAG=∠DAB,即可得出结论;
(2)由等边对等角的性质与圆周角性质得出∠DBE=∠CBE=α,即可由∠CAD=∠CBD=∠DBE+∠CBE求解;
(3)由△ABG∽△ADB,得,从而可求出,,从而求出,再证△BDG∽△ADC,得,代入即可求解.
【解答】(1)证明:∵AB=AC,
∴,
∴∠ABC=∠ADB,
又∵∠BAG=∠DAB,
∴△ABG∽△ADB;
(2)解:∵AB=AE,
∴∠AEB=∠ABE,
∴∠DBE+∠ADB=∠ABC+∠CBE,
∵AB=AC,,
∴∠ABC=∠ACB=∠ADB,
∴∠DBE=∠CBE=α,
∵,
∴∠CAD=∠CBD=∠DBE+∠CBE=2α;
(3)解:∵△ABG∽△ADB,
∴,
∵AD=15,AB=12,BD=6,
∴,
∴,,
∴,
∵∠CAD=∠CBD=2α,∠ADC=∠GDB,
∴△BDG∽△ADC,
∴,即,
∴.
39.(2022秋 西湖区校级期末)已知二次函数y=ax2﹣2(a+1)x+4(a≠0).
(1)证明:二次函数的图象与x轴总有交点.
(2)若点P(,b)和点Q(n,b)在该二次函数图象上,求(b)2+n2的值.
(3)将该二次函数图象向下平移2个单位,令新函数图象与x轴的交点横坐标为x1,x2.证明:|x1﹣x2|>2.
【分析】(1)计算出△,可以证明△大于等于0,即可说明图象与x轴总有交点;
(2)先求出抛物线对称轴,在根据P,Q关于对称轴对称求出n=2,再把点P坐标代入抛物线求出b=2,再求出(b)2+n2的值;
(3)求出平移后的新函数解析式,再由二次函数与方程的关系证明即可.
【解答】(1)证明:∵Δ=[﹣2(a+1)]2﹣4a×4=4a2+8a+4﹣16a=4a2﹣8a+4=4(a﹣1)2≥0,
∴二次函数的图象与x轴总有交点;
(2)解:∵y=ax2﹣2(a+1)x+4(a≠0),
∴抛物线对称轴为直线x1,
∵点P(,b)和点Q(n,b)关于对称轴对称,
∴1,
∴n=2,
把P(,b)代入函数解析式得:a2(a+1)4=b,
解得b=2,
∴(b)2+n2=(2)2+22=8;
(3)证明:∵将二次函数y=ax2﹣2(a+1)x+4(a≠0)的图象向下平移2个单位,
平移后的解析式为y=ax2﹣2(a+1)x+2,
∵平移后函数图象与x轴的交点横坐标为x1,x2,
∴ax2﹣2(a+1)x+2=0的两个根为x1,x2,
∴x1+x2,x1 x2,
∴|x1﹣x2|2.
40.(2022秋 西湖区期末)在直角坐标系中,设函数y=m(x+1)2+4n(m≠0,且m,n为实数),
(1)求函数图象的对称轴.
(2)若m,n异号,求证:函数y的图象与x轴有两个不同的交点.
(3)已知当x=0,3,4时,对应的函数值分别为p,q,r,若2q<p+r,求证:m<0.
【分析】(1)根据对称轴的定义解答即可;
(2)令y=0,则有,由m,n异号,可知一元二次方程有两个实数根,即函数y的图象与x轴有两个不同的交点;
(3)把x=0,3,4代入y=m(x+1)2+4n表示出p,q,r,再利用2q﹣(p+r)<0,解题即可.
【解答】(1)解:∵函数y=m(x+1)2+4n(m≠0,且m,n为实数),
∴函数图象的对称轴为x=﹣1;
(2)证明:令y=0,则0=m(x+1)2+4n,
即,
∵m,n异号,
∴,
∴一元二次方程有两个不相等的实数根,即函数y的图象与x轴有两个不同的交点;
(3)证明:由题可知p=m+4n,q=16m+4n,r=25m+4n,
∵2q﹣(p+r)=2(16m+4n)﹣(m+4n+25m+4n)=6m<0,
∴m<0.
41.(2022秋 上城区期末)二次函数y1=2(x﹣x1)(x﹣x2)(x1,x2是常数)的图象与x轴交于A,B两点.
(1)若A,B两点的坐标分别为(1,0),(2,0),求函数y1的表达式及其图象的对称轴;
(2)若函数y1的图象经过点(2,m),且x1+x2=2时,求m的最大值;
(3)若一次函数y2=kx+b(k,b是常数,k≠0),它的图象与y1的图象都经过x轴上同一点,且x1﹣x2=2.当函数y=y1+y2的图象与x轴仅有一个交点时,求k的值.
【分析】(1)利用待定系数法解答即可;
(2)将已知条件代入解析式中,得到m关于x1的函数关系式,利用二次函数的性质,配方法解答即可得出结论;
(3)利用分类讨论的思想方法分别得到y关于x1,x2的解析式,再利用待定系数法和已知条件解答即可.
【解答】解:二次函数y1=2(x﹣x1)(x﹣x2)=2x2﹣2(x1+x2)x+2x1x2,
∵二次函数y1=2(x﹣x1)(x﹣x2)经过(1,0),(2,0),
∴,
解得:,
∴函数y1的表达式为y1=2x2﹣6x+4.
∵y1=2x2﹣6x+4=2,
∴函数y1的对称轴为直线x;
(2)∵函数y1的图象经过点(2,m),
∴m=2×22﹣4(x1+x2)+2x1x2=8﹣4(x1+x2)+2x1x2,
∵x1+x2=2,
∴x2=2﹣x1,
∴m=8﹣4×2+2x1 (2﹣x1)
=﹣24x1
=﹣22,
∵﹣2<0,
∴当x1=1时,m有最大值为2.
∴m的最大值为2;
(3)由题意:二次函数y1=2(x﹣x1)(x﹣x2)(x1,x2是常数)的图象与x轴交于(x1,0),(x2,0)两点,
①若两函数的图象都经过x轴上同一点(x1,0),
∴0=kx1+b,
∴b=﹣kx1,
∴y2=kx﹣kx1.
∵y=y1+y2,
∴y=2x2﹣2(x1+x2)x+2x1x2+kx﹣kx1
=2x2﹣(2x1+2x2﹣k)x+2x1x2﹣kx1.
∵函数y=y1+y2的图象与x轴仅有一个交点,
∴Δ=0.
即0,
整理得:0,
∴k=﹣2(x1﹣x2).
∵x1﹣x2=2,
∴k=﹣2×2=﹣4;
②若两函数的图象都经过x轴上同一点(x2,0),
∴0=kx2+b,
∴b=﹣kx2,
∴y2=kx﹣kx2.
∵y=y1+y2,
∴y=2x2﹣2(x1+x2)x+2x1x2+kx﹣kx2
=2x2﹣(2x1+2x2﹣k)x+2x1x2﹣kx2.
∵函数y=y1+y2的图象与x轴仅有一个交点,
∴Δ=0.
即4×2(2x1x2﹣kx2)=0,
整理得:0,
∴k=2(x1﹣x2).
∵x1﹣x2=2,
∴k=2×2=4.
综上,当函数y=y1+y2的图象与x轴仅有一个交点时,k的值为4或﹣4.
42.(2022秋 杭州期末)在平面直角坐标系中,点(1,m),(2,n)在函数y=x2+bx+c(b,c是常数)的图象上.
(1)若m=2,n=3,求该函数的表达式.
(2)若n=3m,求证:该函数的图象经过点.
(3)已知点(3,0),(﹣1,y1),(4,y2)在该函数图象上,若m>0,n<0,试比较y1,y2的大小,并说明理由.
【分析】(1)把(1,2),(2,3)分别代入y=x2+bx+c中得到关于b、c的方程组,然后解方程组即可;
(2)把(1,m),(2,3m)分别代入y=x2+bx+c中得到关于b、c的方程组,解方程组得到抛物线解析式为y=x2+(2m﹣3)x+2﹣m,然后计算x时,y,从而可判断抛物线经过点(,);
(3)如图,由于x=1时,y>0;x=2时,y<0,抛物线经过点(3,0),则可判断抛物线的对称轴在直线x=2的右侧,在直线x=3的左侧,然后利用点(﹣1,y1)到对称轴的距离大于点(4,y2)到对称轴的距离,从而得到y1>y2.
【解答】(1)解:把(1,2),(2,3)分别代入y=x2+bx+c得,
解得,
∴抛物线解析式为y=x2﹣2x+3;
(2)证明:把(1,2),(2,3)分别代入y=x2+bx+c得,
解得,
∴抛物线解析式为y=x2+(2m﹣3)x+2﹣m,
∵当x时,y(2m﹣3)+2﹣m,
∴抛物线经过点(,);
(3)y1>y2.
理由如下:
如图,
∵m>0,n<0,
∴x=1时,y>0;x=2时,y<0,
∵抛物线经过点(3,0),
∴抛物线的对称轴在直线x=2的右侧,在直线x=3的左侧,
∴点(﹣1,y1)到对称轴的距离大于点(4,y2)到对称轴的距离,
而抛物线开口向上,
∴y1>y2.
43.(2022秋 杭州期末)已知二次函数y=ax2+bx+c(a>0)的图象经过点A(﹣1,1)和B(2,4).
(1)求a,b满足的关系式.
(2)当自变量x的值满足﹣1≤x≤2时,y随x的增大而增大,求a的取值范围.
(3)若函数图象与x轴无交点,求a2+b2的取值范围.
【分析】(1)把点A(﹣1,1)和B(2,4)代入解析式得到,两式相减即可得到结论;
(2)由题意可知1,代入b=1﹣a,解得a,即可得到a的取值范围是0<a;
(3)由b=1﹣a得到a2+b2=2(a)2,即可根据二次函数的性质得到a2+b2的最值.
【解答】解:(1)∵二次函数y=ax2+bx+c(a>0)的图象经过点A(﹣1,1)和B(2,4),
∴,
②﹣①得,3a+3b=3,即a+b=1,
∴b=1﹣a;
(2)由题意可知1,
∵b=1﹣a,
∴1,
∴a>0,
∴1﹣a≥2a,
∴a,
∴a的取值范围是0<a;
(3)∵函数图象与x轴无交点,
∴b2﹣4ac<0,即(1﹣a)2﹣4a(2﹣2a)<0,
∴(1﹣a)(1﹣9a)<0,
解得a<1,
∵b=1﹣a,
∴a2+b2
=a2+(1﹣a)2
=a2+a2﹣2a+1
=2a2﹣2a+1
=2(a)2,
∴当a时,a2+b2的最小值为,
当a=1时,a2+b2的最大值为1,
∴a2+b2<1.
44.(2022秋 滨江区期末)二次函数y=x2﹣bx+c的图象经过(﹣2,y1),(1,y2)两点.
(1)当b=1时,判断y1与y2的大小.
(2)当y1<y2时,求b的取值范围.
(3)若此函数图象还经过点(m,y1),且1<b<2,求证:3<m<4.
【分析】(1)当b=1时,分别把x=﹣2,x=1代入解析式,计算出y1,y2,比较即可;
(2)先求出y1=4+2b+c,y2=1﹣b+c,再根据y1<y2,解不等式即可;
(3)先求出二次函数y=x2﹣bx+c的对称轴为直线x,m得由1<b<2,计算可得答案.
【解答】解:(1)当b=1时,
∴,
∵6+c>c,
∴y1>y2;
(2)∵y1=4+2b+c,y2=1﹣b+c,
又∵y1<y2,
∴4+2b+c<1﹣b+c,
∴b<﹣1;
(3)二次函数y=x2﹣bx+c的对称轴为直线,
∵二次函数经过(﹣2,y1),(m,y1)两点,
∴m得,即m=2+b,
∵1<b<2,
∴3<m<4.
45.(2023秋 杭州期末)综合与实践:问题情境:求方程x2+x﹣1=0的解,就是求二次函数y=x2+x﹣1的图象与x轴交点的横坐标.为了估计这个方程的解,圆圆先取了6个自变量满足x1<x2<x3<x4<x5<x6且x1﹣x2=x2﹣x3=x3﹣x4=x4﹣x5=x5﹣x6,再分别算出相应的y值.列表得:
x的值 x1 x2 x3 x4 x5 x6
y=x2+x﹣1的值 1 0.71 0.44 0.19 0.04 ﹣0.25
操作判断:(1)求x1的值;
实践探究:(2)为了分析函数值的变化规律,圆圆将表格中得到的函数值逐个作差.如:0.71﹣1=﹣0.29,0.44﹣0.71=﹣0.27,得到如下数据:﹣0.29,﹣0.27,﹣0.25,﹣0.15,﹣0.29,通过计算,圆圆发现自己由于粗心算错了其中的一个函数值,请指出算错的是哪一个值,正确的是多少?
问题解决:(3)对于一般的二次函数y=ax2+bx+c(a≠0,a、b、c为常数)的函数值变化进行如表研究:(d≠0)
x的值 x x+d x+2d x+3d x+4d x+5d
y=ax2+bx+c的值 y1 y2 y3 y4 y5 y6
将表格中得到的函数值逐个作差,发现函数值的差与自变量满足某种函数关系,请写出你的发现过程以及发现结论.
【分析】(1)把y=1代入y=x2+x﹣1,求得相应的x的值,根据函数值的变化选取合适的x的值;
(2)作差后的前三个数据分别是前一个数据的基础上增加0.02,第四个不是,所以猜测第五个函数值错了,设出第五个函数值为m,根据第五个函数值减去第四个函数值的值为﹣0.25+0.02列式计算即可;
(3)可设函数值的差为w,若自变量为x,那么和它相邻的自变量为x+d,分别求得它们的函数值,相减即可得到w.
【解答】解:(1)把y=1代入y=x2+x﹣1,得:
x2+x﹣1=1,
解得x1=﹣2,x2=1.
∵二次函数y=x2+x﹣1的对称轴为直线x,
∴当x时,y随着x的增大而减小.观察图表可得y随x的增大而减小.
∴.
∴x1=﹣2.
(2)作差后的前三个数据﹣0.29,﹣0.27,﹣0.25分别是前一个数的基础上增加0.02,第四个不是.
∴猜测第五个函数值错了.
设第5个函数值为m.
∴m﹣0.19=﹣0.25+0.02.
解得:m=﹣0.04.
答:第五个函数值错了,应该是﹣0.04.
(3)设函数值的差为w,
猜测:函数值的差与自变量满足一次函数关系,
若自变量为x,则函数值为:yn=ax2+bx+c;
和x相邻的自变量为x+d,则函数值为:yn+1=a(x+d)2+b(x+d)+c.
∴w=[a(x+d)2+b(x+d)+c]﹣(ax2+bx+c)
=2adx+(ad2+bd).
∵a,b,c,d为常数,且a≠0,d≠0,
∴函数值的差与自变量满足一次函数关系.w=2adx+(ad2+bd)(a≠0,d≠0,a、b、c、d为常数).
46.(2023秋 杭州期末)已知二次函数y=ax2﹣2ax+1(a≠0),图象经过点(﹣1,m),(1,n),(3,p).
(1)当m=﹣2时.
①求二次函数的表达式;
②写出一个符合条件的x的取值范围,使得y随x的增大而增大;
(2)若在m,n,p这三个实数中,只有一个是正数,求证:.
【分析】(1)①利用待定系数法即可解决问题.
②根据所得二次函数的图象和性质即可解决问题.
(2)由这三个点在抛物线上的位置即可解决问题.
【解答】解:(1)①当m=﹣2时,
将点(﹣1,﹣2)代入函数解析式得,
a+2a+1=﹣2,
解得a=﹣1.
所以二次函数的表达式为y=﹣x2+2x+1.
②因为抛物线的对称轴为直线x,且开口向下,
所以当x<1时,y随x的增大而增大.
故一个符合条件的x的取值范围是:x<1.
证明:(2)因为抛物线的对称轴为直线x,
又因为1﹣(﹣1)=3﹣1,
所以点(﹣1,m)和点(3,p)关于抛物线的对称轴对称,
则m=p.
又因为m,n,p这三个实数中,只有一个是正数,
所以m和p都是非正数,n是正数,
则,
解得.
所以a.
47.(2023秋 拱墅区校级期末)已知二次函数y=x2﹣4x﹣5,点P1(x1,y1)与P2(x2,y2)都在该函数的图象上,且x1+x2=2.
(1)求函数图象的顶点;
(2)若点P1(x1,y1)与P2(x2,y2)与直线x=m的距离恒相等,求m的值;
(3)若y1≥y2,求y1的最小值.
【分析】(1)把解析式化成顶点式即可求解;
(2)根据题意,列出方程,化简后将x1+x2=2代入即可求解;
(3)根据题意,由(1)(2)可得,P1在直线x=1的左侧,P2在直线x=1的右侧或重合在直线x=1上,根据二次函数的增减性即可求解.
【解答】解(1)∵二次函数y=x2﹣4x﹣5=(x﹣2)2﹣9,
∴函数图象的顶点为(2,﹣9).
(2)∵点P1(x1,y1)与P2(x2,y2)与直线x=m的距离恒相等,
∴|x1﹣m|=|x2﹣m|,
∴(x1﹣m)2=(x2﹣m)2,
化简得(x1﹣x2)[(x1+x2)﹣2m]=0,
又∵x1+x2=2,x1≠x2,
∴m=1.
故m的值为1.
(3)∵y1≥y2,
由(1)(2)可得,P1在直线x=1的左侧,P2在直线x=1的右侧或重合在直线x=1上,
∴x1≤1,
∵y1随x1的增大而减小,
∴当x1=1时,y1的最小值为﹣8.
故y1≥y2时,y1的最小值为﹣8.
48.(2023秋 滨江区期末)【综合与实践】
【认识研究对象】教材121页给出了如下定义:如图1,如果点P把线段AB分成两条线段AP和PB(AP>PB),且,则我们称点P为线段AB的黄金分割点.类似,我们可以定义:如果一个三角形中,其最长边的长度和最短边的长度的乘积等于第三边长度的平方,那么就称该三角形为“类黄金三角形”.
如图2,已知△ABC是“类黄金三角形”,且AC<AB<BC.若AC=3,BC=5,求AB的长.
【探索研究方法】如图3,已知△ABC是“类黄金三角形”,且AC<AB<BC.
若∠BAC=90°,小滨同学过点A作AD⊥BC于点D,发现了两个结论:
①AB2=BD×BC;
②点D是边BC的黄金分割点;
请给出证明.
【尝试问题解决】小滨同学经历以上探索过程发现:类似问题,可以通过构造相似三角形等方法解决.于是开展新的探
同课章节目录
