24.1.3弧、弦、圆心角 教学设计(表格式)2024-2025学年人教版数学九年级上册
文档属性
| 名称 | 24.1.3弧、弦、圆心角 教学设计(表格式)2024-2025学年人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 242.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-14 21:39:56 | ||
图片预览

文档简介
弧、弦、圆心角课时教学设计
课题 24.1.3弧、弦、圆心角
课型 新授课 复习课□ 试卷讲评课□ 其它课□
教学内容分析: 本节课是通过白板动画演示学生观察、思考、交流合作活动,教师演示动态课件及引导,让学生感受圆的对称性,研究圆中的圆心角、弧、弦间的关系定理。
学情分析: 这一节的内容实际还是属于旋转对称的,围绕圆心旋转任意角度,都能与原来的图形重合。这节课就是根据圆的旋转不变性,推出了弦、弧、圆心角之间的关系,初三的孩子逻辑能力较强,但对于圆的认识比较浅显,故在掌握知识的同时注意教学方式的灵活性和深度。
学习目标: 知道圆心角的定义,能利用圆的旋转对称性证明弧、弦、圆心角之间的关系,并会用几何符号表示. 能利用弧、弦、圆心角之间的关系证明角相等、线段相等、弧相等.
重难点: 知道圆心角的定义,能利用圆的旋转对称性证明弧、弦、圆心角之间的关系,并会用几何符号表示. 能利用弧、弦、圆心角之间的关系证明角相等、线段相等、弧相等.
评价任务: 达成目标1的标志:能在几何图形中识别出圆心角, 并能用符号语言推出弧、弦、圆心角之间的关系定理. 达成目标2的标志:利用弧、弦、圆心角之间的关系定理,证明角相等、线段相等、弧相等.
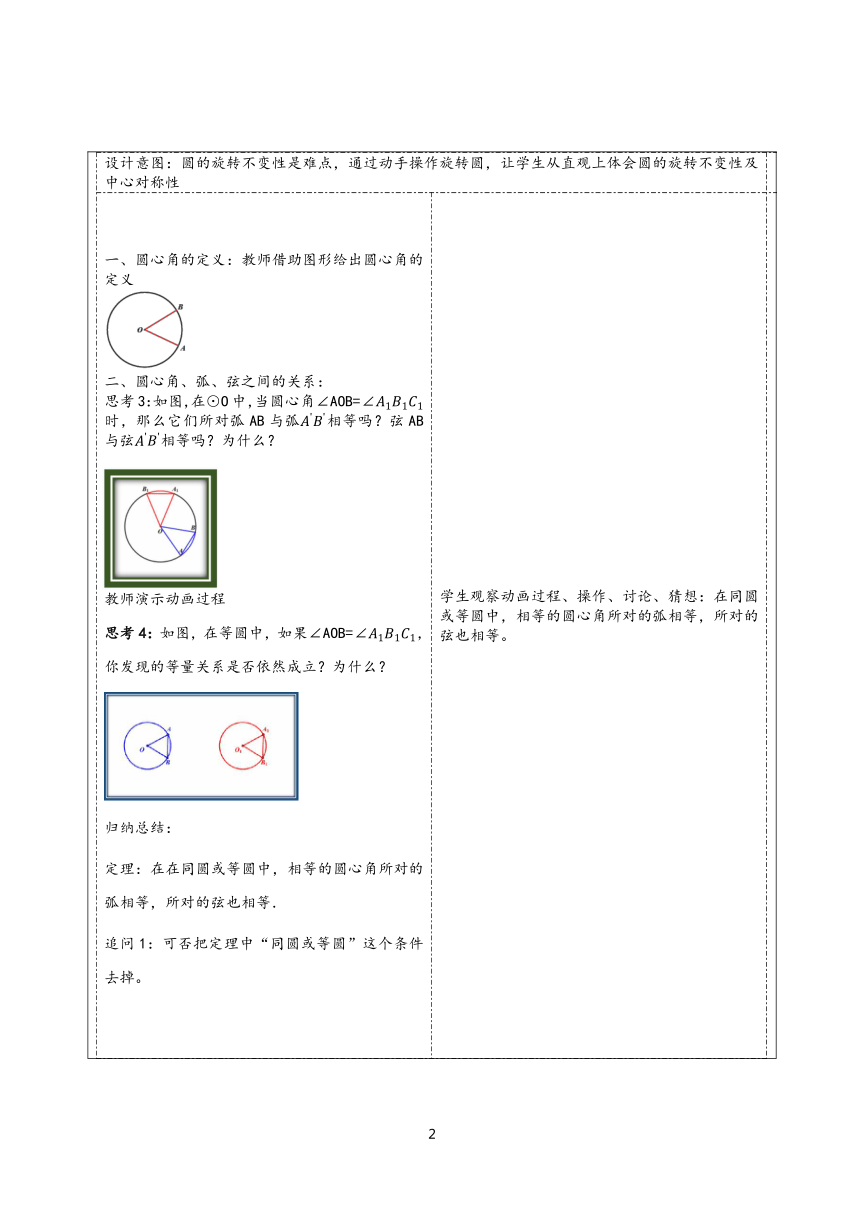
教学评活动过程 教师活动学生活动环节一:复习引入问题一:圆是轴对称图形吗?圆对称轴是什么? 问题二:垂径定理的内容是什么? 问题三:什么是中心对称图形?学生思考后回答设计意图:通过对圆的轴对称性,对比学习圆的旋转不变性,从整体上更清晰地认识圆。环节二:新知探究思考1:将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢? 思考2:把圆绕圆心旋转任意一个角度后,还能和原来的图形重合吗? 教师进行演示 学生观察动画演示过程,作出回答,同时归纳: 圆是中心对称图形,对称中心是圆心。 圆具有旋转不变性设计意图:圆的旋转不变性是难点,通过动手操作旋转圆,让学生从直观上体会圆的旋转不变性及中心对称性 圆心角的定义:教师借助图形给出圆心角的定义 圆心角、弧、弦之间的关系: 思考3:如图,在⊙O中,当圆心角∠AOB=∠时,那么它们所对弧AB与弧相等吗?弦AB与弦相等吗?为什么? 教师演示动画过程 思考4:如图,在等圆中,如果∠AOB=∠,你发现的等量关系是否依然成立?为什么? 归纳总结: 定理:在在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等. 追问1:可否把定理中“同圆或等圆”这个条件去掉。 追问2:在同圆或等圆中,如果两条弧相等,你能发现哪些等量关系?为什么? 追问3:在同圆或等圆中,如果两条弦相等,你能发现哪些等量关系?为什么? 学生观察动画过程、操作、讨论、猜想:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。 学生观察、讨论后回答:不能 学生类比定理的探究方法研究圆心角、弧、弦这三组量中,只要有一组量相等,那么其余的各组量也相等。 设计意图:让学生感受类比思想,类比中全面透彻地理解和掌握关系定理和它的推论,并进行推广,得到其他几个定理,完整的把握所学知识,给出一般叙述,以其更好的应用.环节三:概念巩固问题:如图,AB、CD是⊙O的两条弦 如果AB=CD,那么 如果弧AB=弧CD,那么 如果∠AOB= ∠COD,那么 学生独立思考并回答设计意图:培养学生的概括总结能力,更直观地帮助学生理解概念环节四:典例解析1、例:如图,在⊙O中,,∠ACB=60°,求证:∠AOB=∠AOC=∠BOC. (老师引导学生一起分析并写出推理过程) 练习 如图,AB是⊙O的直径,弧BC=弧CD=弧DE,∠COD=40°,求∠AOE的度数. 学生独立完成,指名板演设计意图:通过例题和练习,带同学们熟悉定理和推论以及规范地答题过程环节五:课堂小结 圆是中心对称图形,圆具有旋转不变性; 定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等. 环节六:作业布置 1、已知:如图所示,在⊙O中,AD=BC,比较AB与CD的长度,并证明你的结论, 2、如图,AB,CD是⊙O的两条弦,OE⊥AB于E,OF⊥CD于F. 如果AB=CD, OE与OF相等吗?为什么?
板书设计 《弧、弦、圆心角》 学生演板: 复习引入 例题1:解: (评价纠错,强调规范书写) 二、圆心角、弧、弦之间的关系及推论
课题 24.1.3弧、弦、圆心角
课型 新授课 复习课□ 试卷讲评课□ 其它课□
教学内容分析: 本节课是通过白板动画演示学生观察、思考、交流合作活动,教师演示动态课件及引导,让学生感受圆的对称性,研究圆中的圆心角、弧、弦间的关系定理。
学情分析: 这一节的内容实际还是属于旋转对称的,围绕圆心旋转任意角度,都能与原来的图形重合。这节课就是根据圆的旋转不变性,推出了弦、弧、圆心角之间的关系,初三的孩子逻辑能力较强,但对于圆的认识比较浅显,故在掌握知识的同时注意教学方式的灵活性和深度。
学习目标: 知道圆心角的定义,能利用圆的旋转对称性证明弧、弦、圆心角之间的关系,并会用几何符号表示. 能利用弧、弦、圆心角之间的关系证明角相等、线段相等、弧相等.
重难点: 知道圆心角的定义,能利用圆的旋转对称性证明弧、弦、圆心角之间的关系,并会用几何符号表示. 能利用弧、弦、圆心角之间的关系证明角相等、线段相等、弧相等.
评价任务: 达成目标1的标志:能在几何图形中识别出圆心角, 并能用符号语言推出弧、弦、圆心角之间的关系定理. 达成目标2的标志:利用弧、弦、圆心角之间的关系定理,证明角相等、线段相等、弧相等.
教学评活动过程 教师活动学生活动环节一:复习引入问题一:圆是轴对称图形吗?圆对称轴是什么? 问题二:垂径定理的内容是什么? 问题三:什么是中心对称图形?学生思考后回答设计意图:通过对圆的轴对称性,对比学习圆的旋转不变性,从整体上更清晰地认识圆。环节二:新知探究思考1:将圆绕圆心旋转180°后,得到的图形与原图形重合吗?由此你得到什么结论呢? 思考2:把圆绕圆心旋转任意一个角度后,还能和原来的图形重合吗? 教师进行演示 学生观察动画演示过程,作出回答,同时归纳: 圆是中心对称图形,对称中心是圆心。 圆具有旋转不变性设计意图:圆的旋转不变性是难点,通过动手操作旋转圆,让学生从直观上体会圆的旋转不变性及中心对称性 圆心角的定义:教师借助图形给出圆心角的定义 圆心角、弧、弦之间的关系: 思考3:如图,在⊙O中,当圆心角∠AOB=∠时,那么它们所对弧AB与弧相等吗?弦AB与弦相等吗?为什么? 教师演示动画过程 思考4:如图,在等圆中,如果∠AOB=∠,你发现的等量关系是否依然成立?为什么? 归纳总结: 定理:在在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等. 追问1:可否把定理中“同圆或等圆”这个条件去掉。 追问2:在同圆或等圆中,如果两条弧相等,你能发现哪些等量关系?为什么? 追问3:在同圆或等圆中,如果两条弦相等,你能发现哪些等量关系?为什么? 学生观察动画过程、操作、讨论、猜想:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。 学生观察、讨论后回答:不能 学生类比定理的探究方法研究圆心角、弧、弦这三组量中,只要有一组量相等,那么其余的各组量也相等。 设计意图:让学生感受类比思想,类比中全面透彻地理解和掌握关系定理和它的推论,并进行推广,得到其他几个定理,完整的把握所学知识,给出一般叙述,以其更好的应用.环节三:概念巩固问题:如图,AB、CD是⊙O的两条弦 如果AB=CD,那么 如果弧AB=弧CD,那么 如果∠AOB= ∠COD,那么 学生独立思考并回答设计意图:培养学生的概括总结能力,更直观地帮助学生理解概念环节四:典例解析1、例:如图,在⊙O中,,∠ACB=60°,求证:∠AOB=∠AOC=∠BOC. (老师引导学生一起分析并写出推理过程) 练习 如图,AB是⊙O的直径,弧BC=弧CD=弧DE,∠COD=40°,求∠AOE的度数. 学生独立完成,指名板演设计意图:通过例题和练习,带同学们熟悉定理和推论以及规范地答题过程环节五:课堂小结 圆是中心对称图形,圆具有旋转不变性; 定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等. 环节六:作业布置 1、已知:如图所示,在⊙O中,AD=BC,比较AB与CD的长度,并证明你的结论, 2、如图,AB,CD是⊙O的两条弦,OE⊥AB于E,OF⊥CD于F. 如果AB=CD, OE与OF相等吗?为什么?
板书设计 《弧、弦、圆心角》 学生演板: 复习引入 例题1:解: (评价纠错,强调规范书写) 二、圆心角、弧、弦之间的关系及推论
同课章节目录
