第二章 二次函数 小结与复习课件(共30张PPT ) 2024-2025学年北师大版九年级数学下册
文档属性
| 名称 | 第二章 二次函数 小结与复习课件(共30张PPT ) 2024-2025学年北师大版九年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 4.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-14 21:31:44 | ||
图片预览










文档简介
(共30张PPT)
小结与复习
第二章 二次函数
一、二次函数的定义
1.一般地,如果 y=ax2+bx+c(a,b,c是常数,a≠0),那么 y 叫做 x 的二次函数.特别地,当 a≠0,b=c=0 时,
y=ax2 是二次函数的特殊形式.
2.二次函数的三种基本形式
(1)一般式:y=ax2+bx+c(a,b,c是常数,a≠0);
(2)顶点式:y=a(x-h)2+k(a≠0),由顶点式可以直接写出二次函数的顶点坐标是(h,k);
(3)交点式:y=a(x-x1)(x-x2)(a≠0),其中 x1,x2 是图象与 x 轴交点的横坐标.
二、二次函数的图象和性质
二次函数 y = a(x h)2 + k y = ax2 + bx + c
开口 方向 对称轴
顶点坐标
最值 a>0
a<0
增减性 a>0 a<0 a>0 时开口向上
a<0 时开口向下
x = h
(h,k)
y最小 = k
y最大 = k
在对称轴左边 x↗y↗,在对称轴右边 x↗y↘
在对称轴左边 x↗y↘,在对称轴右边 x↗y↗
y最小=
y最大=
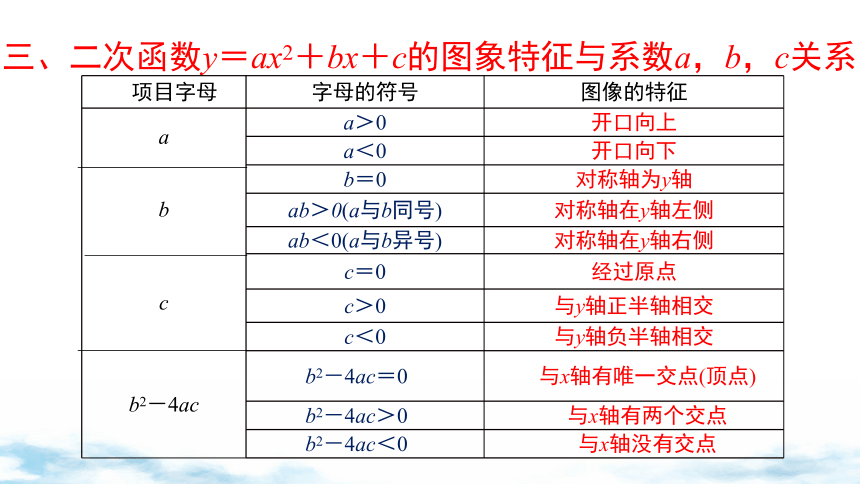
三、二次函数y=ax2+bx+c的图象特征与系数a,b,c关系
项目字母 字母的符号 图像的特征
a a>0 开口向上
a<0 开口向下
b b=0 对称轴为y轴
ab>0(a与b同号) 对称轴在y轴左侧
ab<0(a与b异号) 对称轴在y轴右侧
c c=0 经过原点
c>0 与y轴正半轴相交
c<0 与y轴负半轴相交
b2-4ac b2-4ac=0 与x轴有唯一交点(顶点)
b2-4ac>0 与x轴有两个交点
b2-4ac<0 与x轴没有交点
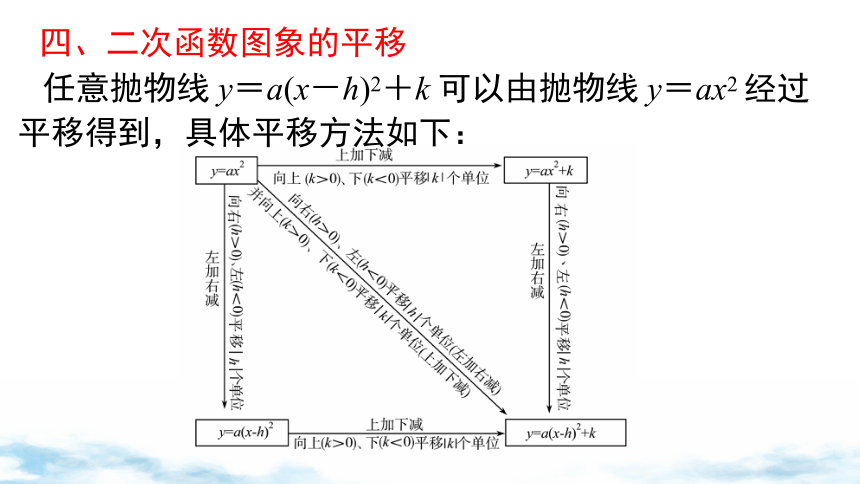
四、二次函数图象的平移
任意抛物线 y=a(x-h)2+k 可以由抛物线 y=ax2 经过平移得到,具体平移方法如下:
五、二次函数表达式的求法
1.一般式:y=ax2+bx+c (a≠0)
若已知条件是图象上三个点的坐标,则设一般式 y=ax2+bx+c(a≠0),将已知条件代入,求出 a,b,c 的值.
2.顶点式:y=a(x-h)2+k (a≠0)
若已知二次函数的顶点坐标或对称轴方程与最大值或最小值,则设顶点式 y=a(x-h)2+k(a≠0),将已知条件代入,求出待定系数的值,最后将表达式化为一般式.
3.交点式:y=a(x-x1)(x-x2)(a≠0)
若已知二次函数图象与 x 轴的两个交点的坐标,则设交点式 y=a(x-x1)(x-x2)(a≠0),将第三点的坐标或其他已知条件代入,求出待定系数 a 的值,最后将表达式化为一般式.
六、二次函数与一元二次方程的关系
二次函数 y=ax2+bx+c 的图象和 x 轴交点有三种情况:有两个交点,有一个交点,没有交点.当二次函数 y=ax2+bx+c 的图象和 x 轴有交点时,交点的横坐标就是当 y=0 时自变量 x 的值,即一元二次方程 ax2+bx+c=0 的根.
二次函数 y=ax2+bx+c 的图象和 x 轴交点 一元二次方程 ax2+bx+c=0 的根 一元二次方程
ax2+bx+c=0根的判别式(b2-4ac)
有两个交点
有两个相异的实数根
b2-4ac > 0
有一个交点
有两个相等的实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
七、二次函数的应用
2.一般步骤:(1)找出问题中的变量和常量以及它们之间的函数关系;(2)列出函数关系式,并确定自变量的取值范围;(3)利用二次函数的图象及性质解决实际问题;(4)检验结果的合理性,是否符合实际意义.
1.二次函数的应用包括以下两个方面
(1)用二次函数表示实际问题变量之间的关系,解决最大化问题(即最值问题);
(2)利用二次函数的图象求一元二次方程的近似根及一元二次不等式的解集.
方法二:
代入公式 , ,则顶点坐标为 (1,2).
考点一 求抛物线的顶点、对称轴、最值
例1 抛物线 y=x2-2x+3 的顶点坐标为______.
【解析】方法一:
配方,得 y=x2-2x+3=(x-1)2+2,则顶点坐标为(1,2).
(1,2)
1.对于 y=2(x-3)2+2 的图象下列叙述正确的是( )
A.顶点坐标为(-3,2)
B.对称轴为 y=3
C.当 x≥3 时,y 随 x 的增大而增大
D.当 x=3 时,y 取最大值,为2
C
针对训练
考点二 二次函数的增减性
例2 二次函数 y=-x2+bx+c 的图象如图所示,若点 A(x1,y1),B(x2,y2)在此函数图象上,且 x1 < x2 < 1,则 y1 与 y2 的大小关系是( )
A. y1≤y2 B.y1 < y2
C.y1≥y2 D.y1 > y2
【解析】由图象看出,抛物线开口向下,对称轴是直线 x=1,当 x<1 时,y 随 x 的增大而增大.
∵x1< x2 < 1,∴y1 < y2 . 故选B.
B
当二次函数的表达式与已知点的坐标中含有未知字母时,可以用如下方法比较函数值的大小:
(1)用含有未知字母的代数式表示各函数值,然后进行比较;
(2)在相应的范围内取未知字母的特殊值,采用特殊值法求解;
(3)根据二次函数的性质,结合函数图象比较.
方法总结
2.下列函数中,当 x>0 时,y 值随 x 值增大而减小的是( )
A. y = x2 B. y = x - 1
C. D. y = -3x2
D
针对训练
例3 如图是二次函数 y=ax2+bx+c(a≠0) 图象的一部分,
x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c= -9a;④若(-3,y1),( ,y2)是抛物线上两点,则 y1>y2.其中正确的是 ( )
A.①②③
B.①③④
C.①②④
D.②③④
x
y
O
2
x=-1
B
考点三 二次函数的图象与系数的关系
3.已知二次函数 y=-x2+2bx+c,当 x>1 时,y 的值随 x 值的增大而减小,则实数 b 的取值范围( )
A.b≥-1 B.b≤-1
C.b≥1 D.b≤1
解析:∵二次项系数为-1<0,
∴由题设可知,当 x>1 时,y 的值随 x 值的增大而减小,∴抛物线 y=-x2+2bx+c 的对称轴应在直线 x=1 的左侧而抛物线 y=-x2+2bx+c 的对称轴 ,b≤1,故选择 D.
D
针对训练
考点四 抛物线的平移变换
例4 将抛物线 y=x2-6x+5 向上平移 2 个单位长度,再向右平移 1 个单位长度后,得到的抛物线表达式是( )
A.y=(x-4)2-6 B.y=(x-4)2-2
C.y=(x-2)2-2 D.y=(x-1)2-3
【解析】因为 y=x2-6x+5=(x-3)2-4,所以向上平移 2 个单位长度,再向右平移 1 个单位长度后,得到的表达式为 y=(x-3-1)2-4+2,即 y=(x-4)2-2.故选 B.
B
4. 若抛物线 y = -7(x + 4)2-1 平移得到 y = -7x2,则必须( )
A. 先向左平移 4 个单位,再向上平移 1 个单位
B. 先向右平移 4 个单位,再向上平移 1 个单位
C. 先向左平移 1 个单位,再向下平移 4 个单位
D. 先向右平移 1 个单位,再向下平移 4 个单位
B
针对训练
考点五 二次函数表达式的确定
例5 已知关于 x 的二次函数,当 x = -1 时,函数值为 10,当 x = 1 时,函数值为 4,当 x = 2 时,函数值为 7,求这个二次函数的表达式.
待定系数法
解:设所求的二次函数为 y=ax2+bx+c,由题意得:
解得, a = 2,b = -3,c = 5.
∴ 所求的二次函数表达式为 y=2x2-3x+5.
5.已知抛物线 y = ax2 + bx + c 与抛物线 y = -x2-3x+7的形状相同,顶点在直线 x = 1 上,且顶点到 x 轴的距离为 5,请写出满足此条件的抛物线的表达式.
解:∵抛物线 y = ax2 + bx + c 与抛物线 y = -x2-3x + 7 的形状相同,∴ a = 1或-1.
针对训练
∴其表达式为:
(1) y = (x-1)2+5 (2) y = (x-1)2-5
(3) y = -(x-1)2+5 (4) y = -(x-1)2-5
又∵顶点在直线 x = 1 上,且顶点到 x 轴的距离为 5,
∴ 顶点为(1,5)或(1,-5).
例6 若二次函数 y = x2 + mx 的对称轴是 x = 3,则关于 x 的方程 x2 + mx = 7 的解为( )
A.x1 = 0,x2 = 6 B.x1 = 1,x2 = 7
C.x1 = 1,x2 =﹣7 D.x1 =﹣1,x2 = 7
【解答】∵二次函数 y = x2 + mx 的对称轴是 x = 3,
∴- =3,解得 m=-6,
考点六 二次函数与一元二次方程
D
故选 D.
∴关于 x 的方程 x2 + mx = 7 可化为 x2-6x-7=0,
即(x + 1)(x - 7) = 0,解得 x1 =-1,x2 = 7.
例7 如图,梯形 ABCD 中,AB∥DC,∠ABC=90°,∠A=45°,AB=30,BC=x,其中15<x<30.作DE⊥AB 于点 E,将 △ADE 沿直线 DE 折叠,点 A 落在 F 处,DF 交 BC 于点 G.
(1) 用含有 x 的代数式表示 BF 的长;
(2) 设四边形 DEBG 的面积为 S,求 S 与 x 的函数关系式;(3) 当 x 为何值时,S 有最大值?
并求出这个最大值.
考点七 二次函数的应用
解:(1) 由题意,得 EF = AE = DE = BC = x, AB = 30.
∴ BF = 2x - 30.
(2) ∵∠F =∠A = 45°,∠CBF = ∠ABC = 90°,
∴∠BGF = ∠F = 45°,BG = BF = 2x - 30.
∴ S△DEF - S△GBF = DE2 - BF2 = x2 - (2x - 30)2
= x2 + 60x - 450.
(3)S = x2 + 60x - 450 = (x - 20)2 + 150.
∵a = <0,15<20<30,
∴当 x = 20 时,S 有最大值.
最大值为 150.
6. 某商场试销一种成本为每件 60 元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于 45%,经试销发现,销售量 y (件)与销售单价 x (元)符合一次函数 y=kx+b,且 x=65 时,y=55;x=75 时,y=45.
(1) 求一次函数的表达式;
(2) 若该商场获得利润为W 元,试写出利润W 与销售单价 x 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
解:(1) 根据题意,得
解得 k=-1,b=120.故所求一次函数的表达式为 y=-x+120.
(2)W=(x - 60) (-x + 120)=-x2+180x-7200=-(x-90)2+900,
∵抛物线的开口向下,
∴当 x<90 时,W 随 x 的增大而增大.
而 60≤x≤60×(1+45%),即 60≤x≤87,
∴当 x=87 时,W 有最大值,此时 W=-(87- 90)2+900=891.
考点八 二次函数与几何的综合
例8 如图,在平面直角坐标系中,点 A 在抛物线
y = x2 - 2x + 3 上运动.过点 A 作 AC⊥x 轴于点 C,以 AC 为对角线作矩形 ABCD,连接 BD,则对角线 BD 的最小值为( )
A.1 B.2
C.3 D.4
B
7. 如图,抛物线 y = x2 + bx + c 经过点(1,-4)和(-2,5),请解答下列问题:
(1)求抛物线的表达式;
解:(1)由题意,得
所以,该抛物线的表达式为 y = x2 - 2x - 3;
解得
(2)∵抛物线 y = x2 - 2x - 3 的对称轴为 x = 1,
∴图中点 C 关于 x = 1 的对称点 D 即为所求,
(2)若抛物线与 x 轴的两个交点为 A、B,与 y 轴交于点C.在该抛物线上是否存在点 D,使得 △ABC 与 △ABD 全等?若存在,求出 D 点的坐标;若不存在,请说明理由.
在 y = x2 - 2x - 3 中,令 x = 0,得 y = -3,
则 C(0,-3),∴D(2,-3).
∴△ABC≌△BAD(SSS).
在 △ABC 和 △BAD 中,
此时,AC = BD,BC = AD,
二次函数
图象画法
抛物线的开口方向
抛物线的顶点坐标和对称轴
二次函数的性质
抛物线的平移
最值
确定
表达式
应用
见教材章末练习
小结与复习
第二章 二次函数
一、二次函数的定义
1.一般地,如果 y=ax2+bx+c(a,b,c是常数,a≠0),那么 y 叫做 x 的二次函数.特别地,当 a≠0,b=c=0 时,
y=ax2 是二次函数的特殊形式.
2.二次函数的三种基本形式
(1)一般式:y=ax2+bx+c(a,b,c是常数,a≠0);
(2)顶点式:y=a(x-h)2+k(a≠0),由顶点式可以直接写出二次函数的顶点坐标是(h,k);
(3)交点式:y=a(x-x1)(x-x2)(a≠0),其中 x1,x2 是图象与 x 轴交点的横坐标.
二、二次函数的图象和性质
二次函数 y = a(x h)2 + k y = ax2 + bx + c
开口 方向 对称轴
顶点坐标
最值 a>0
a<0
增减性 a>0 a<0 a>0 时开口向上
a<0 时开口向下
x = h
(h,k)
y最小 = k
y最大 = k
在对称轴左边 x↗y↗,在对称轴右边 x↗y↘
在对称轴左边 x↗y↘,在对称轴右边 x↗y↗
y最小=
y最大=
三、二次函数y=ax2+bx+c的图象特征与系数a,b,c关系
项目字母 字母的符号 图像的特征
a a>0 开口向上
a<0 开口向下
b b=0 对称轴为y轴
ab>0(a与b同号) 对称轴在y轴左侧
ab<0(a与b异号) 对称轴在y轴右侧
c c=0 经过原点
c>0 与y轴正半轴相交
c<0 与y轴负半轴相交
b2-4ac b2-4ac=0 与x轴有唯一交点(顶点)
b2-4ac>0 与x轴有两个交点
b2-4ac<0 与x轴没有交点
四、二次函数图象的平移
任意抛物线 y=a(x-h)2+k 可以由抛物线 y=ax2 经过平移得到,具体平移方法如下:
五、二次函数表达式的求法
1.一般式:y=ax2+bx+c (a≠0)
若已知条件是图象上三个点的坐标,则设一般式 y=ax2+bx+c(a≠0),将已知条件代入,求出 a,b,c 的值.
2.顶点式:y=a(x-h)2+k (a≠0)
若已知二次函数的顶点坐标或对称轴方程与最大值或最小值,则设顶点式 y=a(x-h)2+k(a≠0),将已知条件代入,求出待定系数的值,最后将表达式化为一般式.
3.交点式:y=a(x-x1)(x-x2)(a≠0)
若已知二次函数图象与 x 轴的两个交点的坐标,则设交点式 y=a(x-x1)(x-x2)(a≠0),将第三点的坐标或其他已知条件代入,求出待定系数 a 的值,最后将表达式化为一般式.
六、二次函数与一元二次方程的关系
二次函数 y=ax2+bx+c 的图象和 x 轴交点有三种情况:有两个交点,有一个交点,没有交点.当二次函数 y=ax2+bx+c 的图象和 x 轴有交点时,交点的横坐标就是当 y=0 时自变量 x 的值,即一元二次方程 ax2+bx+c=0 的根.
二次函数 y=ax2+bx+c 的图象和 x 轴交点 一元二次方程 ax2+bx+c=0 的根 一元二次方程
ax2+bx+c=0根的判别式(b2-4ac)
有两个交点
有两个相异的实数根
b2-4ac > 0
有一个交点
有两个相等的实数根
b2-4ac = 0
没有交点
没有实数根
b2-4ac < 0
七、二次函数的应用
2.一般步骤:(1)找出问题中的变量和常量以及它们之间的函数关系;(2)列出函数关系式,并确定自变量的取值范围;(3)利用二次函数的图象及性质解决实际问题;(4)检验结果的合理性,是否符合实际意义.
1.二次函数的应用包括以下两个方面
(1)用二次函数表示实际问题变量之间的关系,解决最大化问题(即最值问题);
(2)利用二次函数的图象求一元二次方程的近似根及一元二次不等式的解集.
方法二:
代入公式 , ,则顶点坐标为 (1,2).
考点一 求抛物线的顶点、对称轴、最值
例1 抛物线 y=x2-2x+3 的顶点坐标为______.
【解析】方法一:
配方,得 y=x2-2x+3=(x-1)2+2,则顶点坐标为(1,2).
(1,2)
1.对于 y=2(x-3)2+2 的图象下列叙述正确的是( )
A.顶点坐标为(-3,2)
B.对称轴为 y=3
C.当 x≥3 时,y 随 x 的增大而增大
D.当 x=3 时,y 取最大值,为2
C
针对训练
考点二 二次函数的增减性
例2 二次函数 y=-x2+bx+c 的图象如图所示,若点 A(x1,y1),B(x2,y2)在此函数图象上,且 x1 < x2 < 1,则 y1 与 y2 的大小关系是( )
A. y1≤y2 B.y1 < y2
C.y1≥y2 D.y1 > y2
【解析】由图象看出,抛物线开口向下,对称轴是直线 x=1,当 x<1 时,y 随 x 的增大而增大.
∵x1< x2 < 1,∴y1 < y2 . 故选B.
B
当二次函数的表达式与已知点的坐标中含有未知字母时,可以用如下方法比较函数值的大小:
(1)用含有未知字母的代数式表示各函数值,然后进行比较;
(2)在相应的范围内取未知字母的特殊值,采用特殊值法求解;
(3)根据二次函数的性质,结合函数图象比较.
方法总结
2.下列函数中,当 x>0 时,y 值随 x 值增大而减小的是( )
A. y = x2 B. y = x - 1
C. D. y = -3x2
D
针对训练
例3 如图是二次函数 y=ax2+bx+c(a≠0) 图象的一部分,
x=-1是对称轴,有下列判断:①b-2a=0;②4a-2b+c<0;③a-b+c= -9a;④若(-3,y1),( ,y2)是抛物线上两点,则 y1>y2.其中正确的是 ( )
A.①②③
B.①③④
C.①②④
D.②③④
x
y
O
2
x=-1
B
考点三 二次函数的图象与系数的关系
3.已知二次函数 y=-x2+2bx+c,当 x>1 时,y 的值随 x 值的增大而减小,则实数 b 的取值范围( )
A.b≥-1 B.b≤-1
C.b≥1 D.b≤1
解析:∵二次项系数为-1<0,
∴由题设可知,当 x>1 时,y 的值随 x 值的增大而减小,∴抛物线 y=-x2+2bx+c 的对称轴应在直线 x=1 的左侧而抛物线 y=-x2+2bx+c 的对称轴 ,b≤1,故选择 D.
D
针对训练
考点四 抛物线的平移变换
例4 将抛物线 y=x2-6x+5 向上平移 2 个单位长度,再向右平移 1 个单位长度后,得到的抛物线表达式是( )
A.y=(x-4)2-6 B.y=(x-4)2-2
C.y=(x-2)2-2 D.y=(x-1)2-3
【解析】因为 y=x2-6x+5=(x-3)2-4,所以向上平移 2 个单位长度,再向右平移 1 个单位长度后,得到的表达式为 y=(x-3-1)2-4+2,即 y=(x-4)2-2.故选 B.
B
4. 若抛物线 y = -7(x + 4)2-1 平移得到 y = -7x2,则必须( )
A. 先向左平移 4 个单位,再向上平移 1 个单位
B. 先向右平移 4 个单位,再向上平移 1 个单位
C. 先向左平移 1 个单位,再向下平移 4 个单位
D. 先向右平移 1 个单位,再向下平移 4 个单位
B
针对训练
考点五 二次函数表达式的确定
例5 已知关于 x 的二次函数,当 x = -1 时,函数值为 10,当 x = 1 时,函数值为 4,当 x = 2 时,函数值为 7,求这个二次函数的表达式.
待定系数法
解:设所求的二次函数为 y=ax2+bx+c,由题意得:
解得, a = 2,b = -3,c = 5.
∴ 所求的二次函数表达式为 y=2x2-3x+5.
5.已知抛物线 y = ax2 + bx + c 与抛物线 y = -x2-3x+7的形状相同,顶点在直线 x = 1 上,且顶点到 x 轴的距离为 5,请写出满足此条件的抛物线的表达式.
解:∵抛物线 y = ax2 + bx + c 与抛物线 y = -x2-3x + 7 的形状相同,∴ a = 1或-1.
针对训练
∴其表达式为:
(1) y = (x-1)2+5 (2) y = (x-1)2-5
(3) y = -(x-1)2+5 (4) y = -(x-1)2-5
又∵顶点在直线 x = 1 上,且顶点到 x 轴的距离为 5,
∴ 顶点为(1,5)或(1,-5).
例6 若二次函数 y = x2 + mx 的对称轴是 x = 3,则关于 x 的方程 x2 + mx = 7 的解为( )
A.x1 = 0,x2 = 6 B.x1 = 1,x2 = 7
C.x1 = 1,x2 =﹣7 D.x1 =﹣1,x2 = 7
【解答】∵二次函数 y = x2 + mx 的对称轴是 x = 3,
∴- =3,解得 m=-6,
考点六 二次函数与一元二次方程
D
故选 D.
∴关于 x 的方程 x2 + mx = 7 可化为 x2-6x-7=0,
即(x + 1)(x - 7) = 0,解得 x1 =-1,x2 = 7.
例7 如图,梯形 ABCD 中,AB∥DC,∠ABC=90°,∠A=45°,AB=30,BC=x,其中15<x<30.作DE⊥AB 于点 E,将 △ADE 沿直线 DE 折叠,点 A 落在 F 处,DF 交 BC 于点 G.
(1) 用含有 x 的代数式表示 BF 的长;
(2) 设四边形 DEBG 的面积为 S,求 S 与 x 的函数关系式;(3) 当 x 为何值时,S 有最大值?
并求出这个最大值.
考点七 二次函数的应用
解:(1) 由题意,得 EF = AE = DE = BC = x, AB = 30.
∴ BF = 2x - 30.
(2) ∵∠F =∠A = 45°,∠CBF = ∠ABC = 90°,
∴∠BGF = ∠F = 45°,BG = BF = 2x - 30.
∴ S△DEF - S△GBF = DE2 - BF2 = x2 - (2x - 30)2
= x2 + 60x - 450.
(3)S = x2 + 60x - 450 = (x - 20)2 + 150.
∵a = <0,15<20<30,
∴当 x = 20 时,S 有最大值.
最大值为 150.
6. 某商场试销一种成本为每件 60 元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于 45%,经试销发现,销售量 y (件)与销售单价 x (元)符合一次函数 y=kx+b,且 x=65 时,y=55;x=75 时,y=45.
(1) 求一次函数的表达式;
(2) 若该商场获得利润为W 元,试写出利润W 与销售单价 x 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
解:(1) 根据题意,得
解得 k=-1,b=120.故所求一次函数的表达式为 y=-x+120.
(2)W=(x - 60) (-x + 120)=-x2+180x-7200=-(x-90)2+900,
∵抛物线的开口向下,
∴当 x<90 时,W 随 x 的增大而增大.
而 60≤x≤60×(1+45%),即 60≤x≤87,
∴当 x=87 时,W 有最大值,此时 W=-(87- 90)2+900=891.
考点八 二次函数与几何的综合
例8 如图,在平面直角坐标系中,点 A 在抛物线
y = x2 - 2x + 3 上运动.过点 A 作 AC⊥x 轴于点 C,以 AC 为对角线作矩形 ABCD,连接 BD,则对角线 BD 的最小值为( )
A.1 B.2
C.3 D.4
B
7. 如图,抛物线 y = x2 + bx + c 经过点(1,-4)和(-2,5),请解答下列问题:
(1)求抛物线的表达式;
解:(1)由题意,得
所以,该抛物线的表达式为 y = x2 - 2x - 3;
解得
(2)∵抛物线 y = x2 - 2x - 3 的对称轴为 x = 1,
∴图中点 C 关于 x = 1 的对称点 D 即为所求,
(2)若抛物线与 x 轴的两个交点为 A、B,与 y 轴交于点C.在该抛物线上是否存在点 D,使得 △ABC 与 △ABD 全等?若存在,求出 D 点的坐标;若不存在,请说明理由.
在 y = x2 - 2x - 3 中,令 x = 0,得 y = -3,
则 C(0,-3),∴D(2,-3).
∴△ABC≌△BAD(SSS).
在 △ABC 和 △BAD 中,
此时,AC = BD,BC = AD,
二次函数
图象画法
抛物线的开口方向
抛物线的顶点坐标和对称轴
二次函数的性质
抛物线的平移
最值
确定
表达式
应用
见教材章末练习
