北师版数学七年级下册第二章相交线与平行线专题练习
文档属性
| 名称 | 北师版数学七年级下册第二章相交线与平行线专题练习 |  | |
| 格式 | zip | ||
| 文件大小 | 185.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-03 09:09:39 | ||
图片预览


文档简介
北师版数学七年级下册第二章专题练习
一.解答题(共29小题)
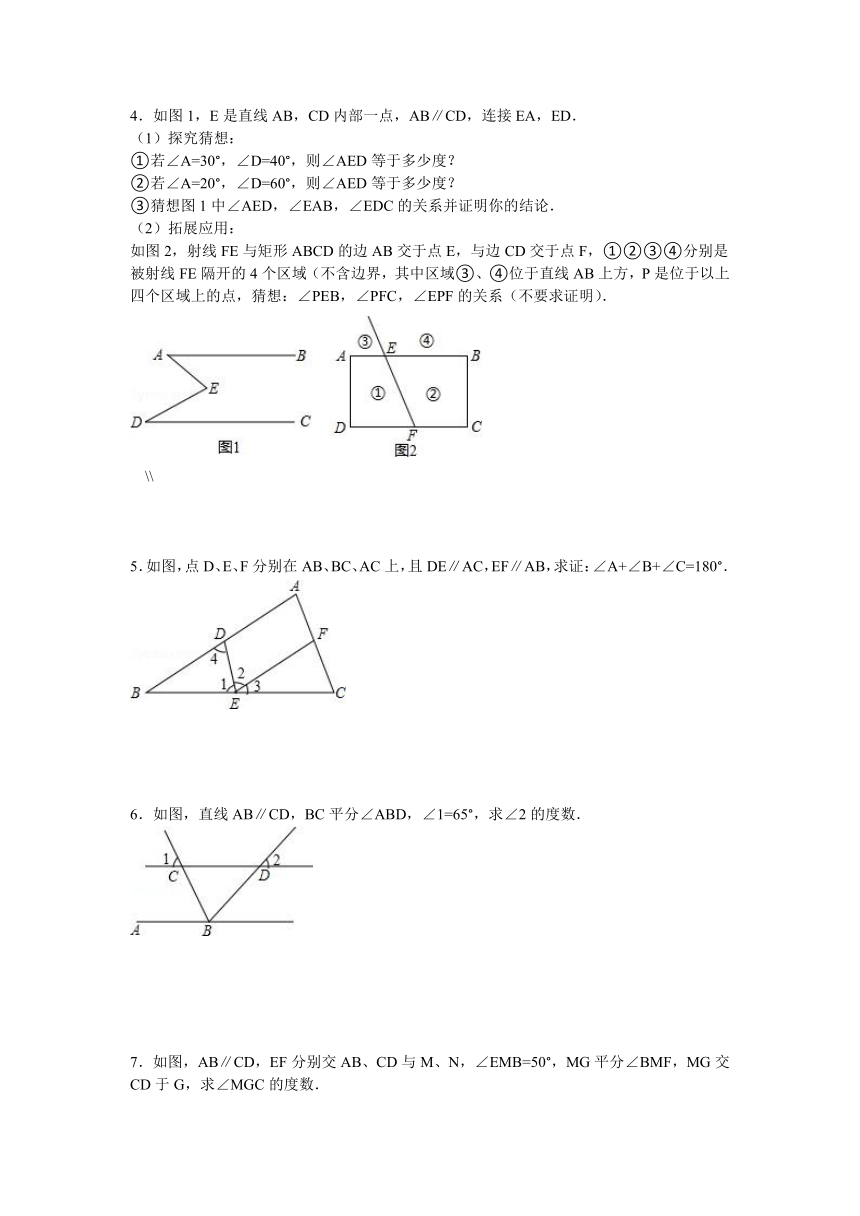
1.如图,AB∥ED,∠B=48°,∠D=42°,BC垂直于CD吗?下面给出两种添加辅助线的方法,请选择一种,对你作出的结论加以说明.
( http: / / www.21cnjy.com )
2.如图,已知直线l1∥l2,直线l3和 ( http: / / www.21cnjy.com )直线l1、l2交于点C和D,在C、D之间有一点P,如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化.若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
( http: / / www.21cnjy.com )
3.如图1,AB∥CD,EOF是直线AB、CD间的一条折线.
(1)试证明:∠O=∠BEO+∠DFO.
(2)如果将折一次改为折二次,如图2,则∠BEO、∠O、∠P、∠PFC之间会满足怎样的数量关系,证明你的结论.
( http: / / www.21cnjy.com )
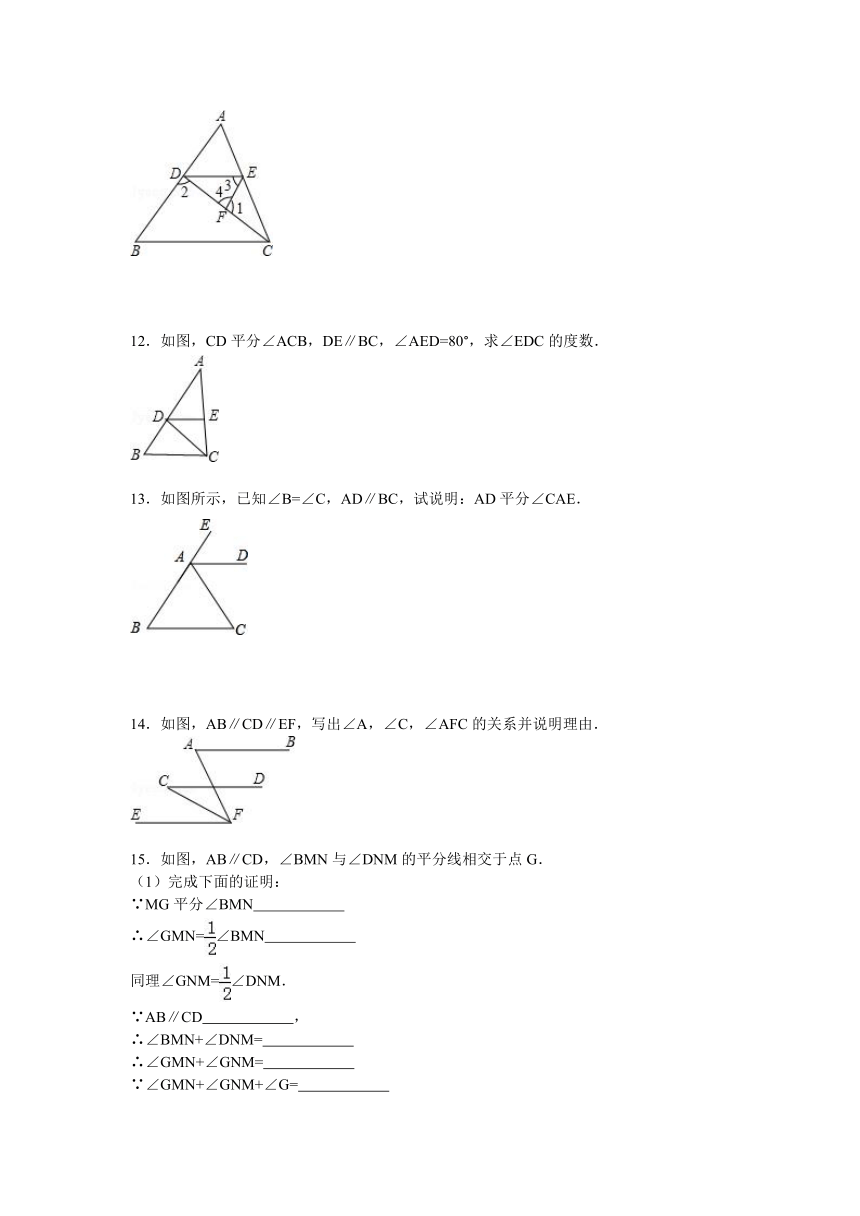
4.如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③猜想图1中∠AED,∠EAB,∠EDC的关系并证明你的结论.
(2)拓展应用:
如图2,射线FE与矩形ABCD的边AB交于 ( http: / / www.21cnjy.com )点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区域③、④位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(不要求证明).
( http: / / www.21cnjy.com )
\\
5.如图,点D、E、F分别在AB、BC、AC上,且DE∥AC,EF∥AB,求证:∠A+∠B+∠C=180°.
( http: / / www.21cnjy.com )
6.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
( http: / / www.21cnjy.com )
7.如图,AB∥CD,EF分别交AB、CD与M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠MGC的度数.
( http: / / www.21cnjy.com )
8.已知:如图,在四边形ABCD中,∠A=130°,∠C=90°,∠D=40°,BE∥AD交CD于点E.求证:BE平分∠ABC.
( http: / / www.21cnjy.com )
9.如图:AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2等于多少度?
( http: / / www.21cnjy.com )
10.如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD.
( http: / / www.21cnjy.com )
11.如图,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并说明理由.
( http: / / www.21cnjy.com )
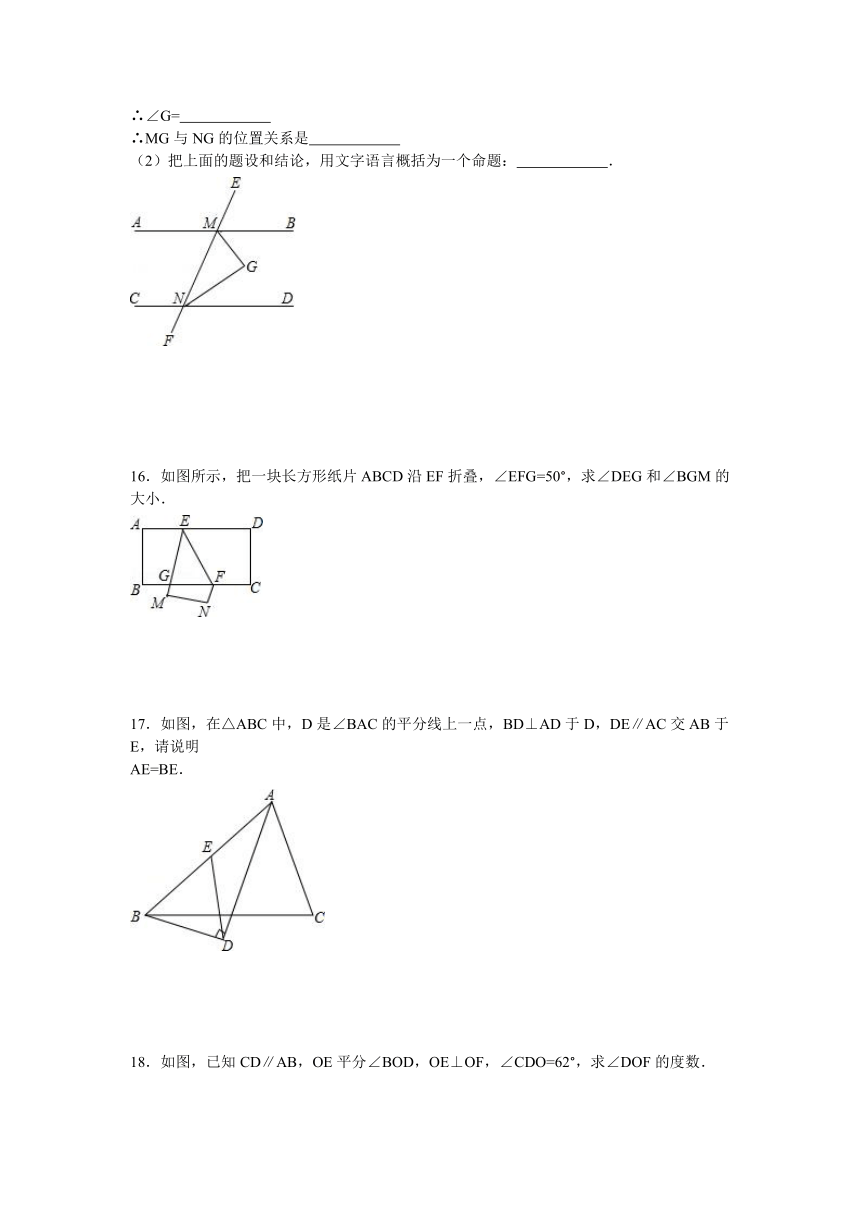
12.如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.
( http: / / www.21cnjy.com )
13.如图所示,已知∠B=∠C,AD∥BC,试说明:AD平分∠CAE.
( http: / / www.21cnjy.com )
14.如图,AB∥CD∥EF,写出∠A,∠C,∠AFC的关系并说明理由.
( http: / / www.21cnjy.com )
15.如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G.
(1)完成下面的证明:
∵MG平分∠BMN
∴∠GMN=∠BMN
同理∠GNM=∠DNM.
∵AB∥CD ,
∴∠BMN+∠DNM=
∴∠GMN+∠GNM=
∵∠GMN+∠GNM+∠G=
∴∠G=
∴MG与NG的位置关系是
(2)把上面的题设和结论,用文字语言概括为一个命题: .
( http: / / www.21cnjy.com )
16.如图所示,把一块长方形纸片ABCD沿EF折叠,∠EFG=50°,求∠DEG和∠BGM的大小.
( http: / / www.21cnjy.com )
17.如图,在△ABC中,D是∠BAC的平分线上一点,BD⊥AD于D,DE∥AC交AB于E,请说明
AE=BE.
( http: / / www.21cnjy.com )
18.如图,已知CD∥AB,OE平分∠BOD,OE⊥OF,∠CDO=62°,求∠DOF的度数.
( http: / / www.21cnjy.com )
\\
19.如图,AB∥EF∥CD,∠ABC=45°,∠CEF=155°,求∠BCE的度数.
( http: / / www.21cnjy.com )
20.(2015春 霸州市期末)已知:如图,AB∥EF,BC∥ED,AB,DE交于点G.
求证:∠B=∠E.
( http: / / www.21cnjy.com )
21.如图,AB∥CD,直线EF分别交AB、CD于E、F两点,∠BEF的平分线交CD于点G,若∠EFG=72°,求∠EGF的度数.
( http: / / www.21cnjy.com )
22.如图所示,直线a∥b,AC丄AB,AC交直线b于点C,∠1=60°,求∠2的度数.
( http: / / www.21cnjy.com )
23.已知:如图,AB∥CD,MN截AB、CD于E、F,且EG∥FH,求证:∠1=∠2.
( http: / / www.21cnjy.com )
24.如图,直线AB,CD相交于点O,OE⊥AB,OF⊥CD.
(1)若OC恰好是∠AOE的平分线,则OA是∠COF的平分线吗?请说明理由;
(2)若∠EOF=5∠BOD,求∠COE的度数.
( http: / / www.21cnjy.com )
25.如图,己知∠A=∠1,∠C=∠F,请问BC与EF平行吗?请说明理由.
( http: / / www.21cnjy.com )
26.已知:如图,AB⊥BC,BC⊥CD且∠1=∠2,求证:BE∥CF.
( http: / / www.21cnjy.com )
27.如图,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F.试说明:EC∥DF.
( http: / / www.21cnjy.com )
28.已知:如图,BE平分∠ABC,∠1=∠2.那么BC与DE平行吗?请说明理由.
( http: / / www.21cnjy.com )
29.如图,直线a∥b,点B在直线上b上,且AB⊥BC,∠1=55°,求∠2的度数.
( http: / / www.21cnjy.com )
参考答案
一.解答题(共29小题)
1.解:过点C作CF∥AB,
∵AB∥ED,
∴AB∥CF∥ED,
∴∠BCF=∠B,∠DCF=∠D,
∴∠BCD=∠B+∠D,
=48°+42°,
=90°,
∴BC⊥CD;
过点C作CG∥AB,
∵AB∥ED,
∴AB∥CG∥ED,
∴∠BCG=180°﹣∠B=180°﹣48°=132°,
∠DCG=∠D=180°﹣∠D=180°﹣42°=138°,
∴∠BCD=360°﹣∠BCG﹣∠DCG,
=360°﹣132°﹣138°,
=90°,
∴BC⊥CD.
2.解:如图①,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
如图②,当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:
∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
如图③,当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
理由如下:
∵l1∥l2,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
( http: / / www.21cnjy.com )
3.(1)证明:作OM∥AB,如图1,
∴∠1=∠BEO,
∵AB∥CD,
∴OM∥CD,
∴∠2=∠DFO,
∴∠1+∠2=∠BEO+∠DFO,
即:∠O=∠BEO+∠DFO.
(2)解:∠O+∠PFC=∠BEO+∠P.理由如下:
作OM∥AB,PN∥CD,如图2,
∵AB∥CD,
∴OM∥PN∥AB∥CD,
∴∠1=∠BEO,∠2=∠3,∠4=∠PFC,
∴∠1+∠2+∠PFC=∠BEO+∠3+∠4,
∴∠O+∠PFC=∠BEO+∠P.
( http: / / www.21cnjy.com )
4.解:(1)①∠AED=70°;
②∠AED=80°;
③猜想:∠AED=∠EAB+∠EDC,
证明:延长AE交DC于点F,
∵AB∥DC,
∴∠EAB=∠EFD,
∵∠AED为△EDF的外角,
∴∠AED=∠EDF+∠EFD=∠EAB+∠EDC;
(2)根据题意得:
点P在区域①时,∠EPF=360°﹣(∠PEB+∠PFC);
点P在区域②时,∠EPF=∠PEB+∠PFC;
点P在区域③时,∠EPF=∠PEB﹣∠PFC;
点P在区域④时,∠EPF=∠PFC﹣∠PEB.
( http: / / www.21cnjy.com )
5.证明:∵DE∥AC,
∴∠1=∠C,∠A=∠4,
∵EF∥AB,
∴∠3=∠B,∠4=∠2,
∴∠2=∠A,
∵∠1+∠2+∠3=180°,
∴∠A+∠B+∠C=180°.
6.解:∵AB∥CD,
∴∠ABC=∠1=65°,∠ABD+∠BDC=180°,
∵BC平分∠ABD,
∴∠ABD=2∠ABC=130°,
∴∠BDC=180°﹣∠ABD=50°,
∴∠2=∠BDC=50°.
7.解:∵∠EMB=50°,
∴∠BMF=180°﹣50°=130°.
∵MG平分∠BMF,
∴∠BMG=∠BMF=65°.
∵AB∥CD,
∴∠MGC=∠BMG=65°.
8.证明:∵在四边形ABCD中,∠A=130°,∠C=90°,∠D=40°,
∴∠ABC=360°﹣130°﹣90°﹣40°=100°.
∵BE∥AD,
∴∠ABE=180°﹣∠A=180°﹣130°=50°,
∴∠ABE=∠ABC,即BE平分∠ABC.
9.解:∵AB∥CD,∠1=72°,
∴∠BEF=180°﹣∠1=180°﹣72°=108°,∠2=∠BEG,
∵EG平分∠BEF,
∴∠BEG=∠BEF=×108°=54°,即∠2=54°.
10.解:∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等);
∵∠1=∠2(已知),
∴∠1=∠3(等量代换);
∴DG∥AB(内错角相等,两直线平行).
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).
∵∠BAC=70°,
∴∠AGD=110°.
( http: / / www.21cnjy.com )
11.解:∠AED=∠ACB.
理由:∵∠1+∠4=180°(平角定义),∠1+∠2=180°(已知).
∴∠2=∠4.
∴EF∥AB(内错角相等,两直线平行).
∴∠3=∠ADE(两直线平行,内错角相等).
∵∠3=∠B(已知),
∴∠B=∠ADE(等量代换).
∴DE∥BC(同位角相等,两直线平行).
∴∠AED=∠ACB(两直线平行,同位角相等).
12.解:∵DE∥BC,∠AED=80°,
∴∠ACB=∠AED=80°(两直线平行,同位角相等),
∵CD平分∠ACB,
∴∠BCD=∠ACB=40°,
∵DE∥BC,
∴∠EDC=∠BCD=40°(两直线平行,内错角相等).
13.证明:∵AD∥BC(已知)
∴∠B=∠EAD(两直线平行,同位角相等)
∠DAC=∠C(两直线平行,内错角相等)
又∵∠B=∠C(已知)
∴∠EAD=∠DAC(等量代换)
∴AD平分∠CAE(角平分线的定义).
14.解:∠A=∠C+∠AFC.理由如下:
如图,
∵AB∥CD,
∴∠A=∠1,
∵∠1=∠C+∠AFC,
∴∠A=∠C+∠AFC.
( http: / / www.21cnjy.com )
15.解:∵MG平分∠BMN(已知)
∴∠GMN=∠BMN(角平分线的定义),
同理∠GNM=∠DNM.
∵AB∥CD(已知),
∴∠BMN+∠DNM=180°,
∴∠GMN+∠GNM=90°,
∵∠GMN+∠GNM+∠G=180°,
∴∠G=90°,
∴MG与NG的位置关系是MG⊥NG;
故答案为:已知;角平分线的定义;已知;180°;90°;180°;90°;MG⊥NG;
(2)两平行直线被第三条直线所截,同旁内角的角平分线互相垂直.
16.解:∵AD∥BC,∠EFG=50°,
∴∠EFC=180°﹣∠EFG=130°,
由折叠的性质可知,∠NFE=∠EFC,∠MEF=∠DEF,
∴∠DEG=100°,
∴∠EGC=180°﹣100°=80°,
则∠BGM=∠EGC=80°(对顶角相等).
17.证明:∵DE∥AC,
∴∠ADE=∠CAD,
∵AD是∠BAC的平分线,
∴∠EAD=∠CAD,
∴∠ADE=∠EAD,
∴AE=DE,
∵BD⊥AD,
∴∠ADE+∠BDE=90°,∠EAD+∠ABD=90°,
∴∠ABD=∠BDE,
∴BE=DE,
∴AE=BE.
18.解:∵CD∥AB,
∴∠BOD=180°﹣∠CDO=180°﹣62°=128°,
∵OE平分∠BOD,
∴∠DOE=∠BOD=×118°=59°,
∵OE⊥OF,
∴∠EOF=90°,
∴∠DOF=∠EOF﹣∠DOE=90°﹣59°=31°.
19.解:∵AB∥CD,
∴∠ABC=∠BCD=45°,
∵EF∥CD,
∴∠FEC+∠ECD=180°,
∵∠CEF=155°,
∴∠ECD=25°,
∴∠BCE=∠BCD﹣∠ECD=20°.
20.证明:∵AB∥EF,
∴∠E=∠AGD,
∵BC∥ED,
∴∠B=∠AGD,
∴∠B=∠E.
21.解:∵AB∥CD,∠EFG=72°(已知)
∴∠BEF=108°(两直线平行,同旁内角互补)
∵EG平分∠BEF,
∴∠BEG=54°(角平分线定义)
∴∠EGF=∠BEG=54°(两直线平行,内错角相等).
22.解:∵AC丄AB,
∴∠BAC=90°,
∵∠1=60°,
∴∠B=180°﹣∠1﹣∠BAC=30°,
∵a∥b,
∴∠2=∠B=30°.
23.证明:∵AB∥CD,
∴∠MEB=∠MFD,
∵EG∥FH,
∴∠MEG=∠MFH,
∴∠MEB﹣∠MEG=∠MFD﹣∠MFH,
即∠1=∠2.
24.解:(1)OA是∠COF的平分线.
∵OE⊥AB,
∴∠AOE=90°,
∵OC恰好是∠AOE的平分线,
∴∠AOC==45°,
∵OF⊥CD,
∴∠COF=90°,
∴∠AOF=∠COF﹣∠AOC=90°﹣45°=45°,
∴OA是∠COF的平分线;
(2)设∠AOC=x,
∴∠BOD=x,
∵∠AOE=90°,
∴∠COE=∠AOE﹣∠AOC=90°﹣x,
∴∠EOF=∠COE+∠COF=90°﹣x+90°=180°﹣x,
∵∠EOF=5∠BOD,
∴180°﹣x=5x,
解得x=30,
∴∠COE=90°﹣30°=60°.
25.解:BC∥EF.
∵△ACB和△DFE中,∠A=∠1,∠C=∠F,
∴∠B=∠E.
∴BC∥EF.
26.证明:∵AB⊥BC,BC⊥CD,
∴∠ABC=∠DCB=90°,
∵∠1=∠2,
∴∠ABC﹣∠1=∠DCB﹣∠2,
∴∠CBE=∠BCF,
∴BE∥CF.
27.解:∵BD平分∠ABC,CE平分∠ACB,
∴∠DBF=∠ABC,∠ECB=∠ACB,
∵∠ABC=∠ACB,
∴∠DBF=∠ECB,
∵∠DBF=∠F,
∴∠ECB=∠F,
∴EC∥DF.
28.解:BC∥DE,
理由如下:
∵BE平分∠ABC,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3,
∴BC∥DE.
29.解: ( http: / / www.21cnjy.com )
∵AB⊥BC,
∴∠ABC=90°,
∴∠1+∠3=90°,
∵∠1=55°,
∴∠3=35°,
∵a∥b,
∴∠2=∠3=35°.
一.解答题(共29小题)
1.如图,AB∥ED,∠B=48°,∠D=42°,BC垂直于CD吗?下面给出两种添加辅助线的方法,请选择一种,对你作出的结论加以说明.
( http: / / www.21cnjy.com )
2.如图,已知直线l1∥l2,直线l3和 ( http: / / www.21cnjy.com )直线l1、l2交于点C和D,在C、D之间有一点P,如果P点在C、D之间运动时,问∠PAC,∠APB,∠PBD之间的关系是否发生变化.若点P在C、D两点的外侧运动时(P点与点C、D不重合),试探索∠PAC,∠APB,∠PBD之间的关系又是如何?
( http: / / www.21cnjy.com )
3.如图1,AB∥CD,EOF是直线AB、CD间的一条折线.
(1)试证明:∠O=∠BEO+∠DFO.
(2)如果将折一次改为折二次,如图2,则∠BEO、∠O、∠P、∠PFC之间会满足怎样的数量关系,证明你的结论.
( http: / / www.21cnjy.com )
4.如图1,E是直线AB,CD内部一点,AB∥CD,连接EA,ED.
(1)探究猜想:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③猜想图1中∠AED,∠EAB,∠EDC的关系并证明你的结论.
(2)拓展应用:
如图2,射线FE与矩形ABCD的边AB交于 ( http: / / www.21cnjy.com )点E,与边CD交于点F,①②③④分别是被射线FE隔开的4个区域(不含边界,其中区域③、④位于直线AB上方,P是位于以上四个区域上的点,猜想:∠PEB,∠PFC,∠EPF的关系(不要求证明).
( http: / / www.21cnjy.com )
\\
5.如图,点D、E、F分别在AB、BC、AC上,且DE∥AC,EF∥AB,求证:∠A+∠B+∠C=180°.
( http: / / www.21cnjy.com )
6.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
( http: / / www.21cnjy.com )
7.如图,AB∥CD,EF分别交AB、CD与M、N,∠EMB=50°,MG平分∠BMF,MG交CD于G,求∠MGC的度数.
( http: / / www.21cnjy.com )
8.已知:如图,在四边形ABCD中,∠A=130°,∠C=90°,∠D=40°,BE∥AD交CD于点E.求证:BE平分∠ABC.
( http: / / www.21cnjy.com )
9.如图:AB∥CD,直线EF分别交AB、CD于E、F,EG平分∠BEF,若∠1=72°,则∠2等于多少度?
( http: / / www.21cnjy.com )
10.如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD.
( http: / / www.21cnjy.com )
11.如图,已知∠1+∠2=180°,∠3=∠B,试判断∠AED与∠ACB的大小关系,并说明理由.
( http: / / www.21cnjy.com )
12.如图,CD平分∠ACB,DE∥BC,∠AED=80°,求∠EDC的度数.
( http: / / www.21cnjy.com )
13.如图所示,已知∠B=∠C,AD∥BC,试说明:AD平分∠CAE.
( http: / / www.21cnjy.com )
14.如图,AB∥CD∥EF,写出∠A,∠C,∠AFC的关系并说明理由.
( http: / / www.21cnjy.com )
15.如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G.
(1)完成下面的证明:
∵MG平分∠BMN
∴∠GMN=∠BMN
同理∠GNM=∠DNM.
∵AB∥CD ,
∴∠BMN+∠DNM=
∴∠GMN+∠GNM=
∵∠GMN+∠GNM+∠G=
∴∠G=
∴MG与NG的位置关系是
(2)把上面的题设和结论,用文字语言概括为一个命题: .
( http: / / www.21cnjy.com )
16.如图所示,把一块长方形纸片ABCD沿EF折叠,∠EFG=50°,求∠DEG和∠BGM的大小.
( http: / / www.21cnjy.com )
17.如图,在△ABC中,D是∠BAC的平分线上一点,BD⊥AD于D,DE∥AC交AB于E,请说明
AE=BE.
( http: / / www.21cnjy.com )
18.如图,已知CD∥AB,OE平分∠BOD,OE⊥OF,∠CDO=62°,求∠DOF的度数.
( http: / / www.21cnjy.com )
\\
19.如图,AB∥EF∥CD,∠ABC=45°,∠CEF=155°,求∠BCE的度数.
( http: / / www.21cnjy.com )
20.(2015春 霸州市期末)已知:如图,AB∥EF,BC∥ED,AB,DE交于点G.
求证:∠B=∠E.
( http: / / www.21cnjy.com )
21.如图,AB∥CD,直线EF分别交AB、CD于E、F两点,∠BEF的平分线交CD于点G,若∠EFG=72°,求∠EGF的度数.
( http: / / www.21cnjy.com )
22.如图所示,直线a∥b,AC丄AB,AC交直线b于点C,∠1=60°,求∠2的度数.
( http: / / www.21cnjy.com )
23.已知:如图,AB∥CD,MN截AB、CD于E、F,且EG∥FH,求证:∠1=∠2.
( http: / / www.21cnjy.com )
24.如图,直线AB,CD相交于点O,OE⊥AB,OF⊥CD.
(1)若OC恰好是∠AOE的平分线,则OA是∠COF的平分线吗?请说明理由;
(2)若∠EOF=5∠BOD,求∠COE的度数.
( http: / / www.21cnjy.com )
25.如图,己知∠A=∠1,∠C=∠F,请问BC与EF平行吗?请说明理由.
( http: / / www.21cnjy.com )
26.已知:如图,AB⊥BC,BC⊥CD且∠1=∠2,求证:BE∥CF.
( http: / / www.21cnjy.com )
27.如图,∠ABC=∠ACB,BD平分∠ABC,CE平分∠ACB,∠DBF=∠F.试说明:EC∥DF.
( http: / / www.21cnjy.com )
28.已知:如图,BE平分∠ABC,∠1=∠2.那么BC与DE平行吗?请说明理由.
( http: / / www.21cnjy.com )
29.如图,直线a∥b,点B在直线上b上,且AB⊥BC,∠1=55°,求∠2的度数.
( http: / / www.21cnjy.com )
参考答案
一.解答题(共29小题)
1.解:过点C作CF∥AB,
∵AB∥ED,
∴AB∥CF∥ED,
∴∠BCF=∠B,∠DCF=∠D,
∴∠BCD=∠B+∠D,
=48°+42°,
=90°,
∴BC⊥CD;
过点C作CG∥AB,
∵AB∥ED,
∴AB∥CG∥ED,
∴∠BCG=180°﹣∠B=180°﹣48°=132°,
∠DCG=∠D=180°﹣∠D=180°﹣42°=138°,
∴∠BCD=360°﹣∠BCG﹣∠DCG,
=360°﹣132°﹣138°,
=90°,
∴BC⊥CD.
2.解:如图①,当P点在C、D之间运动时,∠APB=∠PAC+∠PBD.
理由如下:
过点P作PE∥l1,
∵l1∥l2,
∴PE∥l2∥l1,
∴∠PAC=∠1,∠PBD=∠2,
∴∠APB=∠1+∠2=∠PAC+∠PBD;
如图②,当点P在C、D两点的外侧运动,且在l1上方时,∠PBD=∠PAC+∠APB.
理由如下:
∵l1∥l2,
∴∠PEC=∠PBD,
∵∠PEC=∠PAC+∠APB,
∴∠PBD=∠PAC+∠APB.
如图③,当点P在C、D两点的外侧运动,且在l2下方时,∠PAC=∠PBD+∠APB.
理由如下:
∵l1∥l2,
∴∠PED=∠PAC,
∵∠PED=∠PBD+∠APB,
∴∠PAC=∠PBD+∠APB.
( http: / / www.21cnjy.com )
3.(1)证明:作OM∥AB,如图1,
∴∠1=∠BEO,
∵AB∥CD,
∴OM∥CD,
∴∠2=∠DFO,
∴∠1+∠2=∠BEO+∠DFO,
即:∠O=∠BEO+∠DFO.
(2)解:∠O+∠PFC=∠BEO+∠P.理由如下:
作OM∥AB,PN∥CD,如图2,
∵AB∥CD,
∴OM∥PN∥AB∥CD,
∴∠1=∠BEO,∠2=∠3,∠4=∠PFC,
∴∠1+∠2+∠PFC=∠BEO+∠3+∠4,
∴∠O+∠PFC=∠BEO+∠P.
( http: / / www.21cnjy.com )
4.解:(1)①∠AED=70°;
②∠AED=80°;
③猜想:∠AED=∠EAB+∠EDC,
证明:延长AE交DC于点F,
∵AB∥DC,
∴∠EAB=∠EFD,
∵∠AED为△EDF的外角,
∴∠AED=∠EDF+∠EFD=∠EAB+∠EDC;
(2)根据题意得:
点P在区域①时,∠EPF=360°﹣(∠PEB+∠PFC);
点P在区域②时,∠EPF=∠PEB+∠PFC;
点P在区域③时,∠EPF=∠PEB﹣∠PFC;
点P在区域④时,∠EPF=∠PFC﹣∠PEB.
( http: / / www.21cnjy.com )
5.证明:∵DE∥AC,
∴∠1=∠C,∠A=∠4,
∵EF∥AB,
∴∠3=∠B,∠4=∠2,
∴∠2=∠A,
∵∠1+∠2+∠3=180°,
∴∠A+∠B+∠C=180°.
6.解:∵AB∥CD,
∴∠ABC=∠1=65°,∠ABD+∠BDC=180°,
∵BC平分∠ABD,
∴∠ABD=2∠ABC=130°,
∴∠BDC=180°﹣∠ABD=50°,
∴∠2=∠BDC=50°.
7.解:∵∠EMB=50°,
∴∠BMF=180°﹣50°=130°.
∵MG平分∠BMF,
∴∠BMG=∠BMF=65°.
∵AB∥CD,
∴∠MGC=∠BMG=65°.
8.证明:∵在四边形ABCD中,∠A=130°,∠C=90°,∠D=40°,
∴∠ABC=360°﹣130°﹣90°﹣40°=100°.
∵BE∥AD,
∴∠ABE=180°﹣∠A=180°﹣130°=50°,
∴∠ABE=∠ABC,即BE平分∠ABC.
9.解:∵AB∥CD,∠1=72°,
∴∠BEF=180°﹣∠1=180°﹣72°=108°,∠2=∠BEG,
∵EG平分∠BEF,
∴∠BEG=∠BEF=×108°=54°,即∠2=54°.
10.解:∵EF∥AD(已知)
∴∠2=∠3(两直线平行,同位角相等);
∵∠1=∠2(已知),
∴∠1=∠3(等量代换);
∴DG∥AB(内错角相等,两直线平行).
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).
∵∠BAC=70°,
∴∠AGD=110°.
( http: / / www.21cnjy.com )
11.解:∠AED=∠ACB.
理由:∵∠1+∠4=180°(平角定义),∠1+∠2=180°(已知).
∴∠2=∠4.
∴EF∥AB(内错角相等,两直线平行).
∴∠3=∠ADE(两直线平行,内错角相等).
∵∠3=∠B(已知),
∴∠B=∠ADE(等量代换).
∴DE∥BC(同位角相等,两直线平行).
∴∠AED=∠ACB(两直线平行,同位角相等).
12.解:∵DE∥BC,∠AED=80°,
∴∠ACB=∠AED=80°(两直线平行,同位角相等),
∵CD平分∠ACB,
∴∠BCD=∠ACB=40°,
∵DE∥BC,
∴∠EDC=∠BCD=40°(两直线平行,内错角相等).
13.证明:∵AD∥BC(已知)
∴∠B=∠EAD(两直线平行,同位角相等)
∠DAC=∠C(两直线平行,内错角相等)
又∵∠B=∠C(已知)
∴∠EAD=∠DAC(等量代换)
∴AD平分∠CAE(角平分线的定义).
14.解:∠A=∠C+∠AFC.理由如下:
如图,
∵AB∥CD,
∴∠A=∠1,
∵∠1=∠C+∠AFC,
∴∠A=∠C+∠AFC.
( http: / / www.21cnjy.com )
15.解:∵MG平分∠BMN(已知)
∴∠GMN=∠BMN(角平分线的定义),
同理∠GNM=∠DNM.
∵AB∥CD(已知),
∴∠BMN+∠DNM=180°,
∴∠GMN+∠GNM=90°,
∵∠GMN+∠GNM+∠G=180°,
∴∠G=90°,
∴MG与NG的位置关系是MG⊥NG;
故答案为:已知;角平分线的定义;已知;180°;90°;180°;90°;MG⊥NG;
(2)两平行直线被第三条直线所截,同旁内角的角平分线互相垂直.
16.解:∵AD∥BC,∠EFG=50°,
∴∠EFC=180°﹣∠EFG=130°,
由折叠的性质可知,∠NFE=∠EFC,∠MEF=∠DEF,
∴∠DEG=100°,
∴∠EGC=180°﹣100°=80°,
则∠BGM=∠EGC=80°(对顶角相等).
17.证明:∵DE∥AC,
∴∠ADE=∠CAD,
∵AD是∠BAC的平分线,
∴∠EAD=∠CAD,
∴∠ADE=∠EAD,
∴AE=DE,
∵BD⊥AD,
∴∠ADE+∠BDE=90°,∠EAD+∠ABD=90°,
∴∠ABD=∠BDE,
∴BE=DE,
∴AE=BE.
18.解:∵CD∥AB,
∴∠BOD=180°﹣∠CDO=180°﹣62°=128°,
∵OE平分∠BOD,
∴∠DOE=∠BOD=×118°=59°,
∵OE⊥OF,
∴∠EOF=90°,
∴∠DOF=∠EOF﹣∠DOE=90°﹣59°=31°.
19.解:∵AB∥CD,
∴∠ABC=∠BCD=45°,
∵EF∥CD,
∴∠FEC+∠ECD=180°,
∵∠CEF=155°,
∴∠ECD=25°,
∴∠BCE=∠BCD﹣∠ECD=20°.
20.证明:∵AB∥EF,
∴∠E=∠AGD,
∵BC∥ED,
∴∠B=∠AGD,
∴∠B=∠E.
21.解:∵AB∥CD,∠EFG=72°(已知)
∴∠BEF=108°(两直线平行,同旁内角互补)
∵EG平分∠BEF,
∴∠BEG=54°(角平分线定义)
∴∠EGF=∠BEG=54°(两直线平行,内错角相等).
22.解:∵AC丄AB,
∴∠BAC=90°,
∵∠1=60°,
∴∠B=180°﹣∠1﹣∠BAC=30°,
∵a∥b,
∴∠2=∠B=30°.
23.证明:∵AB∥CD,
∴∠MEB=∠MFD,
∵EG∥FH,
∴∠MEG=∠MFH,
∴∠MEB﹣∠MEG=∠MFD﹣∠MFH,
即∠1=∠2.
24.解:(1)OA是∠COF的平分线.
∵OE⊥AB,
∴∠AOE=90°,
∵OC恰好是∠AOE的平分线,
∴∠AOC==45°,
∵OF⊥CD,
∴∠COF=90°,
∴∠AOF=∠COF﹣∠AOC=90°﹣45°=45°,
∴OA是∠COF的平分线;
(2)设∠AOC=x,
∴∠BOD=x,
∵∠AOE=90°,
∴∠COE=∠AOE﹣∠AOC=90°﹣x,
∴∠EOF=∠COE+∠COF=90°﹣x+90°=180°﹣x,
∵∠EOF=5∠BOD,
∴180°﹣x=5x,
解得x=30,
∴∠COE=90°﹣30°=60°.
25.解:BC∥EF.
∵△ACB和△DFE中,∠A=∠1,∠C=∠F,
∴∠B=∠E.
∴BC∥EF.
26.证明:∵AB⊥BC,BC⊥CD,
∴∠ABC=∠DCB=90°,
∵∠1=∠2,
∴∠ABC﹣∠1=∠DCB﹣∠2,
∴∠CBE=∠BCF,
∴BE∥CF.
27.解:∵BD平分∠ABC,CE平分∠ACB,
∴∠DBF=∠ABC,∠ECB=∠ACB,
∵∠ABC=∠ACB,
∴∠DBF=∠ECB,
∵∠DBF=∠F,
∴∠ECB=∠F,
∴EC∥DF.
28.解:BC∥DE,
理由如下:
∵BE平分∠ABC,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3,
∴BC∥DE.
29.解: ( http: / / www.21cnjy.com )
∵AB⊥BC,
∴∠ABC=90°,
∴∠1+∠3=90°,
∵∠1=55°,
∴∠3=35°,
∵a∥b,
∴∠2=∠3=35°.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
