6.2黄金分割同步练习（含解析）

中小学教育资源及组卷应用平台
6.2黄金分割
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．如图，是叶脉的黄金分割点，则（ ）

A． B． C． D．
2．若，则的值为（ ）
A． B． C． D．
3．如果线段，，那么和的比例中项是（ ）
A． B． C． D．
4．在比例尺为1：10000000的地图上，量的甲、乙两地的距离是30cm，则两地的实际距离是（ ）
A．30km B．300km C．3000km D．30000km
5．若，则的值是（ ）
A． B． C． D．
6．如果x：y=3：5，那么x：（x+y）=（ ）
A． B． C． D．
7．已知3x=2y，则x，y一定满足（　　）
A．， B．， C． D．
8．如图，在△ABC中，D、E分别是AB、AC上的点，DE∥BC，BE与CD相交于F，则下列结论一定正确的是（ ）．
A． B． C． D．
9．已知点C把线段分成两条线段，，下列说法错误的是（　　）
A．如果，那么线段被点C黄金分割
B．如果，那么线段被点C黄金分割
C．如果线段被点C黄金分割，那么与的比叫做黄金比
D．0.618是黄金比的近似值
10．已知，下列各选项中一定正确的是（ ）
A． B． C． D．
11．如图所示，在中，，若，，则的值为（ ）
A． B． C． D．
12．已知，则（ ）
A． B． C． D．
二、填空题
13．若，则 ．
14．在比例尺为1：100000的地图上，量得甲、乙两地的距离是15cm，则两地的实际距离 km
15．已知，则 ．
16．如图，点P把线段分成两部分，且为与的比例中项．如果，那么 ．
17．点是线段的黄金分割点，，若，则 ．
三、解答题
18．已知，，求、、的值．
19．如图，在下列网格中，横、纵坐标均是整数的点叫格点，例如都是格点．

（1）直接写出的面积；
（2）仅用无刻度的直尺在图中画出一条线段，使它满足以下条件：①点在内；②点都是格点；③三等分；④，请写出点的坐标．
20．某同学为了测量学校围墙边一棵树的高度，他在旁边地面上竖直立着一根长的竹竿，竹竿在阳光下的影子长为1米，同一时刻，这棵树的影子一部分在地上，一部分在围墙上，他测得这棵树在地面上的影子长为6米，在围墙上的影子长为，那么这棵树的高度为多少米？
21．黄金分割具有严格的比例性、艺术性、和谐性，蕴藏着丰富的美学价值，这一比值能够引起人们的美感，被认为是建筑和艺术中最理想的比例．人体上半身长和下半身长的黄金比为，这时人的身长比例看上去更美观．乐乐的妈妈上半身长68厘米，下半身长104厘米，她想通过穿高跟鞋，使身长的比例更美观，于是她购买了一双6厘米高的高跟鞋．依据黄金比，这双高跟鞋的高度合适吗？请说明理由．
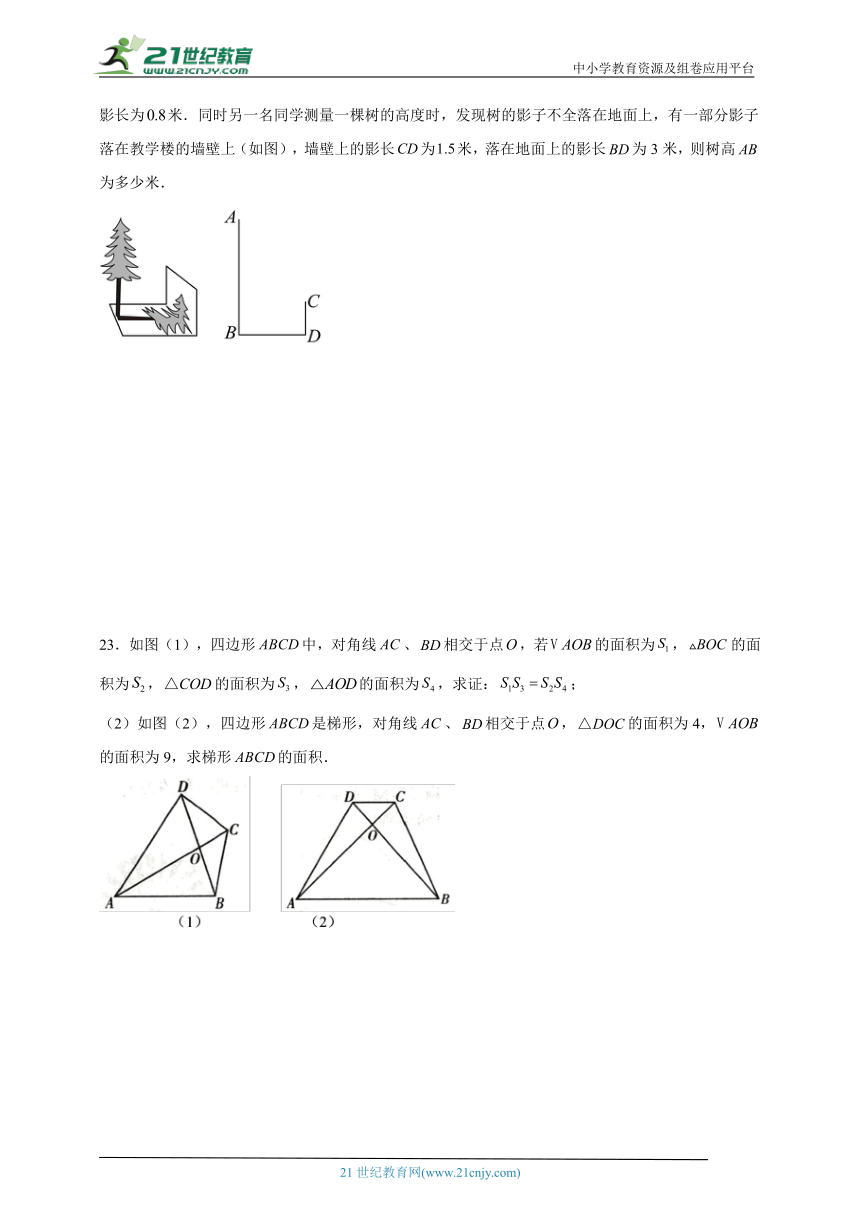
22．如图：小明想测量一棵树的高度，在阳光下，小明测得一根与地面垂直、长为1米的竹竿的影长为米．同时另一名同学测量一棵树的高度时，发现树的影子不全落在地面上，有一部分影子落在教学楼的墙壁上（如图），墙壁上的影长为米，落在地面上的影长为3米，则树高为多少米．
23．如图（1），四边形中，对角线、相交于点，若的面积为，的面积为，的面积为，的面积为，求证：；
（2）如图（2），四边形是梯形，对角线、相交于点，的面积为4，的面积为9，求梯形的面积．
24．如图1，E是正方形ABCD边AB上的一点，连接BD、DE，将∠BDE绕点D逆时针旋转90 ，旋转后角的两边分别与射线BC交于点F和点G．
（1）探究线段BE、BF和DB之间的数量关系，写出结论并给出证明；
（2）当四边形ABCD为菱形，∠ADC=60 ，点E是菱形ABCD边AB所在直线上的一点，连接BD、DE，将∠BDE绕点D逆时针旋转120 ，旋转后角的两边分别与射线BC交于点F和点G．
①如图2，点E在线段AB上时，请探究线段BE、BF和BD之间的数量关系，写出结论并给出证明；
②如图3，点E在线段AB的延长线上时，DE交射线BC于点M．若BE=1，AB=2，直接写出线段GM的长度．
参考答案：
题号 1 2 3 4 5 6 7 8 9 10
答案 A C D C A B C C C B
题号 11 12
答案 C C
1．A
【分析】根据黄金分割数的性质（如果把一条线段分为两部分，使其中较长一段与整个线段的比是黄金分割数，那么较短一段与较长一段的比也是黄金分割数）求解即可．
【详解】根据黄金分割数的性质可知．
故选：A．
【点睛】本题主要考查黄金分割数，牢记黄金分割数的性质（如果把一条线段分为两部分，使其中较长一段与整个线段的比是黄金分割数，那么较短一段与较长一段的比也是黄金分割数）是解题的关键．
2．C
【分析】本题考查了比例的性质，分式的化简求值，掌握比例的内项之积与外项之积相等是解题关键．由可得，再代入化简求值即可．
【详解】解：，
，
，
，
故选：C．
3．D
【分析】由比例中项的概念结合比例的基本性质，得：比例中项的平方等于两条线段的乘积，即可求解．
【详解】解：设它们的比例中项是xcm，根据题意得：
x2=2×18，
解得：（线段是正数，负值舍去）．
故选：D
【点睛】本题主要考查了比例的基本性质，熟练掌握比例中项的平方等于两条线段的乘积是解题的关键．
4．C
【详解】设相距30cm的两地实际距离为xcm，
根据题意得：1：10000000=30：x，
解得：x=300000000，
∵300000000cm=3000km，
∴相距30cm的两地实际距离为3000km．
故选C
5．A
【分析】先化简，再将所给式子带入即可.
【详解】解：化简得，故选：A.
【点睛】本题考查了分式的化简，熟练掌握运用是解决本题的关键.
6．B
【分析】可设x=3k，根据已知条件得到y=5k，再代入计算可求x：（x+y）的值．
【详解】解：∵x：y=3：5，
∴可设x=3k，则y=5k，
则x：（x+y）=3k：（3k+5k）=3：8；
故选：B．
【点睛】本题考查了比例的性质的应用，主要考查学生的计算能力，题目比较好，难度不大．
7．C
【分析】根据两内项之积等于两外项之积解答即可．
【详解】解：∵3x=2y，
∴．
故选C．
【点睛】本题考查了比例的性质，熟记两内项之积等于两外项之积是解题的关键．
8．C
【分析】根据平行线分线段成比例定理及其推论逐项判断即可．
【详解】解：A. ∵DE∥BC，
∴，故错误；
B. ∵DE∥BC，
∴，故错误；
C. ∵DE∥BC，
∴，，
∴，故正确；
D. ∵DE∥BC，
∴，故错误；
故选：C.
【点睛】此题考查了平行线分线段成比例定理，注意掌握各线段的对应关系是解此题的关键．
9．C
【分析】本题属于概念理解类题目，解题的关键是掌握黄金分割的定义“若点C把线段分成两条线段和（），如果，那么称线段被点C黄金分割，点C叫做线段的黄金分割点，与的比叫做黄金比”；根据黄金分割的定义，分别对各个选项进行判断，问题即可得解．
【详解】解：根据黄金分割的定义可知A、B、D正确．
C、如果线段被点C黄金分割（），那么与的比叫做黄金比，所以C错误．
故选：C．
10．B
【分析】本题考查了比例的性质，分式运算．熟练掌握比例的性质是解题的关键．
由题意知，当时，，，，进而可知A、C、D不一定正确，，可知B一定正确，然后作答即可．
【详解】解：∵，
∴当时，，，，A、C、D不一定正确，故不符合要求；
，B一定正确，故符合要求；
故选：B．
11．C
【分析】算出AB后即可得到解答．
【详解】∵，，
∴，
∴
故选：C．
【点睛】本题考查线段的比值，熟练掌握线段的和与差是解题关键 ．
12．C
【分析】把变形为，再根据等的性质可得解．
【详解】解：∵，
∴，
∴，
∴，
∴，
故选：C．
【点睛】本题考查了比例的性质．解题的关键熟练掌握比例式的变形．
13．/0.75
【分析】本题考查比例的性质，主要利用了等比性质，解题的关键是熟练掌握等比性质．
【详解】解：∵，
∴．
故答案为：．
14．15
【详解】解：设两地的实际距离为xcm，
根据题意得：，
解得：x=1500000，
∵1500000cm=15km，
∴两地的实际距离15km．
15．
【分析】本题考查了比例的性质，由，得到，代入即可求解．
【详解】解：，
，
，
故答案为：．
16．/
【分析】根据黄金分割的定义结合已知条件得，即可得出结论．
【详解】解：∵点P把线段分成两部分，且为与的比例中项，
∴，
∴根据黄金分割的定义可得出：，
∴，
故答案为：．
【点睛】本题考查的是黄金分割的概念，把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割．
17．
【分析】根据黄金分割的定义即可进行计算解答．
【详解】点是线段的黄金分割点，且，
，
，
，
故答案为．
【点睛】本题考查了黄金分割的知识，把线段分成两条线段和，且使是和的比例中项，叫做把线段黄金分割．
18．，，
【分析】考查了比例的性质，设k法得到关于k的方程是解题的关键．可设，可得，，，再根据可得关于k的方程，解方程求出k，进一步求得a、b、c的值．
【详解】解：设，
则、、，
∵，
，
，
、、．
19．（1）12；（2）作图见解析，E点坐标为(2,4)，F点坐标为(7,8)
【分析】（1）用长方形的面积减去三个外围的直角三角形面积就可算出△ABC的面积．
（2）利用平行线分线段成比例得出CF∶BE=2,则三等分BC，然后写出E、F的坐标，根据勾股定理求出EF的长度为
【详解】解：（1）△ABC的面积=4×7-×7×1-×3×3-×4×4=12
（2）如图，EF为所做线段，其中E点坐标为(2,4)，F点坐标为(7,8)，EF长度为．

【点睛】本题考查了勾股定理和三角形面积及平行线分线段成比例，熟练掌握相关知识是解题的关键．
20．米
【分析】本题考查了一元一次方程的应用、平行投影、以及比例的性质，设这棵树的高度为x米，再减去围墙上的影子长度，剩余树的长度与地面影子的比即与竹竿的长度与影子的比相同，即可解题．
【详解】解：，，
设这棵树的高度为x米，则，解得（米），
答：这棵树的高度为米．
21．这双高跟鞋合适，理由见解析．
【分析】本题考查了黄金分割，以及比例的性质，根据黄金分割的定义，进行计算即可解答．
【详解】解：这双高跟鞋合适，理由如下：
（），
，
答：这双高跟鞋合适，穿起来后上半身长与下半身长正好成黄金比．
22．米
【分析】本题考查矩形的性质、比例线段．
连接，作，得到四边形为矩形，三角形为直角三角形，设米，利用同一时刻，物体的影长与物高成比例得出方程，然后解方程即可解决问题．
【详解】解：连接，作，
由题意得：，
设米，则
解得：．
∴树高是（米）
答：树高为5.25米．
23．（1）详见解析；（2）25.
【分析】(1)作BE⊥AC于点E，从而可分别表示出 和 然后可得出，同理可得出，这样即可证得结论．
（2）根据同底等高的三角形的面积相等可得出 ，从而解出的面积，也就能得出梯形的面积．
【详解】（1） 作于点，
∴．
同理可证：，
∴．
∴．
（2）∵，
∴（同底等高）．
∴．
设△的面积为，由（1）可得，
∴，
∴梯形的面积．
【点睛】本题考查了梯形，三角形的面积，掌握平行线间距离相等是解题的关键.
24．（1），证明见解析；（2）①，证明见解析；②
【分析】（1）根据旋转的性质可证得△BDG是等腰直角三角形，得到，再证明△FDG≌△EDB（ASA），得到FG=BE即可得到；
（2）①根据菱形的性质以及旋转的性质可得∠DBG=∠G=30°，从而证明△EDB≌△FDG（ASA），得到BF+BE=BF+FG=BG，过点D作DP⊥BG于点P，利用勾股定理及等腰三角形的性质得到BG=，从而得出即可；
②过点A作AN⊥BD交BD于点N，根据含30°直角三角形的性质及等腰三角形的性质，计算BD和BF的长，根据平行线分线段成比例定理可得BM的长，根据线段的差可得结论．
【详解】解：（1），
理由：由旋转可知，∠BDE=∠FDG，∠BDG=90°，
∵四边形ABCD是正方形，
∴∠CBD=45°，
∴∠G=45°，
∴∠G=∠CBD=45°，
∴BD=DG，
△BDG是等腰三角形，
∴，
∵在△FDG与△EDB中，
∠FDG=∠EDB，∠G=∠DBE=45°，BD=DG，
∴△FDG≌△EDB（ASA），
∴FG=BE
∴BE+BF=FG+BF=BG=，
∴
（2）①
理由：如图2，在菱形ABCD中，∠ADB=∠CDB=∠ADC=30°，
由旋转120°可知，∠EDF=∠BDG=120°，∠EDB=∠FDG，
在△DBG中，∠G=180°-120°-30°=30°，
∴∠DBG=∠G=30°，
DB=DG，
∴△EDB≌△FDG（ASA），
∴BE=FD，
∴BF+BE=BF+FG=BG，
过点D作DP⊥BG于点P，
∵BD=DG，∴BG=2BP，
∵∠DBC=30°，
∴DP=，
∴在Rt△BDP中，，
∴BG=
∴
②如图3，过点A作AN⊥BD交BD于点N，
在Rt△ABN中，∠ABN=30°，AB=2，
∴AN=1，BN=，
∴BD=2BN=2，
∵DC∥BE，
∴，
∵CM+BM=2，
∴BM=，
Rt△BDP中，∠DBP=30°，BD=2，
∴BP=3
由旋转得：BD=FD，
∴BF=2BP=6，
∴GM =BG-BM=6+1-=．
【点睛】此题是四边形综合题，主要考查了全等三角形的判定和性质，平行线分线段成比例定理，正方形和菱形的性质，含30度直角三角形的性质等知识，本题证明△FDG≌△BDE是解本题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)