6.3相似图形同步练习（含解析）

中小学教育资源及组卷应用平台
6.3相似图形
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．下列说法正确的有（ ）．
①形状差不多的两个图形相似；②国旗上的大五角星与小五角星是相似的；③大小不等的两个六边形的形状可能相似；④放大镜下看到的图形与原来的图形的相似．
A．1个 B．2个 C．3个 D．4个
2．下列说法正确的是（ ）
A．菱形都相似 B．正六边形都相似
C．矩形都相似 D．一个内角为80°的等腰三角形都相似
3．如图，从图甲到图乙的变换是（ ）
A．轴对称变换 B．平移变换 C．旋转变换 D．相似变换
4．如图,在△ABC中,点D、E分别在AB、AC边上,DE∥BC．若AE:AC=3:4,AD=9,则AB等于（ ）
A．10 B．11 C．12 D．16
5．在如图所示的图形中，形状相同的是（ ）

A．图①与图② B．图②与图③ C．图②与图④ D．图①与图④
6．下列四组图形中一定相似的是（ ）
A．正方形与矩形 B．正方形与菱形
C．等边三角形与等边三角形 D．矩形与矩形
7．如图，一张矩形纸片ABCD的长，宽将纸片对折，折痕为EF，所得矩形AFED与矩形ABCD相似，则a：
A．2：1 B．：1 C．3： D．3：2
8．下列各组图形一定相似的是（ ）
A．所有的等腰三角形都相似 B．所有的等边三角形都相似
C．所有的菱形都相似 D．所有的矩形都相似
9．在下列各组图形中，一定相似的是（ ）
A． B． C． D．
10．顶角为的等腰三角形称为黄金三角形，如图，五边形的条边相等，个内角相等，则图中共有黄金三角形的个数是（ ）
A．25 B．10 C．15 D．20
11．下列说法中，正确的是（ ）
A．所有的等腰三角形都相似
B．所有的菱形都相似
C．所有的矩形都相似
D．所有的等腰直角三角形都相似
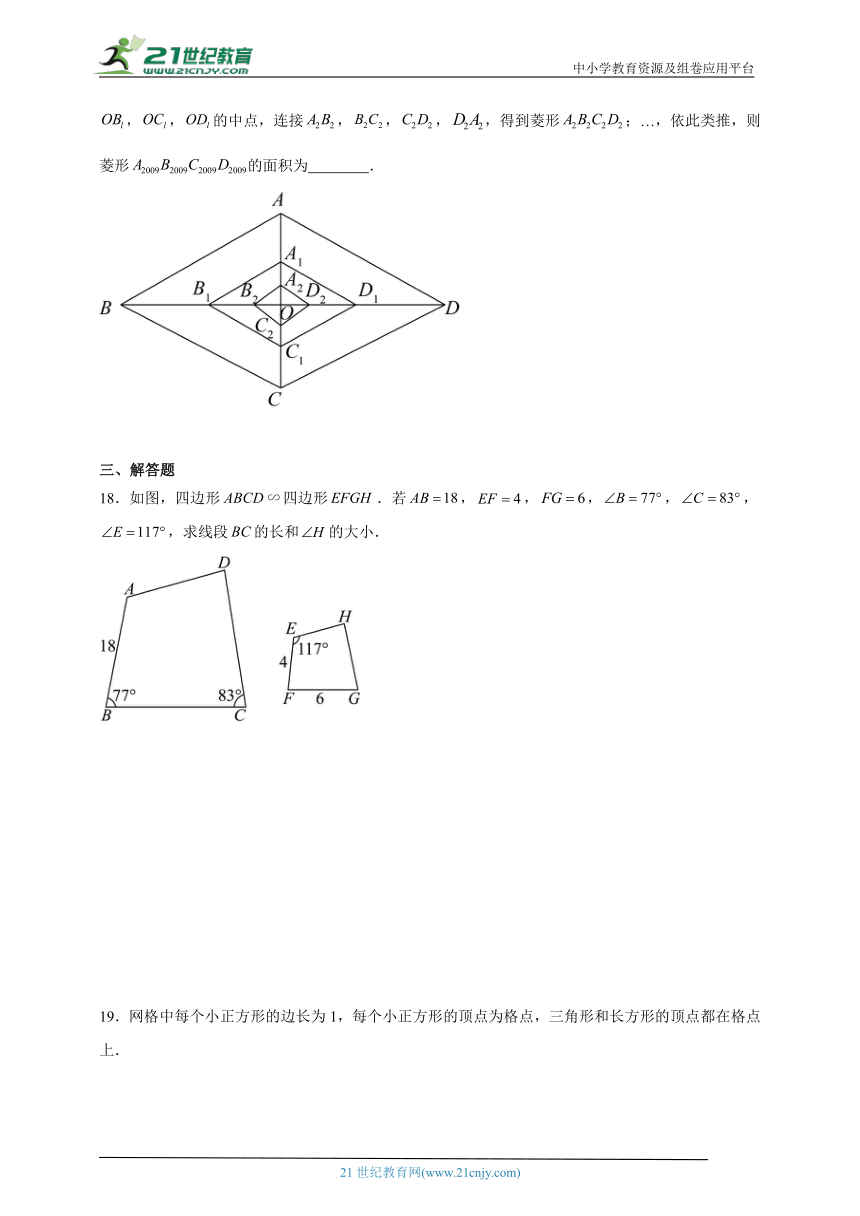
12．下列三个矩形相似的是( )
A．①②和③ B．①和② C．①和③ D．②和③
二、填空题
13．如图，点P在以MN为直径的半圆上运动，（点P与M，N不重合）平分，交PM于点E，交PQ于点F．
(1) ．
(2)若，则 ．
14．如图，四边形是一张矩形纸片.将其按如图所示的方式折叠：使边落在边上，点A落在点H处，折痕为；使边落在边上，点B落在点G处（点H在点G的左侧），折痕为.若矩形与原矩形相似，且，则原矩形的面积为 .
15．沿一张矩形纸较长两边的中点将纸折叠，所得的两个矩形仍然与原来的矩形相似，则原矩形纸的长、宽之比是
16．已知四边形ABCD与四边形A'B'C′D'相似，边AB与边A'B'是对应边，S四边形ABCD：S四边形A'B′C′D′＝2：4，AB＝2，则A'B'＝ ．
17．如图，菱形的面积为，对角线，交于点，点，，，分别是，，，的中点，连接，，，得到菱形；点，，，分别是，，，的中点，连接，，，，得到菱形；…，依此类推，则菱形的面积为 ．
三、解答题
18．如图，四边形四边形．若，，，，，，求线段的长和的大小．
19．网格中每个小正方形的边长为1，每个小正方形的顶点为格点，三角形和长方形的顶点都在格点上．
(1)在图1的网格中按2：1画出网格中三角形放大后的图形①；
(2)在图2的网格中按1：2画出网格中长方形缩小后的图形②；
(3)请直接写出图形①的面积与图形②的面积的最简整数比为 ．
20． 数学社团活动课上，同学们研究一个问题：任意给定一个矩形，是否存在一个新矩形，它的周长和面积分别是原矩形周长和面积的？
【阶段一】同学们认为可以先研究给定矩形为正方形的情况，即是否存在一个正方形，其周长和面积都为原正方形周长和面积的？
思路一：设给定的正方形的边长为a，则其周长为4a，面积为a2． 若新正方形的周长是原正方形周长的，则新正方形的边长为，此时新正方形的面积是____①____．
思路二：正方形是相似图形，周长之比等于相似比，面积之比等于相似比的平方． 如果新正方形的面积是原正方形面积的，则新正方形与原正方形相似比为，此时新正方形周长应是原正方形周长的____②____．
结论：____③____（“存在”或“不存在”）一个新正方形，其周长和面积都为给定正方形周长和面积的．
拓展：除正方形外，上面的结论对哪种图形也成立？请写出一种图形．____④____
【阶段二】同学们对矩形（不包括正方形）的情况进行探究．
活动一：从特殊的矩形入手，如果已知矩形的长和宽分别为4和2，是否存在一个新矩形，它的周长和面积分别是原矩形周长和面积的？
分析：设新矩形长和宽为，，根据题意，得
思路一：消去未知数y，得到关于x的方程，根据方程的解的情况解决问题．
思路二：借助一次函数与反比例函数的图象（画出简单的函数图象即可）研究．
结论：____⑤____（“存在”或“不存在”）一个新矩形，使其周长和面积都是长和宽分别为4和2的矩形周长和面积的．
活动二：对于一般的矩形，如果已知矩形的长和宽分别为m和n，是否存在一个新矩形，它的周长和面积分别是原矩形周长和面积的？若存在，请指出需要满足的条件；若不存在，请说明理由．
请你完成以下任务：
(1)将【阶段一】中的①~④分别补充完整．
(2)分别按照【阶段二】中活动一的思路一、思路二解决问题，并将⑤补充完整．
(3)完成对【阶段二】中活动二的研究．
21．如图，一个矩形休闲广场的长为，宽为，广场内左右两侧的两条纵向人行小路的宽均为3.5m，如果设上下两侧的两条横向人行小路的宽都为m，那么当为多少时，人行小路内外边缘所围成的两个矩形相似？
22．如图，晚上，王叔叔走在大街上，他发现：当他站在大街两边甲、乙两盏路灯（路灯足够亮）之间，并且自己被两边的路灯照在水平干燥地面上的影子成一直线时，甲灯照射的影子长，乙灯照射的影子长，又王叔叔的身高为，两盏路灯的高度相同，路灯相距，求路灯的高．
23．如图，AC∥BD，AD、BC相交于E，EF∥BD，求证： +=．
24．如图，G是正方形ABCD对角线AC上一点，作GE⊥AD，GF⊥AB，垂足分别为点E、F.
求证：四边形AFGE与四边形ABCD相似．

参考答案：
题号 1 2 3 4 5 6 7 8 9 10
答案 C B D C D C B B D D
题号 11 12
答案 D C
1．C
【分析】根据相似图形的定义，对各项进行分析即可得出答案.
【详解】①形状相同的两个图形是相似图形，形状差不多的两个图形，不是相似图形，故①说法错误；
②国旗上的大五角星与小五角星，形状相同，是相似图形，故②说法正确；
③当大小不等两个六边形的对应角相等，对应边成比例式时，这两个六边形相似，故③说法正确；
④放大镜下看到的图形与原来的图形形状相同，是相似图形，故④说法正确；
②③④说法正确，故选C.
【点睛】本题考查相似图形的定义，具有相同形状的图形是相似图形，熟记并理解定义是解决本题的关键.
2．B
【分析】根据相似图形的定义，对选项进行一一分析即可.
【详解】解：A、所有的菱形，边长相等，所以对应边成比例，角不一定对应相等，所以不一定都相似，故本选项错误；
B、所有的正六边形，边长相等，所以对应边成比例，角都是，相等，所以都相似，故本选项正确；
C、所有的矩形，对应角的度数一定相同，但对应边的比值不一定相等，故本选项错误；
D、一个内角为的等腰三角形可能是顶角也可能是底角是，无法判断，此选项错误；
故选B．
【点睛】本题考查的是相似图形的识别，相似图形的形状相同，但大小不一定相同．
3．D
【分析】根据轴对称变换，平移变换，旋转变换，相似变换的定义判断即可．
【详解】解：从图甲到图乙的图形的形状相同，大小不相同，图甲与图乙是相似形，所以从图甲到图乙的变换是相似变换．
故选：D．
【点睛】本题考查轴对称变换，平移变换，旋转变换，相似变换等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．
4．C
【详解】试题解析：∵DE∥BC，
∴，即，
解得：AB=12．
故选C `
5．D
【分析】根据相似图形的定义，对应边成比例，对应角相等，然后对各选项分析判断后利用排除法求解．
【详解】A.图①与图②对应边不一定成比例，所以一定不相似；
B. 图②与图③对应角不相等，所以一定不相似；
C. 图②与图④对应边不一定成比例，所以一定不相似；
D.图①与图④对应边对应边成比例，比例为1：1.5，对应角相等，故选Ｄ
【点睛】本题考查相似图形的定义，解题的关键是掌握相似图形的定义.
6．C
【分析】本题考查了图形的相似，根据相似的定义是图形形状相同，对应边成比例，进行逐项分析，即可作答．
【详解】解：A、正方形与矩形的形状不相同，故该选项是不符合题意；
B、正方形与菱形的形状不相同，故该选项是不符合题意；
C、等边三角形与等边三角形的形状相同，对应边成比例，故该选项是符合题意；
D、矩形与矩形的形状相同，对应边不一定成比例，故该选项是不符合题意；
故选：C
7．B
【分析】根据折叠性质得到AF＝AB＝a，再根据相似多边形的性质得到，即，然后利用比例的性质计算即可．
【详解】解：∵矩形纸片对折，折痕为EF，
∴AF＝AB＝a，
∵矩形AFED与矩形ABCD相似，
∴，即，
∴a∶b＝.
所以答案选B.
【点睛】本题考查了相似多边形的性质：相似多边形对应边的比叫做相似比．相似多边形的对应角相等，对应边的比相等．
8．B
【分析】根据对应角相等，对应边成比例的两个图形，叫做相似图形进行判断即可．
【详解】解：A.任意两个等腰三角形的对应边不一定成比例，不一定相似，A错误；
B.任意两个等边三角形对应角相等、对应边成比例，一定相似，B正确；
C.任意两个菱形的对应角不一定相等，不一定相似，C错误；
D.任意两个矩形的对应边不一定成比例，不一定相似，D错误；
故选B．
【点睛】本题考查的是相似图形的判定，掌握对应角相等，对应边成比例的两个图形，叫做相似图形是解题的关键．
9．D
【分析】根据相似图形的定义，对选项进行一一分析，排除错误答案．
【详解】解：A．形状不相同，不符合相似图形的定义，此选项不符合题意；
B．形状不相同，不符合相似图形的定义，此选项不符合题意；
C．形状不相同，不符合相似图形的定义，此选项不符合题意；
D．形状相同，但大小不同，符合相似图形的定义，此选项符合题意；
故选：D．
【点睛】本题考查的是相似图形的定义，即图形的形状相同，但大小不一定相同的两个图形是相似图形，掌握相似图形的定义是解题的关键．
10．D
【分析】根据正五边形的性质和黄金三角形的定义进行分析．
【详解】根据题意，得
图中的黄金三角形有△BMN、△CNF、△DFG、△EHG、△AMH、△ABN、△CBM、△CDG、△EDF、△AGE、△ACD、△BDE、△CEA、△DBA、△EBC，△NCD，△HDE，△AME，△ABH，△BCF，共20个.
故选:D
【点睛】考查了正五边形的性质和黄金三角形的定义．注意：此图中所有顶角是锐角的等腰三角形都是黄金三角形．
11．D
【分析】根据相似图形的定义，对选项进行一一分析，排除错误答案．
【详解】A、所有的等腰三角形，边的比不一定相等，对应角不一定对应相等，故错误，不符合题意；
B、所有的菱形，边的比一定相等，而对应角不一定对应相等，故错误，不符合题意；
C、所有的矩形，对应角的度数一定相同，但对应边的比值不一定相等，故错误，不符合题意；
D、所有的等腰直角三角形，边的比一定相等，而对应角也对应相等，故正确，符合题意．
故选：D．
【点睛】考查相似多边形的判定，掌握相似多边形的判定定理是解题的关键.
12．C
【详解】相似多边形的特征是对应边的比相等、对应角相等．此题已经具备了对应角相等，只需判断对应边的比是否相等即可．
由题图知，①，②，③，
所以①和③的对应边的比相等．故选C．
13． 1
【分析】(1)过E作于G，可得，根据圆周角的性质可得，又平分，根据角平分线的性质可得；由， ，，且，根据“等角的余角相等”可得 ，再根据等腰三角形的性质“等角对等边”可得，即有；由，，可得，从而可得在中有，将、、代入可得，，既而可求得的值．
【详解】(1)如图所示，过E作于G，则，
∵MN为半圆的直径，
∴，
又∵平分，,
∴．
∵平分，
∴，
∵，
∴,
又，
∴，
又∵，
∴，
∴,
又∵，
∴．
∵，，
∴，
∴在中，,
又∵,
∴，
∴将，，代入得，,
∴，
即．
（2）∵，，
∴，
∴，
∴，
∵，
∴，
∴，
∵，
∴，
∴
∴，即，
设，则，
解得：，或（舍去），
∴，
故答案为：．
【点睛】本题综合考查了圆周角的性质、角平分线的性质、等腰三角形的性质、平行线分线段成比例的性质等知识．(1)中解题的关键是利用角平分线的性质和等腰三角形的性质求得，，再通过平行线分线段成比例的性质得到，进行等量代换和化简后即可得解．
14．
【分析】本题考查矩形的折叠问题、相似多边形的性质等知识点，掌握相似形的性质成为解题的关键．
先根据折叠的性质与矩形性质得，设的长为x，则，再根据相似多边形性质得出，即，可求得x，进而求得,最后求矩形的面积即可．
【详解】解：由折叠可得：，，
∵矩形中，
∴，
设的长为x，则，
∵矩形，
∴，
∵矩形与原矩形相似，
∴，即，解得：（负值不符合题意，舍去）
∴，
∴原矩形的面积为．
故答案为：．
15．
【分析】设原来矩形的长为x，宽为y，先表示出对折后的矩形的长和宽，再根据相似图形对应边成比例列出比例式，然后求解．
【详解】解：设原来矩形的长为x，宽为y，则对折后的矩形的长为y，宽为，
∵得到的两个矩形都和原矩形相似，
∴x：y＝y：，即，
∴x：y＝：1，
故答案为：：1．
【点睛】本题主要考查了相似多边形对应边成比例的性质，表示出对折后的矩形的长和宽是解题关键．
16．2
【分析】利用相似多边形的性质解决问题即可．
【详解】解：∵四边形ABCD与四边形A'B'C′D'相似，边AB与边A'B'是对应边，S四边形ABCD：S四边形A'B′C′D′＝2：4，
∴，
∵AB＝2，
∴A′B′＝2，
故答案为：2．
【点睛】本题考查相似多边形的性质，解题的关键是熟练掌握相似多边形的性质，属于中考常考题型．
17．
【分析】根据面积的比等于相似比的平方进行计算，菱形AlBlClDl的面积等于菱形ABCD的面积的 ，即为；菱形A2B2C2D2的面积等于菱形AlBlClDl的面积的，即，依此类推，则菱形A2009B2009C2009D2009的面积为．
【详解】解：∵点Al，Bl，Cl，Dl分别是OA，OB，OC，OD的中点，
∴＝，
∴菱形AlBlClDl∽菱形ABCD，
∵菱形ABCD的面积为l，
∴菱形AlBlClDl的面积等于，
∴菱形A2B2C2D2的面积等于菱形AlBlClDl的面积的，即，
依此类推，菱形A2009B2009C2009D2009的面积为．
故答案为．
【点睛】本题考查了菱形的相似和性质，注意：相似形的面积的比等于相似比的平方．
18．27，．
【分析】本题考查了相似多边形的性质，根据四边形内角和得出，根据对应边成比例得出的长．
【详解】解：∵四边形四边形
，
∴，，，
∵，
∴，
∵，，，
∴，
∴．
19．(1)图见解析
(2)图见解析
(3)9：4
【分析】（1）原三角形的底和高都是3和3，根据图形放大与缩小的方法，把三角形的底和高按2:1扩大后，得到的是底为6，高为6的三角形，由此可画出这个三角形；
（2）原长方形的长和宽分别是8和4，根据图形变大与缩小的变化方法，把长方形的长和宽按1:2缩小后，得到的是长为4宽为2的长方形，由此可画出这个长方形；
（3）根据三角形的面积=×底×高和长方形面积=长×宽，分别计算出所画图形的面积，然后计算它们的比．
【详解】（1）解：如图1，①即为所求．
（2）解：如图2，②即为所求．
（3）解：①的面积：
②的面积：
面积比：18:8=9:4
∴图形①的面积与图形②的面积最简整数比为9:4．
故答案为：9:4．
【点睛】本题考查图形的放大与缩小（按一定比例把图形放大或缩小，形状不变，边和大小会发生变化，各边的变化都符合指定的比，面积会扩大或者缩小比的平方倍），化简整数比（把比的前项和后项同时除以他们的最大公因数），初步体会图形的相似．解题的关键是理解按2：1放大就是把原图的各边长放大2倍，按1：2缩小就是把原图的各边长乘以及化简比结果是一个比，有比号．
20．(1)①a2；②；③不存在；④等边三角形（答案不唯一，如圆）
(2)思路一：见解析；思路二：见解析；⑤不存在
(3)当时，存在
【分析】
本题考查的是一次函数与反比例函数的灵活应用，矩形，正方形的性质，一元二次方程根的判别式的应用，理解题意，相似多边形的性质，选择合适的方法解题是关键；
（1）①直接利用面积公式计算即可；②由所有的正方形是相似图形，结合相似图形的性质可得答案；③根据②的探究下结论即可；④仿照正方形的探究方法，探究等边三角形即可；
（2）思路一：把方程组消元得到一元二次方程，利用根的判别式的情况可得答案；思路二：分别画出两个函数的简易图象，根据交点的情况判定即可；
（3）根据前面的探究方法建立方程组，根据判别式大于或等于0可得成立的条件．
【详解】（1）解：①新正方形的边长为，此时新正方形的面积是；
②正方形是相似图形，周长之比等于相似比，面积之比等于相似比的平方． 如果新正方形的面积是原正方形面积的，则新正方形与原正方形相似比为，此时新正方形周长应是原正方形周长的；
③总结可得：不存在一个新正方形，其周长和面积都为给定正方形周长和面积的．
④除正方形外，上面的结论对等边三角形也成立；
∵等边三角形都是相似图形，新的等边三角形的面积为原来等边三角形的面积的，
∴新的等边三角形与原来等边三角形的相似比为，
而新的等边三角形的周长为原来等边三角形的周长的，
∴此时新的等边三角形原来等边三角形的相似比为，
∴不存在一个新等边三角形，其周长和面积都为给定等边三角形周长和面积的．
（2）思路一：
设新矩形长和宽为，，根据题意，得
∴，
整理得：，
∴，
∴原方程组无解，则不存在一个新矩形，使其周长和面积都是长和宽分别为4和2的矩形周长和面积的；
思路二：如图，函数与的图象如下：
∵两个函数图象没有交点，
∴无解，
∴不存在一个新矩形，使其周长和面积都是长和宽分别为4和2的矩形周长和面积的；
结论：不存在一个新矩形，使其周长和面积都是长和宽分别为4和2的矩形周长和面积的；
（3）∵矩形的长和宽分别为m和n，
∴矩形的周长为，面积为，
∴新的矩形的周长为，面积为，
设新矩形长和宽为，，
∴，，
∴，
∴，
∴，
∴，
∴，
当时，
存在新矩形，使其周长和面积都是长和宽分别为和的矩形周长和面积的；
21．
【分析】本题考查了相似多边形的性质，关键在于理解相似矩形对应边成比例这一性质，并能准确找出小路内外边缘围成的矩形的长和宽的表达式．
通过分析两个矩形相似的性质，找出对应边的比例关系，并用含有的代数式表示内边缘所围成的矩形的长，进而列方程求解的值即可．
【详解】解：人行小路内边缘所围成的矩形的长为，
宽为．
根据相似多边形定义，当各边成比例时，这两个矩形相似，即：
，
解得，
经检验，是原方程的解．
答：当时，人行小路内外边缘所围成的两个矩形相似．
22．
【分析】根据题意，得，，继而得到，，列比例式，解答即可．
本题考查了中心投影，三角形相似的判定和性质，熟练掌握相似的判定和性质是解题的关键．
【详解】解：根据题意，得，，
∴，，
∴，，
∴，
∵，，
∴
∴，
设，
∵，
∴，
解得，
∴，
∴，
解得，
答：路灯高为．
23．见解析
【详解】试题分析: 由平行线分线段成比例定理得出，，证出=1，即可得出结论．
试题解析:
证明：∵AC∥BD，EF∥BD，
∴，，
∴==1，
∴+=．
24．证明见解析.
【分析】由正方形的性质可知；AC平分∠DAB，然后由角平分线的性质可知GE=GF，从而可证明四边形EGFA为正方形，故此四边形AFGE与四边形ABCD相似；
【详解】解：∵四边形ABCD是正方形，AC是对角线，
∴∠DAC＝∠BAC＝45°.
又∵GE⊥AD，GF⊥AB，
∴EG＝FG，且AE＝EG，AF＝FG.
∴AE＝EG＝FG＝AF，
∴四边形AFGE为正方形．
∴＝＝＝，
且∠EAF＝∠DAB，∠AFG＝∠ABC，∠FGE＝∠BCD，∠AEG＝∠ADC.
∴四边形AFGE与四边形ABCD相似．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)