6.7用相似三角形解决问题同步练习(含解析)
文档属性
| 名称 | 6.7用相似三角形解决问题同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
6.7用相似三角形解决问题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
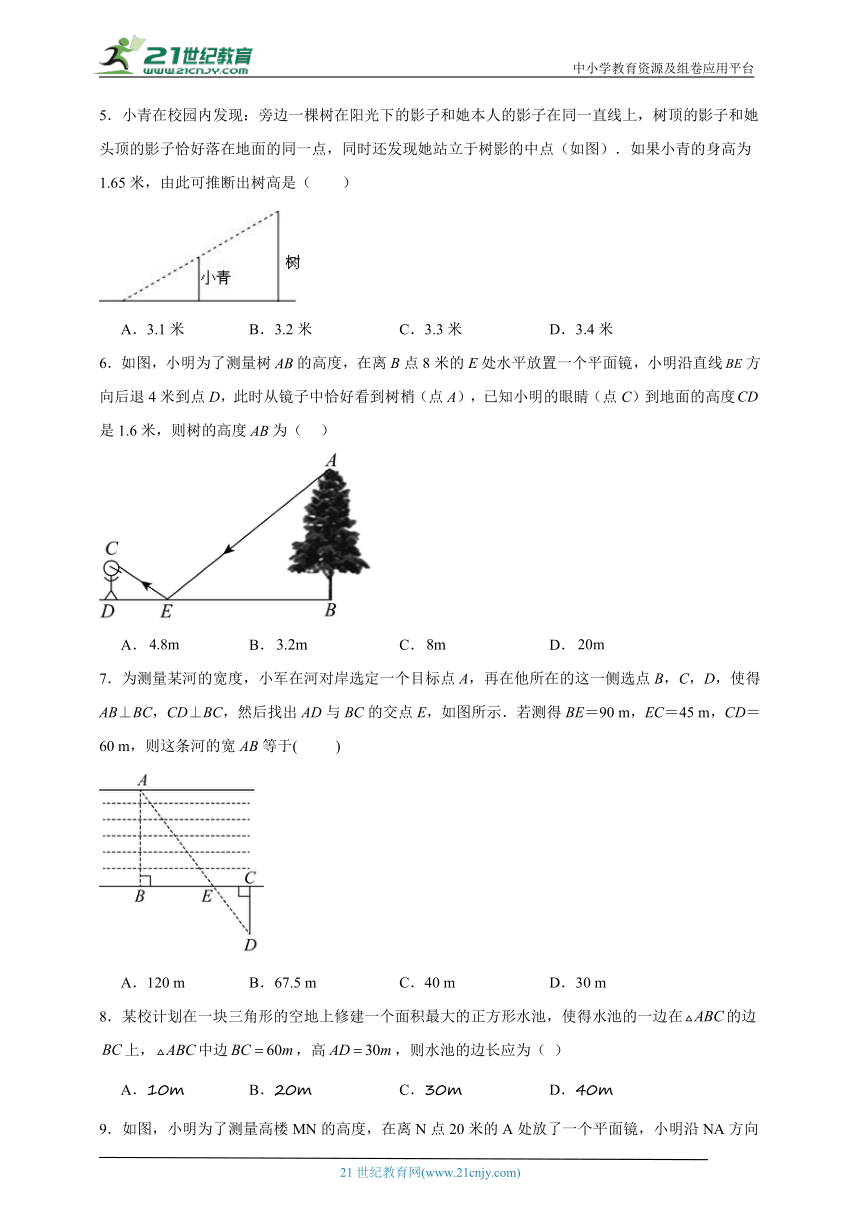
1.如图,有一高度为8m的灯塔AB,在灯光下,身高为1.6m的小亮从距离灯塔底端4.8m的点C处,沿BC方向前进3.2m到达点D处,那么他的影长( )
A.变长了0.8m B.变长了1.2m C.变短了0.8m D.变短了1.2m
2.相同时刻太阳光下,若高为1.5 m的测杆的影长为3 m,则影长为30 m的旗杆的高是( )
A.15 m
B.16 m
C.18 m
D.20 m
3.某校数学兴趣小组为测量学校旗杆的高度,在点F处竖立一根长为米的标杆,如图所示,量出的影子的长度为米,再量出旗杆的影子的长度为米,那么旗杆的高度为( )
A.7米 B.8米 C.9米 D.10米
4.如图,某学生利用标杆测量一棵大树的高度,如果标杆EC的高为2 m,并测得BC=3 m,CA=1 m,那么树DB的高度是( )
A.6m B.8m C.32m D.0.125m
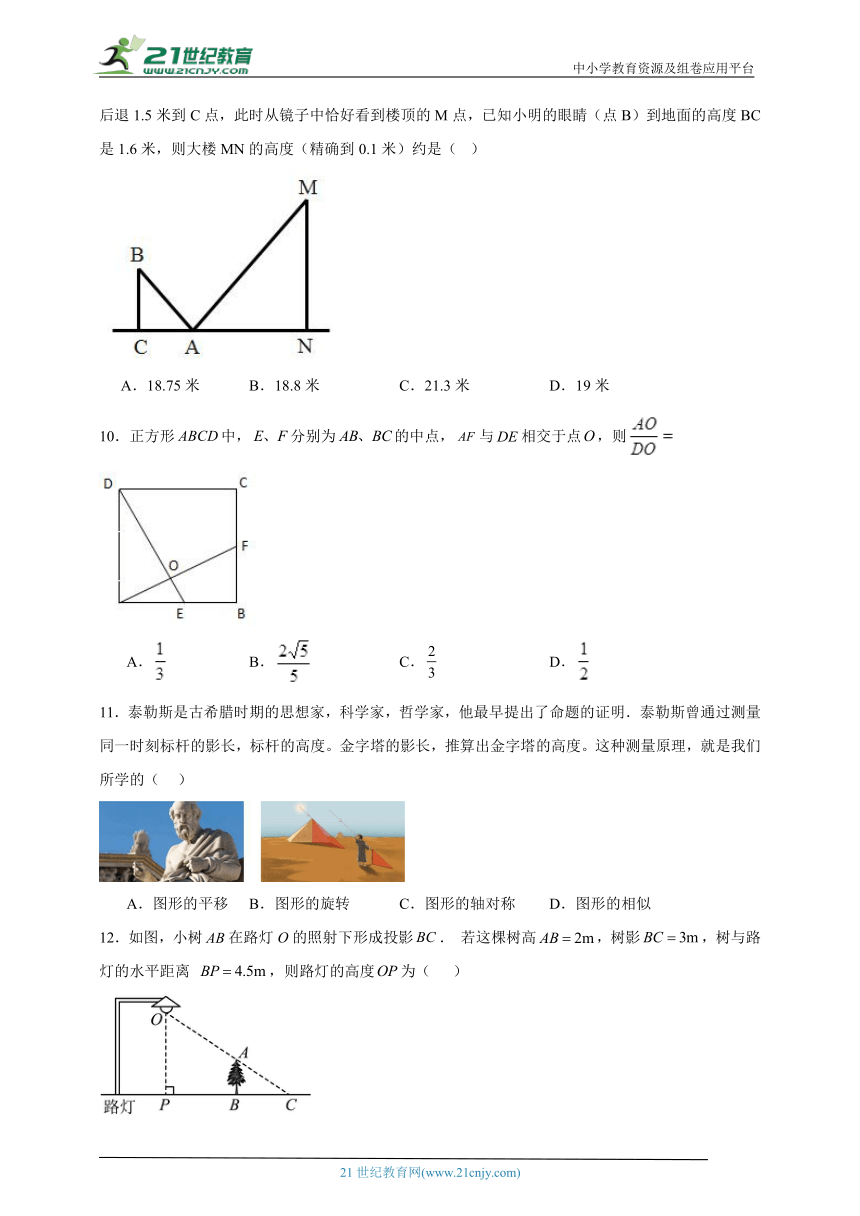
5.小青在校园内发现:旁边一棵树在阳光下的影子和她本人的影子在同一直线上,树顶的影子和她头顶的影子恰好落在地面的同一点,同时还发现她站立于树影的中点(如图).如果小青的身高为1.65米,由此可推断出树高是( )
A.3.1米 B.3.2米 C.3.3米 D.3.4米
6.如图,小明为了测量树的高度,在离B点8米的E处水平放置一个平面镜,小明沿直线方向后退4米到点D,此时从镜子中恰好看到树梢(点A),已知小明的眼睛(点C)到地面的高度是1.6米,则树的高度为( )
A. B. C. D.
7.为测量某河的宽度,小军在河对岸选定一个目标点A,再在他所在的这一侧选点B,C,D,使得AB⊥BC,CD⊥BC,然后找出AD与BC的交点E,如图所示.若测得BE=90 m,EC=45 m,CD=60 m,则这条河的宽AB等于( )
A.120 m B.67.5 m C.40 m D.30 m
8.某校计划在一块三角形的空地上修建一个面积最大的正方形水池,使得水池的一边在的边上,中边,高,则水池的边长应为( )
A.10m B.20m C.30m D.40m
9.如图,小明为了测量高楼MN的高度,在离N点20米的A处放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度(精确到0.1米)约是( )
A.18.75米 B.18.8米 C.21.3米 D.19米
10.正方形中,分别为的中点,与相交于点,则
A. B. C. D.
11.泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的( )
A.图形的平移 B.图形的旋转 C.图形的轴对称 D.图形的相似
12.如图,小树在路灯O的照射下形成投影. 若这棵树高,树影,树与路灯的水平距离 ,则路灯的高度为( )
A.3m B.5m C.6m D.
二、填空题
13.已知,如图矩形的一边在的边上,顶点、分别在边、上,是边上的高,与相交于点,已知,,,则矩形的周长是 .
14.如图,数学实践课上,老师布置任务如下:让小明站在B点处去观测外的位于D点处的一棵大树,所用工具为一个平面镜P和必要的长度测量工具(点B,P,D在同一条直线上).已知小明眼睛距地面,大树高,当小明与平面镜相距 m时,恰好能从平面镜里观测到大树的顶端.
15.《九章算术》中记载了一种测量古井水面以上部分深度的方法,如图所示,在井口A处立一根垂直于井口的木杆,从木杆的顶端B观察井水水岸D.视线与井口的直径交于点E,如果测得米,米,米,那么为 米.
16.如图,地面A处有一盏射灯,小超在A与墙BC之间运动,则他在墙上的投影长度随着他离射灯的距离的变大而 .(填“变大”“变小”或“不变”)
17.如图,在某宽阔平地区域的公园内竖立着两盏相同长度细灯杆,灯杆垂直地面,在点A,B处分别挂着两盏明亮的灯(抽象地看成由一个点发出的光线).小明垂直地面站立在两盏路灯之间(灯杆长度大于小明身高),站立点C与点M,N在同一直线上.小明发现自己在A路灯下的地面影子的最远点E满足,同时自己在B路灯下的地面影子长为,地面影子的最远点F满足,则小明在A路灯下的地面影子长度可以为 .(结果保留根号)
三、解答题
18.小明和小斌在路灯A下在行走,两人想测量一下路灯的高度.两人在站在同一直线BH上,已知小明身高1. 50米,小斌身高1.60米;两人在同一点E处测得小明的影长为1米,小斌向BH方向行走了1米到达D处,测得影长为1.6米,请你帮忙计算出路灯的高度.
19.小红想利用阳光下的影长测量学校旗杆的高度.如图,她在某一时刻在地面上竖直立一个长的标杆,测得其影长.如果的影长,请你在图中完成相关的作图并求出旗杆的高.
20.为了加强视力保护意识,欢欢想在书房里挂一张测试距离为的视力表,但两面墙的距离只有.在一次课题学习课上,欢欢向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲同学设计了一个方案.
甲同学的设计方案
图例
方案 使用平面镜成像的原理来解决房间小的问题.如图,在相距的两面墙上分别悬挂视力表()与平面镜(),由平面镜成像原理,作出了光路图,通过调整人的位置,使得视力表的上、下边沿A,B发出的光线经平面镜的上下边沿反射后射入人眼C处,通过测量视力表的全长()就可以计算出所需镜长.
已知视力表的全长,要使墙面上的镜子能呈现完整的视力表,求镜面长至少为多少米?
21.瑞光塔是位于苏州盘门内的一座宋代古塔,被评为全国重点文物保护单位,,具有很强的历史文化价值.立达数学兴趣小组开展了“测量宝塔高度”的实践活动,在点C处垂直于地面竖立一根高度为2米的标杆,这时地面上的点E,标杆的顶端点D,宝塔的塔尖点B正好在同一直线上,测得米,将标杆向右平移到点G处,这时地面上的点F,标杆的顶端点H,宝塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得米,米.请你根据以上数据计算真身宝塔的高度.
22.法门寺位于炎帝故里、青铜器之乡——宝鸡市扶风县,始建于东汉末年桓灵年间,距今约有1700多年历史,法门寺被誉为“关中塔庙始祖”,其中的“真身宝塔”是全国重点保护文物.某数学兴趣小组开展了“测量真身宝塔高度”的实践活动,在点C处垂直于地面竖立一根高度为2米的标杆,这时地面上的点E,标杆的顶端点D,宝塔的塔尖点B正好在同一直线上,测得米,将标杆向右平移到点G处,这时地面上的点F,标杆的顶端点H,宝塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得米,米.请你根据以上数据,计算真身宝塔的高度.
23.如图1,已知抛物线y=ax2﹣2x+c(a≠0)与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,﹣3),对称轴是直线x=1,△ACB的外接圆M交y轴的正半轴与点D,连结AD、CM,并延长CM交x轴于点E.
(1)求抛物线的函数表达式和直线BC的函数表达式;
(2)求证:△CAD∽△CEB;
(3)如图2,P为x轴正半轴上的一个动点,OP=t,(0<t<3),过P点与y轴平行的直线交抛物线与点Q,若△QAD的面积为S,写出S与t的函数表达式,问:当t为何值时,△QAD的面积最大,且最大面积为多少?
24.如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D B C B A B C D
题号 11 12
答案 D B
1.A
【分析】根据由CH∥AB∥DG可得△HCE∽△ABE、△GDF∽△ABF,所以,将数值代入求解可得CE、DF的值,可得答案.
【详解】解:如图
由CH∥AB∥DG可得△HCE∽△ABE、△GDF∽△ABF,
∴,即
解得:CE=1.2,DF=2
∴DF-CE=2-1.2=0.8
故选A
【点睛】本题考查了相似三角形的应用:利用影长测量物体的高度,通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.
2.A
【分析】根据平行光得出对应线段成比例,即可列出式子解出.
【详解】设旗杆的高是xm,根据题意,得
=,
解得:x=15,
答:旗杆的高是15 m;
故选:A.
【点睛】此题主要考查投影的性质,解题的关键是熟知相似三角形的判断与性质.
3.D
【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.根据相似三角形的对应边的比相等,即可求解.
【详解】解:∵,
,
∴,
即,
米.
故选:D.
【点睛】本题考查了相似三角形在测量高度时的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
4.B
【分析】根据三角形ACE与三角形ABD相似,得到对应边成比例,建立等式求解.
【详解】由题意可得,CE∥BD
∴
有
即
解得BD=8m
故选B.
【点睛】本题考查了相似三角形的判定与性质,在三角形中一平行线平行于第三边,则这个平行线所截的小三角形与原三角形相似,相似三角形对边边成比例.
5.C
【分析】先判断出△ADE∽△ACB,再根据相似三角形的对应边成比例即可得出结论.
【详解】解:∵DE⊥AB,BC⊥AB,
∴△ADE∽△ACB,
∵树顶的影子和她头顶的影子恰好落在地面的同一点,她站立于树影的中点,DE=1.65米,
∴=,
∴BC=2DE=2×1.65=3.3(米).
故选C.
【点睛】本题考查的是相似三角形的应用,熟知相似三角形的对应边成比例是解答此题的关键.
6.B
【分析】本题考查了相似三角形的判定与性质定理,根据相似三角形的判定定理证明,再利用相似三角形的性质求解即可.
【详解】解:由题意得:,,
∴,
由光的反射原理可得:,
∴,
∴,
∵,,,
即,
∴(米).
故选:B.
7.A
【详解】∵∠ABE=∠DCE, ∠AEB=∠CED,
∴△ABE∽△DCE,
∴.
∵BE=90m,EC=45m,CD=60m,
∴
故选A.
8.B
【分析】根据相似三角形的性质即可解答.
【详解】如图:设水池的边长为xm
∵四边形EFGH是正方形
∴EF∥BC
∴△AEF∽△ABC
∴
∴(30-x):30=x:60
∴x=20m
∴水池的边长应为20m.
故选B.
【点睛】本题考查了相似三角形的实际应用,根据对应高线的比等于相似三角形的相似比,列出方程,即可得出水池的边长.
9.C
【分析】由图可先推出,再根据相似三角形的性质求解即可得.
【详解】由镜面反射的规律得:
又
由题意得:
解得:
故选:C.
【点睛】本题考查了相似三角形的判定定理与性质,根据镜面反射的规律得出是解题关键.
10.D
【详解】根据题意,AE=BF,AD=AB,∠EAD=∠B=90°,∴△ADE≌△BAF.
∴∠ADE=∠BAF,∠AED=∠BFA.又∵∠DAO=∠BFA,∴∠DAO=∠AED.∴△AOD∽△EAD.
所以.故选D.
11.D
【分析】根据在同一时刻的太阳光下物体的影长和物体的实际高度成比例即可判断;
【详解】根据题意画出如下图形:可以得到,则
即为金字塔的高度,即为标杆的高度,通过测量影长即可求出金字塔的高度
故选:D.
【点睛】本题主要考查将实际问题数学化,根据实际情况画出图形即可求解.
12.B
【分析】先求解,再根据相似三角形的判定证出,然后利用相似三角形的性质求解即可得.
【详解】解:,,
,
由题意得:,
,
,而,
,即,
解得,
答:路灯的高度为.
故选B
【点睛】本题考查了相似三角形的应用,熟练掌握相似三角形的判定与性质是解题关键.
13.18
【分析】设,则,AK=6-x,根据相似三角形的对应高之比等于相似比得出比例式求解.
【详解】根据题意,设,则, AK=6-x
则,
解得
矩形的周长为
【点睛】本题考查相似三角形的性质应用,掌握相似三角形对应高之比等于相似比是关键.
14.2
【分析】根据平面镜的反射原理:入射角等于入射角证明,利用相似三角形的性质求解即可.
【详解】解:由题意,得,,,
∴,
∴,
∵,,,
∴,
解得,
故小明与平面镜相距时,恰好能从平面镜里观测到大树的顶端.
故答案为:2.
【点睛】本题考查相似三角形的应用,理解题意,掌握平面镜得原理,会利用相似三角形的性质解决实际问题是解答的关键.
15.6
【分析】本题考查了相似三角形的应用,由题意知:,得出对应边成比例即可得出.
【详解】解:由题意知:,
∴,,
∴,
∴,
∴,
∴,
经检验,是所列方程的解,
故答案为:6.
16.变小
【分析】利用相似三角形的性质可得影长BD与小超离光源的距离AF是反比例函数关系,从而可作出选择.
【详解】解:如图所示:
∵EF∥BD,
∴△AEF∽△ADB,
∴
∴.
∵光源与墙BC的距离AB为定值,小超的身高EF也为定值,
∴EF AB是定值,记为k,
则,
∴影长BD与小超离光源的距离AF是比例函数关系,
即小超在墙上的投影长度随着他离射灯的距离的变大而变小.
故答案为:变小.
【点睛】本题考查了投影及相似三角形的应用,根据相似三角形的性质得出影长与离光源的远近是反比例函数关系,即垂直于地面的物体离光源越近,影长越长;离光源越远,影长越短.学会用数学思考问题是解答的关键.
17.,
【分析】由题意可得、,然后再证明可得进而得到,然后分当E在N的左侧和右侧两种情况解答即可.
【详解】解:由题意可得:、
∵,
∴,
∴,
∴
∵
∴
①如图:当E在N的左侧、F在M的左侧时
∵,
∴
设,则,解得:(舍去负值);
②如图:当E在N的右侧、F在N的左侧时,
∵,,
∴,
设,则,解得:(舍去负值).
③如图:当E在N的左侧,F在M的左侧时,
∵,,
∴,
设,则,解得:(舍去负值).
④如图:当E在N的右侧、F在M的左侧时,
∵,,,
∴,
设,则,解得:(舍去负值).
∴.
综上,小明在A路灯下的地面影子长度可以为,.
故答案为,.
【点睛】本题主要考查相似三角形的应用,掌握分类讨论思想是解答本题的关键.
18.4.8
【分析】利用在Rt△A BC中,∠ABC=90°,AB∥DG,得到ΔCDG ΔCBA,进而得到
同理可得: ,将值代入可得AB与BE值.
【详解】在Rt△A BC中,∠ABC=90°,,
∴ΔCDG ΔCBA
同理可得:
解得AB=4.8,BE=2.2
故路灯高为4.8米.
【点睛】本题考查了相似三角形的应用:通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.
19.图见解析,
【分析】本题考查平行线作图,以及相似三角形的性质和判定,解题的关键是根据题意画出图形,并结合及相似三角形的性质和判定解决问题.根据题意连接,过点作的平行线交于点即可,再根据题意证明,最后利用相似三角形性质求解,即可解题.
【详解】解:根据题意作图如下:
由题知,,,
,
,
,
,,,
,
解得.
20.
【分析】此题考查了相似三角形的判定和性质,证明,则,由,则,即可求出即可.
【详解】解:如图,作于点D,延长线交于点E,
由题意知,,
∵,,
∴,
∵,
∴,,
∴
∴,
由题意知,,,
∴,
∴,
∴.
∴镜长至少为
21.米
【分析】本题考查了相似三角形的应用.熟练掌握相似三角形的应用是解题的关键.
由题意知,,,,则,,证明,则,即,可求,同理,则,即,可求,由,可得,计算求解即可.
【详解】解:由题意知,,,,
∴,,
∵,
∴,,
∴,
∴,即,
解得,,
同理,
∴,即,
∴,
∵,
∴,
解得,,
∴真身宝塔的高度为米.
22.47米
【分析】本题考查相似三角形的应用,解题的关键是灵活运用所学知识解决问题,学会构建方程解决问题.先证明,利用相似比得到,再证明,利用相似比得到,利用等量代换得到,进而得到,解得的长,据此求解即可求出的长.
【详解】解:由题知,,,
,
.
由题知,,,
,
.
,
.
米,米,米,
,
米.
,
,
米,
答:真身宝塔的高度为47米.
23.(1),BC:;(2)见解析;(3),时,.
【分析】(1)先根据图像得到a,c的值,进而可得到A、B两点的坐标,再求出函数解析式即可;(2)如图,连结AM,根据同弧所对的圆周角相等得到∠ADC=∠ABC=45°,根据圆周角定理可得∠AMC=90°,进而得到∠ACE=45°,所以∠ACD =∠ECB=45°-∠ECD,即可证明△ACD∽△ECB;(3)根据题意易得△AOF∽△APQ,再根据对应边成比例得到OF与PQ的关系,将Q点横坐标代入抛物线方程求出PQ的长度,进而求出OF的长度,再根据S=S△ADF+S△QDF求出S与t的函数表达式,再求出最大值即可.
【详解】解:(1)∵抛物线的对称轴是x=1,
∴=1,∴a=1
由图像易知c=-3,所以抛物线解析式为, B(3,0),A(-1,0),C(0,-3)
设直线BC的函数表达式为:y=kx+b,
则,解得:k=1,b=-3,
∴直线BC的解析式为 ;
(2)如图,连结AM,
∵OB=OC,∴∠OCB=∠OBC=45°,
∴∠ADC =∠OBC=45°,∠AMC=90°,
又∵AM=CM,∴∠ACE=45°,
∴∠ACD =∠ECB=45°-∠ECD,
∴△ACD∽△ECB
(3)∵PQ∥y轴,∴△AOF∽△APQ,
∴.
∴,
∵PQ=,∴,
∴S=S△ADF+S△QDF=
整理得,
化为顶点式得S=﹣(t-)2+,∴当 .
【点睛】本题主要考查一次函数的图像与性质、二次函数的图像与性质、相似三角形的判定与性质、圆的相关性质,熟练掌握这些知识点并灵活运用,掌握数形结合的思想,是解答的关键.
24.(1)证明见解析;
(2)CF的长度是169cm.
【详解】试题分析:(1)利用“两角法”证得这两个三角形相似;
(2)由△BEF∽△CDF,根据相似三角形的对应边成比例来求线段CF的长度.
试题解析:(1)在矩形ABCD中,由对称性可得出:∠DFC=∠EFB,∠EBF=∠FCD=90°,
∴△BEF∽△CDF;
(2)∵△BEF∽△CDF.
∴,即,
解得:CF=169.
即:CF的长度是169cm.
考点:相似三角形的应用.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
6.7用相似三角形解决问题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,有一高度为8m的灯塔AB,在灯光下,身高为1.6m的小亮从距离灯塔底端4.8m的点C处,沿BC方向前进3.2m到达点D处,那么他的影长( )
A.变长了0.8m B.变长了1.2m C.变短了0.8m D.变短了1.2m
2.相同时刻太阳光下,若高为1.5 m的测杆的影长为3 m,则影长为30 m的旗杆的高是( )
A.15 m
B.16 m
C.18 m
D.20 m
3.某校数学兴趣小组为测量学校旗杆的高度,在点F处竖立一根长为米的标杆,如图所示,量出的影子的长度为米,再量出旗杆的影子的长度为米,那么旗杆的高度为( )
A.7米 B.8米 C.9米 D.10米
4.如图,某学生利用标杆测量一棵大树的高度,如果标杆EC的高为2 m,并测得BC=3 m,CA=1 m,那么树DB的高度是( )
A.6m B.8m C.32m D.0.125m
5.小青在校园内发现:旁边一棵树在阳光下的影子和她本人的影子在同一直线上,树顶的影子和她头顶的影子恰好落在地面的同一点,同时还发现她站立于树影的中点(如图).如果小青的身高为1.65米,由此可推断出树高是( )
A.3.1米 B.3.2米 C.3.3米 D.3.4米
6.如图,小明为了测量树的高度,在离B点8米的E处水平放置一个平面镜,小明沿直线方向后退4米到点D,此时从镜子中恰好看到树梢(点A),已知小明的眼睛(点C)到地面的高度是1.6米,则树的高度为( )
A. B. C. D.
7.为测量某河的宽度,小军在河对岸选定一个目标点A,再在他所在的这一侧选点B,C,D,使得AB⊥BC,CD⊥BC,然后找出AD与BC的交点E,如图所示.若测得BE=90 m,EC=45 m,CD=60 m,则这条河的宽AB等于( )
A.120 m B.67.5 m C.40 m D.30 m
8.某校计划在一块三角形的空地上修建一个面积最大的正方形水池,使得水池的一边在的边上,中边,高,则水池的边长应为( )
A.10m B.20m C.30m D.40m
9.如图,小明为了测量高楼MN的高度,在离N点20米的A处放了一个平面镜,小明沿NA方向后退1.5米到C点,此时从镜子中恰好看到楼顶的M点,已知小明的眼睛(点B)到地面的高度BC是1.6米,则大楼MN的高度(精确到0.1米)约是( )
A.18.75米 B.18.8米 C.21.3米 D.19米
10.正方形中,分别为的中点,与相交于点,则
A. B. C. D.
11.泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的( )
A.图形的平移 B.图形的旋转 C.图形的轴对称 D.图形的相似
12.如图,小树在路灯O的照射下形成投影. 若这棵树高,树影,树与路灯的水平距离 ,则路灯的高度为( )
A.3m B.5m C.6m D.
二、填空题
13.已知,如图矩形的一边在的边上,顶点、分别在边、上,是边上的高,与相交于点,已知,,,则矩形的周长是 .
14.如图,数学实践课上,老师布置任务如下:让小明站在B点处去观测外的位于D点处的一棵大树,所用工具为一个平面镜P和必要的长度测量工具(点B,P,D在同一条直线上).已知小明眼睛距地面,大树高,当小明与平面镜相距 m时,恰好能从平面镜里观测到大树的顶端.
15.《九章算术》中记载了一种测量古井水面以上部分深度的方法,如图所示,在井口A处立一根垂直于井口的木杆,从木杆的顶端B观察井水水岸D.视线与井口的直径交于点E,如果测得米,米,米,那么为 米.
16.如图,地面A处有一盏射灯,小超在A与墙BC之间运动,则他在墙上的投影长度随着他离射灯的距离的变大而 .(填“变大”“变小”或“不变”)
17.如图,在某宽阔平地区域的公园内竖立着两盏相同长度细灯杆,灯杆垂直地面,在点A,B处分别挂着两盏明亮的灯(抽象地看成由一个点发出的光线).小明垂直地面站立在两盏路灯之间(灯杆长度大于小明身高),站立点C与点M,N在同一直线上.小明发现自己在A路灯下的地面影子的最远点E满足,同时自己在B路灯下的地面影子长为,地面影子的最远点F满足,则小明在A路灯下的地面影子长度可以为 .(结果保留根号)
三、解答题
18.小明和小斌在路灯A下在行走,两人想测量一下路灯的高度.两人在站在同一直线BH上,已知小明身高1. 50米,小斌身高1.60米;两人在同一点E处测得小明的影长为1米,小斌向BH方向行走了1米到达D处,测得影长为1.6米,请你帮忙计算出路灯的高度.
19.小红想利用阳光下的影长测量学校旗杆的高度.如图,她在某一时刻在地面上竖直立一个长的标杆,测得其影长.如果的影长,请你在图中完成相关的作图并求出旗杆的高.
20.为了加强视力保护意识,欢欢想在书房里挂一张测试距离为的视力表,但两面墙的距离只有.在一次课题学习课上,欢欢向全班同学征集“解决空间过小,如何放置视力表问题”的方案,其中甲同学设计了一个方案.
甲同学的设计方案
图例
方案 使用平面镜成像的原理来解决房间小的问题.如图,在相距的两面墙上分别悬挂视力表()与平面镜(),由平面镜成像原理,作出了光路图,通过调整人的位置,使得视力表的上、下边沿A,B发出的光线经平面镜的上下边沿反射后射入人眼C处,通过测量视力表的全长()就可以计算出所需镜长.
已知视力表的全长,要使墙面上的镜子能呈现完整的视力表,求镜面长至少为多少米?
21.瑞光塔是位于苏州盘门内的一座宋代古塔,被评为全国重点文物保护单位,,具有很强的历史文化价值.立达数学兴趣小组开展了“测量宝塔高度”的实践活动,在点C处垂直于地面竖立一根高度为2米的标杆,这时地面上的点E,标杆的顶端点D,宝塔的塔尖点B正好在同一直线上,测得米,将标杆向右平移到点G处,这时地面上的点F,标杆的顶端点H,宝塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得米,米.请你根据以上数据计算真身宝塔的高度.
22.法门寺位于炎帝故里、青铜器之乡——宝鸡市扶风县,始建于东汉末年桓灵年间,距今约有1700多年历史,法门寺被誉为“关中塔庙始祖”,其中的“真身宝塔”是全国重点保护文物.某数学兴趣小组开展了“测量真身宝塔高度”的实践活动,在点C处垂直于地面竖立一根高度为2米的标杆,这时地面上的点E,标杆的顶端点D,宝塔的塔尖点B正好在同一直线上,测得米,将标杆向右平移到点G处,这时地面上的点F,标杆的顶端点H,宝塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得米,米.请你根据以上数据,计算真身宝塔的高度.
23.如图1,已知抛物线y=ax2﹣2x+c(a≠0)与x轴交于A、B两点(A点在B点左侧),与y轴交于点C(0,﹣3),对称轴是直线x=1,△ACB的外接圆M交y轴的正半轴与点D,连结AD、CM,并延长CM交x轴于点E.
(1)求抛物线的函数表达式和直线BC的函数表达式;
(2)求证:△CAD∽△CEB;
(3)如图2,P为x轴正半轴上的一个动点,OP=t,(0<t<3),过P点与y轴平行的直线交抛物线与点Q,若△QAD的面积为S,写出S与t的函数表达式,问:当t为何值时,△QAD的面积最大,且最大面积为多少?
24.如图,矩形ABCD为台球桌面,AD=260cm,AB=130cm,球目前在E点位置,AE=60cm.如果小丁瞄准BC边上的点F将球打过去,经过反弹后,球刚好弹到D点位置.
(1)求证:△BEF∽△CDF;
(2)求CF的长.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 A A D B C B A B C D
题号 11 12
答案 D B
1.A
【分析】根据由CH∥AB∥DG可得△HCE∽△ABE、△GDF∽△ABF,所以,将数值代入求解可得CE、DF的值,可得答案.
【详解】解:如图
由CH∥AB∥DG可得△HCE∽△ABE、△GDF∽△ABF,
∴,即
解得:CE=1.2,DF=2
∴DF-CE=2-1.2=0.8
故选A
【点睛】本题考查了相似三角形的应用:利用影长测量物体的高度,通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.
2.A
【分析】根据平行光得出对应线段成比例,即可列出式子解出.
【详解】设旗杆的高是xm,根据题意,得
=,
解得:x=15,
答:旗杆的高是15 m;
故选:A.
【点睛】此题主要考查投影的性质,解题的关键是熟知相似三角形的判断与性质.
3.D
【分析】在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似.根据相似三角形的对应边的比相等,即可求解.
【详解】解:∵,
,
∴,
即,
米.
故选:D.
【点睛】本题考查了相似三角形在测量高度时的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.
4.B
【分析】根据三角形ACE与三角形ABD相似,得到对应边成比例,建立等式求解.
【详解】由题意可得,CE∥BD
∴
有
即
解得BD=8m
故选B.
【点睛】本题考查了相似三角形的判定与性质,在三角形中一平行线平行于第三边,则这个平行线所截的小三角形与原三角形相似,相似三角形对边边成比例.
5.C
【分析】先判断出△ADE∽△ACB,再根据相似三角形的对应边成比例即可得出结论.
【详解】解:∵DE⊥AB,BC⊥AB,
∴△ADE∽△ACB,
∵树顶的影子和她头顶的影子恰好落在地面的同一点,她站立于树影的中点,DE=1.65米,
∴=,
∴BC=2DE=2×1.65=3.3(米).
故选C.
【点睛】本题考查的是相似三角形的应用,熟知相似三角形的对应边成比例是解答此题的关键.
6.B
【分析】本题考查了相似三角形的判定与性质定理,根据相似三角形的判定定理证明,再利用相似三角形的性质求解即可.
【详解】解:由题意得:,,
∴,
由光的反射原理可得:,
∴,
∴,
∵,,,
即,
∴(米).
故选:B.
7.A
【详解】∵∠ABE=∠DCE, ∠AEB=∠CED,
∴△ABE∽△DCE,
∴.
∵BE=90m,EC=45m,CD=60m,
∴
故选A.
8.B
【分析】根据相似三角形的性质即可解答.
【详解】如图:设水池的边长为xm
∵四边形EFGH是正方形
∴EF∥BC
∴△AEF∽△ABC
∴
∴(30-x):30=x:60
∴x=20m
∴水池的边长应为20m.
故选B.
【点睛】本题考查了相似三角形的实际应用,根据对应高线的比等于相似三角形的相似比,列出方程,即可得出水池的边长.
9.C
【分析】由图可先推出,再根据相似三角形的性质求解即可得.
【详解】由镜面反射的规律得:
又
由题意得:
解得:
故选:C.
【点睛】本题考查了相似三角形的判定定理与性质,根据镜面反射的规律得出是解题关键.
10.D
【详解】根据题意,AE=BF,AD=AB,∠EAD=∠B=90°,∴△ADE≌△BAF.
∴∠ADE=∠BAF,∠AED=∠BFA.又∵∠DAO=∠BFA,∴∠DAO=∠AED.∴△AOD∽△EAD.
所以.故选D.
11.D
【分析】根据在同一时刻的太阳光下物体的影长和物体的实际高度成比例即可判断;
【详解】根据题意画出如下图形:可以得到,则
即为金字塔的高度,即为标杆的高度,通过测量影长即可求出金字塔的高度
故选:D.
【点睛】本题主要考查将实际问题数学化,根据实际情况画出图形即可求解.
12.B
【分析】先求解,再根据相似三角形的判定证出,然后利用相似三角形的性质求解即可得.
【详解】解:,,
,
由题意得:,
,
,而,
,即,
解得,
答:路灯的高度为.
故选B
【点睛】本题考查了相似三角形的应用,熟练掌握相似三角形的判定与性质是解题关键.
13.18
【分析】设,则,AK=6-x,根据相似三角形的对应高之比等于相似比得出比例式求解.
【详解】根据题意,设,则, AK=6-x
则,
解得
矩形的周长为
【点睛】本题考查相似三角形的性质应用,掌握相似三角形对应高之比等于相似比是关键.
14.2
【分析】根据平面镜的反射原理:入射角等于入射角证明,利用相似三角形的性质求解即可.
【详解】解:由题意,得,,,
∴,
∴,
∵,,,
∴,
解得,
故小明与平面镜相距时,恰好能从平面镜里观测到大树的顶端.
故答案为:2.
【点睛】本题考查相似三角形的应用,理解题意,掌握平面镜得原理,会利用相似三角形的性质解决实际问题是解答的关键.
15.6
【分析】本题考查了相似三角形的应用,由题意知:,得出对应边成比例即可得出.
【详解】解:由题意知:,
∴,,
∴,
∴,
∴,
∴,
经检验,是所列方程的解,
故答案为:6.
16.变小
【分析】利用相似三角形的性质可得影长BD与小超离光源的距离AF是反比例函数关系,从而可作出选择.
【详解】解:如图所示:
∵EF∥BD,
∴△AEF∽△ADB,
∴
∴.
∵光源与墙BC的距离AB为定值,小超的身高EF也为定值,
∴EF AB是定值,记为k,
则,
∴影长BD与小超离光源的距离AF是比例函数关系,
即小超在墙上的投影长度随着他离射灯的距离的变大而变小.
故答案为:变小.
【点睛】本题考查了投影及相似三角形的应用,根据相似三角形的性质得出影长与离光源的远近是反比例函数关系,即垂直于地面的物体离光源越近,影长越长;离光源越远,影长越短.学会用数学思考问题是解答的关键.
17.,
【分析】由题意可得、,然后再证明可得进而得到,然后分当E在N的左侧和右侧两种情况解答即可.
【详解】解:由题意可得:、
∵,
∴,
∴,
∴
∵
∴
①如图:当E在N的左侧、F在M的左侧时
∵,
∴
设,则,解得:(舍去负值);
②如图:当E在N的右侧、F在N的左侧时,
∵,,
∴,
设,则,解得:(舍去负值).
③如图:当E在N的左侧,F在M的左侧时,
∵,,
∴,
设,则,解得:(舍去负值).
④如图:当E在N的右侧、F在M的左侧时,
∵,,,
∴,
设,则,解得:(舍去负值).
∴.
综上,小明在A路灯下的地面影子长度可以为,.
故答案为,.
【点睛】本题主要考查相似三角形的应用,掌握分类讨论思想是解答本题的关键.
18.4.8
【分析】利用在Rt△A BC中,∠ABC=90°,AB∥DG,得到ΔCDG ΔCBA,进而得到
同理可得: ,将值代入可得AB与BE值.
【详解】在Rt△A BC中,∠ABC=90°,,
∴ΔCDG ΔCBA
同理可得:
解得AB=4.8,BE=2.2
故路灯高为4.8米.
【点睛】本题考查了相似三角形的应用:通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.
19.图见解析,
【分析】本题考查平行线作图,以及相似三角形的性质和判定,解题的关键是根据题意画出图形,并结合及相似三角形的性质和判定解决问题.根据题意连接,过点作的平行线交于点即可,再根据题意证明,最后利用相似三角形性质求解,即可解题.
【详解】解:根据题意作图如下:
由题知,,,
,
,
,
,,,
,
解得.
20.
【分析】此题考查了相似三角形的判定和性质,证明,则,由,则,即可求出即可.
【详解】解:如图,作于点D,延长线交于点E,
由题意知,,
∵,,
∴,
∵,
∴,,
∴
∴,
由题意知,,,
∴,
∴,
∴.
∴镜长至少为
21.米
【分析】本题考查了相似三角形的应用.熟练掌握相似三角形的应用是解题的关键.
由题意知,,,,则,,证明,则,即,可求,同理,则,即,可求,由,可得,计算求解即可.
【详解】解:由题意知,,,,
∴,,
∵,
∴,,
∴,
∴,即,
解得,,
同理,
∴,即,
∴,
∵,
∴,
解得,,
∴真身宝塔的高度为米.
22.47米
【分析】本题考查相似三角形的应用,解题的关键是灵活运用所学知识解决问题,学会构建方程解决问题.先证明,利用相似比得到,再证明,利用相似比得到,利用等量代换得到,进而得到,解得的长,据此求解即可求出的长.
【详解】解:由题知,,,
,
.
由题知,,,
,
.
,
.
米,米,米,
,
米.
,
,
米,
答:真身宝塔的高度为47米.
23.(1),BC:;(2)见解析;(3),时,.
【分析】(1)先根据图像得到a,c的值,进而可得到A、B两点的坐标,再求出函数解析式即可;(2)如图,连结AM,根据同弧所对的圆周角相等得到∠ADC=∠ABC=45°,根据圆周角定理可得∠AMC=90°,进而得到∠ACE=45°,所以∠ACD =∠ECB=45°-∠ECD,即可证明△ACD∽△ECB;(3)根据题意易得△AOF∽△APQ,再根据对应边成比例得到OF与PQ的关系,将Q点横坐标代入抛物线方程求出PQ的长度,进而求出OF的长度,再根据S=S△ADF+S△QDF求出S与t的函数表达式,再求出最大值即可.
【详解】解:(1)∵抛物线的对称轴是x=1,
∴=1,∴a=1
由图像易知c=-3,所以抛物线解析式为, B(3,0),A(-1,0),C(0,-3)
设直线BC的函数表达式为:y=kx+b,
则,解得:k=1,b=-3,
∴直线BC的解析式为 ;
(2)如图,连结AM,
∵OB=OC,∴∠OCB=∠OBC=45°,
∴∠ADC =∠OBC=45°,∠AMC=90°,
又∵AM=CM,∴∠ACE=45°,
∴∠ACD =∠ECB=45°-∠ECD,
∴△ACD∽△ECB
(3)∵PQ∥y轴,∴△AOF∽△APQ,
∴.
∴,
∵PQ=,∴,
∴S=S△ADF+S△QDF=
整理得,
化为顶点式得S=﹣(t-)2+,∴当 .
【点睛】本题主要考查一次函数的图像与性质、二次函数的图像与性质、相似三角形的判定与性质、圆的相关性质,熟练掌握这些知识点并灵活运用,掌握数形结合的思想,是解答的关键.
24.(1)证明见解析;
(2)CF的长度是169cm.
【详解】试题分析:(1)利用“两角法”证得这两个三角形相似;
(2)由△BEF∽△CDF,根据相似三角形的对应边成比例来求线段CF的长度.
试题解析:(1)在矩形ABCD中,由对称性可得出:∠DFC=∠EFB,∠EBF=∠FCD=90°,
∴△BEF∽△CDF;
(2)∵△BEF∽△CDF.
∴,即,
解得:CF=169.
即:CF的长度是169cm.
考点:相似三角形的应用.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
