8.3统计分析帮你做预测同步练习(含解析)
文档属性
| 名称 | 8.3统计分析帮你做预测同步练习(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 691.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
8.3统计分析帮你做预测
学校:___________姓名:___________班级:___________考号:___________
一、单选题
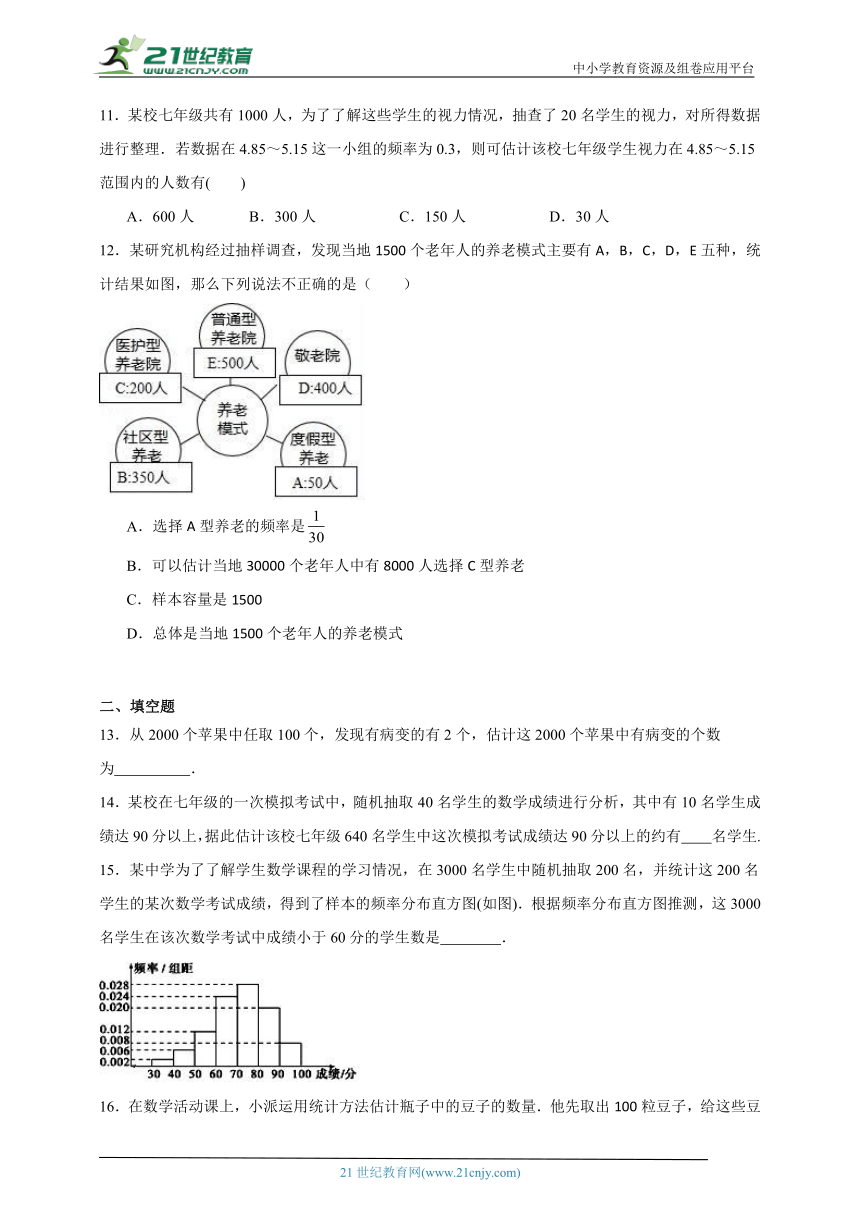
1.某校对学生“一周课外阅读时间”的情况进行随机抽样调查,调查结果如统计图所示.若该校有2000名学生,则根据调查结果可估算该校学生一周阅读时间不足3小时的人数是( )
A.280人 B.400人 C.660人 D.680人
2.由于各地雾霾天气越来越严重,2018年春节前夕,安庆市政府号召市民,禁放烟花炮竹.学校向3000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:使用电子鞭炮;D类:不会减少烟花爆竹数量”四个选项进行问卷调查(单选),并将对100名学生的调查结果绘制成统计图(如图所示).根据抽样结果,请估计全校“使用电子鞭炮”的学生有( )
A.900名 B.1050名 C.600名 D.450名
3.为了估计池塘里有多少条鱼,从池塘里捕捞了1000条鱼做上标记,然后放回池塘里,经过一段时间,等有标记的鱼完全混合于鱼群中以后,再捕捞200条,若其中有标记的鱼有5条,则估计池塘里有鱼( )
A.5000条 B.10000条 C.20000条 D.40000条
4.鱼塘中同时放养了300尾草鱼,从中捕获了10尾,称得每尾的质量分别为1.5,1.6,1.4,1.3,1.6,1.5,1.4,1.2,1.7,1.8(单位:千克),则可以估计这300尾草鱼的总质量约为( )
A.390千克 B.420千克 C.450千克 D.480千克
5.对泰顺某种学生快餐营养成分进行检测,绘制成如图所示统计图,已知快餐中碳水化合物有120克,那么快餐中脂肪有( )克
A.300 B.120 C.30 D.135
6.凤江镇有10万人口,随机调查了1000人,其中有20人喜欢看晚间新闻联播,则该镇中喜欢看晚间新闻联播的人数大约有( )人.
A.1000 B.2000 C.3000 D.4000
7.为了鼓励学生加强体育锻炼,学校在制定奖励方案前进行问卷调查,设置“赞成、反对、无所谓”三种意见,从全校2000名学生中随机抽取100名学生进行调查,其中持“反对”和“无所谓”意见的共有30名学生,估计全校持“赞成”意见的学生人数约为( )
A.600 B.800 C.1400 D.1680
8.生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉只雀鸟,给它们做上标记后放回山林;一段时间后,再从中随机捕捉只,其中有标记的雀鸟有只.请你帮助工作人员估计这片山林中雀鸟的数量约为( )
A.只 B.只 C.只 D.只
9.某地区家庭的年消费情况如下:年消费 10万元的有2 户,年消费 5万元的有1 户,年消费 1.5万元的有6户,年消费 7 千元的有1 户,可估计该地区每户年消费金额的一般水平为( )
A.1.5万元 B.5万元 C.10万元 D.3.47万元
10.某商场6月份随即调查了6天的营业额,结果分别如下(单位:万元):2.8,3.2,3.4,3.0,3.1,3.7,试估算该商场6月份总营业额大约是( )
A.84万元 B.96万元
C.93万元 D.111万元
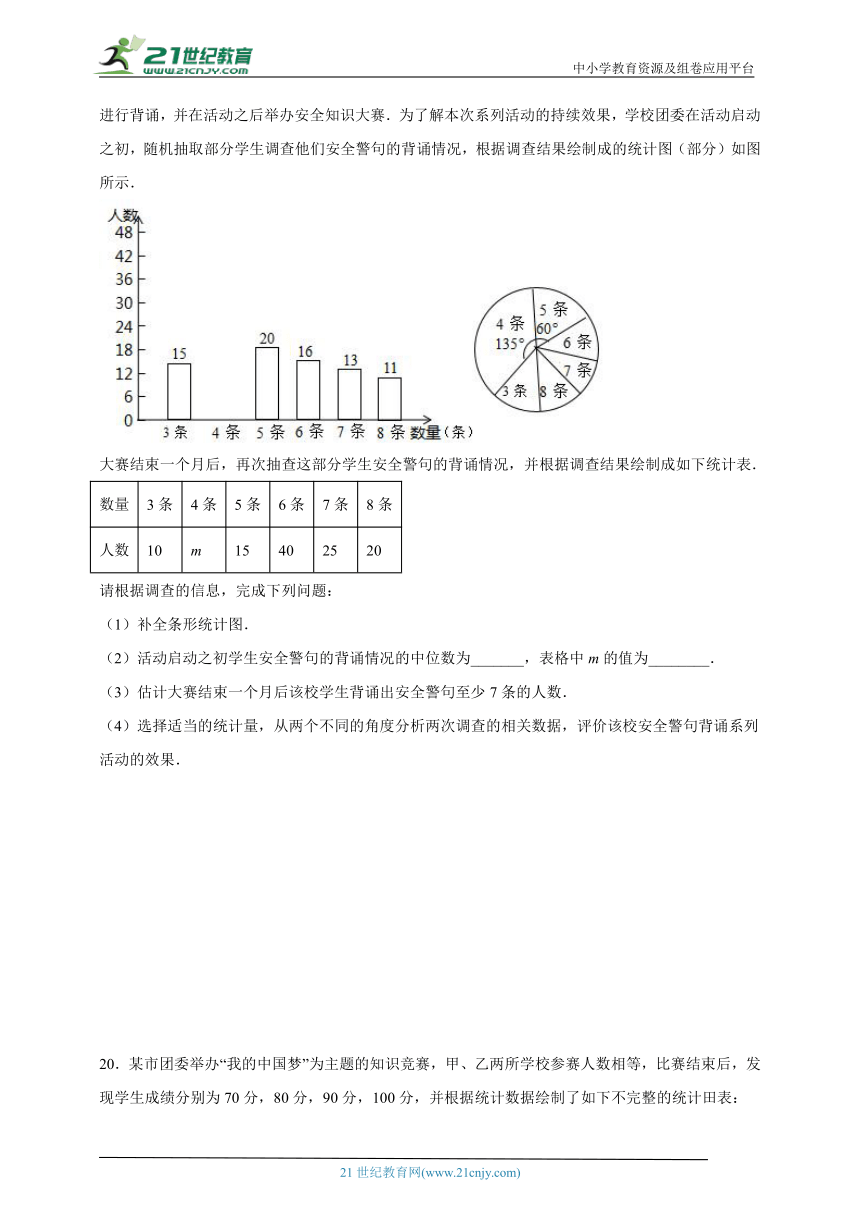
11.某校七年级共有1000人,为了了解这些学生的视力情况,抽查了20名学生的视力,对所得数据进行整理.若数据在4.85~5.15这一小组的频率为0.3,则可估计该校七年级学生视力在4.85~5.15范围内的人数有( )
A.600人 B.300人 C.150人 D.30人
12.某研究机构经过抽样调查,发现当地1500个老年人的养老模式主要有A,B,C,D,E五种,统计结果如图,那么下列说法不正确的是( )
A.选择A型养老的频率是
B.可以估计当地30000个老年人中有8000人选择C型养老
C.样本容量是1500
D.总体是当地1500个老年人的养老模式
二、填空题
13.从2000个苹果中任取100个,发现有病变的有2个,估计这2000个苹果中有病变的个数为 .
14.某校在七年级的一次模拟考试中,随机抽取40名学生的数学成绩进行分析,其中有10名学生成绩达90分以上,据此估计该校七年级640名学生中这次模拟考试成绩达90分以上的约有 名学生.
15.某中学为了了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是 .
16.在数学活动课上,小派运用统计方法估计瓶子中的豆子的数量.他先取出100粒豆子,给这些豆子做上记号,然后放回瓶子中,充分摇匀之后再取出100粒豆子,发现其中8粒有刚才做的记号,利用得到的数据可以估计瓶子中豆子的数量约为 粒.
17.李师傅随机抽查了本单位今年四月份里天的日用水量(单位:吨)结果如下:,,,,,,根据这些数据,估计四月份本单位用水总量为 吨.
三、解答题
18.在精准脱贫期间,江口县委、政府对江口教育制定了目标,为了保证2018年中考目标的实现,对九年级进行了一次模拟测试,现对这次模拟测试的数学成绩进行了分段统计,统计如表,共有2500名学生参加了这次模拟测试,为了解本次考试成绩,从中随机抽取了部分学生的数学成绩x(得分均为整数,满分为100分)进行统计后得到下表,请根据表格解答下列问题:
(1)随机抽取了多少学生?
(2)根据表格计算:a= ;b= .
分组 频数 频率
x<30 14 0.07
30≤x<60 32 b
60≤x<90 a 0.62
90≤x 30 0.15
合计 ﹣ 1
(3)设60分(含60)以上为合格,请据此估计我县这次这次九年级数学模拟测试成绩合格的学生有多少名?
19.为了提高学生的安全意识,珍爱生命,某学校制作了8条安全出行警句,倡导全校1200名学生进行背诵,并在活动之后举办安全知识大赛.为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查他们安全警句的背诵情况,根据调查结果绘制成的统计图(部分)如图所示.
大赛结束一个月后,再次抽查这部分学生安全警句的背诵情况,并根据调查结果绘制成如下统计表.
数量 3条 4条 5条 6条 7条 8条
人数 10 m 15 40 25 20
请根据调查的信息,完成下列问题:
(1)补全条形统计图.
(2)活动启动之初学生安全警句的背诵情况的中位数为_______,表格中m的值为________.
(3)估计大赛结束一个月后该校学生背诵出安全警句至少7条的人数.
(4)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校安全警句背诵系列活动的效果.
20.某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计田表:
乙校成绩统计表
分数(分) 人数(人)
70 7
80 a
90 1
100 8
(1)请你将图②条形图补充完整,并求出a的值;
(2)求甲、乙两校成绩的平均分;
(3)经计算知,,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
21.某市举行“建国70周年”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如下不完整的两幅统计图表.
请根指以上信息,解答下列问题
(1)征文比赛成绩频数分布表中,a= ,b= ,c= .
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
22.为挑选优秀同学参加云南省级英语听说能力竞赛,某中学举行了“英语单词听写”竞赛,每位学生听写单词99个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
根据以上信息解决下列问题:
(1)本次共随机抽查了 名学生,并补全频数分布直方图;
(2)若把每组听写正确的个数用这组数据的组中值代替,则被抽查学生听写正确的个数的平均数是多少?
(3)该校共有3000名学生,如果听写正确的个数少于60个定为不合格,请你估计这所学校本次竞赛听写不合格的学生人数.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D D D C C B C B D B
题号 11 12
答案 B B
1.D
【分析】由总人数乘以时间不足3小时的人数所占的比例即可.
【详解】解:(人),
即估算该校学生一周阅读时间不足3小时的人数是680人,
故选:D.
【点睛】本题考查的是用样本估计总体,读懂统计图,从统计图中得到必要的信息是解决问题的关键.
2.D
【分析】用全校学生的人数乘以“使用电子鞭炮”的百分比即可求出答案.
【详解】解:100名学生中“使用电子鞭炮”的学生有人,“使用电子鞭炮”的百分比为:
全校“使用电子鞭炮”的学生有:人.
故选D.
【点睛】本题考查用样本估计总体,从条形统计图中得到“使用电子鞭炮”的学生人数是解题的关键.
3.D
【分析】捕捞200条,若其中有标记的鱼有5条,说明有标记的占到,而有标记的共有1000条,根据所占比例即可解答.
【详解】解:1000÷=40 000(条).
故选:D.
【点睛】统计的思想就是用样本的信息来估计总体的信息,本题体现了统计思想,考查了用样本估计总体.
4.C
【分析】首先根据已知条件求出任选10的尾鱼的平均质量,然后利用样本估计总体的思想即可求解.
【详解】根据题意得:
300×(1.5+1.6+1.4+1.3+1.6+1.5+1.4+1.2+1.7+1.8)=450(千克),
答:这300尾草鱼的总质量约为450千克;
故选:C.
【点睛】本题主要考查了利用样本估计总体的思想,首先求出任选10的尾鱼的平均质量,然后利用样本估计总体的思想即可解决问题.
5.C
【分析】根据条件可先算出快餐的总量,然后再用总量乘以脂肪的占比即可算出结果;
【详解】根据已知条件可得营养成分总量=克,
所以脂肪=克.
故答案选C.
【点睛】本题主要考查了扇形统计图的相关计算,根据已知量求出总量是本题的解题关键.
6.B
【详解】该镇中喜欢看晚间新闻联播的人数大约有:=2000,故选B.
7.C
【分析】用总人数乘以样本中持“赞成”意见的学生人数占把被调查人数的比例即可得.
【详解】解:估计全校持“赞成”意见的学生人数约为(人,
故选:.
【点睛】本题主要考查用样本估计总体,从一个总体得到一个包含大量数据的样本,我们很难从一个个数字中直接看出样本所包含的信息.这时,我们用频率分布直方图来表示相应样本的频率分布,从而去估计总体的分布情况.
8.B
【分析】由题意可知:重新捕获500只,其中带标记的有5只,可以知道,在样本中,有标记的占到 .而在总体中,有标记的共有100只,根据比例即可解答.
【详解】解:100÷=10000只.
故选B.
【点睛】本题考查了用样本估计总体的知识,体现了统计思想,统计的思想就是用样本的信息来估计总体的信息.
9.D
【详解】试题解析:10户家庭的年消费的平均数为=3.47(万元).
故该地每户年消费金额的一般水平为3.47万元.
故选D.
点睛:用样本平均数来估计总体平均数.
10.B
【详解】该商场6月份的营业额可以用上面6天的营业额来估计,即算出随机抽查的6天的营业额的平均数(2.8+3.2+3.4+3.7+3.0+3.1)÷6=3.2,然后乘以6月份30天即可求得3.2×30=96(万元).
故选B.
点睛:本题考查了用样本的数据特征来估计总体的数据特征,利用样本中的数据对整体进行估算是统计学中最常用的估算方法,难度适中.
11.B
【详解】该校七年级学生视力在4.85 5.15范围内的人数=1000×0.3=300(人).
故选B.
12.B
【分析】根据频率定义、样本估计总体、样本容量和总体的概念逐一判断可得.
【详解】解:A、选择A型养老的频率是=,此选项说法正确;
B、可以估计当地30000个老年人中选择C型养老的人数为30000×=4000人,此选项说法错误;
C、样本容量是1500,此选项说法正确;
D、总体是当地1500个老年人的养老模式,此选项说法正确;
故选B.
【点睛】本题主要考查用样本估计总体,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,对总体的估计也就越精确.
13.40
【分析】首先可以求出样本的病变率,然后利用样本估计总体的思想即可求出这2000个苹果中有病变的个数.
【详解】解:∵从2000个苹果中任取100个,发现有病变的有2个,,
∴病变率为:2÷100=2%,
∴估计这2000个苹果中有病变的个数为2000×2%=40.
故答案为40.
【点睛】此题主要考查了利用样本估计总体的思想,解题时首先求出样本的病变率,然后利用样本估计总体的思想即可解决问题.
14.160
【详解】分析:先求出随机抽取的40名学生中成绩达到90分以上的所占的百分比,再乘以640,即可得出答案.
详解:∵随机抽取40名学生的数学成绩进行分析,有10名学生的成绩达90分以上,
∴七年级640名学生中这次模拟考数学成绩达90分以上的约有640×=160(名);
故答案为160.
点睛:此题主要考查了用样本估计总体,求出样本中符合条件的百分比是解题关键,比较简单.
15.600人
【分析】根据频率分布直方图,求出在该次数学考试中成绩小于60分的频率,再求成绩小于60分的学生数.
【详解】根据频率分布直方图,得
在该次数学考试中成绩小于60分的频率是
(0.002+0.006+0.012)×10=0.20
∴在该次数学考试中成绩小于60分的学生数是
3000×0.20=600.
故答案为600.
【点睛】本题考查了频率分布直方图的应用问题,解题时应根据频率分布直方图提供的数据,求出频率,再求出学生数,是基础题.
16.1250
【分析】设瓶子中有豆子x粒,根据取出100粒刚好有记号的8粒列出算式,计算即可.
【详解】设瓶子中有豆子x粒豆子,根据题意得:
,
解得:x=1250,
答:估计瓶子中豆子的数量约为1250粒.
故答案为:1250.
【点睛】本题考查了用样本估计总体的知识点,利用样本中的数据对整体进行估算是统计学中最常用的估算方法.
17.210
【分析】先求样本平均数,然后乘以30天即可.
【详解】吨.
故答案为:210.
【点睛】本题主要考查用样本估计总体的方法还可以根据已知数据有6天的用水量,求出总和然后乘以5即可.
18.(1)200名;(2)124,0.16;(3)1925名
【分析】(1)由题意根据频数分布表中的数据,可以计算出随机抽取的学生人数;
(2)由题意根据(1)中的数据和频数分布表中的数据,可以计算出a和b的值;
(3)根据频数分布表中的数据,即可计算出我县这次这次九年级数学模拟测试成绩合格的学生有多少名.
【详解】解:(1)14÷0.07=200(名),
即随机抽取了200名学生;
(2)a=200×0.62=124,b=32÷200=0.16,
故答案为:124,0.16;
(3)2500×(0.62+0.15)
=2500×0.77
=1925(名),
答:我县这次这次九年级数学模拟测试成绩合格的学生有1925名.
【点睛】本题考查频数分布表和用样本估计总体,解答本题的关键是明确题意并求出相应的数据.
19.(1)画图见解析;(2)4.5,10;(3)450;(4)分析见解析,活动效果好.
【分析】(1)根据题意可知背诵5条的学生占扇形统计图圆心角,结合条形统计图信息计算出抽查总人数,总人数减去其他已知人数就是背诵4条安全警句的人数;画出条形统计图即可.
(2)根据上一小题可知抽查总人数为120人,活动启动之初第60名同学背诵4条,第61名同学背诵5条,中位数为,表格中m的值为抽查总人数减去其他条数背诵人数,计算得出答案即可.
(3)用全校总人数乘活动后抽查背诵出安全警句至少7条的人数占抽查人数的比例,计算得出答案即可.
(4)可以从中位数、众数的角度计算、分析,从而得出结论.
【详解】解:(1)∵背诵5条安全警句的有20人,在扇形统计图中圆心角为,
∴抽查总人数为(人),
∴背诵4条安全警句的人数为:(人).
补全条形统计图,如图.
(2)根据上一小题可知抽查总人数为120人,活动之初按背诵条数由少到多排列,第60名同学背诵4条,第61名同学背诵5条,
∴活动启动之初学生安全警句的背诵情况的中位数为;
表格中m的值为:.
(3) 抽查学生背诵出安全警句至少7条的人数为:(人),
估计大赛结束一个月后该校学生背诵出安全警句至少7条的人数,
(人).
(4)大赛活动启动之初中位数为,众数为4条;
大赛活动启动之后中位数为6条,众数为6条.
从大赛活动前后抽查的中位数、众数来看,学生安全警句的背诵情况明显提高,活动效果好.
【点睛】本题考查了画条形统计图,求中位数、众数,由样本频数估计总体频数,从条形统计图和扇形统计图中关联数据信息,根据所学知识进行数据获取、分析并计算是解题关键.
20.(1)图形见解析,a=4;(2)甲、乙两校成绩的平均分都是85分;(3)甲校的成绩波动较小,甲校的成绩好于乙校的成绩
【分析】(1) 根据统计图可知甲班70分的有6人,从而可求得总人数,然后用总人数减去其他分数的人数即可得到100分的人数,利用两校的参赛人数相等求出a的值,补全图形即可;
(2)用加权平均数的计算公式求出两校的平均分;
(3)根据方差的意义即可做出评价.
【详解】(1)甲班总人数为:(人),
∴100分的人数为20-6-3-6=5(人),
∵甲、乙两所学校参赛人数相等,
∴a=20-7-1-8=4,
补全图形:
(2)甲校的平均分==85(分),
∴乙校的平均分==85(分),
(3)∵,,
∴S甲∴甲校的成绩波动较小,甲校的成绩好于乙校的成绩.
【点睛】本题考查的是条形统计图和扇形统计图,表格的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
21.(1)30,20,20%;(2)见解析;(3)300篇
【分析】(1)先用40÷40%求出抽取的数据总数,再用100乘以30%即可求出a的值,然后用数据总数减去其它三个组的数据即为b的值,最后用b的值除以数据总数即得c的值;
(2)根据(1)题中求出的a、b的值即可补全频数分布直方图;
(3)用后两个组的百分比的和乘以1000即得结果.
【详解】解:(1)40÷40%=100,
∴a=100×30%=30,b=100-40-30-10=20,c=20÷100=20%;
故答案为:30,20,20%;
(2)补全频数分布直方图如图所示:
(3)1000×(20%+10%)=300(篇),
答:估计全市获得一等奖征文的篇数为300篇.
【点睛】本题考查了频数分布表和频数分布直方图以及利用样本估计总体的思想,属于常考题型,熟练掌握频数分布表和频数分布直方图的相关知识是解题关键.
22.(1)100,见解析;(2)57个;(3)1500人
【分析】(1)根据A组的人数和对应的百分比即可求出答案,再补全频数分布直方图即可;
(2)根据平均数的计算方法计算即可;
(3)用总人数乘以不合格人数所占的百分比即可.
【详解】解:(1)解:10÷10%=100(人),
答:本次共随机抽查了100名学生;
D组人数:100×30%=30(人),
100-10-15-25-30=20(人),
补全的频数分布直方图如下:
(2)=(10×10+15×30+25×50+30×70+90×20)=57(个),
答:被抽查学生听写正确的个数的平均数是57个;
(3)3000×(10%+15%+25%)=1500(人),
答:估计这所学校本次竞赛听写不合格的学生人数为1500人.
【点睛】本题考查了平均数,扇形统计图,用样本估计总体,从表中获取所需数据是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
8.3统计分析帮你做预测
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.某校对学生“一周课外阅读时间”的情况进行随机抽样调查,调查结果如统计图所示.若该校有2000名学生,则根据调查结果可估算该校学生一周阅读时间不足3小时的人数是( )
A.280人 B.400人 C.660人 D.680人
2.由于各地雾霾天气越来越严重,2018年春节前夕,安庆市政府号召市民,禁放烟花炮竹.学校向3000名学生发出“减少空气污染,少放烟花爆竹”倡议书,并围绕“A类:不放烟花爆竹;B类:少放烟花爆竹;C类:使用电子鞭炮;D类:不会减少烟花爆竹数量”四个选项进行问卷调查(单选),并将对100名学生的调查结果绘制成统计图(如图所示).根据抽样结果,请估计全校“使用电子鞭炮”的学生有( )
A.900名 B.1050名 C.600名 D.450名
3.为了估计池塘里有多少条鱼,从池塘里捕捞了1000条鱼做上标记,然后放回池塘里,经过一段时间,等有标记的鱼完全混合于鱼群中以后,再捕捞200条,若其中有标记的鱼有5条,则估计池塘里有鱼( )
A.5000条 B.10000条 C.20000条 D.40000条
4.鱼塘中同时放养了300尾草鱼,从中捕获了10尾,称得每尾的质量分别为1.5,1.6,1.4,1.3,1.6,1.5,1.4,1.2,1.7,1.8(单位:千克),则可以估计这300尾草鱼的总质量约为( )
A.390千克 B.420千克 C.450千克 D.480千克
5.对泰顺某种学生快餐营养成分进行检测,绘制成如图所示统计图,已知快餐中碳水化合物有120克,那么快餐中脂肪有( )克
A.300 B.120 C.30 D.135
6.凤江镇有10万人口,随机调查了1000人,其中有20人喜欢看晚间新闻联播,则该镇中喜欢看晚间新闻联播的人数大约有( )人.
A.1000 B.2000 C.3000 D.4000
7.为了鼓励学生加强体育锻炼,学校在制定奖励方案前进行问卷调查,设置“赞成、反对、无所谓”三种意见,从全校2000名学生中随机抽取100名学生进行调查,其中持“反对”和“无所谓”意见的共有30名学生,估计全校持“赞成”意见的学生人数约为( )
A.600 B.800 C.1400 D.1680
8.生物工作者为了估计一片山林中雀鸟的数量,设计了如下方案:先捕捉只雀鸟,给它们做上标记后放回山林;一段时间后,再从中随机捕捉只,其中有标记的雀鸟有只.请你帮助工作人员估计这片山林中雀鸟的数量约为( )
A.只 B.只 C.只 D.只
9.某地区家庭的年消费情况如下:年消费 10万元的有2 户,年消费 5万元的有1 户,年消费 1.5万元的有6户,年消费 7 千元的有1 户,可估计该地区每户年消费金额的一般水平为( )
A.1.5万元 B.5万元 C.10万元 D.3.47万元
10.某商场6月份随即调查了6天的营业额,结果分别如下(单位:万元):2.8,3.2,3.4,3.0,3.1,3.7,试估算该商场6月份总营业额大约是( )
A.84万元 B.96万元
C.93万元 D.111万元
11.某校七年级共有1000人,为了了解这些学生的视力情况,抽查了20名学生的视力,对所得数据进行整理.若数据在4.85~5.15这一小组的频率为0.3,则可估计该校七年级学生视力在4.85~5.15范围内的人数有( )
A.600人 B.300人 C.150人 D.30人
12.某研究机构经过抽样调查,发现当地1500个老年人的养老模式主要有A,B,C,D,E五种,统计结果如图,那么下列说法不正确的是( )
A.选择A型养老的频率是
B.可以估计当地30000个老年人中有8000人选择C型养老
C.样本容量是1500
D.总体是当地1500个老年人的养老模式
二、填空题
13.从2000个苹果中任取100个,发现有病变的有2个,估计这2000个苹果中有病变的个数为 .
14.某校在七年级的一次模拟考试中,随机抽取40名学生的数学成绩进行分析,其中有10名学生成绩达90分以上,据此估计该校七年级640名学生中这次模拟考试成绩达90分以上的约有 名学生.
15.某中学为了了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某次数学考试成绩,得到了样本的频率分布直方图(如图).根据频率分布直方图推测,这3000名学生在该次数学考试中成绩小于60分的学生数是 .
16.在数学活动课上,小派运用统计方法估计瓶子中的豆子的数量.他先取出100粒豆子,给这些豆子做上记号,然后放回瓶子中,充分摇匀之后再取出100粒豆子,发现其中8粒有刚才做的记号,利用得到的数据可以估计瓶子中豆子的数量约为 粒.
17.李师傅随机抽查了本单位今年四月份里天的日用水量(单位:吨)结果如下:,,,,,,根据这些数据,估计四月份本单位用水总量为 吨.
三、解答题
18.在精准脱贫期间,江口县委、政府对江口教育制定了目标,为了保证2018年中考目标的实现,对九年级进行了一次模拟测试,现对这次模拟测试的数学成绩进行了分段统计,统计如表,共有2500名学生参加了这次模拟测试,为了解本次考试成绩,从中随机抽取了部分学生的数学成绩x(得分均为整数,满分为100分)进行统计后得到下表,请根据表格解答下列问题:
(1)随机抽取了多少学生?
(2)根据表格计算:a= ;b= .
分组 频数 频率
x<30 14 0.07
30≤x<60 32 b
60≤x<90 a 0.62
90≤x 30 0.15
合计 ﹣ 1
(3)设60分(含60)以上为合格,请据此估计我县这次这次九年级数学模拟测试成绩合格的学生有多少名?
19.为了提高学生的安全意识,珍爱生命,某学校制作了8条安全出行警句,倡导全校1200名学生进行背诵,并在活动之后举办安全知识大赛.为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取部分学生调查他们安全警句的背诵情况,根据调查结果绘制成的统计图(部分)如图所示.
大赛结束一个月后,再次抽查这部分学生安全警句的背诵情况,并根据调查结果绘制成如下统计表.
数量 3条 4条 5条 6条 7条 8条
人数 10 m 15 40 25 20
请根据调查的信息,完成下列问题:
(1)补全条形统计图.
(2)活动启动之初学生安全警句的背诵情况的中位数为_______,表格中m的值为________.
(3)估计大赛结束一个月后该校学生背诵出安全警句至少7条的人数.
(4)选择适当的统计量,从两个不同的角度分析两次调查的相关数据,评价该校安全警句背诵系列活动的效果.
20.某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分,80分,90分,100分,并根据统计数据绘制了如下不完整的统计田表:
乙校成绩统计表
分数(分) 人数(人)
70 7
80 a
90 1
100 8
(1)请你将图②条形图补充完整,并求出a的值;
(2)求甲、乙两校成绩的平均分;
(3)经计算知,,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
21.某市举行“建国70周年”征文比赛,已知每篇参赛征文成绩记m分(60≤m≤100),组委会从1000篇征文随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如下不完整的两幅统计图表.
请根指以上信息,解答下列问题
(1)征文比赛成绩频数分布表中,a= ,b= ,c= .
(2)补全征文比赛成绩频数分布直方图;
(3)若80分以上(含80分)的征文将被评为一等奖,试估计全市获得一等奖征文的篇数.
22.为挑选优秀同学参加云南省级英语听说能力竞赛,某中学举行了“英语单词听写”竞赛,每位学生听写单词99个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
根据以上信息解决下列问题:
(1)本次共随机抽查了 名学生,并补全频数分布直方图;
(2)若把每组听写正确的个数用这组数据的组中值代替,则被抽查学生听写正确的个数的平均数是多少?
(3)该校共有3000名学生,如果听写正确的个数少于60个定为不合格,请你估计这所学校本次竞赛听写不合格的学生人数.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 D D D C C B C B D B
题号 11 12
答案 B B
1.D
【分析】由总人数乘以时间不足3小时的人数所占的比例即可.
【详解】解:(人),
即估算该校学生一周阅读时间不足3小时的人数是680人,
故选:D.
【点睛】本题考查的是用样本估计总体,读懂统计图,从统计图中得到必要的信息是解决问题的关键.
2.D
【分析】用全校学生的人数乘以“使用电子鞭炮”的百分比即可求出答案.
【详解】解:100名学生中“使用电子鞭炮”的学生有人,“使用电子鞭炮”的百分比为:
全校“使用电子鞭炮”的学生有:人.
故选D.
【点睛】本题考查用样本估计总体,从条形统计图中得到“使用电子鞭炮”的学生人数是解题的关键.
3.D
【分析】捕捞200条,若其中有标记的鱼有5条,说明有标记的占到,而有标记的共有1000条,根据所占比例即可解答.
【详解】解:1000÷=40 000(条).
故选:D.
【点睛】统计的思想就是用样本的信息来估计总体的信息,本题体现了统计思想,考查了用样本估计总体.
4.C
【分析】首先根据已知条件求出任选10的尾鱼的平均质量,然后利用样本估计总体的思想即可求解.
【详解】根据题意得:
300×(1.5+1.6+1.4+1.3+1.6+1.5+1.4+1.2+1.7+1.8)=450(千克),
答:这300尾草鱼的总质量约为450千克;
故选:C.
【点睛】本题主要考查了利用样本估计总体的思想,首先求出任选10的尾鱼的平均质量,然后利用样本估计总体的思想即可解决问题.
5.C
【分析】根据条件可先算出快餐的总量,然后再用总量乘以脂肪的占比即可算出结果;
【详解】根据已知条件可得营养成分总量=克,
所以脂肪=克.
故答案选C.
【点睛】本题主要考查了扇形统计图的相关计算,根据已知量求出总量是本题的解题关键.
6.B
【详解】该镇中喜欢看晚间新闻联播的人数大约有:=2000,故选B.
7.C
【分析】用总人数乘以样本中持“赞成”意见的学生人数占把被调查人数的比例即可得.
【详解】解:估计全校持“赞成”意见的学生人数约为(人,
故选:.
【点睛】本题主要考查用样本估计总体,从一个总体得到一个包含大量数据的样本,我们很难从一个个数字中直接看出样本所包含的信息.这时,我们用频率分布直方图来表示相应样本的频率分布,从而去估计总体的分布情况.
8.B
【分析】由题意可知:重新捕获500只,其中带标记的有5只,可以知道,在样本中,有标记的占到 .而在总体中,有标记的共有100只,根据比例即可解答.
【详解】解:100÷=10000只.
故选B.
【点睛】本题考查了用样本估计总体的知识,体现了统计思想,统计的思想就是用样本的信息来估计总体的信息.
9.D
【详解】试题解析:10户家庭的年消费的平均数为=3.47(万元).
故该地每户年消费金额的一般水平为3.47万元.
故选D.
点睛:用样本平均数来估计总体平均数.
10.B
【详解】该商场6月份的营业额可以用上面6天的营业额来估计,即算出随机抽查的6天的营业额的平均数(2.8+3.2+3.4+3.7+3.0+3.1)÷6=3.2,然后乘以6月份30天即可求得3.2×30=96(万元).
故选B.
点睛:本题考查了用样本的数据特征来估计总体的数据特征,利用样本中的数据对整体进行估算是统计学中最常用的估算方法,难度适中.
11.B
【详解】该校七年级学生视力在4.85 5.15范围内的人数=1000×0.3=300(人).
故选B.
12.B
【分析】根据频率定义、样本估计总体、样本容量和总体的概念逐一判断可得.
【详解】解:A、选择A型养老的频率是=,此选项说法正确;
B、可以估计当地30000个老年人中选择C型养老的人数为30000×=4000人,此选项说法错误;
C、样本容量是1500,此选项说法正确;
D、总体是当地1500个老年人的养老模式,此选项说法正确;
故选B.
【点睛】本题主要考查用样本估计总体,一般来说,用样本去估计总体时,样本越具有代表性、容量越大,对总体的估计也就越精确.
13.40
【分析】首先可以求出样本的病变率,然后利用样本估计总体的思想即可求出这2000个苹果中有病变的个数.
【详解】解:∵从2000个苹果中任取100个,发现有病变的有2个,,
∴病变率为:2÷100=2%,
∴估计这2000个苹果中有病变的个数为2000×2%=40.
故答案为40.
【点睛】此题主要考查了利用样本估计总体的思想,解题时首先求出样本的病变率,然后利用样本估计总体的思想即可解决问题.
14.160
【详解】分析:先求出随机抽取的40名学生中成绩达到90分以上的所占的百分比,再乘以640,即可得出答案.
详解:∵随机抽取40名学生的数学成绩进行分析,有10名学生的成绩达90分以上,
∴七年级640名学生中这次模拟考数学成绩达90分以上的约有640×=160(名);
故答案为160.
点睛:此题主要考查了用样本估计总体,求出样本中符合条件的百分比是解题关键,比较简单.
15.600人
【分析】根据频率分布直方图,求出在该次数学考试中成绩小于60分的频率,再求成绩小于60分的学生数.
【详解】根据频率分布直方图,得
在该次数学考试中成绩小于60分的频率是
(0.002+0.006+0.012)×10=0.20
∴在该次数学考试中成绩小于60分的学生数是
3000×0.20=600.
故答案为600.
【点睛】本题考查了频率分布直方图的应用问题,解题时应根据频率分布直方图提供的数据,求出频率,再求出学生数,是基础题.
16.1250
【分析】设瓶子中有豆子x粒,根据取出100粒刚好有记号的8粒列出算式,计算即可.
【详解】设瓶子中有豆子x粒豆子,根据题意得:
,
解得:x=1250,
答:估计瓶子中豆子的数量约为1250粒.
故答案为:1250.
【点睛】本题考查了用样本估计总体的知识点,利用样本中的数据对整体进行估算是统计学中最常用的估算方法.
17.210
【分析】先求样本平均数,然后乘以30天即可.
【详解】吨.
故答案为:210.
【点睛】本题主要考查用样本估计总体的方法还可以根据已知数据有6天的用水量,求出总和然后乘以5即可.
18.(1)200名;(2)124,0.16;(3)1925名
【分析】(1)由题意根据频数分布表中的数据,可以计算出随机抽取的学生人数;
(2)由题意根据(1)中的数据和频数分布表中的数据,可以计算出a和b的值;
(3)根据频数分布表中的数据,即可计算出我县这次这次九年级数学模拟测试成绩合格的学生有多少名.
【详解】解:(1)14÷0.07=200(名),
即随机抽取了200名学生;
(2)a=200×0.62=124,b=32÷200=0.16,
故答案为:124,0.16;
(3)2500×(0.62+0.15)
=2500×0.77
=1925(名),
答:我县这次这次九年级数学模拟测试成绩合格的学生有1925名.
【点睛】本题考查频数分布表和用样本估计总体,解答本题的关键是明确题意并求出相应的数据.
19.(1)画图见解析;(2)4.5,10;(3)450;(4)分析见解析,活动效果好.
【分析】(1)根据题意可知背诵5条的学生占扇形统计图圆心角,结合条形统计图信息计算出抽查总人数,总人数减去其他已知人数就是背诵4条安全警句的人数;画出条形统计图即可.
(2)根据上一小题可知抽查总人数为120人,活动启动之初第60名同学背诵4条,第61名同学背诵5条,中位数为,表格中m的值为抽查总人数减去其他条数背诵人数,计算得出答案即可.
(3)用全校总人数乘活动后抽查背诵出安全警句至少7条的人数占抽查人数的比例,计算得出答案即可.
(4)可以从中位数、众数的角度计算、分析,从而得出结论.
【详解】解:(1)∵背诵5条安全警句的有20人,在扇形统计图中圆心角为,
∴抽查总人数为(人),
∴背诵4条安全警句的人数为:(人).
补全条形统计图,如图.
(2)根据上一小题可知抽查总人数为120人,活动之初按背诵条数由少到多排列,第60名同学背诵4条,第61名同学背诵5条,
∴活动启动之初学生安全警句的背诵情况的中位数为;
表格中m的值为:.
(3) 抽查学生背诵出安全警句至少7条的人数为:(人),
估计大赛结束一个月后该校学生背诵出安全警句至少7条的人数,
(人).
(4)大赛活动启动之初中位数为,众数为4条;
大赛活动启动之后中位数为6条,众数为6条.
从大赛活动前后抽查的中位数、众数来看,学生安全警句的背诵情况明显提高,活动效果好.
【点睛】本题考查了画条形统计图,求中位数、众数,由样本频数估计总体频数,从条形统计图和扇形统计图中关联数据信息,根据所学知识进行数据获取、分析并计算是解题关键.
20.(1)图形见解析,a=4;(2)甲、乙两校成绩的平均分都是85分;(3)甲校的成绩波动较小,甲校的成绩好于乙校的成绩
【分析】(1) 根据统计图可知甲班70分的有6人,从而可求得总人数,然后用总人数减去其他分数的人数即可得到100分的人数,利用两校的参赛人数相等求出a的值,补全图形即可;
(2)用加权平均数的计算公式求出两校的平均分;
(3)根据方差的意义即可做出评价.
【详解】(1)甲班总人数为:(人),
∴100分的人数为20-6-3-6=5(人),
∵甲、乙两所学校参赛人数相等,
∴a=20-7-1-8=4,
补全图形:
(2)甲校的平均分==85(分),
∴乙校的平均分==85(分),
(3)∵,,
∴S甲
【点睛】本题考查的是条形统计图和扇形统计图,表格的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键,条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
21.(1)30,20,20%;(2)见解析;(3)300篇
【分析】(1)先用40÷40%求出抽取的数据总数,再用100乘以30%即可求出a的值,然后用数据总数减去其它三个组的数据即为b的值,最后用b的值除以数据总数即得c的值;
(2)根据(1)题中求出的a、b的值即可补全频数分布直方图;
(3)用后两个组的百分比的和乘以1000即得结果.
【详解】解:(1)40÷40%=100,
∴a=100×30%=30,b=100-40-30-10=20,c=20÷100=20%;
故答案为:30,20,20%;
(2)补全频数分布直方图如图所示:
(3)1000×(20%+10%)=300(篇),
答:估计全市获得一等奖征文的篇数为300篇.
【点睛】本题考查了频数分布表和频数分布直方图以及利用样本估计总体的思想,属于常考题型,熟练掌握频数分布表和频数分布直方图的相关知识是解题关键.
22.(1)100,见解析;(2)57个;(3)1500人
【分析】(1)根据A组的人数和对应的百分比即可求出答案,再补全频数分布直方图即可;
(2)根据平均数的计算方法计算即可;
(3)用总人数乘以不合格人数所占的百分比即可.
【详解】解:(1)解:10÷10%=100(人),
答:本次共随机抽查了100名学生;
D组人数:100×30%=30(人),
100-10-15-25-30=20(人),
补全的频数分布直方图如下:
(2)=(10×10+15×30+25×50+30×70+90×20)=57(个),
答:被抽查学生听写正确的个数的平均数是57个;
(3)3000×(10%+15%+25%)=1500(人),
答:估计这所学校本次竞赛听写不合格的学生人数为1500人.
【点睛】本题考查了平均数,扇形统计图,用样本估计总体,从表中获取所需数据是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
