第七章锐角三角函数同步练习（含解析）

中小学教育资源及组卷应用平台
第七章锐角三角函数
学校:___________姓名：___________班级：___________考号：___________
一、单选题
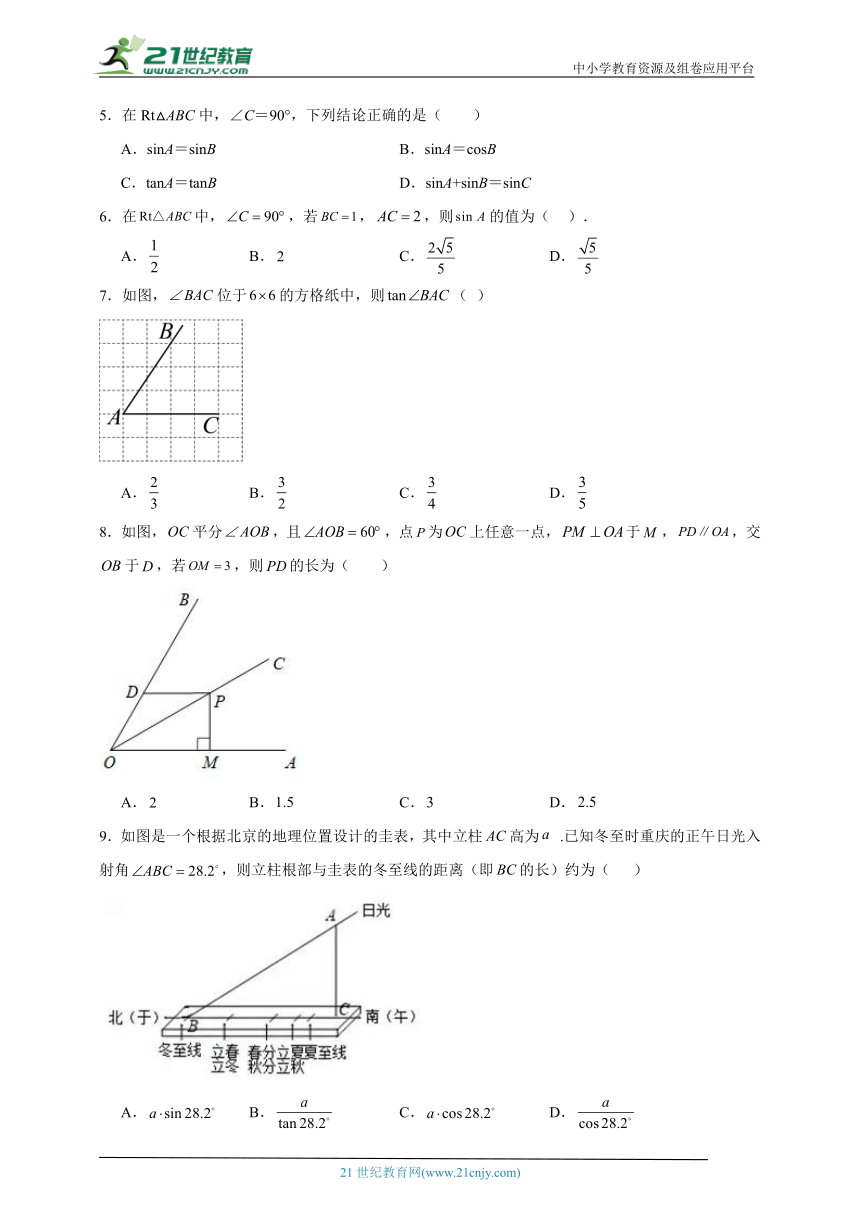
1．如图，将的一直角边与刻度尺的边缘重合，点对应的刻度分别为1和6，若，则的斜边的长为（ ）
A． B． C．5 D．
2．如图，在Rt△ABC中，∠ABC=90°，tan∠BAC=4，A（0，a），B（b，0），点C在第四象限，BC与y轴交于点D（0，c），若y轴平分∠BAC，则点C的坐标不能表示为（　　）

A．（4a+b，4b） B．（2a+2c，﹣8c﹣8a）
C．（﹣b﹣4c，4b） D．（2a﹣2c，﹣8c﹣8a）
3．如图，在中，已知，，是的外心，是的中点，则（ ）
A． B． C． D．
4．在中，，，，则的值是( )
A． B． C． D．
5．在Rt△ABC中，∠C＝90°，下列结论正确的是（　　）
A．sinA＝sinB B．sinA＝cosB
C．tanA＝tanB D．sinA+sinB＝sinC
6．在中，，若，，则的值为（ ）．
A． B． C． D．
7．如图，位于的方格纸中，则（ ）

A． B． C． D．
8．如图，平分，且，点为上任意一点，于，，交于，若，则的长为（　　）
A． B． C． D．
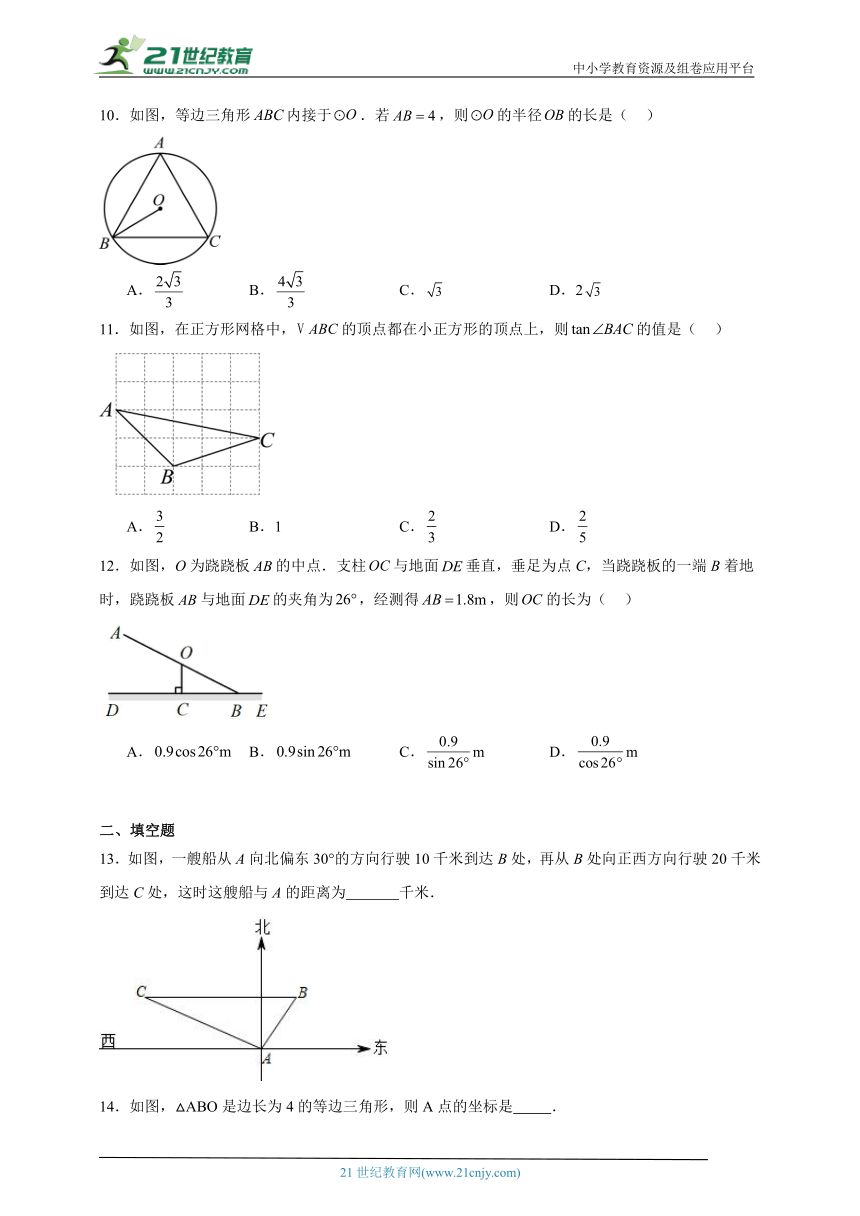
9．如图是一个根据北京的地理位置设计的圭表，其中立柱高为 .已知冬至时重庆的正午日光入射角，则立柱根部与圭表的冬至线的距离（即的长）约为（　 ）
A． B． C． D．
10．如图，等边三角形内接于．若，则的半径的长是（ ）
A． B． C． D．2
11．如图，在正方形网格中，的顶点都在小正方形的顶点上，则的值是（ ）
A． B．1 C． D．
12．如图，O为跷跷板的中点．支柱与地面垂直，垂足为点C，当跷跷板的一端B着地时，跷跷板与地面的夹角为，经测得，则的长为（ ）
A． B． C．m D．m
二、填空题
13．如图，一艘船从A向北偏东30°的方向行驶10千米到达B处，再从B处向正西方向行驶20千米到达C处，这时这艘船与A的距离为 千米．
14．如图，△ABO是边长为4的等边三角形，则A点的坐标是 ．
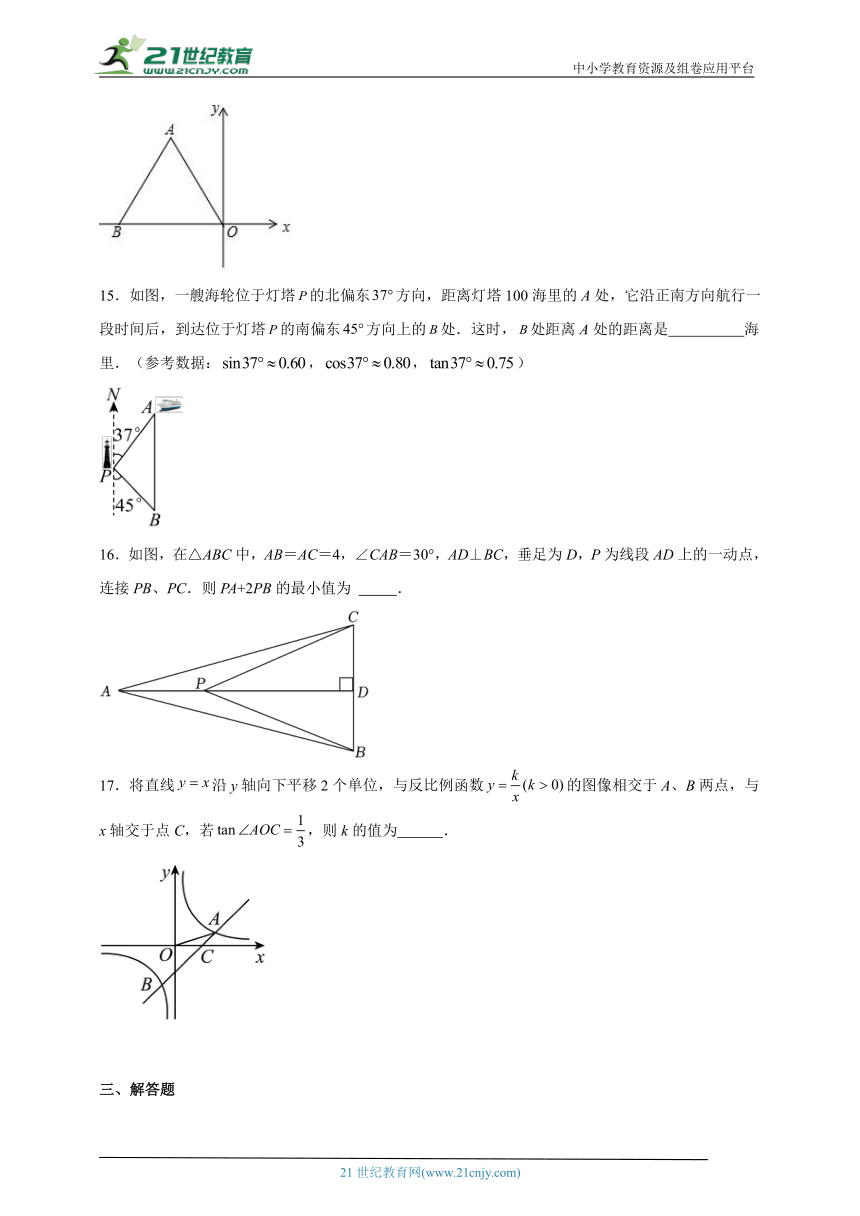
15．如图，一艘海轮位于灯塔的北偏东方向，距离灯塔100海里的A处，它沿正南方向航行一段时间后，到达位于灯塔的南偏东方向上的处．这时，处距离A处的距离是 海里．（参考数据：，，）
16．如图，在△ABC中，AB＝AC＝4，∠CAB＝30°，AD⊥BC，垂足为D，P为线段AD上的一动点，连接PB、PC．则PA+2PB的最小值为 ．
17．将直线沿y轴向下平移2个单位，与反比例函数的图像相交于A、B两点，与x轴交于点C，若，则k的值为 ．
三、解答题
18．计算：
19．如图，在下列14×7的网格中，横、纵坐标均为整点的数叫做格点，例如A(－6，0)、B(－3，4)都是格点．
（1）直接写出△ABO的形状；
（2）要求在下图中仅用无刻度的直尺作图：将△ABO绕点O顺时针旋转得△DEO，且点B的对应点E落在x轴正半轴上．操作如下：
第一步：在x正半轴上找一个格点E，使OE=OB；
第二步：找一个格点F，使∠EOF=∠AOB；
第三步：找一个格点M，作直线长AM交直线OF于D，连DE，则△DEO即为所作出的图形．
请你按步骤完成作图，并直接写出直线AM的解析式．
20．“天幕”是大家特别喜欢的一种露营设备，既起到遮阳防雨的作用，又开放通风．图1是一种“天幕”，图2是其截面示意图，其截面示意图为轴对称图形，，于点O，于点B，于点F，天晴时打开“天幕”遮阳，．
(1)求遮阳宽度的长；
(2)将拉绳固定在天幕杆上，若支杆与天幕杆的横向距离，求拉绳的长．
21．春暖花开，一组同学相约去放风筝，并利用所学知识测量风筝的高度．如图，在处用测角仪测得风筝的仰角为，保持风筝不动，沿方向前进到达处，又测得风筝的仰角为．已知测角仪的高度为．求风筝的高度(结果精确到米；参考数据：，，，，，)
22．如图，某测绘小组计划利用无人机测量某段山体的长度AB，无人机飞行速度为，无人机先是悬停在山体边缘A点正上方C处，然后沿山体的平行方向飞行18s到D处悬停，测得山体边缘A点的俯角为，然后继续向前飞行到达E处，测得山体边缘B点的俯角为．试求山体的长度．（参考数据：，，）
23．如图，在△ABC中，∠ABC的平分线BD交AC于点D，AE⊥BC于点E，已知∠ABC＝60°，∠C＝45°．
(1)求证：AB＝BD；
(2)若AE＝3，求△ABC的面积．
24．如图，是的直径，E是上一点，的平分线交于点C，过点C作交的延长线于点D．

(1)填空：______（选填“>”、“<”或“＝”）；
(2)求证：是的切线；
(3)若，求阴影部分的面积．
参考答案：
题号 1 2 3 4 5 6 7 8 9 10
答案 A B C B B D B A B B
题号 11 12
答案 C B
1．A
【分析】此题考查了解直角三角形，勾股定理，首先根据求出，然后利用勾股定理求解即可．
【详解】∵点对应的刻度分别为1和6，
∴
∵
∴
解得
∵
∴．
故选：A．
2．B
【分析】作CH⊥x轴于H，AC交OH于F．证明△ABO≌△AFO（ASA），则OB=OF，由△CBH∽△BAO，推出=4，推出BH=4a，CH=﹣4b，推出C（b+4a，4b），由题意可证△CHF∽△BOD，可得=，推出，推出FH=﹣4c，可得C（﹣b﹣4c，4b），因为﹣b﹣4c = b+4a，推出b=﹣2a﹣2c，可得C（2a﹣2c，﹣8a﹣8c），由此即可判断；
【详解】作CH⊥x轴于H，AC交OH于F．

∵y轴平分∠BAC，
∴∠BAO=∠FAO，
∵∠ABO=∠AOF=90°，AO=AO，
∴△ABO≌△AFO（ASA），
∴OB=OF，
∵∠CBH+∠ABH=90°，∠ABH+∠OAB=90°，
∴∠CBH=∠BAO，
∵∠CHB=∠AOB=90°，
∴Rt△CBH∽Rt△BAO，
∴，
∵tan∠BAC==4，A（0，a），B（b，0），
∴BO=-b，AO=a，
∴，
∴BH=4a，CH=﹣4b，
∴C（b+4a，4b），
∵△ABO≌△AFO，
∴∠ABO=∠AFO=∠CFH，
∵∠DBO+∠ABO=90°，∠DBO +∠BDO=90°，
∴∠ABO=∠BDO，
∴∠BDO=∠CFH，
∴Rt△CHF∽Rt△BOD，
∴，
∴，
∴FH=﹣4c，
∴C（﹣b﹣4c，4b），
∵C（b+4a，4b），
∴﹣b﹣4c = b+4a，
∴b=﹣2a﹣2c，
∴C（2a﹣2c，﹣8a﹣8c），
故选：B．
【点睛】本题考查了锐角三角函数、坐标与图形的性质、全等三角形的判定与性质、相似三角形的判定和性质等知识，解题的关键是正确寻找相似三角形解决问题．
3．C
【分析】本题考查了三角形的外接圆，解直角三角形，勾股定理，圆周角定理，连接，，以点为圆心，以为半径作的外接圆，根据三角形外接圆的圆心是三角形三条边垂直平分线的交点可得，，结合等腰三角形底边上的中线与顶角的角平分线重合可得，根据锐角三角函数可求得，最后由勾股定理即可求解，熟练掌握知识点的应用是解题的关键．
【详解】解：连接，，以点为圆心，以为半径作的外接圆，如图所示：
∵是的外心，是的中点，，
∴，，，
∵，
∴，
故，
在中，，
∴，
∴，
由勾股定理得：，
即，
解得：（负值舍去）；
故答案为：．
4．B
【分析】本题考查锐角三角函数的定义及运用，利用正弦的定义求解即可．
【详解】解：∵，，，
∴．
故选：B．
5．B
【分析】根据互余两角三角函数的关系直接作答．
【详解】A、当∠A＝∠B时，该等式成立，故本选项不符合题意．
B、由于∠A＝90°﹣∠B，所以sinA＝cosB，故本选项符合题意．
C、当∠A＝∠B时，tanA＝tanB，故本选项不符合题意．
D、sinA+sinB≠sinC，故本选项不符合题意．
故选：B．
【点睛】此题考查锐角三角函数，根据角度互余确定两角的三角函数值.
6．D
【分析】首先利用勾股定理求得AB的长度，然后利用三角函数的定义求解．
【详解】在中，，若，，
∴，
∴，
故选．
【点睛】此题考查锐角三角函数的定义，勾股定理，解题关键在于掌握各性质定理
7．B
【分析】由于B是边上的一点，D是上一点，于是正好构成直角三角形，再根据锐角三角函数的定义求解即可．
【详解】解:如图所示，

由于、均为上的点，根据网格的特点可知正好构成直角三角形，
设网格的边长为1，
则，，
于是．
故选：B．
【点睛】本题考查的是锐角三角函数的定义，解答此类问题的关键是在角的两边上找准两点，使三角形构成直角三角形，再根据锐角三角函数的定义解答．
8．A
【分析】过点作于点，根据角平分线的定义可得到，再根据平行线的性质和角平分线的性质得到的长度，进而利用特殊角的三角函数值即可得到的长度．
【详解】解：过点作于点，
∵平分，且，
∴，，
∵于，，
∴在中，，
∵，
∴，
∴，
∴在中，，
故选．
【点睛】本题考查了角平分线的性质，角平分线的定义，解直角三角形，平行线的性质，掌握角平分线的性质是解题的关键．
9．B
【分析】根据题意和图形，通过∠ABC的正切值可以用含a的式子表示出BC的长，从而可以解答本题．
【详解】解：由题意可得，
在Rt△ABC中，tan∠ABC=，
∴tan28.2°=，
∴，
故选：B．
【点睛】本题考查解直角三角形的应用，解答本题的关键是明确题意，利用锐角三角函数解答．
10．B
【分析】此题考查了垂径定理，等边三角形的性质，解直角三角形，
过点O作交于点D，连接，根据等边三角形的性质得到，然后由垂径定理得到，然后利用的余弦值求解即可．
【详解】过点O作交于点D，连接
∵是等边三角形
∴，
∵等边三角形内接于，
∴
∵
∴
∴．
故选：B．
11．C
【分析】本题考查网格中求三角函数值，涉及网格性质、勾股定理、相似的判定与性质，网格中求角的角的正切值等知识，利用网格中小正方形对角线垂直或平行，作出辅助线，如图所示，再结合相似三角形的判定与性质得到，最后在中，利用正切函数值定义，数形结合代值求解即可得到答案，利用网格性质构造辅助线是解决问题的关键．
【详解】解：设正方形网格中每个小正方形的边长为个单位长度，如图所示：
，，
，
，
，，
，
，
，
，
故选：C．
12．B
【分析】根据正弦的定义计算，得到答案．
【详解】解：为跷跷板的中点，，
，
在中，，
则，
故选：B．
【点睛】本题考查的是解直角三角形的应用坡度坡角问题，掌握正弦的定义是解题的关键．
13．10
【分析】根据直角三角形的三角函数得出AE，BE，进而得出CE，利用勾股定理得出AC即可．
【详解】解：如图，
∵BC⊥AE，
∴∠AEB=90°，
∵∠EAB=30°，AB=10千米，
∴BE=5米，AE=5千米，
∴CE=BC-BE=20-5=15（千米），
∴AC= （千米），
故答案为：10．
【点睛】本题考查解直角三角形的应用，关键是根据直角三角形的三角函数得出AE，BE解答．
14．(﹣2，2)
【分析】过点A作AC⊥OB于点C，根据△AOB是等边三角形，OB＝4可得出OC＝BC＝2，∠OAC＝∠OAB＝30°．在Rt△AOC中，根据∠OAC＝30°，OA＝4可得出AC及OC的长，进而得出A点坐标．
【详解】过点A作AC⊥OB于点C，
∵△AOB是等边三角形，OB＝4，
∴OC＝BC＝2，∠OAC＝∠OAB＝30°，
在Rt△AOC中，
∵∠OAC＝30°，OA＝4，
∴OC＝2，AC＝OA cos30°＝4×＝2
∵点A在第三象限，
∴A（﹣2，2）．
故答案为：（﹣2，2）．
【点睛】本题考查的是等边三角形的性质，熟知等边三角形三线合一的性质是解答此题的关键．
15．140
【分析】本题主要考查了解直角三角形的应用-方向角问题．正确作出辅助线构造直角三角形成为解题的关键．
如图：过作于，在中解直角三角形可得、，再在中可得，然后根据线段的和差即可解答．
【详解】解：如图：过作于，
在中，，海里，
（海里），（海里），
在中，，
海里，
（海里）．
16．4
【分析】在∠BAC的外部作∠CAE＝15°，作BF⊥AE于F，交AD于P，此时PA+2PB＝2＝＝2BF，通过解直角三角形ABF，进一步求得结果．
【详解】解：如图，
在∠BAC的外部作∠CAE＝15°，作BF⊥AE于F，交AD于P，
此时PA+2PB最小，
∴∠AFB＝90°
∵AB＝AC，AD⊥BC，
∴∠CAD＝∠BAD＝，
∴∠EAD＝∠CAE+∠CAD＝30°，
∴PF＝，
∴PA+2PB＝2＝＝2BF，
在Rt△ABF中，AB＝4，∠BAF＝∠BAC+∠CAE＝45°，
∴BF＝AB sin45°＝4，
∴（PA+2PB）最大＝2BF＝，
故答案为：．
【点睛】本题考查了等腰三角形的性质，解直角直角三角形，解题的关键是作辅助线．
17．3
【分析】本题考查了正切，反比例函数与一次函数的交点问题，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．
如图，过点A作轴，垂足为D，根据题意设出点A的坐标，然后根据一次函数的图象与反比例函数的图象相交于A、B两点，可以求得a的值，进而求得k的值即可．
【详解】解：如图，过点A作轴，垂足为D，
∵，
∴设点A的坐标为，
∵将直线沿y轴向下平移2个单位得到一次函数
与反比例函数的图象相交于A、B两点，
∴，
∴，
∴，
故答案为：3．
18．
【分析】根据零指数幂的运算法则，乘方的运算法则，特殊角的锐角三角形函数值，负指数幂的运算法则即可解答．
【详解】解：
．
【点睛】本题考查了零指数幂的运算法则，乘方的运算法则，特殊角的锐角三角形函数值，负指数幂的运算法则，有理数的加减混合运算法则，掌握对应法则是解题的关键．
19．（1）等腰三角形；（2）见解析，
【分析】（1）根据勾股定理求出OB和AB即可得出结论；
（2）根据作图步骤补全图形，利用锐角三角函数和全等三角形即可说明，然后利用待定系数法求直线AM的解析式即可．
【详解】解：（1）等腰三角形，理由如下
由坐标可知：OB=，AB=，OA=6
∴OB=AB
∴△ABO为等腰三角形
（2）第一步：在x正半轴上找一个格点E，使OE=OB=5；
第二步：找一个格点F（3,4），此时tan∠EOF==tan∠AOB，所以∠EOF=∠AOB；
第三步：找一个格点M（-4,1），作直线长AM交直线OF于D，连接DE，过点D作DG⊥x轴于点G
坐标系可知：tan∠DAG=，tan∠EOF=
∴，
设DG=4x，则OG=3x，AG=8x
根据勾股定理OD=，而AO=AG－OG=5x
∴OD=OA，
∵OE=OB，∠EOF=∠AOB，OD=OA
∴△OED≌OBA
则△DEO即为所作出的图形．
设直线AM的解析式为y=kx＋b
将点A、M的坐标代入，得
解得：
∴直线AM的解析式为
【点睛】此题考查的是勾股定理与网格问题、锐角三角函数、全等三角形的判定及性质和求一次函数解析式，掌握利用勾股定理、锐角三角函数解直角三角形、全等三角形的判定及性质和利用待定系数法求一次函数解析式是解决此题的关键．
20．(1)
(2)
【分析】本题考查解直角三角形，掌握直角三角形的边角关系是正确解答的关键．
（1）根据等腰三角形的性质，直角三角形的 边角关系进行计算即可；
（2）利用直角三角形的边角关系进行计算即可．
【详解】（1）解：∵，，，
∴，，
在中，，，
∴，
∴；
（2）解：如图，过点E作，垂足为G，
则，
∴，
答：拉绳的长为；
21．风筝的高度约为
【分析】本题考查了解直角三角形的应用仰角俯角问题，延长交于点，根据题意可：，， ，然后设，则，从而分别在和中，利用锐角三角函数的定义求出的长，最后列出关于的方程，进行计算即可解答．
【详解】解：延长交于点，
由题意得：.，， ，
设，
，
在中，，
，
在中，，
，
，
解得：
，
风筝的高度约为．
22．山体的长度为
【分析】本题考查了解直角三角形的应用仰角俯角问题，矩形的性质，根据等腰直角三角形的性质得到，求得，过作于，根据三角函数的定义即可得到结论，熟练掌握正确地作出辅助线是解题的关键．
【详解】解：无人机飞行速度为，
，，
，
，
过作于，
则，，
，，
，
，
答：山体的长度为．
23．(1)见解析
(2)
【分析】（1）计算出∠ADB和∠BAC，利用等角对等边即可证明；
（2）利用锐角三角函数求出BC即可计算△ABC的面积．
【详解】（1）证明：∵BD平分∠ABC，∠ABC＝60°，
∴∠DBC＝∠ABC＝30°．
∵∠C＝45°，
∴∠BDA＝∠DBC＋∠C＝75°，∠BAC＝180°－∠ABC－∠C＝75°．
∴∠BDA＝∠BAC．
∴AB＝BD．
（2）∵AE⊥BC，
∴∠AEB＝∠AEC＝90°．
在Rt△ABE中，∠ABC＝60°，AE＝3，
∴BE＝．
在Rt△AEC中，∠C＝45°，AE＝3，
∴EC＝．
∴BC＝BE＋EC＝．
∴S△ABC＝BC·AE＝．
【点睛】本题考查等腰三角形的判定以及利用锐角三角函数求值，解题的关键是求出∠ADB和∠BAC的度数．
24．(1)＝
(2)见解析
(3)
【分析】（1）由同圆中相等的圆周角所对的弧相等即可得结论；
（2）连接，由等腰三角形的性质及角平分线的定义可得，再结合即可完成证明；
（3）连接，过点O作于点F，由已知易得是等边三角形，从而可求得扇形的面积，再求出的长，即可求出的面积，从而求出阴影部分面积．
【详解】（1）解：∵平分，
∴，
∴；
故答案为：＝；
（2）证明：连接

∵，
∴．
∵平分，
∴．
∴．
∴．
∴．
∵，
∴．
∴．
∴．
∵为的半径，
∴是的切线．
（3）解：连接，过点O作于点F，

∵，
∴是等腰三角形．
∵平分，
∴．
∴是等边三角形．
∴．
∴．
在中，．
∴．
∴．
【点睛】本题是圆的综合，考查了圆周角与弧的关系，等边三角形的判定与性质，解直角三角形，切线的判定，求不规则图形的面积等知识，熟练掌握并正确运用这些知识是解题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)