12.4全等三角形同步练习(含解析)
文档属性
| 名称 | 12.4全等三角形同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-14 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
12.4全等三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知,,则的长为( )
A.4 B.5 C.6 D.7
2.如图,已知,下列结论:①;②;③;④;⑤;⑥;⑦.其中正确的有( )
A.个 B.个 C.个 D.个
3.已知图中的两个三角形全等,则等于( )
A. B. C. D.
4.如图,,,,则AC为( )
A.3 B.4 C.5 D.6
5.如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,且A、C、B在同一直线上,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN;④PC平分∠APB;⑤∠APD=60°,其中正确结论有( )
A.5个 B.4个 C.3个 D.2个
6.如下图,已知,点恰好在的延长线上,,.则的度数是( )
A. B. C. D.
7.如图,若两个三角形全等,则的度数是( )
A. B. C. D.
8.如图,和是两个直角三角形,且点B,C,D在同一条直线上,若,则线段和线段的关系是( )
A.既不相等又不互相垂直 B.相等但不互相垂直
C.互相垂直但不相等 D.相等且互相垂直
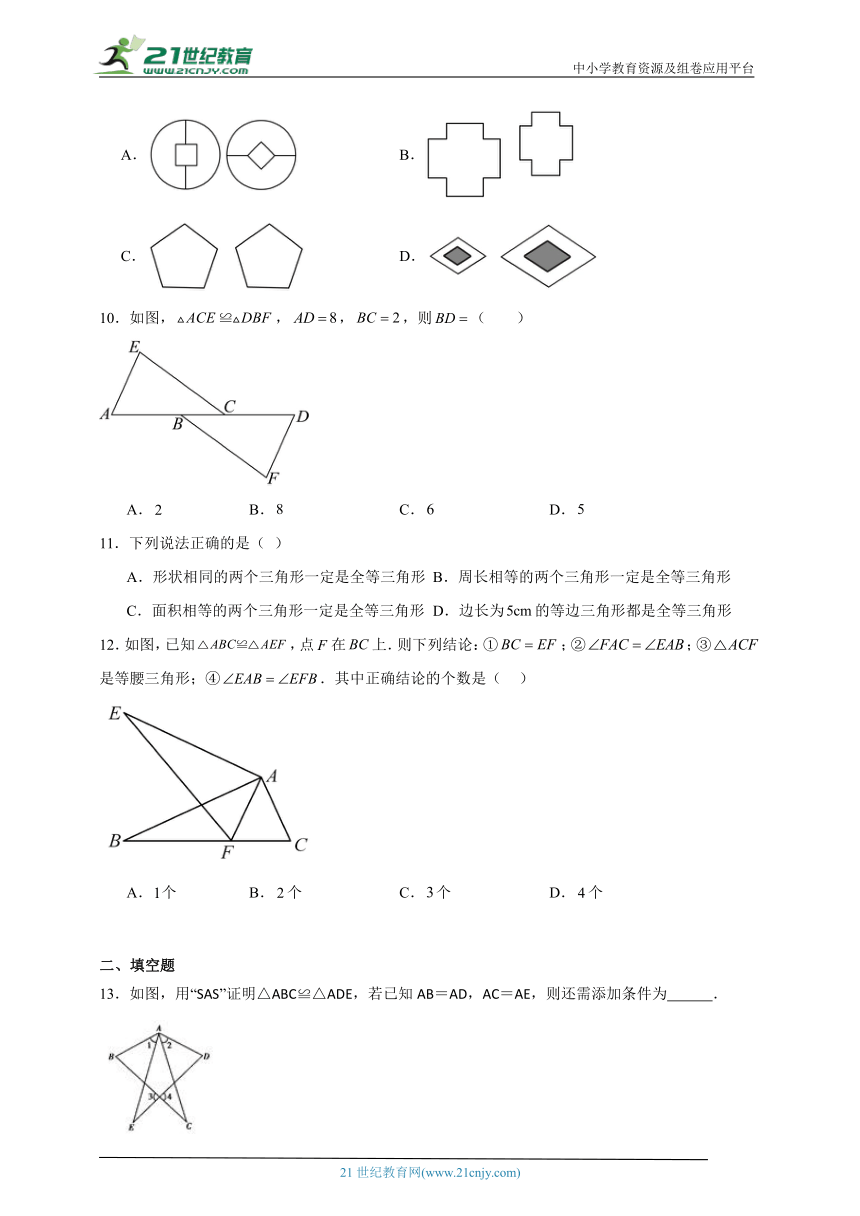
9.下列各项中,两个图形属于全等图形的是( )
A. B.
C. D.
10.如图,,,,则( )
A. B. C. D.
11.下列说法正确的是( )
A.形状相同的两个三角形一定是全等三角形 B.周长相等的两个三角形一定是全等三角形
C.面积相等的两个三角形一定是全等三角形 D.边长为的等边三角形都是全等三角形
12.如图,已知,点在上.则下列结论:①;②;③是等腰三角形;④.其中正确结论的个数是( )
A.个 B.个 C.个 D.个
二、填空题
13.如图,用“SAS”证明△ABC≌△ADE,若已知AB=AD,AC=AE,则还需添加条件为 .
14.如图,,垂足为点A,厘米,厘米,射线,垂足为点B,一动点E从A点出发以0.5厘米/秒的速度沿射线运动,点D为射线上一动点,随着E点运动而运动,且始终保持,当点E离开点A后,运动 秒时,与全等.(将选择与填空题的答案填在答题纸对应的位置上)
15.全等三角形不能重合. ( )
16.能够完全重合的两个图形叫做 .如果两个图形全等.它们的形状和大小一定 .
17.如图,,且点B,C,E共线,若的面积为6,,则 .
三、解答题
18.综合与探究
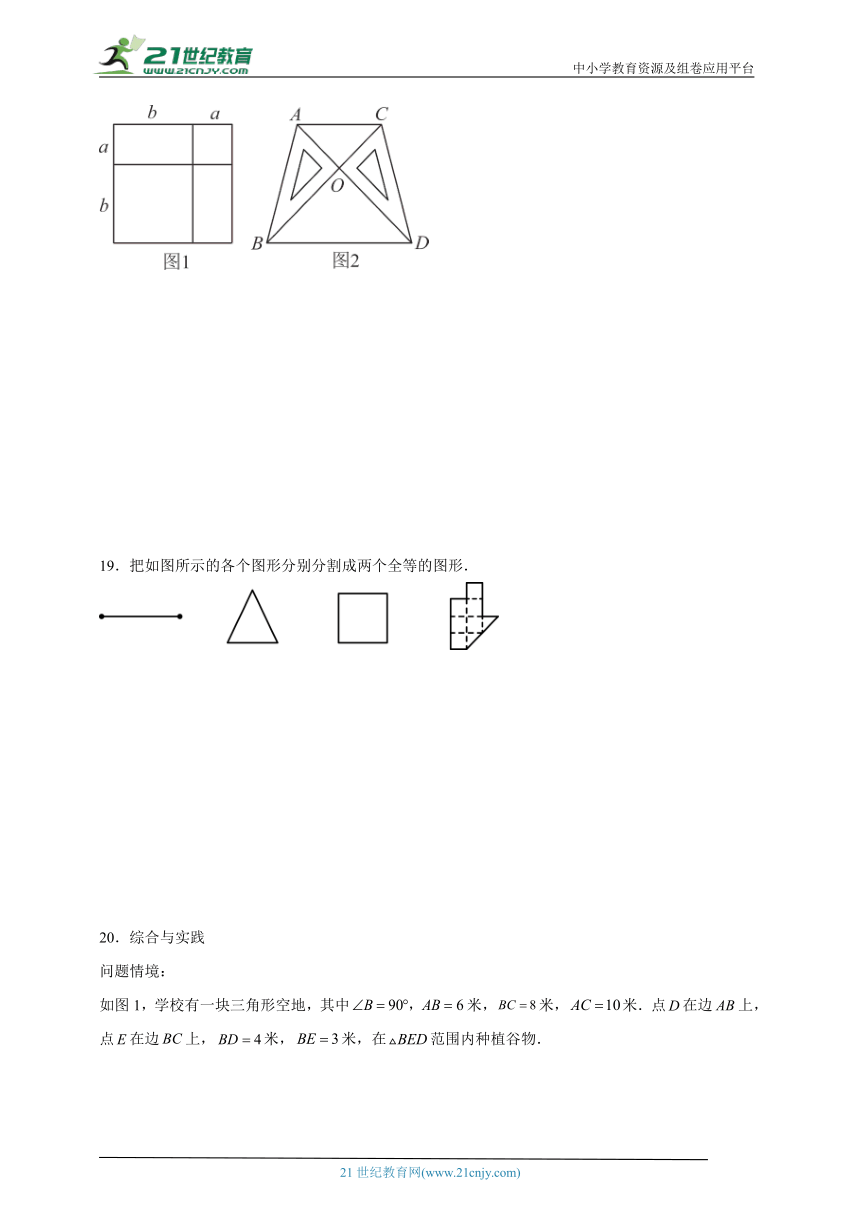
【知识生成】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如,由图1可以得到,基于此,请解答下列问题.
【直接应用】(1)若,,求的值.
【类比应用】(2)若,则___________.
【知识迁移】(3)将两块全等的特制直角三角板()按如图2所示的方式放置,其中点,,在同一直线上,点,,也在同一直线上,连接,.若,,求一块直角三角板的面积.
19.把如图所示的各个图形分别分割成两个全等的图形.
20.综合与实践
问题情境:
如图1,学校有一块三角形空地,其中米,米,米.点在边上,点在边上,米,米,在范围内种植谷物.
思考探究:
(1)种植谷物的面积为_________平方米.
方案设计:
现需要在剩余空地上分割出一块三角形空地种植玉米(为种植玉米三角形空地的一个顶点),其面积与种植谷物的面积相同.
(2)可以利用全等三角形面积相等的方法设计方案.
①欣欣的方案:如图2,在边上选取一点,在边上选取点,当时,即可使种植玉米的面积与种植谷物的面积相同,求此时的长.
②彤彤认为还有其他全等情况也符合设计要求,请直接写出其他符合设计要求的方案中的长.(点在边上,点在边上)
(3)畅畅想到了利用中线分割的方法,如图3,选取的中点,连接,选取的中点,连接,则即为符合条件的种植玉米的三角形空地.请说明畅畅的想法是否正确,并说明理由.
21.在校运动会上,某校七年级⑴班的同学为了给参加比赛的同学加油助威,每人提前制作了一面同一规格的直角三角形彩旗.小明放学回家后,发现自己的彩旗破损了一角(如图1),他想用如图2所示的长方形彩纸重新制作一面彩旗.请你帮助小明,用直尺与圆规在彩纸上作出一个与破损前完全一样的三角形.(不写作法,保留作图痕迹)
22.如图,已知BE,CF分别是△ABC中AC,AB边上的高线,在BE的延长线上取点P,使PB=AC,在CF的延长线上取点Q,使CQ=AB.求证:AQ⊥AP.
23.如图所示,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
(1)判断FC与AD的数量关系,并说明理由;
(2)若∠D=90°,AE平分∠BAD,求证:BE平分∠ABC.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D C B C A D C D
题号 11 12
答案 D D
1.B
【分析】本题主要考查全等三角形的性质,熟练掌握全等三角形对应边相等是解题的关键.由全等三角形的性质得到即可得到答案.
【详解】解:,
,
,
.
故选B.
2.C
【分析】利用得到对应边和对应角相等可以推出①③,根据对应角相等、对应边相等可推出②④⑦,再根据全等三角形面积相等可推出⑤,正确;根据已知条件不能推出⑥.
【详解】解:①∵
∴故①正确;
②∵
∴即:,故②正确;
③∵
∴;
∴即:,故③正确;
④∵
∴;
∴,故④正确;
⑤∵
∴,故⑤正确;
⑥根据已知条件不能证得,故⑥错误;
⑦∵
∴;
∴,故⑦正确;
故①②③④⑤⑦,正确的6个.
故选C.
【点睛】本题考查了全等三角形的性质,正确掌握全等三角形对应边相等,对应角相等是解答此题的关键.
3.D
【分析】本题考查全等三角形的性质,根据三角形内角和定理求得,然后由全等三角形的性质可得结论.解题的关键是掌握:全等三角形的对应角相等.
【详解】解:如图,
,
∵图中的两个三角形全等,
∴.
故选:D.
4.C
【分析】根据全等三角形的性质得出,进而根据线段的和差即可求解.
【详解】解:∵,
∴
∵,,
∴,
∴
故选:C.
【点睛】本题考查了全等三角形的性质,熟练掌握全等三角形的性质是解题的关键.
5.B
【分析】利用边角边即可证明△ACE与△DCB全等,然后根据全等三角形对应角相等可得∠CAM=∠CDN,再利用角边角证明△ACM≌△DCN,根据全等三角形对应边相等可得CM=CN,DN=AM,同理可证明△BCN≌△ECM,根据全等三角形对应边相等可得BN=EM,根据三角形面积公式求出CQ=CH,即可判断④,根据三角形外角性质推出∠APD=60°.
【详解】∵△DAC和△EBC都是等边三角形,
∴∠ACD=∠BCE=60°,
∴∠ACE=∠DCB=120°,
在△ACE与△DCB中,
AC=DC,∠ACE=∠DCB,CB=CE,
∴△ACE≌△DCB(SAS),故①正确;
∴∠CAM=∠CDN,
在△ACM与△DCN中
∠CAM=∠CDN,AC=DC,∠ACM=∠DCN=60°,
∴△ACM≌△DCN(ASA),
∴CM=CN,故②正确;
DN=AM,
在△AMC中,AC>AM,
∴AC≠DN,故③错误;
过C作CQ⊥DB于Q,CH⊥AE于H,
∵△ACM≌△DCN,
∴△ACM和△DCN的面积相等,
∵DN=AM,
∴由三角形面积公式得:CQ=CH,
∴CP平分∠APB,∴④正确;
∵△ACE≌△DCB,
∴∠AEC=∠DBC,
∵∠ECB=60°,
∴∠EAC+∠AEC=∠ECB=60°,
∴∠APD=∠EAC+∠ABP=∠EAC+∠AEC=60°
∴⑤正确;
故选B.
【点睛】本题考查的是全等三角形的性质,熟练掌握全等三角形是解题的关键.
6.C
【分析】本题考查了三角形内角和,以及全等三角形性质,根据三角形内角和得到,再利用全等三角形性质推出,最后各角平角的定义,即可解题.
【详解】解:,,
,
,
,
点恰好在的延长线上,
,
故选:C.
7.A
【分析】三角形内角和定理求出的度数,全等三角形的性质,得到,即可得解.
【详解】解:如图,
由三角形的内角和定理,得:,
∵两个三角形全等,由图可知,为对应角,
∴,
故选A.
【点睛】本题考查全等三角形的性质,解题的关键是掌握全等三角形的对应角相等.
8.D
【分析】本题考查三角形全等的性质,根据得到,,,结合直角三角形的性质即可得到答案
【详解】解:∵,
∴,,,,
∴,
∴,
∴线段和线段相等且互相垂直,
故选:D.
9.C
【分析】利用全等图形的概念:能够完全重合的两个图形叫做全等形可得答案.
【详解】解:A、两个图形不能完全重合,不是全等图形,不符合题意;
B、两个图形不能完全重合,不是全等图形,不符合题意;
C、两个图形能够完全重合,是全等图形,符合题意;
D、两个图形不能完全重合,不是全等图形,不符合题意;
故选:C.
【点睛】本题考查的是全等形的识别、全等图形的基本性质,属于较容易的基础题.
10.D
【分析】本题考查了全等三角形的性质,根据全等三角形对应边相等可得,再求出,在根据线段和差即可求解,熟练掌握全等三角形的性质是解题的关键.
【详解】∵,
∴,
∴,即,
∵,,
∴,
∴,
故选:D.
11.D
【分析】根据全等三角形的定义:能够完全重合的两个三角形为全等三角形,据此判断即可.
【详解】A、形状相同且大小相同的两个三角形一定是全等三角形,原说法错误,不符合题意;
B、周长相等的两个三角形不一定是全等三角形,原说法错误,不符合题意;
C、面积相等的两个三角形不一定是全等三角形,原说法错误,不符合题意;
D、边长为的等边三角形都是全等三角形,原说法正确,符合题意;
故选:D.
【点睛】本题考查了全等三角形的定义,熟记定义是解本题的关键.
12.D
【分析】根据全等三角形的性质,即可.
【详解】∵,
∴,,,
∴①正确;
∵,
∴,
∴,
∴②正确;
∵,
∴是等腰三角形,
∴③正确;
∵绕点旋转得到,
∴,
∴,
∴④正确;
∴正确的有:①②③④.
故选:D.
【点睛】本题考查旋转,全等三角形的知识,解题的关键是掌握全等三角形的性质,旋转的性质.
13.∠BAC=∠DAE.
【分析】根据题目中给出的条件AB=AD,AC=AE,要用“SAS”还缺少条件是夹角:∠BAC=∠DAE.
【详解】还需条件∠BAC=∠DAE.理由如下:
在△ABC和△ADE中,∵,∴△ABC≌△ADE(SAS).
故答案为∠BAC=∠DAE.
【点睛】本题主要考查了全等三角形的判定,关键是要熟记判定定理:SSS,SAS,AAS,ASA.
14.12或32或44
【分析】分两种情况:①当E在线段上时,②当E在上,再分别分成两种情况,进行计算即可.
【详解】解:①当E在线段上,时,,
∵,
∴,
∴,
∴点E的运动时间为秒;
②当E在上,时,
∵,
∴,
∴,
∴点E的运动时间为秒;
③当E在线段上,时,,
这时E在A点未动,因此时间为0秒;
④当E在上,时,,
,
点E的运动时间为秒.
故答案为:12或32或44.
【点睛】本题主要考查了全等三角形的性质,利用分类讨论的思想分析三角形全等是解决问题的关键.
15.错
【分析】根据全等三角形的性质判断即可.
【详解】解:根据全等三角形的性质可知,两个三角形全等,则对应角、对应边相等,故两个三角形重合.
故答案为错.
【点睛】本题主要考查全等三角形的性质,掌握全等三角形的对应角、对应边相等是解题的关键.
16. 全等形 相等
【解析】略
17.1
【分析】设,且,根据得,,则,由的面积为6得进一步得到,即可得到答案.
【详解】解:设,且,
∵,
∴,,
∴,
∵的面积为6,
∴,
∴,
∵,
∴.
故答案为:1
【点睛】此题考查了全等三角形的性质、完全平方公式、算术平方根等知识,数形结合是解题的关键.
18.(1);(2);(3)
【分析】(1)根据完全平方公式变形即可求解.
(2)将看成,进而根据,即可求解;
(3)设,,根据可得,而,进而根据完全平方公式变形即可求解.
【详解】解:(1)
又
,
;
(2)∵,则
故答案为:;
(3)∵两块直角三角板全等,
,,
点A,O,D在同一直线上,点B,O,C也在同一直线上,
,.
设,.
,
又,
,
,
,
,
答:一块直角三角板的面积为16.
【点睛】本题考查了完全平方公式变形求值,全等三角形的性质,熟练掌握完全平方公式是解题的关键.
19.见解析
【分析】此题考查全等图形,关键是根据全等图形的性质解答.
根据全等图形的性质解答即可.
【详解】解:如图所示:
20.(1)6;(2)①米;②当时,米;(3)正确,理由见解析
【分析】本题考查了全等三角形的性质,三角形中线的性质,灵活运用各知识点是解答本题的关键.
(1)利用三角形的面积公式计算即可;
(2)①当时,米,进而可求出的长;
②当时,米,进而可求出的长;
(3)根据中线的性质求出的面积,即可判断畅畅的想法是否正确.
【详解】解:(1)∵,米,米,
∴种植谷物的面积平方米.
故答案为:6;
(2)①∵,
∴米,
∴米;
②当时,
则米,
∴米;
(3)∵米,米,
∴平方米.
∵P是的中点,
∴平方米.
∵Q是的中点,
∴平方米.
∴,
∴畅畅的想法正确.
21.作图见详解
【分析】由题意根据作三角形全等于已知三角形的方法利用ASA,在矩形的较短的边上截取线段等于彩旗的短直角边,再作一角等于彩旗的顶角即可.
【详解】解:如图所示:
【点睛】本题主要考查全等三角形的判定与性质以及应用与设计作图,熟练并正确利用全等三角形的判定进行分析是解题的关键.
22.见解析
【分析】由垂直定义得∠AEB=∠AFC=90°,通过△ABP≌△QCA,根据全等三角形的性质得到∠APB=∠QAC,由于∠APB+∠PAE=∠QAC+∠PAE,故得到∠PAQ=90°,可得出结论.
【详解】∵BE,CF分别是△ABC中AC,AB边上的高线,
∴∠AEB=∠AFC=90°,
∴∠ABP+∠EAF=90°,∠ACQ+∠EAF=90°,
∴∠ABP=∠ACQ.
在△ABP和△QCA中,
∵
∴△ABP≌△QCA(SAS).
∴∠APB=∠QAC.
∴∠APB+∠PAE=∠QAC+∠PAE,
即180°-∠AEP=∠PAQ.
∴∠PAQ=90°,
即AQ⊥AP.
【点睛】本题考查的是全等三角形的性质与判定,熟知全等三角形的SAS、ASA及SSS定理是解答此题的关键.
23.(1)FC=AD,见解析
(2)见解析
【详解】(1)(1)解:结论:CF=AD.
理由:∵AD∥BC,
∴∠ADC=∠ECF,
∵E是CD的中点,
∴DE=EC,
∵在△ADE与△FCE中
∴△ADE≌△FCE(ASA)
∴FC=AD;
(2)(2)证明:过点E作EH⊥AB,垂足为H.
∵AD∥BC,∠D=90°,
∴∠DCB=90°.
∵AE平分∠BAD,∠D=90°,EH⊥AB于H,
∴DE=EH.
∵E是CD的中点,
∴DE=EC,
∴EH=EC,
∵∠DCB=90°,EH⊥AB于H,
∴BE平分∠ABC.
【点睛】本题考查全等三角形的判定和性质、等腰三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
12.4全等三角形
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,已知,,则的长为( )
A.4 B.5 C.6 D.7
2.如图,已知,下列结论:①;②;③;④;⑤;⑥;⑦.其中正确的有( )
A.个 B.个 C.个 D.个
3.已知图中的两个三角形全等,则等于( )
A. B. C. D.
4.如图,,,,则AC为( )
A.3 B.4 C.5 D.6
5.如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,且A、C、B在同一直线上,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN;④PC平分∠APB;⑤∠APD=60°,其中正确结论有( )
A.5个 B.4个 C.3个 D.2个
6.如下图,已知,点恰好在的延长线上,,.则的度数是( )
A. B. C. D.
7.如图,若两个三角形全等,则的度数是( )
A. B. C. D.
8.如图,和是两个直角三角形,且点B,C,D在同一条直线上,若,则线段和线段的关系是( )
A.既不相等又不互相垂直 B.相等但不互相垂直
C.互相垂直但不相等 D.相等且互相垂直
9.下列各项中,两个图形属于全等图形的是( )
A. B.
C. D.
10.如图,,,,则( )
A. B. C. D.
11.下列说法正确的是( )
A.形状相同的两个三角形一定是全等三角形 B.周长相等的两个三角形一定是全等三角形
C.面积相等的两个三角形一定是全等三角形 D.边长为的等边三角形都是全等三角形
12.如图,已知,点在上.则下列结论:①;②;③是等腰三角形;④.其中正确结论的个数是( )
A.个 B.个 C.个 D.个
二、填空题
13.如图,用“SAS”证明△ABC≌△ADE,若已知AB=AD,AC=AE,则还需添加条件为 .
14.如图,,垂足为点A,厘米,厘米,射线,垂足为点B,一动点E从A点出发以0.5厘米/秒的速度沿射线运动,点D为射线上一动点,随着E点运动而运动,且始终保持,当点E离开点A后,运动 秒时,与全等.(将选择与填空题的答案填在答题纸对应的位置上)
15.全等三角形不能重合. ( )
16.能够完全重合的两个图形叫做 .如果两个图形全等.它们的形状和大小一定 .
17.如图,,且点B,C,E共线,若的面积为6,,则 .
三、解答题
18.综合与探究
【知识生成】我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如,由图1可以得到,基于此,请解答下列问题.
【直接应用】(1)若,,求的值.
【类比应用】(2)若,则___________.
【知识迁移】(3)将两块全等的特制直角三角板()按如图2所示的方式放置,其中点,,在同一直线上,点,,也在同一直线上,连接,.若,,求一块直角三角板的面积.
19.把如图所示的各个图形分别分割成两个全等的图形.
20.综合与实践
问题情境:
如图1,学校有一块三角形空地,其中米,米,米.点在边上,点在边上,米,米,在范围内种植谷物.
思考探究:
(1)种植谷物的面积为_________平方米.
方案设计:
现需要在剩余空地上分割出一块三角形空地种植玉米(为种植玉米三角形空地的一个顶点),其面积与种植谷物的面积相同.
(2)可以利用全等三角形面积相等的方法设计方案.
①欣欣的方案:如图2,在边上选取一点,在边上选取点,当时,即可使种植玉米的面积与种植谷物的面积相同,求此时的长.
②彤彤认为还有其他全等情况也符合设计要求,请直接写出其他符合设计要求的方案中的长.(点在边上,点在边上)
(3)畅畅想到了利用中线分割的方法,如图3,选取的中点,连接,选取的中点,连接,则即为符合条件的种植玉米的三角形空地.请说明畅畅的想法是否正确,并说明理由.
21.在校运动会上,某校七年级⑴班的同学为了给参加比赛的同学加油助威,每人提前制作了一面同一规格的直角三角形彩旗.小明放学回家后,发现自己的彩旗破损了一角(如图1),他想用如图2所示的长方形彩纸重新制作一面彩旗.请你帮助小明,用直尺与圆规在彩纸上作出一个与破损前完全一样的三角形.(不写作法,保留作图痕迹)
22.如图,已知BE,CF分别是△ABC中AC,AB边上的高线,在BE的延长线上取点P,使PB=AC,在CF的延长线上取点Q,使CQ=AB.求证:AQ⊥AP.
23.如图所示,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,延长AE交BC的延长线于点F.
(1)判断FC与AD的数量关系,并说明理由;
(2)若∠D=90°,AE平分∠BAD,求证:BE平分∠ABC.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B C D C B C A D C D
题号 11 12
答案 D D
1.B
【分析】本题主要考查全等三角形的性质,熟练掌握全等三角形对应边相等是解题的关键.由全等三角形的性质得到即可得到答案.
【详解】解:,
,
,
.
故选B.
2.C
【分析】利用得到对应边和对应角相等可以推出①③,根据对应角相等、对应边相等可推出②④⑦,再根据全等三角形面积相等可推出⑤,正确;根据已知条件不能推出⑥.
【详解】解:①∵
∴故①正确;
②∵
∴即:,故②正确;
③∵
∴;
∴即:,故③正确;
④∵
∴;
∴,故④正确;
⑤∵
∴,故⑤正确;
⑥根据已知条件不能证得,故⑥错误;
⑦∵
∴;
∴,故⑦正确;
故①②③④⑤⑦,正确的6个.
故选C.
【点睛】本题考查了全等三角形的性质,正确掌握全等三角形对应边相等,对应角相等是解答此题的关键.
3.D
【分析】本题考查全等三角形的性质,根据三角形内角和定理求得,然后由全等三角形的性质可得结论.解题的关键是掌握:全等三角形的对应角相等.
【详解】解:如图,
,
∵图中的两个三角形全等,
∴.
故选:D.
4.C
【分析】根据全等三角形的性质得出,进而根据线段的和差即可求解.
【详解】解:∵,
∴
∵,,
∴,
∴
故选:C.
【点睛】本题考查了全等三角形的性质,熟练掌握全等三角形的性质是解题的关键.
5.B
【分析】利用边角边即可证明△ACE与△DCB全等,然后根据全等三角形对应角相等可得∠CAM=∠CDN,再利用角边角证明△ACM≌△DCN,根据全等三角形对应边相等可得CM=CN,DN=AM,同理可证明△BCN≌△ECM,根据全等三角形对应边相等可得BN=EM,根据三角形面积公式求出CQ=CH,即可判断④,根据三角形外角性质推出∠APD=60°.
【详解】∵△DAC和△EBC都是等边三角形,
∴∠ACD=∠BCE=60°,
∴∠ACE=∠DCB=120°,
在△ACE与△DCB中,
AC=DC,∠ACE=∠DCB,CB=CE,
∴△ACE≌△DCB(SAS),故①正确;
∴∠CAM=∠CDN,
在△ACM与△DCN中
∠CAM=∠CDN,AC=DC,∠ACM=∠DCN=60°,
∴△ACM≌△DCN(ASA),
∴CM=CN,故②正确;
DN=AM,
在△AMC中,AC>AM,
∴AC≠DN,故③错误;
过C作CQ⊥DB于Q,CH⊥AE于H,
∵△ACM≌△DCN,
∴△ACM和△DCN的面积相等,
∵DN=AM,
∴由三角形面积公式得:CQ=CH,
∴CP平分∠APB,∴④正确;
∵△ACE≌△DCB,
∴∠AEC=∠DBC,
∵∠ECB=60°,
∴∠EAC+∠AEC=∠ECB=60°,
∴∠APD=∠EAC+∠ABP=∠EAC+∠AEC=60°
∴⑤正确;
故选B.
【点睛】本题考查的是全等三角形的性质,熟练掌握全等三角形是解题的关键.
6.C
【分析】本题考查了三角形内角和,以及全等三角形性质,根据三角形内角和得到,再利用全等三角形性质推出,最后各角平角的定义,即可解题.
【详解】解:,,
,
,
,
点恰好在的延长线上,
,
故选:C.
7.A
【分析】三角形内角和定理求出的度数,全等三角形的性质,得到,即可得解.
【详解】解:如图,
由三角形的内角和定理,得:,
∵两个三角形全等,由图可知,为对应角,
∴,
故选A.
【点睛】本题考查全等三角形的性质,解题的关键是掌握全等三角形的对应角相等.
8.D
【分析】本题考查三角形全等的性质,根据得到,,,结合直角三角形的性质即可得到答案
【详解】解:∵,
∴,,,,
∴,
∴,
∴线段和线段相等且互相垂直,
故选:D.
9.C
【分析】利用全等图形的概念:能够完全重合的两个图形叫做全等形可得答案.
【详解】解:A、两个图形不能完全重合,不是全等图形,不符合题意;
B、两个图形不能完全重合,不是全等图形,不符合题意;
C、两个图形能够完全重合,是全等图形,符合题意;
D、两个图形不能完全重合,不是全等图形,不符合题意;
故选:C.
【点睛】本题考查的是全等形的识别、全等图形的基本性质,属于较容易的基础题.
10.D
【分析】本题考查了全等三角形的性质,根据全等三角形对应边相等可得,再求出,在根据线段和差即可求解,熟练掌握全等三角形的性质是解题的关键.
【详解】∵,
∴,
∴,即,
∵,,
∴,
∴,
故选:D.
11.D
【分析】根据全等三角形的定义:能够完全重合的两个三角形为全等三角形,据此判断即可.
【详解】A、形状相同且大小相同的两个三角形一定是全等三角形,原说法错误,不符合题意;
B、周长相等的两个三角形不一定是全等三角形,原说法错误,不符合题意;
C、面积相等的两个三角形不一定是全等三角形,原说法错误,不符合题意;
D、边长为的等边三角形都是全等三角形,原说法正确,符合题意;
故选:D.
【点睛】本题考查了全等三角形的定义,熟记定义是解本题的关键.
12.D
【分析】根据全等三角形的性质,即可.
【详解】∵,
∴,,,
∴①正确;
∵,
∴,
∴,
∴②正确;
∵,
∴是等腰三角形,
∴③正确;
∵绕点旋转得到,
∴,
∴,
∴④正确;
∴正确的有:①②③④.
故选:D.
【点睛】本题考查旋转,全等三角形的知识,解题的关键是掌握全等三角形的性质,旋转的性质.
13.∠BAC=∠DAE.
【分析】根据题目中给出的条件AB=AD,AC=AE,要用“SAS”还缺少条件是夹角:∠BAC=∠DAE.
【详解】还需条件∠BAC=∠DAE.理由如下:
在△ABC和△ADE中,∵,∴△ABC≌△ADE(SAS).
故答案为∠BAC=∠DAE.
【点睛】本题主要考查了全等三角形的判定,关键是要熟记判定定理:SSS,SAS,AAS,ASA.
14.12或32或44
【分析】分两种情况:①当E在线段上时,②当E在上,再分别分成两种情况,进行计算即可.
【详解】解:①当E在线段上,时,,
∵,
∴,
∴,
∴点E的运动时间为秒;
②当E在上,时,
∵,
∴,
∴,
∴点E的运动时间为秒;
③当E在线段上,时,,
这时E在A点未动,因此时间为0秒;
④当E在上,时,,
,
点E的运动时间为秒.
故答案为:12或32或44.
【点睛】本题主要考查了全等三角形的性质,利用分类讨论的思想分析三角形全等是解决问题的关键.
15.错
【分析】根据全等三角形的性质判断即可.
【详解】解:根据全等三角形的性质可知,两个三角形全等,则对应角、对应边相等,故两个三角形重合.
故答案为错.
【点睛】本题主要考查全等三角形的性质,掌握全等三角形的对应角、对应边相等是解题的关键.
16. 全等形 相等
【解析】略
17.1
【分析】设,且,根据得,,则,由的面积为6得进一步得到,即可得到答案.
【详解】解:设,且,
∵,
∴,,
∴,
∵的面积为6,
∴,
∴,
∵,
∴.
故答案为:1
【点睛】此题考查了全等三角形的性质、完全平方公式、算术平方根等知识,数形结合是解题的关键.
18.(1);(2);(3)
【分析】(1)根据完全平方公式变形即可求解.
(2)将看成,进而根据,即可求解;
(3)设,,根据可得,而,进而根据完全平方公式变形即可求解.
【详解】解:(1)
又
,
;
(2)∵,则
故答案为:;
(3)∵两块直角三角板全等,
,,
点A,O,D在同一直线上,点B,O,C也在同一直线上,
,.
设,.
,
又,
,
,
,
,
答:一块直角三角板的面积为16.
【点睛】本题考查了完全平方公式变形求值,全等三角形的性质,熟练掌握完全平方公式是解题的关键.
19.见解析
【分析】此题考查全等图形,关键是根据全等图形的性质解答.
根据全等图形的性质解答即可.
【详解】解:如图所示:
20.(1)6;(2)①米;②当时,米;(3)正确,理由见解析
【分析】本题考查了全等三角形的性质,三角形中线的性质,灵活运用各知识点是解答本题的关键.
(1)利用三角形的面积公式计算即可;
(2)①当时,米,进而可求出的长;
②当时,米,进而可求出的长;
(3)根据中线的性质求出的面积,即可判断畅畅的想法是否正确.
【详解】解:(1)∵,米,米,
∴种植谷物的面积平方米.
故答案为:6;
(2)①∵,
∴米,
∴米;
②当时,
则米,
∴米;
(3)∵米,米,
∴平方米.
∵P是的中点,
∴平方米.
∵Q是的中点,
∴平方米.
∴,
∴畅畅的想法正确.
21.作图见详解
【分析】由题意根据作三角形全等于已知三角形的方法利用ASA,在矩形的较短的边上截取线段等于彩旗的短直角边,再作一角等于彩旗的顶角即可.
【详解】解:如图所示:
【点睛】本题主要考查全等三角形的判定与性质以及应用与设计作图,熟练并正确利用全等三角形的判定进行分析是解题的关键.
22.见解析
【分析】由垂直定义得∠AEB=∠AFC=90°,通过△ABP≌△QCA,根据全等三角形的性质得到∠APB=∠QAC,由于∠APB+∠PAE=∠QAC+∠PAE,故得到∠PAQ=90°,可得出结论.
【详解】∵BE,CF分别是△ABC中AC,AB边上的高线,
∴∠AEB=∠AFC=90°,
∴∠ABP+∠EAF=90°,∠ACQ+∠EAF=90°,
∴∠ABP=∠ACQ.
在△ABP和△QCA中,
∵
∴△ABP≌△QCA(SAS).
∴∠APB=∠QAC.
∴∠APB+∠PAE=∠QAC+∠PAE,
即180°-∠AEP=∠PAQ.
∴∠PAQ=90°,
即AQ⊥AP.
【点睛】本题考查的是全等三角形的性质与判定,熟知全等三角形的SAS、ASA及SSS定理是解答此题的关键.
23.(1)FC=AD,见解析
(2)见解析
【详解】(1)(1)解:结论:CF=AD.
理由:∵AD∥BC,
∴∠ADC=∠ECF,
∵E是CD的中点,
∴DE=EC,
∵在△ADE与△FCE中
∴△ADE≌△FCE(ASA)
∴FC=AD;
(2)(2)证明:过点E作EH⊥AB,垂足为H.
∵AD∥BC,∠D=90°,
∴∠DCB=90°.
∵AE平分∠BAD,∠D=90°,EH⊥AB于H,
∴DE=EH.
∵E是CD的中点,
∴DE=EC,
∴EH=EC,
∵∠DCB=90°,EH⊥AB于H,
∴BE平分∠ABC.
【点睛】本题考查全等三角形的判定和性质、等腰三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
