第十三章事件与可能性同步练习(含解析)
文档属性
| 名称 | 第十三章事件与可能性同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 446.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-14 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第十三章事件与可能性
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列事件中,属于确定事件的有( )个.
①投掷一枚硬币,正面朝上;
②方程两根之积等于;
③经过红绿灯的十字路口,红绿灯为红灯;
④地球自转;
⑤在篮球比赛中,弱队战胜强队.
A.1 B.2 C.3 D.4
2.甲、乙两人做掷骰子游戏,规定:一人掷一次,若两人所掷骰子的点数和大于6,则甲胜;反之,乙胜.则甲、乙两人中( )
A.甲获胜的可能最大 B.乙获胜的可能最大
C.甲、乙获胜的可能一样大 D.由于是随机事件,因此无法估计
3.下列事件,是随机事件的是( )
A.一个三角形的内角和为 B.掷一枚股子,向上一面点数大于0
C.经过有交通信号灯的路口,遇到红灯 D.3人分成两组一定有2人分在一组
4.有六张背面完全相同的卡片,正面分别标有数字,从中分别抽取两张(放回), 则下列事件为随机事件的是( )
A.两张卡片的数字之和等于 B.两张卡片的数字之和大于
C.两张卡片的数字之和等于 D.两张卡片的数字之和大于
5.下列成语中,表示不可能事件的是( )
A.水中捞月 B.守株待兔 C.水涨船高 D.水滴石穿
6.下列事件为必然事件的是( )
A.打开电视机,它正在播广告 B.明天太阳从东方升起
C.某彩票的中奖机会是,买1张一定不会中奖 D.抛掷一枚硬币,一定正面朝上
7.下列事件为必然事件的是( ).
A.抛掷一枚普通的正方体骰子,掷得的点数不小于1
B.经过有交通信号灯的路口,遇到红灯
C.抛一枚普通的硬币,正面朝上
D.一年有367天
8.下列两个说法:
“抛一枚硬币正面朝上的概率是”表示抛硬币次必有次出现正面朝上;
“彩票中奖的概率是”表示买张彩票一定会中奖.
其中( )
A.都正确 B.只有正确 C.只有正确 D.两个说法都错误
9.下列事件为必然事件的是( )
A.购买两张彩票,一定中奖
B.打开电视,正在播放新闻联播
C.抛掷一枚硬币,正面向上
D.三角形三个内角和为
10.“用长分别为5cm、12cm、13cm的三条线段可以围成直角三角形”这一事件是( )
A.必然事件 B.不可能事件 C.随机事件 D.以上都不是
11.下列事件属于必然事件的是( )
A.实数a<0,则2a<0
B.我们班的同学将会有人成为航天员
C.打开电视,正在播放新闻
D.新疆的冬天不下雪
12.下列事件中,是随机事件的是( )
A.通常温度降到以下,纯净的水结冰
B.随意翻到一本书的某页,这页的页码是奇数
C.明天太阳从东方升起
D.任意画一个三角形,其内角和是
二、填空题
13.下列事件,①通常加热到 100℃,水沸腾;②在平面上,任意画一个三角形,其内角和小于 180°.其中是不可能事件的是 (只填写序号即可)
14.不透明的袋子中有除颜色外完全相同的4个红球和2个绿球,从袋子中随机摸出3个球,至少有1个红球是 .(填“随机事件”,“必然事件”或“不可能事件”)
15.一个不透明的袋子里装有3个红球,2个黄球,1个白球,这些球除颜色外无其他差别,从袋子中随机取出一个球,取出 球的可能性最大.
16.对于两个事件:事件1:任意掷一枚质地均匀的正方体骰子,掷出的点数是小于6;事件2:口袋中有除颜色外其他都完全相同的2个红球和1个白球,从中摸出2个球.其中至少一个是红球;其中必然事件的是事件 .
17.太阳从西边升起,这个事件是 发生的.(填“可能”、“不可能”或“必然”)
三、解答题
18.计算下列事件发生的概率并将你算出的概率标在下图中.(标序号)
(1)十五的月亮就像一个弯弯细勾;
(2)正常情况下,气温低于零摄氏度,水会结冰;
(3)任意掷一枚六面分别写有、、、、、的均匀骰子,“”朝上;
(4)从装有个红球,个白球,个黄球的口袋中任取一个球,恰好是白球(这些球除颜色外完全相同).
19.判断下列事件哪些是必然事件,哪些是不确定事件,哪些是不可能事件?
事件1:三条边对应相等的两个三角形全等
事件2:三个角对应相等的两个三角形全等
事件3:有两边和其中一边上的中线对应相等的两个三角形全等
事件4:有两边和其中一边的对角对应相等的两个三角形全等
事件5:有两角和其中一角的对边对应相等的两个三角形全等
20.对于事件4,现在我们通过画图来说明.例如,已知∠α和线段a,b.用直尺和圆规作△ABC,使得∠C=∠α,AC=b,AB=a
21.世界杯决赛分成8个小组,每小组4个队,小组进行单循环(每个队都与该小组的其他队比赛一场)比赛,选出2个队进入16强,胜一场得3分,平一场得1分,负一场得0分.
(1)求每小组共比赛多少场?
(2)在小组比赛中,现有一队得到6分,该队出线是一个确定事件,还是不确定事件?
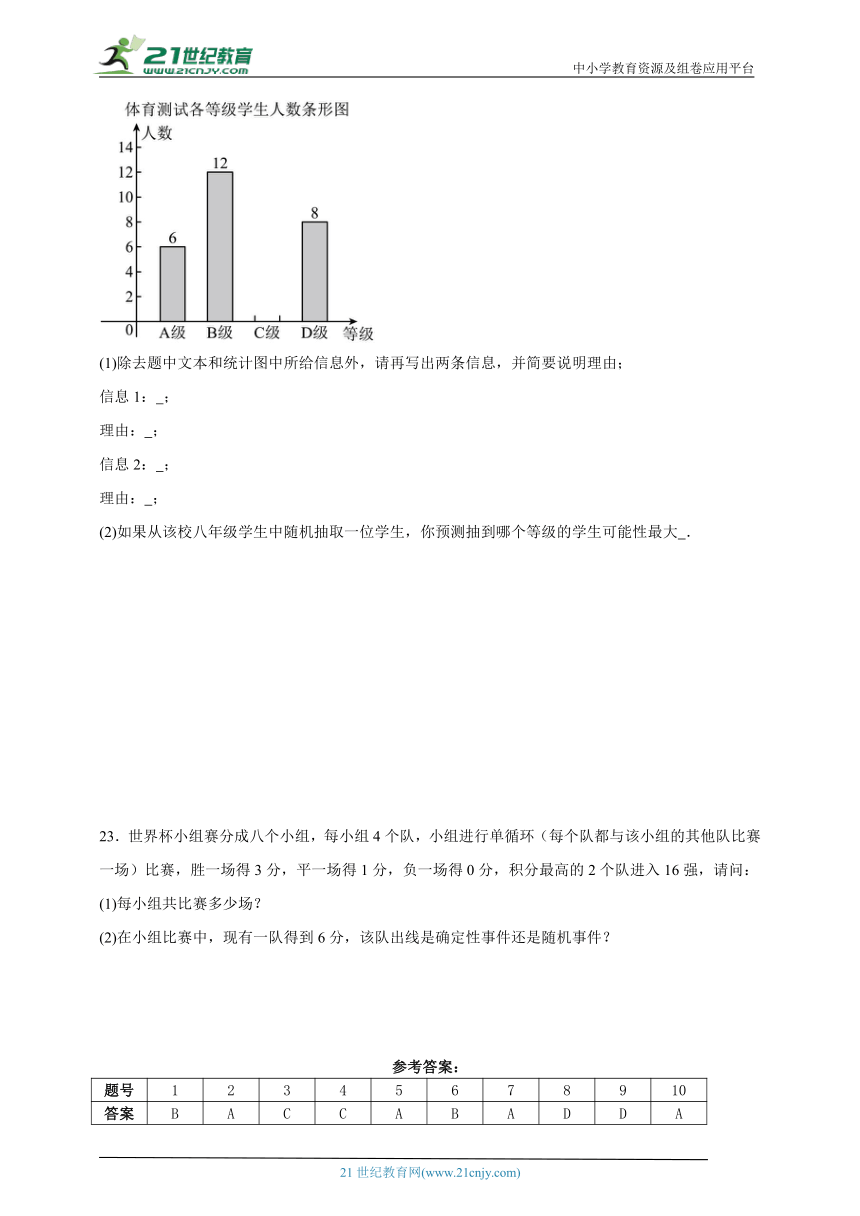
22.某学校为了解在校生的体能素质情况,从全体八年级学生中随机抽取部分学生进行了一次体育科目测试(把测试结果分为四个等级:A级:优秀,B级:良好,C级:及格,D级:不及格),其中B级占30%.解答下列问题:
(1)除去题中文本和统计图中所给信息外,请再写出两条信息,并简要说明理由;
信息1: ;
理由: ;
信息2: ;
理由: ;
(2)如果从该校八年级学生中随机抽取一位学生,你预测抽到哪个等级的学生可能性最大 .
23.世界杯小组赛分成八个小组,每小组4个队,小组进行单循环(每个队都与该小组的其他队比赛一场)比赛,胜一场得3分,平一场得1分,负一场得0分,积分最高的2个队进入16强,请问:
(1)每小组共比赛多少场?
(2)在小组比赛中,现有一队得到6分,该队出线是确定性事件还是随机事件?
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C C A B A D D A
题号 11 12
答案 A B
1.B
【分析】根据事件的分类及概念判断即可.
【详解】解:①投掷一枚硬币,正面朝上,是随机事件;
②方程两根之积等于,是必然事件,属于确定事件;
③经过红绿灯的十字路口,红绿灯为红灯,是随机事件;
④地球自转,是必然事件,属于确定事件;
⑤在篮球比赛中,弱队战胜强队,是随机事件;
故选:B.
【点睛】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.掌握事件的分类及概念是解题的关键.
2.A
【分析】分别求出甲、乙两人获胜的概率,再比较大小即可.
【详解】如图所示,
,
由图可知,甲胜的概率为:,
乙胜的概率为:,
∵,
∴甲获胜的可能性大.
故答案选:A.
【点睛】本题考查的知识点是可能性的大小, 解题的关键是熟练的掌握可能性的大小.
3.C
【分析】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.根据事件发生的可能性大小判断.
【详解】解:A、一个三角形的内角和为,是不可能事件,不符合题意;
B、掷一枚骰子,向上一面点数大于0,是必然事件,不符合题意;
C、经过有交通信号灯的路口,遇到红灯,是随机事件,符合题意;
D、3人分成两组一定有2人分在一组,是必然事件,不符合题意;
故选:C.
4.C
【分析】根据事件发生的可能性大小判断.
【详解】A、两张卡片的数字之和等于1,是不可能事件;
B、两张卡片的数字之和大于1,是必然事件;
C、两张卡片的数字之和等于12,是随机事件;
D、两张卡片的数字之和大于12,是不可能事件;
故选:C.
【点睛】本题考查的是必然事件、不可能事件、随机事件的概念。必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
5.A
【分析】根据事件发生的可能性大小判断相应事件的类型.
【详解】解:A,水中捞月是不可能事件;
B、守株待兔是随机事件;
C、水涨船高是必然事件;
D、水滴石穿是必然事件;
故选:A.
【点睛】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
6.B
【分析】本题主要考查了事件的分类,在一定条件下,一定会发生的事件叫做必然事件,据此判断求解即可.
【详解】解:打开电视机,它可能正在播广告,也坑不在播放广告,不是必然事件,不符合题意;
B、明天太阳从东方升起,是必然事件,符合题意;
C、某彩票的中奖机会是,买1张可能不会中奖,也坑会中奖,不是必然事件,不符合题意;
D、抛掷一枚硬币,可能正面朝上,也可能方面朝上,不是必然事件,不符合题意;
故选B.
7.A
【分析】利用随机事件以及必然事件的定义分析得出答案.
【详解】解:A、掷一枚普通的正方体骰子,掷得的点数不小于1,是必然事件,故此选项正确;
B、经过有交通信号灯的路口,遇到红灯,是随机事件,故此选项错误;
C、抛一枚普通的硬币,正面朝上,是随机事件,故此选项错误;
D、一年有367天,是不可能事件,故此选项错误;
故选A.
【点睛】本题主要考查了随机事件,正确把握各事件的定义是解题关键.
8.D
【分析】根据相应的概率判断出事件类型再进行解答即可.
【详解】解:“抛一枚硬币正面朝上的概率是”,说明此事件为随机事件,抛硬币次可能有次出现正面朝上;
彩票中奖的概率是”,说明此事件为随机事件,表示买张彩票会有中将的可能性.所以两种说法都错误.
故选:D.
【点睛】本题主要考查事件与概率的关系,解答此题要明确事件类型和概率的关系:
,表示事件为不可能事件,不会发生;
,表示事件为必然事件,一定发生;
,表示事件为随机事件,可能发生,也可能不发生.
9.D
【分析】根据事件发生的可能性大小判断即可.
【详解】解:A、购买两张彩票,一定中奖,是随机事件,不符合题意;
B、打开电视,正在播放新闻联播,是随机事件,不符合题意;
C、抛掷一枚硬币,正面向上,是随机事件,不符合题意;
D、三角形三个内角和为,是必然事件,符合题意;
故选:D.
【点睛】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
10.A
【分析】根据事件发生的可能性大小判断相应事件的类型即可.
【详解】∵5+12>13,
∴用长分别为5cm、12cm、13cm的三条线段能构成三角形,
又∵52+122=132,
∴“用长分别为5cm、12cm、13cm的三条线段可以围成直角三角形”这一事件是必然事件,
故选A.
【点睛】本题考查了随机事件,解决本题需要正确理解必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.本题也考查了三角形三条边的关系及勾股定理的逆定理.
11.A
【分析】根据事件发生的可能性大小判断相应事件的类型即可.
【详解】解:A、实数,则,是必然事件,符合题意;
B、我们班的同学将会有人成为航天员,是随机事件,不符合题意;
C、打开电视,正在播放新闻,是随机事件,不符合题意;
D、新疆的冬天不下雪,是随机事件,不符合题意;
故选:A.
【点睛】本题考查的是必然事件、不可能事件、随机事件的概念,解题的关键是掌握必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
12.B
【分析】根据三角形内角和定理,随机事件,必然事件,不可能事件的特点,即可解答.
【详解】解:A、通常温度降到以下,纯净的水结冰,是必然事件,故A不符合题意;
B、随意翻到一本书的某页,这页的页码是奇数,是随机事件,故B符合题意;
C、明天太阳从东方升起,是必然事件,故C不符合题意;
D、任意画一个三角形,其内角和是,是不可能事件,故D不符合题意;
故选:B.
【点睛】本题考查了三角形内角和定理,随机事件;熟练掌握随机事件,必然事件,不可能事件的特点是解题的关键.
13.②
【分析】根据不可能事件的定义进行求解即可:在一定条件下,不可能发生的事件是不可能事件.
【详解】解:①通常加热到 100℃,水沸腾,是必然事件,不符合题意;
②在平面上,任意画一个三角形,其内角和小于180°是不可能事件,符合题意;
故答案为:②
【点睛】本题主要考查了事件的分类,熟知不可能事件的定义是解题的关键.
14.必然事件
【分析】根据事件的分类特点解答即可.
【详解】解:不透明的袋子中有除颜色外完全相同的4个红球和2个绿球,从袋子中随机摸出3个球,至少有1个红球是必然事件,
故答案为:必然事件.
【点睛】此题考查事件分类,正确掌握必然事件,随机事件及不可能事件的定义是解题的关键.
15.红
【分析】根据题意得到相应的可能性,比较即可.
【详解】解:摸到红球的可能性为,摸到黄球的可能性为,摸到白球的可能性为,
所以摸到红球的可能性最大,
故答案为:红.
【点睛】本题考查的是可能性大小的判断,解决这类题目要注意具体情况具体对待.用到的知识点为:可能性等于所求情况数与总情况数之比.
16.2
【分析】根据事件发生的可能性判断即可;
【详解】解:事件1:正方体骰子有一面的数字为6,不小于6,所以事件为随机事件;
事件2:根据口袋中球的种类与个数可得,摸出2个球的可能情况为:2个红球,1红1白,所以至少一个红球是必然事件;
故答案为:2
【点睛】本题考查了事件可能性的判断,准确判断每个事件的可能性是解题关键.
17.不可能
【分析】根据不确定事件、不可能事件和必然事件的概念,即可解答.
必然事件:在一定条件下必然会发生的事件.
不可能事件:在一定条件下必然不会发生的事件.
不确定事件(或随机事件):在一定条件下可能发生,也可能不发生的事件.
【详解】太阳从西边升起,这个事件是不可能发生的.
故答案为不可能.
【点睛】本题考查不可能事件,必然事件,随机事件(不确定事件),解决这类问题的关键是理解不确定事件、不可能事件以及必然事件的概念.
18.(1)0,标序号见解析
(2)1,标序号见解析
(3),标序号见解析
(4),标序号见解析
【分析】根据随机事件的概率问题,正确理解概率的性质就能很快的得到答案.
【详解】(1)解:十五的月亮就像一个弯弯细勾,不可能发生,故概率为0;
(2)正常情况下,气温低于零摄氏度,水会结冰,一定发生,故概率为1;
(3)任意掷一枚六面分别写有1、2、3、4、5、6的均匀骰子,“3”朝上的概率为;
(4)从装有6个红球,20个白球,4个黄球的口袋中任取一个球,恰好是白球的概率为.
【点睛】本题主要考查了随机事件的概率问题,难度适中.
见解析.
【详解】本题考查的事件可能性的大小和尺规图.
答:(1)1,3,5是必然事件,2,4是不确定事件 (4分,选错一个扣一分)
(2)已知∠α和线段a,b.用直尺和圆规作△ABC,使得∠C=∠α,AC=b,AB=a
有两种情况,每个图得2分
22.(1)每小组共比赛6场
(2)该队出线是一个不确定事件
【分析】(1)每个小组有4个队,每队要和其余的3个队进行比赛,故要比赛场,而每两队之间只比赛一场,因此再除以2可完成解答;
(2)结合(1)的结论,先求出每组的最高得分,再求出剩下的分数,然后结合确定事件和随机事件的概念进行判断,即可完成解答.
【详解】(1)(场)
答:每小组共比赛6场.
(2)因为总共有6场比赛,
每场比赛最多可得3分,
则6场比赛最多共有分,
现有一队得6分,
还剩下12分,
则还有可能有2个队同时得6分,
故不能确保该队出线,因此该队出线是一个不确定事件.
【点睛】此题考查了随机事件,掌握不可能事件,必然事件,随机事件的概念是解题的关键.
23.(1)信息1: 总人数40人;理由见解析;信息2:C级人数为14人;理由见解析;
(2)C级
【分析】本题考查的是条形统计图的综合运用,读懂统计图,从统计图中得到必要的信息是解决问题的关键.
(1)信息1:根据B级的人数除以B级所占的百分比,可得抽测的人数;
信息2:用总人数分别减去A级,B级,D级得到C级人数;
(2)分别求出A级,C级,D级各级人数在总人数中的百分比和B级所占百分比进行比较即可.
【详解】(1)信息1:本次抽样测试的学生人数是40;
本次抽样测试的学生人数是(人),
故答案为:40;
信息2:C级人数为14人,
C级的人数为:(人);
故答案为:14;
(2)由(1)可知A级可能性为:
,
C级可能性为:
;
D级可能性为:
,
∴
∴抽到C级的学生可能性最大.
故答案为:C级.
24.(1)每小组共比赛6场;
(2)该队出线是一个随机事件.
【分析】(1)每个小组有4个队,每队要和其余的3个队进行比赛,故要比赛场,而每两队之间只比赛一场,因此再除以2可完成解答;
(2)结合(1)的结论,先求出每组的最高得分,再求出剩下的分数,然后结合确定事件和随机事件的概念进行判断,即可完成解答.
【详解】(1)解:(场)
答:每小组共比赛6场;
(2)解:因为总共有6场比赛,
每场比赛最多可得3分,
则6场比赛最多共有分,
现有一队得6分,
还剩下12分,
则还有可能有2个队同时得6分,
故不能确保该队出线,因此该队出线是一个随机事件.
【点睛】此题考查了随机事件,掌握不可能事件,必然事件,随机事件的概念是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第十三章事件与可能性
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列事件中,属于确定事件的有( )个.
①投掷一枚硬币,正面朝上;
②方程两根之积等于;
③经过红绿灯的十字路口,红绿灯为红灯;
④地球自转;
⑤在篮球比赛中,弱队战胜强队.
A.1 B.2 C.3 D.4
2.甲、乙两人做掷骰子游戏,规定:一人掷一次,若两人所掷骰子的点数和大于6,则甲胜;反之,乙胜.则甲、乙两人中( )
A.甲获胜的可能最大 B.乙获胜的可能最大
C.甲、乙获胜的可能一样大 D.由于是随机事件,因此无法估计
3.下列事件,是随机事件的是( )
A.一个三角形的内角和为 B.掷一枚股子,向上一面点数大于0
C.经过有交通信号灯的路口,遇到红灯 D.3人分成两组一定有2人分在一组
4.有六张背面完全相同的卡片,正面分别标有数字,从中分别抽取两张(放回), 则下列事件为随机事件的是( )
A.两张卡片的数字之和等于 B.两张卡片的数字之和大于
C.两张卡片的数字之和等于 D.两张卡片的数字之和大于
5.下列成语中,表示不可能事件的是( )
A.水中捞月 B.守株待兔 C.水涨船高 D.水滴石穿
6.下列事件为必然事件的是( )
A.打开电视机,它正在播广告 B.明天太阳从东方升起
C.某彩票的中奖机会是,买1张一定不会中奖 D.抛掷一枚硬币,一定正面朝上
7.下列事件为必然事件的是( ).
A.抛掷一枚普通的正方体骰子,掷得的点数不小于1
B.经过有交通信号灯的路口,遇到红灯
C.抛一枚普通的硬币,正面朝上
D.一年有367天
8.下列两个说法:
“抛一枚硬币正面朝上的概率是”表示抛硬币次必有次出现正面朝上;
“彩票中奖的概率是”表示买张彩票一定会中奖.
其中( )
A.都正确 B.只有正确 C.只有正确 D.两个说法都错误
9.下列事件为必然事件的是( )
A.购买两张彩票,一定中奖
B.打开电视,正在播放新闻联播
C.抛掷一枚硬币,正面向上
D.三角形三个内角和为
10.“用长分别为5cm、12cm、13cm的三条线段可以围成直角三角形”这一事件是( )
A.必然事件 B.不可能事件 C.随机事件 D.以上都不是
11.下列事件属于必然事件的是( )
A.实数a<0,则2a<0
B.我们班的同学将会有人成为航天员
C.打开电视,正在播放新闻
D.新疆的冬天不下雪
12.下列事件中,是随机事件的是( )
A.通常温度降到以下,纯净的水结冰
B.随意翻到一本书的某页,这页的页码是奇数
C.明天太阳从东方升起
D.任意画一个三角形,其内角和是
二、填空题
13.下列事件,①通常加热到 100℃,水沸腾;②在平面上,任意画一个三角形,其内角和小于 180°.其中是不可能事件的是 (只填写序号即可)
14.不透明的袋子中有除颜色外完全相同的4个红球和2个绿球,从袋子中随机摸出3个球,至少有1个红球是 .(填“随机事件”,“必然事件”或“不可能事件”)
15.一个不透明的袋子里装有3个红球,2个黄球,1个白球,这些球除颜色外无其他差别,从袋子中随机取出一个球,取出 球的可能性最大.
16.对于两个事件:事件1:任意掷一枚质地均匀的正方体骰子,掷出的点数是小于6;事件2:口袋中有除颜色外其他都完全相同的2个红球和1个白球,从中摸出2个球.其中至少一个是红球;其中必然事件的是事件 .
17.太阳从西边升起,这个事件是 发生的.(填“可能”、“不可能”或“必然”)
三、解答题
18.计算下列事件发生的概率并将你算出的概率标在下图中.(标序号)
(1)十五的月亮就像一个弯弯细勾;
(2)正常情况下,气温低于零摄氏度,水会结冰;
(3)任意掷一枚六面分别写有、、、、、的均匀骰子,“”朝上;
(4)从装有个红球,个白球,个黄球的口袋中任取一个球,恰好是白球(这些球除颜色外完全相同).
19.判断下列事件哪些是必然事件,哪些是不确定事件,哪些是不可能事件?
事件1:三条边对应相等的两个三角形全等
事件2:三个角对应相等的两个三角形全等
事件3:有两边和其中一边上的中线对应相等的两个三角形全等
事件4:有两边和其中一边的对角对应相等的两个三角形全等
事件5:有两角和其中一角的对边对应相等的两个三角形全等
20.对于事件4,现在我们通过画图来说明.例如,已知∠α和线段a,b.用直尺和圆规作△ABC,使得∠C=∠α,AC=b,AB=a
21.世界杯决赛分成8个小组,每小组4个队,小组进行单循环(每个队都与该小组的其他队比赛一场)比赛,选出2个队进入16强,胜一场得3分,平一场得1分,负一场得0分.
(1)求每小组共比赛多少场?
(2)在小组比赛中,现有一队得到6分,该队出线是一个确定事件,还是不确定事件?
22.某学校为了解在校生的体能素质情况,从全体八年级学生中随机抽取部分学生进行了一次体育科目测试(把测试结果分为四个等级:A级:优秀,B级:良好,C级:及格,D级:不及格),其中B级占30%.解答下列问题:
(1)除去题中文本和统计图中所给信息外,请再写出两条信息,并简要说明理由;
信息1: ;
理由: ;
信息2: ;
理由: ;
(2)如果从该校八年级学生中随机抽取一位学生,你预测抽到哪个等级的学生可能性最大 .
23.世界杯小组赛分成八个小组,每小组4个队,小组进行单循环(每个队都与该小组的其他队比赛一场)比赛,胜一场得3分,平一场得1分,负一场得0分,积分最高的2个队进入16强,请问:
(1)每小组共比赛多少场?
(2)在小组比赛中,现有一队得到6分,该队出线是确定性事件还是随机事件?
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C C A B A D D A
题号 11 12
答案 A B
1.B
【分析】根据事件的分类及概念判断即可.
【详解】解:①投掷一枚硬币,正面朝上,是随机事件;
②方程两根之积等于,是必然事件,属于确定事件;
③经过红绿灯的十字路口,红绿灯为红灯,是随机事件;
④地球自转,是必然事件,属于确定事件;
⑤在篮球比赛中,弱队战胜强队,是随机事件;
故选:B.
【点睛】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.掌握事件的分类及概念是解题的关键.
2.A
【分析】分别求出甲、乙两人获胜的概率,再比较大小即可.
【详解】如图所示,
,
由图可知,甲胜的概率为:,
乙胜的概率为:,
∵,
∴甲获胜的可能性大.
故答案选:A.
【点睛】本题考查的知识点是可能性的大小, 解题的关键是熟练的掌握可能性的大小.
3.C
【分析】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.根据事件发生的可能性大小判断.
【详解】解:A、一个三角形的内角和为,是不可能事件,不符合题意;
B、掷一枚骰子,向上一面点数大于0,是必然事件,不符合题意;
C、经过有交通信号灯的路口,遇到红灯,是随机事件,符合题意;
D、3人分成两组一定有2人分在一组,是必然事件,不符合题意;
故选:C.
4.C
【分析】根据事件发生的可能性大小判断.
【详解】A、两张卡片的数字之和等于1,是不可能事件;
B、两张卡片的数字之和大于1,是必然事件;
C、两张卡片的数字之和等于12,是随机事件;
D、两张卡片的数字之和大于12,是不可能事件;
故选:C.
【点睛】本题考查的是必然事件、不可能事件、随机事件的概念。必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
5.A
【分析】根据事件发生的可能性大小判断相应事件的类型.
【详解】解:A,水中捞月是不可能事件;
B、守株待兔是随机事件;
C、水涨船高是必然事件;
D、水滴石穿是必然事件;
故选:A.
【点睛】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
6.B
【分析】本题主要考查了事件的分类,在一定条件下,一定会发生的事件叫做必然事件,据此判断求解即可.
【详解】解:打开电视机,它可能正在播广告,也坑不在播放广告,不是必然事件,不符合题意;
B、明天太阳从东方升起,是必然事件,符合题意;
C、某彩票的中奖机会是,买1张可能不会中奖,也坑会中奖,不是必然事件,不符合题意;
D、抛掷一枚硬币,可能正面朝上,也可能方面朝上,不是必然事件,不符合题意;
故选B.
7.A
【分析】利用随机事件以及必然事件的定义分析得出答案.
【详解】解:A、掷一枚普通的正方体骰子,掷得的点数不小于1,是必然事件,故此选项正确;
B、经过有交通信号灯的路口,遇到红灯,是随机事件,故此选项错误;
C、抛一枚普通的硬币,正面朝上,是随机事件,故此选项错误;
D、一年有367天,是不可能事件,故此选项错误;
故选A.
【点睛】本题主要考查了随机事件,正确把握各事件的定义是解题关键.
8.D
【分析】根据相应的概率判断出事件类型再进行解答即可.
【详解】解:“抛一枚硬币正面朝上的概率是”,说明此事件为随机事件,抛硬币次可能有次出现正面朝上;
彩票中奖的概率是”,说明此事件为随机事件,表示买张彩票会有中将的可能性.所以两种说法都错误.
故选:D.
【点睛】本题主要考查事件与概率的关系,解答此题要明确事件类型和概率的关系:
,表示事件为不可能事件,不会发生;
,表示事件为必然事件,一定发生;
,表示事件为随机事件,可能发生,也可能不发生.
9.D
【分析】根据事件发生的可能性大小判断即可.
【详解】解:A、购买两张彩票,一定中奖,是随机事件,不符合题意;
B、打开电视,正在播放新闻联播,是随机事件,不符合题意;
C、抛掷一枚硬币,正面向上,是随机事件,不符合题意;
D、三角形三个内角和为,是必然事件,符合题意;
故选:D.
【点睛】本题考查的是必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
10.A
【分析】根据事件发生的可能性大小判断相应事件的类型即可.
【详解】∵5+12>13,
∴用长分别为5cm、12cm、13cm的三条线段能构成三角形,
又∵52+122=132,
∴“用长分别为5cm、12cm、13cm的三条线段可以围成直角三角形”这一事件是必然事件,
故选A.
【点睛】本题考查了随机事件,解决本题需要正确理解必然事件、不可能事件、随机事件的概念.必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.本题也考查了三角形三条边的关系及勾股定理的逆定理.
11.A
【分析】根据事件发生的可能性大小判断相应事件的类型即可.
【详解】解:A、实数,则,是必然事件,符合题意;
B、我们班的同学将会有人成为航天员,是随机事件,不符合题意;
C、打开电视,正在播放新闻,是随机事件,不符合题意;
D、新疆的冬天不下雪,是随机事件,不符合题意;
故选:A.
【点睛】本题考查的是必然事件、不可能事件、随机事件的概念,解题的关键是掌握必然事件指在一定条件下,一定发生的事件.不可能事件是指在一定条件下,一定不发生的事件,不确定事件即随机事件是指在一定条件下,可能发生也可能不发生的事件.
12.B
【分析】根据三角形内角和定理,随机事件,必然事件,不可能事件的特点,即可解答.
【详解】解:A、通常温度降到以下,纯净的水结冰,是必然事件,故A不符合题意;
B、随意翻到一本书的某页,这页的页码是奇数,是随机事件,故B符合题意;
C、明天太阳从东方升起,是必然事件,故C不符合题意;
D、任意画一个三角形,其内角和是,是不可能事件,故D不符合题意;
故选:B.
【点睛】本题考查了三角形内角和定理,随机事件;熟练掌握随机事件,必然事件,不可能事件的特点是解题的关键.
13.②
【分析】根据不可能事件的定义进行求解即可:在一定条件下,不可能发生的事件是不可能事件.
【详解】解:①通常加热到 100℃,水沸腾,是必然事件,不符合题意;
②在平面上,任意画一个三角形,其内角和小于180°是不可能事件,符合题意;
故答案为:②
【点睛】本题主要考查了事件的分类,熟知不可能事件的定义是解题的关键.
14.必然事件
【分析】根据事件的分类特点解答即可.
【详解】解:不透明的袋子中有除颜色外完全相同的4个红球和2个绿球,从袋子中随机摸出3个球,至少有1个红球是必然事件,
故答案为:必然事件.
【点睛】此题考查事件分类,正确掌握必然事件,随机事件及不可能事件的定义是解题的关键.
15.红
【分析】根据题意得到相应的可能性,比较即可.
【详解】解:摸到红球的可能性为,摸到黄球的可能性为,摸到白球的可能性为,
所以摸到红球的可能性最大,
故答案为:红.
【点睛】本题考查的是可能性大小的判断,解决这类题目要注意具体情况具体对待.用到的知识点为:可能性等于所求情况数与总情况数之比.
16.2
【分析】根据事件发生的可能性判断即可;
【详解】解:事件1:正方体骰子有一面的数字为6,不小于6,所以事件为随机事件;
事件2:根据口袋中球的种类与个数可得,摸出2个球的可能情况为:2个红球,1红1白,所以至少一个红球是必然事件;
故答案为:2
【点睛】本题考查了事件可能性的判断,准确判断每个事件的可能性是解题关键.
17.不可能
【分析】根据不确定事件、不可能事件和必然事件的概念,即可解答.
必然事件:在一定条件下必然会发生的事件.
不可能事件:在一定条件下必然不会发生的事件.
不确定事件(或随机事件):在一定条件下可能发生,也可能不发生的事件.
【详解】太阳从西边升起,这个事件是不可能发生的.
故答案为不可能.
【点睛】本题考查不可能事件,必然事件,随机事件(不确定事件),解决这类问题的关键是理解不确定事件、不可能事件以及必然事件的概念.
18.(1)0,标序号见解析
(2)1,标序号见解析
(3),标序号见解析
(4),标序号见解析
【分析】根据随机事件的概率问题,正确理解概率的性质就能很快的得到答案.
【详解】(1)解:十五的月亮就像一个弯弯细勾,不可能发生,故概率为0;
(2)正常情况下,气温低于零摄氏度,水会结冰,一定发生,故概率为1;
(3)任意掷一枚六面分别写有1、2、3、4、5、6的均匀骰子,“3”朝上的概率为;
(4)从装有6个红球,20个白球,4个黄球的口袋中任取一个球,恰好是白球的概率为.
【点睛】本题主要考查了随机事件的概率问题,难度适中.
见解析.
【详解】本题考查的事件可能性的大小和尺规图.
答:(1)1,3,5是必然事件,2,4是不确定事件 (4分,选错一个扣一分)
(2)已知∠α和线段a,b.用直尺和圆规作△ABC,使得∠C=∠α,AC=b,AB=a
有两种情况,每个图得2分
22.(1)每小组共比赛6场
(2)该队出线是一个不确定事件
【分析】(1)每个小组有4个队,每队要和其余的3个队进行比赛,故要比赛场,而每两队之间只比赛一场,因此再除以2可完成解答;
(2)结合(1)的结论,先求出每组的最高得分,再求出剩下的分数,然后结合确定事件和随机事件的概念进行判断,即可完成解答.
【详解】(1)(场)
答:每小组共比赛6场.
(2)因为总共有6场比赛,
每场比赛最多可得3分,
则6场比赛最多共有分,
现有一队得6分,
还剩下12分,
则还有可能有2个队同时得6分,
故不能确保该队出线,因此该队出线是一个不确定事件.
【点睛】此题考查了随机事件,掌握不可能事件,必然事件,随机事件的概念是解题的关键.
23.(1)信息1: 总人数40人;理由见解析;信息2:C级人数为14人;理由见解析;
(2)C级
【分析】本题考查的是条形统计图的综合运用,读懂统计图,从统计图中得到必要的信息是解决问题的关键.
(1)信息1:根据B级的人数除以B级所占的百分比,可得抽测的人数;
信息2:用总人数分别减去A级,B级,D级得到C级人数;
(2)分别求出A级,C级,D级各级人数在总人数中的百分比和B级所占百分比进行比较即可.
【详解】(1)信息1:本次抽样测试的学生人数是40;
本次抽样测试的学生人数是(人),
故答案为:40;
信息2:C级人数为14人,
C级的人数为:(人);
故答案为:14;
(2)由(1)可知A级可能性为:
,
C级可能性为:
;
D级可能性为:
,
∴
∴抽到C级的学生可能性最大.
故答案为:C级.
24.(1)每小组共比赛6场;
(2)该队出线是一个随机事件.
【分析】(1)每个小组有4个队,每队要和其余的3个队进行比赛,故要比赛场,而每两队之间只比赛一场,因此再除以2可完成解答;
(2)结合(1)的结论,先求出每组的最高得分,再求出剩下的分数,然后结合确定事件和随机事件的概念进行判断,即可完成解答.
【详解】(1)解:(场)
答:每小组共比赛6场;
(2)解:因为总共有6场比赛,
每场比赛最多可得3分,
则6场比赛最多共有分,
现有一队得6分,
还剩下12分,
则还有可能有2个队同时得6分,
故不能确保该队出线,因此该队出线是一个随机事件.
【点睛】此题考查了随机事件,掌握不可能事件,必然事件,随机事件的概念是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第十章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的乘除法
- 10.4 分式的加减法
- 10.5 可化为一元一次方程的分式方程及其应用
- 第十一章 实数和二次根式
- 11.1 平方根
- 11.2 立方根
- 11.3 用科学计算器开方
- 11.4 无理数与实数
- 11.5 二次根式及其性质
- 11.6 二次根式的乘除法
- 11.7 二次根式的加减法
- 第十二章 三角形
- 12.1 三角形
- 12.2 三角形的性质
- 12.3 三角形中的主要线段
- 12.4 全等三角形
- 12.5 全等三角形的判定
- 12.6 等腰三角形
- 12.7 直角三角形
- 12.8 基本作图
- 12.9 逆命题 、逆定理
- 12.10 轴对称和轴对称图形
- 12.11 勾股定理
- 12.12 勾股定理的逆定理
- 第十三章 事件与可能性
- 13.1 必然事件与随机事件
- 13.2 随机事件发生的可能性
- 13.3 求简单随机事件发生的可能性的大小
