第十八章相似形同步练习（含解析）

中小学教育资源及组卷应用平台
第十八章相似形
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．如图，在中，，，则下列结论正确的是（ ）
A． B． C． D．
2．如图，D是等边△ABC边AB上的一点，且AD：DB＝2：3，现将△ABC折叠，使点C与D重合，折痕为EF，点E，F分别在AC和BC上，则CE：CF＝（　　）
A． B． C． D．
3．如图，在平行四边形中，对角线与相交于点O，，过点B作交于点E，若，则的长为（ ）

A． B． C．2 D．
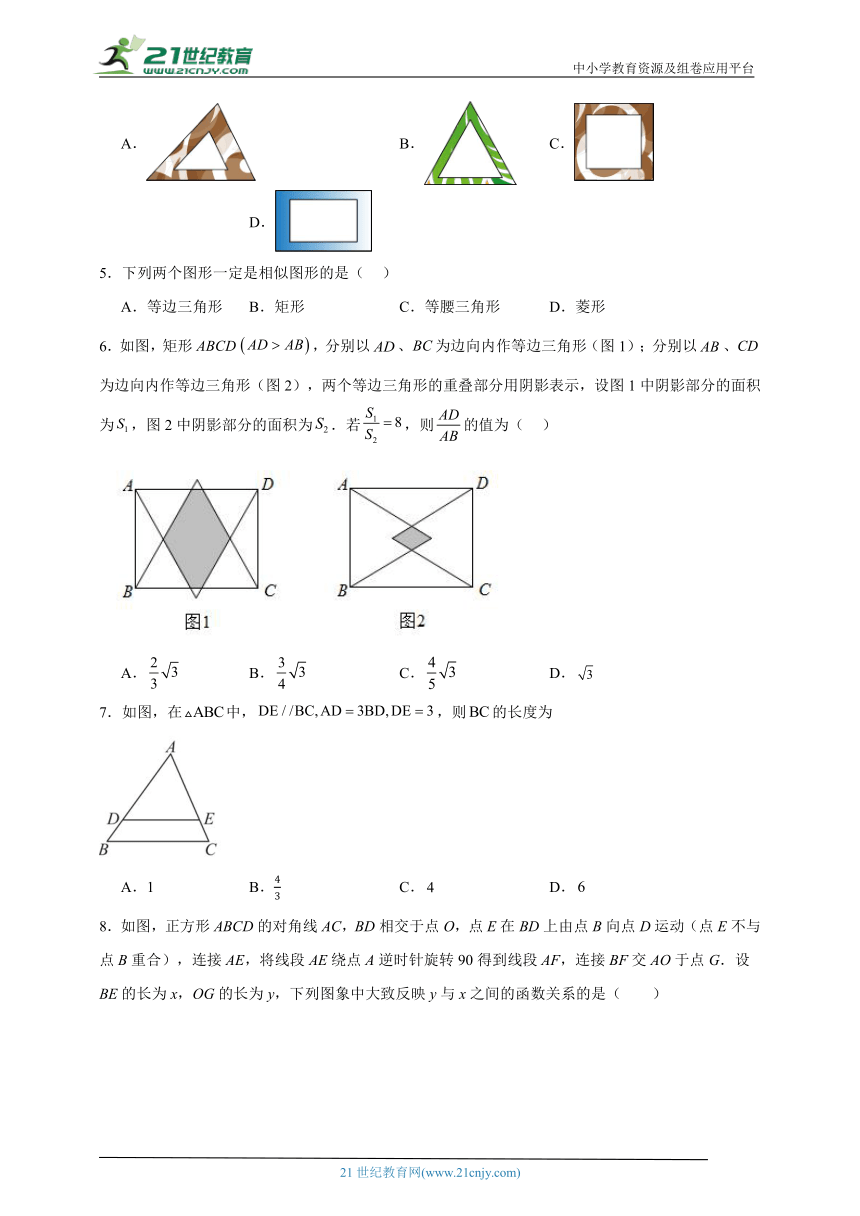
4．手工制作课上，小红利用一些花布的边角料，剪裁后装饰手工画，下面四个图案是她剪裁出的空心不等边三角形、等边三角形、正方形、矩形花边，其中，每个图案花边的宽度都相等，那么，每个图案中花边的内外边缘所围成的几何图形不一定相似的是（　　）
A． B． C． D．
5．下列两个图形一定是相似图形的是（ ）
A．等边三角形 B．矩形 C．等腰三角形 D．菱形
6．如图，矩形，分别以、为边向内作等边三角形（图1）；分别以、为边向内作等边三角形（图2），两个等边三角形的重叠部分用阴影表示，设图1中阴影部分的面积为，图2中阴影部分的面积为．若，则的值为（ ）
A． B． C． D．
7．如图，在中，，则的长度为
A．1 B． C． D．
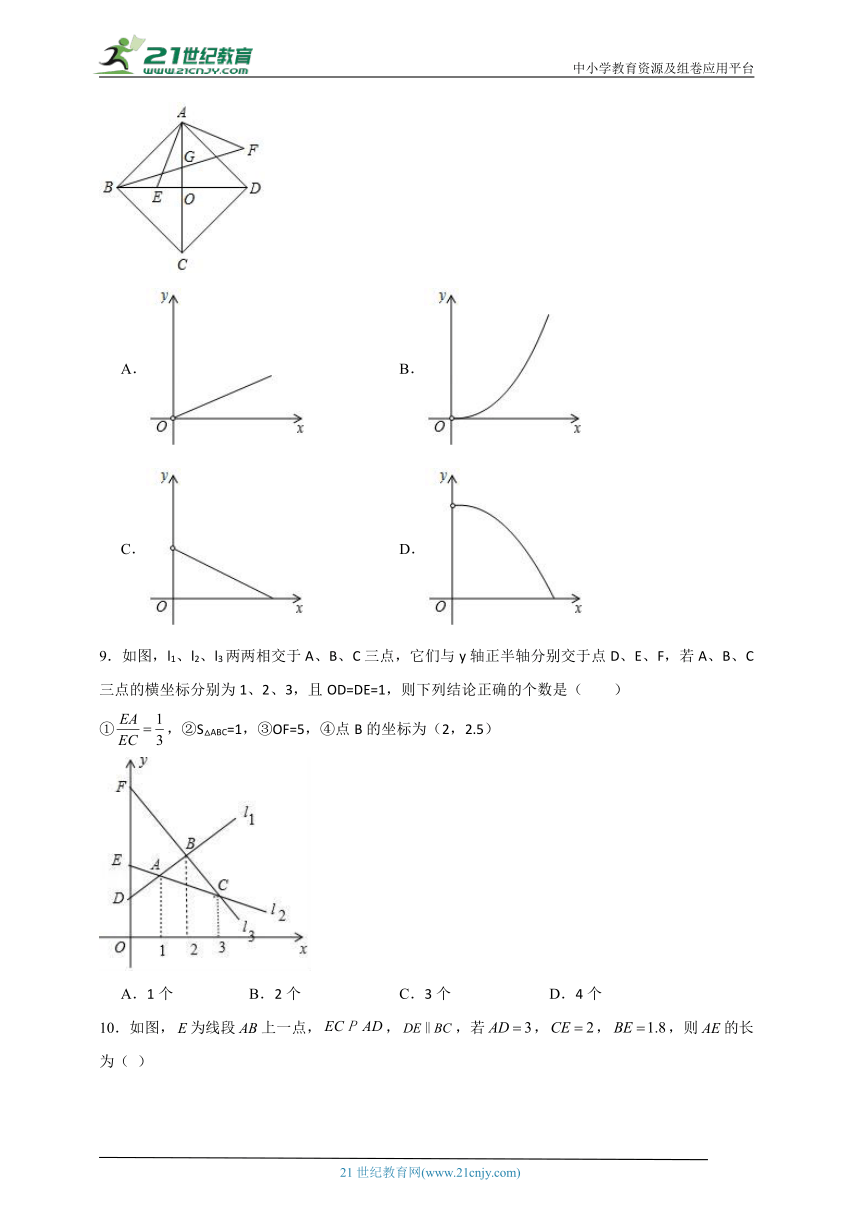
8．如图，正方形ABCD的对角线AC，BD相交于点O，点E在BD上由点B向点D运动（点E不与点B重合），连接AE，将线段AE绕点A逆时针旋转90得到线段AF，连接BF交AO于点G．设BE的长为x，OG的长为y，下列图象中大致反映y与x之间的函数关系的是（　　）
A． B．
C． D．
9．如图，l1、l2、l3两两相交于A、B、C三点，它们与y轴正半轴分别交于点D、E、F，若A、B、C三点的横坐标分别为1、2、3，且OD=DE=1，则下列结论正确的个数是（　　）
①，②S△ABC=1，③OF=5，④点B的坐标为（2，2.5）
A．1个 B．2个 C．3个 D．4个
10．如图，为线段上一点，，，若，，，则的长为（ ）
A．1.2 B．2.4 C．2.7 D．3
11．已知，与的面积比为，若，则的长为（ ）
A．1 B．2 C．4 D．8
12．如图，已知一组平行线，被直线m、n所截，交点分别为A、B、C和D、E、F，且，，，则是（ ）
A． B． C． D．
二、填空题
13．如图，在矩形中，，点E，F分别在边上，且，将矩形沿折叠后，点D，C分别落在处，延长交BC于点G．当A，，三点共线时，的面积是 ．

14．正五角星是一个非常优美的几何图形，在如图所示的正五角星中，以、、、、为顶点的多边形为正五边形，其余各点都是对角线的交点，下列4个结论：①，②，③，④．
请填写你认为正确的结论序号： ．
15．已知，则 ．
16．如图，已知点D、E分别在△ABC的边AB和AC上，且DE∥BC，S△AED︰S梯形EDBC＝1︰2，则AE︰AC的比值是 ．
17．如图，点P为矩形ABCD边AD上一点，点E、F分别为PB、PC的中点，若矩形ABCD的面积为5，那么△PEF的面积为 ．
三、解答题
18．为了测量校园水平地面上一棵树的高度，数学兴趣小组利用一根标杆、皮尺，设计如图所示的测量方案．已知测量同学眼睛A、标杆顶端F、树的顶端E在同一直线上，此同学眼睛距地面1．6米，标杆高为3．2米，且BC=2米，CD=6米，求树ED的高．
19．如图1，在矩形中，，，动点以每秒个单位长度的速度沿的路径运动，动点以每秒2个单位长度的速度沿的路径运动，当点到达点时，两者都停止运动．设运动时间为秒，点、的距离为．
(1)请直接写出关于的函数表达式并注明自变量的取值范围；
(2)在如图2所示的平面直角坐标系中画出函数的图象，并写出该函数的一条性质；
(3)结合函数图象，请直接写出当函数与上述函数的图像有两个交点时的取值范围．
20．如图，在正方形中，，点E，F分别在边，上，于点．若，求的长．
21．研学实践：“秋风楼”位于后土祠正殿后（位于古河东郡汾阴县，即今山西省万荣县西南），因楼上藏有汉武帝刘彻《秋风辞》碑而得名．因黄河淹没，曾于清代康熙、同治年间重修，现存建筑于同治九年（公元年）重建．某校组织研学活动，同学们来到秋风楼的所在地，利用测量工具等采集了秋风楼的相关数据．
数据采集：如图，是秋风楼顶部的一点，的长表示点到地面的距离，小康把长为米的标杆垂直立于地面点处，当秋风楼顶部和标杆的端点确定的直线交直线于点时，米；将标杆沿着的方向平移到点处，当秋风楼顶部和标杆的顶端确定的直线交直线于点时，测得米，米．
数据应用：已知图中各点都在同一平面内，根据上述数据，计算秋风楼顶部到地面的距离．
22．如图，为了求出海岛上的山峰的高度，在D处和F处树立标杆和，标杆的高都是20米，D，F两处相隔200米，并且，和在同一平面内．从标杆后退80米的G处，可以看到顶峰A和标杆顶端C在一条直线上；从标杆后退160米的H处，可以看到顶峰A和标杆顶端E在一条直线上．求山峰的高度及它和标杆的水平距离各是多少米？
23．在中，设，分别以，为底边向外作等腰和等腰，使．

(1)如图1，当时，则_________；
【探究证明】
(2)如图2，判断与的位置关系，并加以证明；
【求解感悟】
(3)如图3，连接，交内部于点，连接．
①若，则__________；
②求证：
③试说明：无论为何值，点都在的平分线上．
24．如图，E是正方形的边上的一点，于点F．求证：．
参考答案：
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D D A B C A C C
题号 11 12
答案 B B
1．B
【分析】本题考查相似三角形的判定及性质，由，，证明，再利用其性质得线段比例关系是解决问题的关键．
【详解】解：∵，，，
∴，
∴，
则，，
故选：B．
2．A
【分析】依据翻折变换的性质得到DE＝CE、CF＝DF；设AD＝2k，则DB＝3k；根据相似三角形的判定与性质即可解决问题．
【详解】解：设AD＝2k，则DB＝3k，
∵△ABC为等边三角形，
∴AB＝AC＝5k，∠A＝∠B＝∠C＝∠EDF＝60°，
∴∠EDA＋∠FDB＝120°，
又∵∠EDA＋∠AED＝120°，
∴∠FDB＝∠AED，
∴△AED∽△BDF，
由折叠得CE＝DE，CF＝DF，
∴△AED的周长为7k，△BDF的周长为8k，
∴△AED与△BDF的相似比为7：8，
∴CE：CF＝DE：DF＝7：8．
故选：A．
【点睛】主要考查了翻折变换的性质、相似三角形的判定和性质，解题的关键是利用相似三角形的周长之比等于相似比，学会根据条件用字母表示相应的线段长度．
3．D
【分析】先证出平行四边形是菱形，根据菱形的性质可得，利用勾股定理可得，再证出，利用相似三角形的性质求解即可得．
【详解】解：，
，
∵四边形是平行四边形，
平行四边形是菱形，
，
，
，
又，
，
，
，
，
，即，
解得，
故选：D．
【点睛】本题考查了等腰三角形的判定、菱形的判定与性质、勾股定理、相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解题关键．
4．D
【分析】根据相似图形的定义，结合图形，对选项一一分析，排除不符合要求答案．
【详解】解：A．形状相同，符合相似形的定义，对应角相等，所以三角形相似，故A选项不符合要求；
B．形状相同，符合相似形的定义，故B选项不符合要求；
C．形状相同，符合相似形的定义，故C选项不符合要求；
D．两个矩形，虽然四个角对应相等，但对应边不成比例，故D选项符合要求；
故选：D．
【点睛】本题考查的是相似形的定义，联系图形，即形状相同，大小不一定相同的图形叫做相似形．全等形是相似形的一个特例．
5．A
【分析】根据相似图形的定义：形状相同的图形称为相似图形进行分析即可．
【详解】解：A、两个等边三角形的对应边的比相等，对应角相等，故两个等边三角形一定相似，此选项符合题意；
B、两个矩形的对应角相等，但对应边的比不一定相等，故两个矩形不一定是相似图形，此选项不符合题意；
C、两个等腰三角形对应边的比不一定相等，对应角不一定相等，故两个等腰三角形不一定是相似图形，此选项不符合题意；
D、两个菱形的对应角不一定相等，对应边的比相等，故两个菱形不一定是相似图形，此选项不符合题意；
故选：A．
【点睛】本题考查了相似图形，解题的关键是掌握相似图形的定义．
6．B
【分析】将阴影部分分别分割成两个规则图形，图一可以分为两个梯形，图二可分成两个三角形，设设=m，令AB=1,则AD=m，利用相似求出图形面积，结合面积比即可求出．
【详解】
设=m，令AB=1,则AD=m，
∵两个正三角形以AD、BC为底，所得图形是对称图形，
∴EF所在直线平行AD与BC，
∴AM=BM=，
∵∠HBE=90°-60°=30°，
∴AH=，
∴ME=
根据对称性关系可知EF=m-2×=m-，HG=m-
∴梯形EFGH面积=
∴S1=，
同理根据图二可知
AK=，△ABR的高为，
∴△QPR的高为，
根据△QPR∽△ABR，
求得PQ=
∴三角形PQR面积=，
∴S2=，
∵，
整理得到：，
∴化简求得m=或（舍弃），
∴=，
故选：B．
【点睛】本题主要考查相似三角形、等边三角形有关知识，对知识的灵活运用要求较高，注重培养学生的分析问题和知识综合运用能力．
7．C
【分析】根据已知条件得到，根据相似三角形的判定和性质可得，即可得到结论．
【详解】解：∵，
∴，
∵DE∥BC，
∴△ADE∽△ABC，
,
∴,
∴BC=4.
故选：C．
【点睛】本题考查了相似三角形的判定与性质，熟悉相似基本图形掌握相似三角形的判定与性质是解题关键．
8．A
【分析】连接FD，证明△BAE≌△DAF，得到∠ADF=∠ABE=45°，FD=BE，再说明GO为△BDF的中位线，则 ，且x＞0，是在第一象限的一次函数图象．
【详解】连接FD，
∵∠BAE+∠EAD＝90°，∠FAD+∠EAD＝90°，
∴∠BAE＝∠FAD．
又BA＝DA，EA＝FA，
∴△BAE≌△DAF（SAS）．
∴∠ADF＝∠ABE＝45°，FD＝BE．
∴∠FDO＝45°+45°＝90°．
∵GO⊥BD，FD⊥BD，
∴GO∥FD．
∵O为BD中点，
∴GO为△BDF的中位线．
∴．
∴，且x＞0，是在第一象限的一次函数图象．
故选A．
【点睛】本题主要考查了动点问题的函数图象、全等三角形的判定和性质、中位线的性质定理，解题的关键是通过辅助线构造全等三角形而后转化线段．
9．C
【分析】①如图，由平行线等分线段定理（或分线段成比例定理）易得：；
②设过点B且与y轴平行的直线交AC于点G，则S△ABC=S△AGB+S△BCG，易得：S△AED＝，△AED∽△AGB且相似比=1，所以，△AED≌△AGB，所以，S△AGB＝，又易得G为AC中点，所以，S△AGB=S△BGC=，从而得结论；
③易知，BG=DE=1，又△BGC∽△FEC，列比例式可得结论；
④易知，点B的位置会随着点A在直线x=1上的位置变化而相应的发生变化，所以④错误．
【详解】解：①如图，∵OE∥AA'∥CC'，且OA'=1，OC'=3，
∴，
故 ①正确；
②设过点B且与y轴平行的直线交AC于点G（如图），则S△ABC=S△AGB+S△BCG，
∵DE=1，OA'=1，
∴S△AED=×1×1=，
∵OE∥AA'∥GB'，OA'=A'B'，
∴AE=AG，
∴△AED∽△AGB且相似比=1，
∴△AED≌△AGB，
∴S△ABG=，
同理得：G为AC中点，
∴S△ABG=S△BCG=，
∴S△ABC=1，
故 ②正确；
③由②知：△AED≌△AGB，
∴BG=DE=1，
∵BG∥EF，
∴△BGC∽△FEC，
∴，
∴EF=3．即OF=5，
故③正确；
④易知，点B的位置会随着点A在直线x=1上的位置变化而相应的发生变化，
故④错误；
故选C．
【点睛】本题考查了图形与坐标的性质、三角形的面积求法、相似三角形的性质和判定、平行线等分线段定理、函数图象交点等知识及综合应用知识、解决问题的能力．考查学生数形结合的数学思想方法．
10．C
【分析】根据平行线的性质和相似三角形的判定得出证得△DAE∽△CEB，再利用相似三角形的性质列出比例式，代入数值计算即可．
【详解】解：∵EC∥AD，DE∥BC，
∴∠A=∠CEA，∠AED=∠B，
∴△DAE∽△CEB，
∴，
∵，，，
∴，
∴AE=2.7，
故选：C．
【点睛】本题考查相似三角形的判定与性质、平行线的性质，熟练掌握相似三角形的判定与性质是解答的关键．
11．B
【分析】本题考查相似三角形的性质，根据相似三角形的面积比等于相似比的平方求解即可．
【详解】解：∵，
∴，
∵与的面积比为，，
∴，则（负值舍去），
故选：B．
12．B
【分析】本题考查了平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例．根据平行线分线段成比例定理得到，然后利用比例性质可求出的长即可．
【详解】解：∵，
∴，
即，
∴．
故选：B．
13．
【分析】本题主要考查矩形，折叠，相似三角形的综合，掌握矩形的性质，折叠的性质，三角形相似的判定和性质是解题的关键．
如图所示，根据折叠，可求出的长度，可知，求出的长度，在中，根据勾股定理可求出的长度，再证明，即可求解．
【详解】解∶矩形中，，
根据折叠可知，，，
，
在中，，
，
∴，
∴
∵，
，
，且，
，且，
，且，
，，
，
在中，设，
则， ，
∴，即，解得，，
∴，
，
∴， ，
，
，
，
．
故答案为：．
14．①②③
【分析】先讨论顶角为和的等腰三角形中的黄金分割关系，再在题中的所给图形中分析出顶角为和的等腰三角形，逐个判断即可．本题考查了正多边形与圆，准确掌握正多边形的相关性质及黄金分割的比例关系，并能准确的计算是本题的解题关键．
【详解】解：如图1，中，，，平分，
，，
和为相似的等腰三角形，
设，，
，
由相似得：，
（负值舍去），
点是线段的黄金分割点，
即：，，
，
；
如图2，中，，，，
，，
和为相似的等腰三角形，
设，，则，
由相似得：，
（负值舍去），
点是线段的黄金分割点，
即：，，
，
；
如图，连接、、、、，
五边形为正五边形，，
，
，
，故①正确；
易证：，，
和为相似的等腰三角形，
由图2得：，
，故②正确；
由题得和为相似的等腰三角形，
由图2得：，
，
，
，故③正确；
在中，，，
由图1得：，
即：，故④错误，
故答案为：①②③．
15．/
【分析】本题考查了比例的性质，设，则，代入代数式，即可求解．
【详解】解：∵，
∴，
∴，
故答案为：．
16．
【详解】试题分析：依题意可设
所以
所以
考点：相似三角形的性质
点评：主要教学目标是让学生会用三角形的相似解决一些实际问题；培养学生提出问题、解决问题的能力．
17．
【分析】先根据S矩形ABCD=5知S△PBC=S矩形ABCD=，再证△PEF∽△PBC得，即，据此可得答案．
【详解】∵矩形ABCD的面积为5，
∴S△PBC=S矩形ABCD=，
∵E、F分别是PB、PC的中点，
∴EF∥BC，且EF=BC，
∴△PEF∽△PBC，
∴，即，
∴S△PEF=，
故答案为．
【点睛】本题主要考查矩形的性质，解题的关键是掌握矩形的性质与相似三角形的判定与性质．
18．8米
【详解】试题分析：过A作AH垂直ED，垂足为H，交线段FC与G，根据题意得出 △AFG∽△AEH，从而求出EH的长度，根据ED=EH+HD得出答案.
试题解析：如图，过A作AH垂直ED，垂足为H，交线段FC与G,
由题知，FG//EH, △AFG∽△AEH，
又因为AG="BC=2,AH=BD=2+6=8,FG=FC-GC=3.2" -1.6=1.6， 所以，EH=6.4，
∴ED=EH+HD=6.4+1.6=8 树ED的高为8米
考点：相似三角形的应用.
19．(1)
(2)图象见解析，性质：当，y随x的增大而减小（答案不唯一）
(3)
【分析】此题考查了动点问题，一次函数的图象及性质，菱形的性质及等边三角形的判定和性质：
（1）当点P在上，点Q在上时，即时，证明，，即可求解；当时，利用可以求解；
（2）根据解析式可画出函数图象，并得到图象的性质；
（3）观察函数图象即可求解．
【详解】（1）解：当时，点P在上，点Q在上，
∴，，
∴，，
∴，，即
又∵，
∴，
∴，
又∵，
∴；
当时，点P，Q在BD上移动，这时；
∴关于的函数表达式为；
（2）函数的图象如图所示，
当，y随x的增大而减小；
（3）结合图像可得当直线在两条虚线之间时，与图象有两个交点，
当过时，，解得：；
当过时，，解得：；
∴结合函数图象，当函数与上述函数的图像有两个交点时的取值范围为．
20．
【分析】本题考查了正方形的性质、勾股定理、相似三角形的判定与性质等知识，熟练掌握相似三角形的判定与性质是解题关键．先求出，再证出，然后根据相似三角形的性质求解即可得．
【详解】解：四边形是正方形，，
，．
，
．
．
于点，
．
，，
．
．
，即，
．
．
21．米
【分析】本题考查了相似三角形的应用，解题的关键是掌握相似三角形的判定与性质．根据题意可求出米，设，则（米），（米），证明，可得，证明，可得到，再列方程求出，即可求解．
【详解】解：由题意知，米，米，米，米，
米，
设，则（米），（米），
，，
，
，
，即，
，
，，
，
，
，即，
，
，
解得：，
米．
22．山峰的高度为70米，它和标杆的水平距离是200米
【分析】本题考查了相似三角形的应用，熟练掌握字模型相似三角形是解题的关键．
根据题意可得：，，，从而可得，然后证明字模型相似，，从而利用相似三角形的性质进行计算，即可解答．
【详解】解：由题意得：，，，
，
，
，
，
，
，
，
，
，
，
解得：，
，
解得：，
山峰的高度为70米，它和标杆的水平距离是200米．
23．(1)
(2)，理由见解析
(3)①；②见解析；③见解析
【分析】（1）根据已知得出是等腰三角形，根据三角形内角和定理即可求解；
（2）方法一：，根据三角形内角和定理得出，同理，，进而得，即可证明；
方法二：延长，交于点，同理证明，即可证明
（3）①根据已知得出，，是等腰直角三角形，根据等腰直角三角形的性质得出，三点共线，可得，进而证明，根据相似三角形的性质即可求解；
②由（2）知，，根据相似三角形的性质即可得证；
②延长，交于点，由①知，则，得出，可得，即可得证．
【详解】（1）∵当时，
∴
又∵是等腰三角形，
∴，
故答案为：．
（2）．
方法一：
理由如下：，
，
同理，，
又，
，
．
方法二：
理由如下：如图，延长，交于点，

，
，
同理，，
，
，
，
．
当点在线段上时，
如图，同理可求，
，
．

（3）①∵，
∴
∴，，是等腰直角三角形，
∵
∴，

∴
∴三点共线，
由（2）知，
，
，
又，
．
又
∴
∴
∴，
解得：（负值舍去）；
②由（2）知，
，
，
又，
．

③如图，延长，交于点，

，
，
又，

由①知，
，
．
即无论为何值，点都在的平分线上．
【点睛】本题考查了相似三角形的性质与判定，等腰三角形的性质与判定，勾股定理，熟练掌握以上知识是解题的关键．
24．见解析
【分析】先根据正方形的性质求出，再根据等量代换求出，最后根据相似三角形的判定和性质证明即可．
【详解】证明：∵ 四边形是正方形，
∴．
又∵，
∴．
又∵，，
∴．
又∵，
∴．
∴．
【点睛】本题考查了正方形的性质和相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)