四川省南充高级中学2024-2025学年高一上学期第二次月考(12月)数学试题(含答案)
文档属性
| 名称 | 四川省南充高级中学2024-2025学年高一上学期第二次月考(12月)数学试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 394.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 11:01:35 | ||
图片预览


文档简介
南充高中高2024级第一学期第二次月考
数 学 试 卷
(考试时间:120分钟 总分:150分 命、审题:)
一、单项选择题:本题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.已知集合,,则( )
A. B. C. D.
2.已知命题,,则命题p的否定为( )
A., B.,
C., D.,
3.函数的定义域是( )
A. B. C. D.
4.已知函数在[2,+∞)上单调递增,则实数a的取值范围是( )
A.{4} B.(-∞,4] C.(-∞,4) D.(-∞,2]
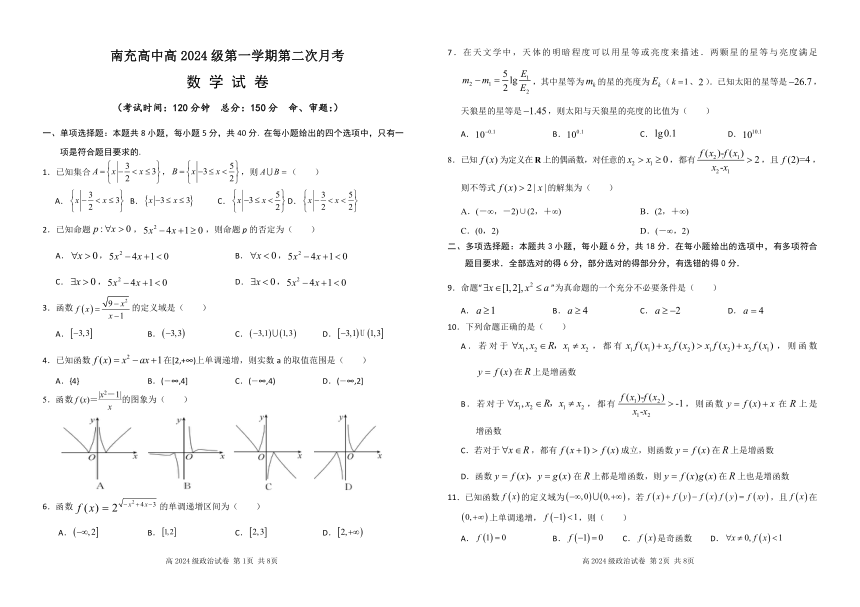
5.函数f (x)=的图象为( )
6.函数的单调递增区间为( )
A. B. C. D.
7.在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足
,其中星等为的星的亮度为(、).已知太阳的星等是,
天狼星的星等是,则太阳与天狼星的亮度的比值为( )
A. B. C. D.
8.已知为定义在R上的偶函数,对任意的,都有,且,
则不等式的解集为( )
A.(-∞,-2)∪(2,+∞) B.(2,+∞)
C.(0,2) D.(-∞,2)
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.命题“”为真命题的一个充分不必要条件是( )
A. B. C. D.
10.下列命题正确的是( )
A.若对于,都有,则函数
在上是增函数
B.若对于,都有,则函数在上是
增函数
C.若对于,都有成立,则函数在上是增函数
D.函数在上都是增函数,则在上也是增函数
11.已知函数的定义域为,若,且在
上单调递增,,则( )
A. B. C.是奇函数 D.
三、填空题:本题共3小题,每小题5分,共15分.
12.函数的图象一定过定点P,则P点的坐标是________.
13.如果函数满足条件:对于定义域内的任意两个,都有
成立,那么称函数为G函数.下列函数:①;
②;③;④.
其中是“G函数”的是 (写出所有符合条件的序号).
14.已知函数的定义域均为R,且.若
的图像关于直线对称,,则 .
四、解答题:本题共5小题,共77分,解答应写出文字说明、证明过程或演算步骤.
15.(13分)
(1)已知,且,求下列各式的值:
①; ②.
(2) .
16.(15分)
已知幂函数为奇函数.
(1)求的解析式;
(2)若正数满足,若不等式恒成立.求的最大值.
17.(15分)
已知函数,且.
(1)求和的值;
(2)判断在上的单调性,并根据定义证明.
18.(17分)
已知、、、为正实数,利用基本不等式证明(1)(2)并指出等号成立条件,然后解(3)中的实际问题.
(1)请根据基本不等式,证明:;
(2)请利用(1)的结论,证明:;
(3)用一段长为的篱笆围成一个一边靠墙的矩形菜园,墙长.当这个矩形的边长为多少时,菜园的面积最大?最大面积是多少?
19.(17分)
已知函数.
(1)解不等式;
(2)若关于x的方程在上有解,求m的取值范围;
(3)若函数,其中为奇函数,为偶函数,若不等式对任意恒成立,求实数a的取值范围.
南充高中高2024级第一学期第二次月考
数 学 答 案
选择题
1~5 BCDBD 6~8 BDA
多选题
BD 10. AB 11. ABD
填空题
(1,4) 13. ②④ 14. -24
解答题
15.①因为,且,所以;……3分
②. ………………………6分
(2)
,故答案为:/. …………………………13分
16.(1)为幂函数,,解得:或;……3分
当时,,则,即为偶函数,不合题意,舍去;
当时,,则,即为奇函数,符合题意;
综上所述:. …………………7分
由(1)得:,即,又,,
……………13分
当且仅当,即,时取等号.
. …………………………15分
17.(1)因为,所以,解得. ……5分
(2)由(1)知:,在上的单调递减.………………………8分
证明如下:
在上任取,且,
,
∵,
∴,,,
∴,∴,在上的单调递减. ………………15分
18.(1)证明:因为,,当且仅当,时等号成立,
所以当且仅当,时等号成立.
所以,当且仅当时等号成立,
所以,当且仅当时等号成立.…………5分
(2)解:由于,当且仅当时等号成立,
令, 得,
即,故.
所以,当且仅当时等号成立. ………………10分
(3)设矩形菜园平行于墙的一边的长为,与之相邻的边的长为,菜园的面积为,
则,.其中,即. ………………12分
由基本不等式得.…………15分
当,即,时,菜园的面积最大,最大面积是.
因此,当矩形菜园平行于墙的一边的长为15m,与之相邻的边的长为m时,
菜园的面积最大,最大面积是 …………………………………17分
19.(1)设,则不等式可化为,解得,
则,故原不等式的解集为 ………………………………………3分
(2)即在上有解,
而,,故,即m的取值范围是…………7分
(3)由题意得,,
解得,,………………………………………10分
故原不等式即对恒成立,
令,不等式可化为对恒成立,
, ………………………………………14分
而,由对勾函数性质得当时取最大值,
则,实数a的取值范围是 ………………………………………17分
高2024级政治试卷 第1页 共8页 高2024级政治试卷 第2页 共8页
数 学 试 卷
(考试时间:120分钟 总分:150分 命、审题:)
一、单项选择题:本题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一
项是符合题目要求的.
1.已知集合,,则( )
A. B. C. D.
2.已知命题,,则命题p的否定为( )
A., B.,
C., D.,
3.函数的定义域是( )
A. B. C. D.
4.已知函数在[2,+∞)上单调递增,则实数a的取值范围是( )
A.{4} B.(-∞,4] C.(-∞,4) D.(-∞,2]
5.函数f (x)=的图象为( )
6.函数的单调递增区间为( )
A. B. C. D.
7.在天文学中,天体的明暗程度可以用星等或亮度来描述.两颗星的星等与亮度满足
,其中星等为的星的亮度为(、).已知太阳的星等是,
天狼星的星等是,则太阳与天狼星的亮度的比值为( )
A. B. C. D.
8.已知为定义在R上的偶函数,对任意的,都有,且,
则不等式的解集为( )
A.(-∞,-2)∪(2,+∞) B.(2,+∞)
C.(0,2) D.(-∞,2)
二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合
题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.命题“”为真命题的一个充分不必要条件是( )
A. B. C. D.
10.下列命题正确的是( )
A.若对于,都有,则函数
在上是增函数
B.若对于,都有,则函数在上是
增函数
C.若对于,都有成立,则函数在上是增函数
D.函数在上都是增函数,则在上也是增函数
11.已知函数的定义域为,若,且在
上单调递增,,则( )
A. B. C.是奇函数 D.
三、填空题:本题共3小题,每小题5分,共15分.
12.函数的图象一定过定点P,则P点的坐标是________.
13.如果函数满足条件:对于定义域内的任意两个,都有
成立,那么称函数为G函数.下列函数:①;
②;③;④.
其中是“G函数”的是 (写出所有符合条件的序号).
14.已知函数的定义域均为R,且.若
的图像关于直线对称,,则 .
四、解答题:本题共5小题,共77分,解答应写出文字说明、证明过程或演算步骤.
15.(13分)
(1)已知,且,求下列各式的值:
①; ②.
(2) .
16.(15分)
已知幂函数为奇函数.
(1)求的解析式;
(2)若正数满足,若不等式恒成立.求的最大值.
17.(15分)
已知函数,且.
(1)求和的值;
(2)判断在上的单调性,并根据定义证明.
18.(17分)
已知、、、为正实数,利用基本不等式证明(1)(2)并指出等号成立条件,然后解(3)中的实际问题.
(1)请根据基本不等式,证明:;
(2)请利用(1)的结论,证明:;
(3)用一段长为的篱笆围成一个一边靠墙的矩形菜园,墙长.当这个矩形的边长为多少时,菜园的面积最大?最大面积是多少?
19.(17分)
已知函数.
(1)解不等式;
(2)若关于x的方程在上有解,求m的取值范围;
(3)若函数,其中为奇函数,为偶函数,若不等式对任意恒成立,求实数a的取值范围.
南充高中高2024级第一学期第二次月考
数 学 答 案
选择题
1~5 BCDBD 6~8 BDA
多选题
BD 10. AB 11. ABD
填空题
(1,4) 13. ②④ 14. -24
解答题
15.①因为,且,所以;……3分
②. ………………………6分
(2)
,故答案为:/. …………………………13分
16.(1)为幂函数,,解得:或;……3分
当时,,则,即为偶函数,不合题意,舍去;
当时,,则,即为奇函数,符合题意;
综上所述:. …………………7分
由(1)得:,即,又,,
……………13分
当且仅当,即,时取等号.
. …………………………15分
17.(1)因为,所以,解得. ……5分
(2)由(1)知:,在上的单调递减.………………………8分
证明如下:
在上任取,且,
,
∵,
∴,,,
∴,∴,在上的单调递减. ………………15分
18.(1)证明:因为,,当且仅当,时等号成立,
所以当且仅当,时等号成立.
所以,当且仅当时等号成立,
所以,当且仅当时等号成立.…………5分
(2)解:由于,当且仅当时等号成立,
令, 得,
即,故.
所以,当且仅当时等号成立. ………………10分
(3)设矩形菜园平行于墙的一边的长为,与之相邻的边的长为,菜园的面积为,
则,.其中,即. ………………12分
由基本不等式得.…………15分
当,即,时,菜园的面积最大,最大面积是.
因此,当矩形菜园平行于墙的一边的长为15m,与之相邻的边的长为m时,
菜园的面积最大,最大面积是 …………………………………17分
19.(1)设,则不等式可化为,解得,
则,故原不等式的解集为 ………………………………………3分
(2)即在上有解,
而,,故,即m的取值范围是…………7分
(3)由题意得,,
解得,,………………………………………10分
故原不等式即对恒成立,
令,不等式可化为对恒成立,
, ………………………………………14分
而,由对勾函数性质得当时取最大值,
则,实数a的取值范围是 ………………………………………17分
高2024级政治试卷 第1页 共8页 高2024级政治试卷 第2页 共8页
同课章节目录
