浙江省温州市龙湾区、瑞安联考2024-2025学年九年级上学期期末数学试题(含答案)
文档属性
| 名称 | 浙江省温州市龙湾区、瑞安联考2024-2025学年九年级上学期期末数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 645.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-13 11:50:11 | ||
图片预览


文档简介
2024学年第一学期九年级第15周监测数学卷 2024.12
卷首语:
1.本卷共4页,考试时间120分钟,满分120分;
2.全卷由试题卷和答题卡两部分组成,请将答案写在答题卡相应的位置;
3.书写时字迹要工整,清晰,请勿使用涂改液、修正带等,不得使用计算器.
希望你沉着冷静,让智慧在笔尖流淌,用细心为成功奠基!
选择题(共10小题,每题3分)
1.如图是一个游戏转盘.自由转动转盘,当转盘停止转动后,指针最大可能落在( ▲ )
A.紫色区域 B.红色区域 C.黄色区域 D.蓝色区域
2.若函数,则函数值y有( ▲ )
A.最大值 B.最小值 C.最大值3 D.最小值3
3.如图,AB∥CD,AD,BC交于点E,若EC=2BE,△ABE的周长为3,则△CDE的周长为( ▲ )
A.4 B.6 C.9 D.12
4.圆心角为120°,半径为3的扇形弧长为( ▲ )
A. B. C. D.
5.如图,在平面直角坐标系中,△ABC和△DEF是位似三角形,且CO=2FO,若点E(2,-1),则点B的坐标为 ( ▲ )
A.(4,-2) B.(4,2) C.(-4,2) D.(-4,-2)
6.某校即将举行田径运动会,“体育达人”小明从“跳高”“跳远”“100米”“800米”四个项目中,随机选择两项,则他选择“跳远”与“800米”两个项目的概率是(▲ )
A. B. C. D.
7.如图,AB为⊙O直径,弦CD与AB相交,连结AC,BC,AD,若∠CAB=42°,则∠D的度数为( ▲ )
A.42° B.48° C.52° D.58°
8.抛物线 经过点(1,m),则m的值为( ▲ )
A. B. C. D.2
9.如图,五边形ABCDE内接于半径为6的⊙O,F为CD中点,连结OF,若AB=AE,BC=CD=DE,=90°,则OF的长为( ▲ )
A. B.5 C.4 D.
10.已知抛物线y=ax2+bx+b-a(a<0),当-1≤x≤4时,最大值与最小值的差为,若将抛物线向左平移 4个单位后经过点(-1,0),则a的值为( ▲ )
A. B. C. D.
二、填空题(共6小题,每题3分)
11.已知⊙O的半径为6cm,点A在⊙O外,则OA的长可以为 ▲ .
12.如图,正六边形ABCDEF是由6个大小相等的等边三角形构成,随机地往六边形ABCDEF内投一粒米,落在阴影区域的概率为 ▲ .
13.若抛物线上的顶点坐标为(3,4)则m+k的值为 ▲ .
14.把一个矩形ABCD按如图方式划分成三个全等的小矩形,每一个小矩形与原矩形相似,若BC=9,则AB的长为 ▲ .
15.如图,在△ABC中,∠C=60°,AC=8,BC=6,点D在边AC上运动,DE⊥BC于点E,则△BDE的面积的最大值为 ▲ .
如图,在△ABC中,DE∥BC,分别交边AB,AC于点D,E,连结DC,
BE交于点F,若△DEF的面积为3,△ADE的面积为13,
则的值为 ▲ ;△FBC的面积为 ▲ .
三、解答题(17-21每题8分,22、23每题10分,24题12分)
17.已知实数a,b满足.
(1)求的值. (2)若,求m的值.
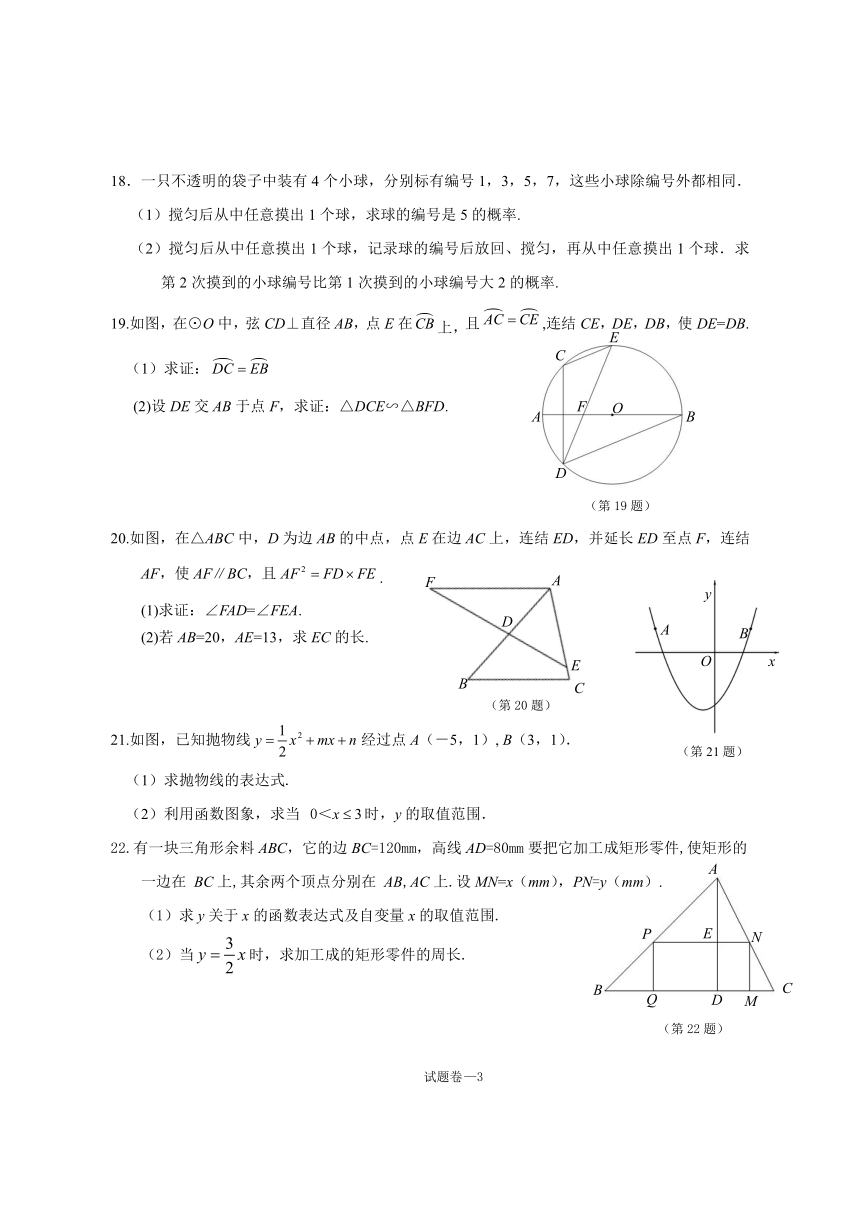
18.一只不透明的袋子中装有4个小球,分别标有编号1,3,5,7,这些小球除编号外都相同.
(1)搅匀后从中任意摸出1个球,求球的编号是5的概率.
(2)搅匀后从中任意摸出1个球,记录球的编号后放回、搅匀,再从中任意摸出1个球.求第2次摸到的小球编号比第1次摸到的小球编号大2的概率.
19.如图,在⊙O中,弦CD⊥直径AB,点E在上,且,连结CE,DE,DB,使DE=DB.
(1)求证:
(2)设DE交AB于点F,求证:△DCE∽△BFD.
20.如图,在△ABC中,D为边AB的中点,点E在边AC上,连结ED,并延长ED至点F,连结AF,使AF∥BC,且.
(1)求证:∠FAD=∠FEA.
(2)若AB=20,AE=13,求EC的长.
21.如图,已知抛物线经过点A(-5,1), B(3,1).
(1)求抛物线的表达式.
(2)利用函数图象,求当 时,y的取值范围.
22.有一块三角形余料ABC,它的边BC=120mm,高线AD=80mm要把它加工成矩形零件,使矩形的一边在 BC上,其余两个顶点分别在 AB,AC上.设MN=x(mm),PN=y(mm).
求y关于x的函数表达式及自变量x的取值范围.
当时,求加工成的矩形零件的周长.
23.尺规作图题:
如图1,在上⊙O依次取点A,B,C,使,点D在上,连结AC,AD,用尺规
作弦AE,连结EC,DA,BE的延长线交于点F,使△AEF≌△AEC.
小明:如图2,连结CD,作△DAC的外角平分线AE交⊙O于另一点E,连结EC,作DA,BE的延长线交于点F,则△AEF≌△AEC.
小通:作弦AB的垂直平分线EH,交于点E,连结AE,EC,作DA,BE的延长线交于点F,则△AEF≌△AEC.
小明:小通,你的作法有问题.
小通:哦------我明白了.
(1)求证:△AEF≌△AEC.
(2)指出小通作法中存在的问题.
24.如图,在圆内接△ABC中,∠ABC>90°,弦BD>AC,延长AD至点E,延长BA至点F,连结EF,使EF=BD,延长CD交EF于点G,使∠EGD+∠DAB=180°,延长CB,DA交于点H.
(1)若∠EGD=75°,CD为直径,求∠BAC的度数.
(2)求证:.
(3)求证:AE=AC.
2024学年第一学期九年级第15周监测数学卷
参考答案和评分标准
一、选择题(本题有10小题,每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B B C A C B D A B
二、填空题(本题有6小题,每小题3分,共18分)
11.不唯一,满足OA>6 12. 13.1
14. 15. 16.;
三、解答题(17-21每题8分,22、23每题10分,24题12分)
17.(本题8分)
解:(1)∵,∴. (4分)
∵,,∴,去分母,得,
解得,经检验,m=6符合题意,∴m=6. (4分)
18.(本题8分)
(1) (4分) (2) (4分)
19.(本题8分)
证明:(1)∵弦CD⊥直径AB,∴.∵DE=DB,∴,∴.
即.∴. (4分)
(2)∵,∴∠E=∠BDF.∵弦CD⊥直径AB,∴.∵,
∴.∴∠B=∠CDE.又∵∠E=∠BDF,∴△DCE∽△BFD. (4分)
(本题8分)
(1)证明:∵,∴.∵∠F=∠F,
∴△AFD∽△EFA.∴∠FAD=∠FEA. (4分)
∵AF∥BC,∴∠FAD=∠B.∵∠FAD=∠FEA ,∴∠B=∠FEA.
又∵∠DAE=∠CAB ,∴△ADE∽△ACB,∴.
∵D为边AB的中点,AB=20,∴AD=10.∵AE=13,
∴.解得. (4分)
(本题8分)
解:(1),
∴. (4分)
(2)把x=0代入.
由图象,得当时,. (4分)
(本题10分)
解:(1)∵PN∥BC,AD⊥BC,∴AD⊥PN.
∵PN∥BC,∴△APN∽△ABC,∴.即.
化简,得(). (5分)
把代入,得,解得,,
经检验,x,y的取值均符合题意,
∴加工成的矩形零件的周长=2(x+y)=200 mm. (5分)
23.(本题10分)
(1)证明:如图2,连结BC,∵四边形AEBC内接于⊙O,∴∠AEF=∠ACB.
∵ ,∴∠AEC=∠ACB,得∠AEF=∠AEC.又∵AE=AE,∠EAF=∠EAC,
∴△AEF≌△AEC. (6分)
(2)小通的作法由于不能确保条件∠EAF=∠EAC,导致无法证明△AEF≌△AEC. (2分)
理由如下(如图3):
连结DC,∵四边形AECD内接于⊙O,∴∠EAF=∠ECD.
∠ECD,∠EAC所对弧分别是,而已知条件只提供,
因此无法确保条件∠ECD=∠EAC成立,
进而无法确保条件∠EAF=∠EAC成立,
因此导致无法证明△AEF≌△AEC. (2分)
24.(本题12分)
(1)解:连结CD,
∵四边形ABCD内接于圆,∴∠DCB+∠DAB=180°.∵∠EGD+∠DAB=180°,
∴∠DCB=∠EGD=75°.∵CD为直径,∴∠DBC=90°.∴∠BAC=∠BDC=15°. (4分)
(2)∵四边形ABCD内接于圆,∴∠DCB+∠DAB=180°,∵∠EGD+∠DAB=180°,
∴∠DCB=∠EGD.∴EF∥BH.∴. (4分)
(3)∵,∴.易得△HAC∽△HBD,得,∴.
又∵EF=BD,∴AE=AC. (4分)
(第23题)
C
A
B
E
D
F
O
x
y
(第5题)
(第7题)
C
A
B
O
D
(第1题)
红色
黄色
蓝色
紫色
(第3题)
A
B
C
D
E
(第12题)
C
A
B
E
D
F
C
A
B
E
D
(第15题)
(第9题)
A
B
C
O
D
E
F
C
A
B
D
(第14题)
(第16题)
C
A
B
E
D
F
(第19题)
A
C
B
D
O
E
F
A
C
B
D
F
E
(第20题)
(第21题)
x
O
B
A
y
(第22题)
A
C
B
D
P
E
Q
M
N
F
A
C
B
D
O
E
图2
F
A
C
B
D
O
E
图2
A
C
B
D
O
图1
(第23题)
(第24题)
A
C
B
D
E
G
F
H
(第19题)
A
C
B
D
O
E
F
A
C
B
D
F
E
(第20题)
(第22题)
A
C
B
D
P
E
Q
M
N
E
F
A
C
B
D
O
图2
F
A
C
B
D
O
E
图3
(第24题)
A
C
B
D
E
G
F
H
PAGE
试题卷
卷首语:
1.本卷共4页,考试时间120分钟,满分120分;
2.全卷由试题卷和答题卡两部分组成,请将答案写在答题卡相应的位置;
3.书写时字迹要工整,清晰,请勿使用涂改液、修正带等,不得使用计算器.
希望你沉着冷静,让智慧在笔尖流淌,用细心为成功奠基!
选择题(共10小题,每题3分)
1.如图是一个游戏转盘.自由转动转盘,当转盘停止转动后,指针最大可能落在( ▲ )
A.紫色区域 B.红色区域 C.黄色区域 D.蓝色区域
2.若函数,则函数值y有( ▲ )
A.最大值 B.最小值 C.最大值3 D.最小值3
3.如图,AB∥CD,AD,BC交于点E,若EC=2BE,△ABE的周长为3,则△CDE的周长为( ▲ )
A.4 B.6 C.9 D.12
4.圆心角为120°,半径为3的扇形弧长为( ▲ )
A. B. C. D.
5.如图,在平面直角坐标系中,△ABC和△DEF是位似三角形,且CO=2FO,若点E(2,-1),则点B的坐标为 ( ▲ )
A.(4,-2) B.(4,2) C.(-4,2) D.(-4,-2)
6.某校即将举行田径运动会,“体育达人”小明从“跳高”“跳远”“100米”“800米”四个项目中,随机选择两项,则他选择“跳远”与“800米”两个项目的概率是(▲ )
A. B. C. D.
7.如图,AB为⊙O直径,弦CD与AB相交,连结AC,BC,AD,若∠CAB=42°,则∠D的度数为( ▲ )
A.42° B.48° C.52° D.58°
8.抛物线 经过点(1,m),则m的值为( ▲ )
A. B. C. D.2
9.如图,五边形ABCDE内接于半径为6的⊙O,F为CD中点,连结OF,若AB=AE,BC=CD=DE,=90°,则OF的长为( ▲ )
A. B.5 C.4 D.
10.已知抛物线y=ax2+bx+b-a(a<0),当-1≤x≤4时,最大值与最小值的差为,若将抛物线向左平移 4个单位后经过点(-1,0),则a的值为( ▲ )
A. B. C. D.
二、填空题(共6小题,每题3分)
11.已知⊙O的半径为6cm,点A在⊙O外,则OA的长可以为 ▲ .
12.如图,正六边形ABCDEF是由6个大小相等的等边三角形构成,随机地往六边形ABCDEF内投一粒米,落在阴影区域的概率为 ▲ .
13.若抛物线上的顶点坐标为(3,4)则m+k的值为 ▲ .
14.把一个矩形ABCD按如图方式划分成三个全等的小矩形,每一个小矩形与原矩形相似,若BC=9,则AB的长为 ▲ .
15.如图,在△ABC中,∠C=60°,AC=8,BC=6,点D在边AC上运动,DE⊥BC于点E,则△BDE的面积的最大值为 ▲ .
如图,在△ABC中,DE∥BC,分别交边AB,AC于点D,E,连结DC,
BE交于点F,若△DEF的面积为3,△ADE的面积为13,
则的值为 ▲ ;△FBC的面积为 ▲ .
三、解答题(17-21每题8分,22、23每题10分,24题12分)
17.已知实数a,b满足.
(1)求的值. (2)若,求m的值.
18.一只不透明的袋子中装有4个小球,分别标有编号1,3,5,7,这些小球除编号外都相同.
(1)搅匀后从中任意摸出1个球,求球的编号是5的概率.
(2)搅匀后从中任意摸出1个球,记录球的编号后放回、搅匀,再从中任意摸出1个球.求第2次摸到的小球编号比第1次摸到的小球编号大2的概率.
19.如图,在⊙O中,弦CD⊥直径AB,点E在上,且,连结CE,DE,DB,使DE=DB.
(1)求证:
(2)设DE交AB于点F,求证:△DCE∽△BFD.
20.如图,在△ABC中,D为边AB的中点,点E在边AC上,连结ED,并延长ED至点F,连结AF,使AF∥BC,且.
(1)求证:∠FAD=∠FEA.
(2)若AB=20,AE=13,求EC的长.
21.如图,已知抛物线经过点A(-5,1), B(3,1).
(1)求抛物线的表达式.
(2)利用函数图象,求当 时,y的取值范围.
22.有一块三角形余料ABC,它的边BC=120mm,高线AD=80mm要把它加工成矩形零件,使矩形的一边在 BC上,其余两个顶点分别在 AB,AC上.设MN=x(mm),PN=y(mm).
求y关于x的函数表达式及自变量x的取值范围.
当时,求加工成的矩形零件的周长.
23.尺规作图题:
如图1,在上⊙O依次取点A,B,C,使,点D在上,连结AC,AD,用尺规
作弦AE,连结EC,DA,BE的延长线交于点F,使△AEF≌△AEC.
小明:如图2,连结CD,作△DAC的外角平分线AE交⊙O于另一点E,连结EC,作DA,BE的延长线交于点F,则△AEF≌△AEC.
小通:作弦AB的垂直平分线EH,交于点E,连结AE,EC,作DA,BE的延长线交于点F,则△AEF≌△AEC.
小明:小通,你的作法有问题.
小通:哦------我明白了.
(1)求证:△AEF≌△AEC.
(2)指出小通作法中存在的问题.
24.如图,在圆内接△ABC中,∠ABC>90°,弦BD>AC,延长AD至点E,延长BA至点F,连结EF,使EF=BD,延长CD交EF于点G,使∠EGD+∠DAB=180°,延长CB,DA交于点H.
(1)若∠EGD=75°,CD为直径,求∠BAC的度数.
(2)求证:.
(3)求证:AE=AC.
2024学年第一学期九年级第15周监测数学卷
参考答案和评分标准
一、选择题(本题有10小题,每小题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 A B B C A C B D A B
二、填空题(本题有6小题,每小题3分,共18分)
11.不唯一,满足OA>6 12. 13.1
14. 15. 16.;
三、解答题(17-21每题8分,22、23每题10分,24题12分)
17.(本题8分)
解:(1)∵,∴. (4分)
∵,,∴,去分母,得,
解得,经检验,m=6符合题意,∴m=6. (4分)
18.(本题8分)
(1) (4分) (2) (4分)
19.(本题8分)
证明:(1)∵弦CD⊥直径AB,∴.∵DE=DB,∴,∴.
即.∴. (4分)
(2)∵,∴∠E=∠BDF.∵弦CD⊥直径AB,∴.∵,
∴.∴∠B=∠CDE.又∵∠E=∠BDF,∴△DCE∽△BFD. (4分)
(本题8分)
(1)证明:∵,∴.∵∠F=∠F,
∴△AFD∽△EFA.∴∠FAD=∠FEA. (4分)
∵AF∥BC,∴∠FAD=∠B.∵∠FAD=∠FEA ,∴∠B=∠FEA.
又∵∠DAE=∠CAB ,∴△ADE∽△ACB,∴.
∵D为边AB的中点,AB=20,∴AD=10.∵AE=13,
∴.解得. (4分)
(本题8分)
解:(1),
∴. (4分)
(2)把x=0代入.
由图象,得当时,. (4分)
(本题10分)
解:(1)∵PN∥BC,AD⊥BC,∴AD⊥PN.
∵PN∥BC,∴△APN∽△ABC,∴.即.
化简,得(). (5分)
把代入,得,解得,,
经检验,x,y的取值均符合题意,
∴加工成的矩形零件的周长=2(x+y)=200 mm. (5分)
23.(本题10分)
(1)证明:如图2,连结BC,∵四边形AEBC内接于⊙O,∴∠AEF=∠ACB.
∵ ,∴∠AEC=∠ACB,得∠AEF=∠AEC.又∵AE=AE,∠EAF=∠EAC,
∴△AEF≌△AEC. (6分)
(2)小通的作法由于不能确保条件∠EAF=∠EAC,导致无法证明△AEF≌△AEC. (2分)
理由如下(如图3):
连结DC,∵四边形AECD内接于⊙O,∴∠EAF=∠ECD.
∠ECD,∠EAC所对弧分别是,而已知条件只提供,
因此无法确保条件∠ECD=∠EAC成立,
进而无法确保条件∠EAF=∠EAC成立,
因此导致无法证明△AEF≌△AEC. (2分)
24.(本题12分)
(1)解:连结CD,
∵四边形ABCD内接于圆,∴∠DCB+∠DAB=180°.∵∠EGD+∠DAB=180°,
∴∠DCB=∠EGD=75°.∵CD为直径,∴∠DBC=90°.∴∠BAC=∠BDC=15°. (4分)
(2)∵四边形ABCD内接于圆,∴∠DCB+∠DAB=180°,∵∠EGD+∠DAB=180°,
∴∠DCB=∠EGD.∴EF∥BH.∴. (4分)
(3)∵,∴.易得△HAC∽△HBD,得,∴.
又∵EF=BD,∴AE=AC. (4分)
(第23题)
C
A
B
E
D
F
O
x
y
(第5题)
(第7题)
C
A
B
O
D
(第1题)
红色
黄色
蓝色
紫色
(第3题)
A
B
C
D
E
(第12题)
C
A
B
E
D
F
C
A
B
E
D
(第15题)
(第9题)
A
B
C
O
D
E
F
C
A
B
D
(第14题)
(第16题)
C
A
B
E
D
F
(第19题)
A
C
B
D
O
E
F
A
C
B
D
F
E
(第20题)
(第21题)
x
O
B
A
y
(第22题)
A
C
B
D
P
E
Q
M
N
F
A
C
B
D
O
E
图2
F
A
C
B
D
O
E
图2
A
C
B
D
O
图1
(第23题)
(第24题)
A
C
B
D
E
G
F
H
(第19题)
A
C
B
D
O
E
F
A
C
B
D
F
E
(第20题)
(第22题)
A
C
B
D
P
E
Q
M
N
E
F
A
C
B
D
O
图2
F
A
C
B
D
O
E
图3
(第24题)
A
C
B
D
E
G
F
H
PAGE
试题卷
同课章节目录
