2025苏教版高中数学选择性必修第二册强化练习题(含解析)--专题强化练2 利用向量法求空间角和空间距离
文档属性
| 名称 | 2025苏教版高中数学选择性必修第二册强化练习题(含解析)--专题强化练2 利用向量法求空间角和空间距离 |
|
|
| 格式 | docx | ||
| 文件大小 | 404.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-12-15 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025苏教版高中数学选择性必修第二册
专题强化练2 利用向量法求空间角和空间距离
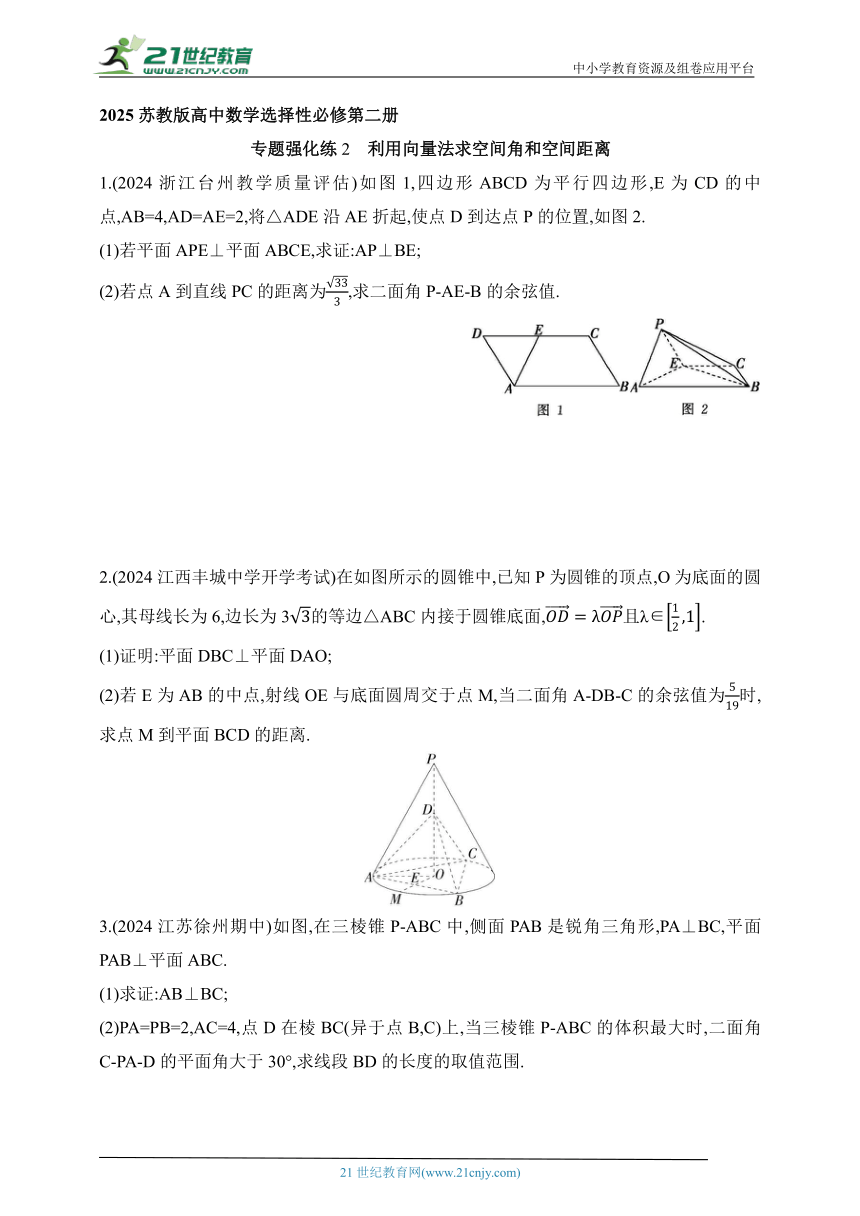
1.(2024浙江台州教学质量评估)如图1,四边形ABCD为平行四边形,E为CD的中点,AB=4,AD=AE=2,将△ADE沿AE折起,使点D到达点P的位置,如图2.
(1)若平面APE⊥平面ABCE,求证:AP⊥BE;
(2)若点A到直线PC的距离为,求二面角P-AE-B的余弦值.
2.(2024江西丰城中学开学考试)在如图所示的圆锥中,已知P为圆锥的顶点,O为底面的圆心,其母线长为6,边长为3的等边△ABC内接于圆锥底面,且λ∈.
(1)证明:平面DBC⊥平面DAO;
(2)若E为AB的中点,射线OE与底面圆周交于点M,当二面角A-DB-C的余弦值为时,求点M到平面BCD的距离.
3.(2024江苏徐州期中)如图,在三棱锥P-ABC中,侧面PAB是锐角三角形,PA⊥BC,平面PAB⊥平面ABC.
(1)求证:AB⊥BC;
(2)PA=PB=2,AC=4,点D在棱BC(异于点B,C)上,当三棱锥P-ABC的体积最大时,二面角C-PA-D的平面角大于30°,求线段BD的长度的取值范围.
4.(2024江苏无锡太湖高级中学阶段性考试)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥平面ABCD,M,N分别为BC,PA的中点,且AB=AC=1,AD=.
(1)若PA=1,求直线MN与平面PBC所成角的正弦值;
(2)若直线AC与平面PBC所成角的正弦值的取值范围为,求平面PBC与平面ABCD所成锐二面角的余弦值的取值范围.
答案与分层梯度式解析
专题强化练2 利用向量法求空间角和空间距离
1.解析 (1)证明:由题易知△ADE为等边三角形,又四边形ABCD为平行四边形,所以∠AEC=∠BCE=120°.
因为E为CD的中点,所以CE=CB,所以△BCE为等腰三角形,所以∠CEB=30°,所以∠AEB=90°,即BE⊥AE.
又平面APE⊥平面ABCE,平面APE∩平面ABCE=AE,BE 平面ABCE,所以BE⊥平面APE.
又AP 平面APE,所以AP⊥BE.
(2)取AE的中点O,连接PO.
因为△APE为等边三角形,所以PO⊥AE.
取AB的中点G,连接OG,则OG∥BE.
由(1)得BE⊥AE,所以OG⊥AE.
以O为坐标原点,OA,OG所在直线分别为x轴,y轴建立如图所示的空间直角坐标系,
则A(1,0,0),C(-2,,0).
设二面角P-AE-B的平面角为θ,即∠POG=θ.
易知OP=,则P(0,cos θ,sin θ),
所以cos θ,-sin θ),
cos θ,-sin θ),
所以点A到直线PC的距离为,解得cos θ=-或cos θ=,所以二面角P-AE-B的余弦值为-.
2.解析 (1)证明:由题意可得OP⊥平面ABC,又BC 平面ABC,∴OP⊥BC,即OD⊥BC.
∵O为△ABC外接圆的圆心,且△ABC为正三角形,∴OA⊥BC.
又OA∩OD=O,OA,OD 平面DAO,
∴BC⊥平面DAO,
又BC 平面DBC,∴平面DBC⊥平面DAO.
(2)延长AO交BC于点F,则F为BC的中点,作OG∥BC交AB于G,
∵OA⊥BC,OG∥BC,∴OA⊥OG,即OF⊥OG.
∵OD⊥平面ABC,OG,OF 平面ABC,
∴OD⊥OG,OD⊥OF.
以O为坐标原点,OG,OF,OD所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图,
则O(0,0,0),A(0,-3,0),B),
所以,0,0),
由,得D(0,0,3λ),
则λ).
设平面ABD的一个法向量为m=(x1,y1,z1),
则
令y1=λ,得x1=-3λ,z1=-1,则m=(-3λ,λ,-1).
设平面BCD的一个法向量为n=(x2,y2,z2),
则
令y2=6λ,得x2=0,z2=3,则n=(0,6λ,3).
所以|cos|=,且λ∈,
所以λ=,
所以D(0,0,2),n=(0,4,3),
易知M,
所以,
所以点M到平面BCD的距离d=.
3.解析 (1)证明:过点P作PE⊥AB于点E,
因为平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PE 平面PAB,
所以PE⊥平面ABC,
又因为BC 平面ABC,所以PE⊥BC,
又PA⊥BC,PE∩PA=P,PE,PA 平面PAB,
所以BC⊥平面PAB,
又AB 平面PAB,所以AB⊥BC.
(2)设AB=2a,BC=2b,由AB⊥BC,得AB2+BC2=AC2,即4a2+4b2=16,所以a2+b2=4,所以b=,
易知PE=,
所以VP-ABC=a(4-a2),
令f(a)=a(4-a2),则f '(a)=(4-3a2),
令f '(a)=0,解得a=,
当00,f(a)单调递增;
当所以当a=,即AB=时,三棱锥P-ABC的体积最大.
以B为原点,BC,BA所在直线分别为x轴,y轴,过点B且垂直于平面ABC的直线为z轴,建立空间直角坐标系,如图所示,
设BD=m,m>0,则D(m,0,0),C,
所以,
设平面CPA的一个法向量为n1=(x1,y1,z1),
则
令y1=,得x1=1,z1=1,则n1=(1,,1),
设平面PAD的一个法向量为n2=(x2,y2,z2),
则
令y2=,得x2=,z2=1,则n2=,
设二面角C-PA-D的平面角为θ,
则cos θ=解得0所以线段BD的长度的取值范围为.
4.解析 因为四边形ABCD为平行四边形,AB=AC=1,AD=,所以AB2+AC2=AD2=BC2,所以AB⊥AC,
因为PA⊥平面ABCD,AB,AC 平面ABCD,所以PA⊥AB,PA⊥AC,
以A为坐标原点,建立如图所示的空间直角坐标系A-xyz.
(1)易得P(0,0,1),B(1,0,0),C(0,1,0),M,
所以,
设平面PBC的一个法向量为n=(x1,y1,z1),
则
令x1=1,得y1=1,z1=1,则n=(1,1,1),
设直线MN与平面PBC所成的角为θ,
则sin θ=|cos<,n>|=,
所以直线MN与平面PBC所成角的正弦值为.
(2)设PA=h(h>0),则A(0,0,0),P(0,0,h),B(1,0,0),C(0,1,0),所以=(0,1,0),
设平面PBC的一个法向量为m=(x2,y2,z2),
则
令x2=h,得y2=h,z2=1,则m=(h,h,1),
易得平面ABCD的一个法向量n0=(0,0,1),
设直线AC与平面PBC所成的角为α,
则sin α=|cos<,m>|=,
即0<,解得0设平面PBC与平面ABCD所成锐二面角的平面角为β,则cos β=|cos|=,
因为0所以平面PBC与平面ABCD所成锐二面角的余弦值的取值范围为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025苏教版高中数学选择性必修第二册
专题强化练2 利用向量法求空间角和空间距离
1.(2024浙江台州教学质量评估)如图1,四边形ABCD为平行四边形,E为CD的中点,AB=4,AD=AE=2,将△ADE沿AE折起,使点D到达点P的位置,如图2.
(1)若平面APE⊥平面ABCE,求证:AP⊥BE;
(2)若点A到直线PC的距离为,求二面角P-AE-B的余弦值.
2.(2024江西丰城中学开学考试)在如图所示的圆锥中,已知P为圆锥的顶点,O为底面的圆心,其母线长为6,边长为3的等边△ABC内接于圆锥底面,且λ∈.
(1)证明:平面DBC⊥平面DAO;
(2)若E为AB的中点,射线OE与底面圆周交于点M,当二面角A-DB-C的余弦值为时,求点M到平面BCD的距离.
3.(2024江苏徐州期中)如图,在三棱锥P-ABC中,侧面PAB是锐角三角形,PA⊥BC,平面PAB⊥平面ABC.
(1)求证:AB⊥BC;
(2)PA=PB=2,AC=4,点D在棱BC(异于点B,C)上,当三棱锥P-ABC的体积最大时,二面角C-PA-D的平面角大于30°,求线段BD的长度的取值范围.
4.(2024江苏无锡太湖高级中学阶段性考试)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥平面ABCD,M,N分别为BC,PA的中点,且AB=AC=1,AD=.
(1)若PA=1,求直线MN与平面PBC所成角的正弦值;
(2)若直线AC与平面PBC所成角的正弦值的取值范围为,求平面PBC与平面ABCD所成锐二面角的余弦值的取值范围.
答案与分层梯度式解析
专题强化练2 利用向量法求空间角和空间距离
1.解析 (1)证明:由题易知△ADE为等边三角形,又四边形ABCD为平行四边形,所以∠AEC=∠BCE=120°.
因为E为CD的中点,所以CE=CB,所以△BCE为等腰三角形,所以∠CEB=30°,所以∠AEB=90°,即BE⊥AE.
又平面APE⊥平面ABCE,平面APE∩平面ABCE=AE,BE 平面ABCE,所以BE⊥平面APE.
又AP 平面APE,所以AP⊥BE.
(2)取AE的中点O,连接PO.
因为△APE为等边三角形,所以PO⊥AE.
取AB的中点G,连接OG,则OG∥BE.
由(1)得BE⊥AE,所以OG⊥AE.
以O为坐标原点,OA,OG所在直线分别为x轴,y轴建立如图所示的空间直角坐标系,
则A(1,0,0),C(-2,,0).
设二面角P-AE-B的平面角为θ,即∠POG=θ.
易知OP=,则P(0,cos θ,sin θ),
所以cos θ,-sin θ),
cos θ,-sin θ),
所以点A到直线PC的距离为,解得cos θ=-或cos θ=,所以二面角P-AE-B的余弦值为-.
2.解析 (1)证明:由题意可得OP⊥平面ABC,又BC 平面ABC,∴OP⊥BC,即OD⊥BC.
∵O为△ABC外接圆的圆心,且△ABC为正三角形,∴OA⊥BC.
又OA∩OD=O,OA,OD 平面DAO,
∴BC⊥平面DAO,
又BC 平面DBC,∴平面DBC⊥平面DAO.
(2)延长AO交BC于点F,则F为BC的中点,作OG∥BC交AB于G,
∵OA⊥BC,OG∥BC,∴OA⊥OG,即OF⊥OG.
∵OD⊥平面ABC,OG,OF 平面ABC,
∴OD⊥OG,OD⊥OF.
以O为坐标原点,OG,OF,OD所在直线分别为x轴,y轴,z轴建立空间直角坐标系,如图,
则O(0,0,0),A(0,-3,0),B),
所以,0,0),
由,得D(0,0,3λ),
则λ).
设平面ABD的一个法向量为m=(x1,y1,z1),
则
令y1=λ,得x1=-3λ,z1=-1,则m=(-3λ,λ,-1).
设平面BCD的一个法向量为n=(x2,y2,z2),
则
令y2=6λ,得x2=0,z2=3,则n=(0,6λ,3).
所以|cos
所以λ=,
所以D(0,0,2),n=(0,4,3),
易知M,
所以,
所以点M到平面BCD的距离d=.
3.解析 (1)证明:过点P作PE⊥AB于点E,
因为平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,PE 平面PAB,
所以PE⊥平面ABC,
又因为BC 平面ABC,所以PE⊥BC,
又PA⊥BC,PE∩PA=P,PE,PA 平面PAB,
所以BC⊥平面PAB,
又AB 平面PAB,所以AB⊥BC.
(2)设AB=2a,BC=2b,由AB⊥BC,得AB2+BC2=AC2,即4a2+4b2=16,所以a2+b2=4,所以b=,
易知PE=,
所以VP-ABC=a(4-a2),
令f(a)=a(4-a2),则f '(a)=(4-3a2),
令f '(a)=0,解得a=,
当0
当
以B为原点,BC,BA所在直线分别为x轴,y轴,过点B且垂直于平面ABC的直线为z轴,建立空间直角坐标系,如图所示,
设BD=m,m>0,则D(m,0,0),C,
所以,
设平面CPA的一个法向量为n1=(x1,y1,z1),
则
令y1=,得x1=1,z1=1,则n1=(1,,1),
设平面PAD的一个法向量为n2=(x2,y2,z2),
则
令y2=,得x2=,z2=1,则n2=,
设二面角C-PA-D的平面角为θ,
则cos θ=
4.解析 因为四边形ABCD为平行四边形,AB=AC=1,AD=,所以AB2+AC2=AD2=BC2,所以AB⊥AC,
因为PA⊥平面ABCD,AB,AC 平面ABCD,所以PA⊥AB,PA⊥AC,
以A为坐标原点,建立如图所示的空间直角坐标系A-xyz.
(1)易得P(0,0,1),B(1,0,0),C(0,1,0),M,
所以,
设平面PBC的一个法向量为n=(x1,y1,z1),
则
令x1=1,得y1=1,z1=1,则n=(1,1,1),
设直线MN与平面PBC所成的角为θ,
则sin θ=|cos<,n>|=,
所以直线MN与平面PBC所成角的正弦值为.
(2)设PA=h(h>0),则A(0,0,0),P(0,0,h),B(1,0,0),C(0,1,0),所以=(0,1,0),
设平面PBC的一个法向量为m=(x2,y2,z2),
则
令x2=h,得y2=h,z2=1,则m=(h,h,1),
易得平面ABCD的一个法向量n0=(0,0,1),
设直线AC与平面PBC所成的角为α,
则sin α=|cos<,m>|=,
即0<,解得0
因为0
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
